致密气井Arps产量递减指数变化特征

梁倚维，王 东,2，李霆钧，杜 超

(1.长庆油田公司 苏里格南作业分公司，陕西 西安 710018； 2.西南石油大学 石油与天然气工程学院，四川 成都 610500；3.长庆油田公司 第四采气厂，陕西 西安 710018)

梁倚维,王东,李霆钧,等.致密气井Arps产量递减指数变化特征[J].西安石油大学学报(自然科学版),2018,33(2):77-81.

LIANG Yiwei,WANG Dong,LI Tingjun,et al.Study on variation characteristic of Arps decline exponent of tight reservoir gas well[J].Journal of Xi'an Shiyou University (Natural Science Edition),2018,33(2):77-81.

引　言

致密气等非常规资源约占总资源量的2/3以上，相对于常规气难于开发利用[1]。实现经济有效开发致密气首先需要保证致密气井一定的初期产量和可采储量，因此致密气井产量预测及可采储量评价正确与否至关重要。在油气井产量预测及可采储量评价方面Arps产量递减规律[2]应用广泛，文献[3-9]给出了递减类型判断、递减参数求取方法，以及产量递减规律模型和产量递减规律的实际应用分析，重点研究了致密气井早期递减指数大于1的情况，分析致密气井在不同渗流阶段递减指数的变化规律。

致密气具有低孔、低渗、低压、低产能、低控制储量特征，其早期产量相对较高，递减快，长时间处于瞬态流动阶段；而后期产量相对较低，递减减缓，长期处于低产水平。应用Arps产量递减规律分析致密气井初期渗流阶段产量时，普遍存在递减指数大于1的情况(常规递减指数为0～1)，这是由于不适合Arps递减规律一个重要条件[10]：渗流处于边界控制流动阶段。应用Arps递减规律进行致密气井早期产量递减数据分析，必须掌握递减指数在不同渗流阶段的变化情况。本文首先对致密气井渗流阶段进行了划分，其次研究Arps递减规律在致密气井产量递减全过程中各个渗流阶段的递减指数变化特征。

1　Arps递减指数b

1945年，Arps基于损失比的定义和取值特征得到3种常用产量递减规律，仅需确定方程中3个参数(初始递减产量qi、递减指数b和初始递减率Di)即可预测未来产量q和累计产量Q(表1)。对于Arps

表1　Arps产量递减方程Tab.1　Arps yield decline equations

递减规律，确定b值至关重要，b值决定递减类型并控制递减曲线的曲率。递减指数b的推导过程如下：

递减率定义

(1)

双曲递减规律

q=qi(1+bDit)-1/b

(2)

对时间求导，得

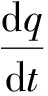
=-qiDi(1+bDit)(-1/b-1)；

(3)

将式(2)、(3)代入式(1)，得

(4)

式(4)倒数对时间求导，得

(5)

从式(4)可以看出，递减率是初始递减率、递减指数和时间的函数，递减率倒数与时间呈直线关系，斜率为递减指数。式(5)显示递减率倒数对时间的导数是递减指数,可据此计算递减指数。

2　致密气井渗流特征

据试井理论的渗流特征[11]，致密气井基本完整的渗流流动阶段可以划分为井筒储集流动、线性流动、拟径向流动、地层线性流动、边界控制流动5个主要渗流阶段和各个渗流阶段之间的过渡流动阶段。由于调查半径公式只适用于径向渗流阶段，并不完全适用于致密气井5个主要渗流阶段，因此如何确定各个渗流阶段的起始时间和结束时间成为解决致密气井问题的难点。本文基于苏X区块63口致密气井产量不稳定方法生产动态历史拟合参数和该区域试井解释认识，建立致密气井数值模型，通过数值试井模拟确定致密气井各个渗流阶段响应时间。

2.1　致密气井数值模型的建立

基于苏X区块63口致密气井生产动态历史拟合参数和该区域试井解释参数的平均值建立致密气井数值模型(图1)，该区域参数的平均值为：孔隙度(体积加权)8.36%，含气饱和度(产层厚度和孔隙度乘积加权)68.2%，产层厚度11.0 m，储层压力33.5 MPa，储层温度110 ℃，井筒储集系数0.4 m3/MPa，表皮系数-4.5，储层渗透率(几何)0.045×10-3μm2，裂缝半长45 m，泄流长度500 m，泄流宽度300 m，泄流长宽比1.67。

图1　致密气井数值模型Fig.1　Numerical model for light gas well

2.2　致密气井渗流阶段的划分

基于上述数值模型，模拟气井定压连续生产5 000 d的产量数据(图2)，采用试井数值模拟方法，依据致密气井5个主要渗流阶段的压力及压力导数双对数曲线特征[12](表2)，划分致密气井各个渗流阶段响应时间。经模拟分析致密气井各个渗流阶段响应时间(表3)，井筒储集流动阶段结束时间

随渗透率或裂缝半长的增加而降低，该流动阶段结束时间都小于0.1 h；随渗透率或裂缝半长增大，线性渗流阶段特征增强，拟径向渗流阶段特征减弱；渗透率和裂缝半长只影响地层线性渗流阶段开始时间，并不影响地层线性渗流阶段结束时间；裂缝半长不影响边界控制渗流阶段开始时间；不同渗流阶段持续时间：线性渗流阶段<拟径向渗流阶段<地层线性渗流阶段。

图2　气井定压生产曲线Fig.2　Constant pressure production curves of gas well

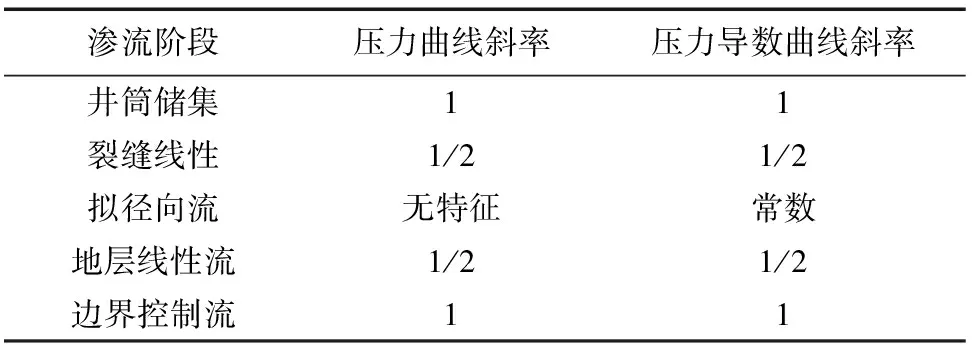
渗流阶段压力曲线斜率压力导数曲线斜率井筒储集11裂缝线性1/21/2拟径向流无特征常数地层线性流1/21/2边界控制流11

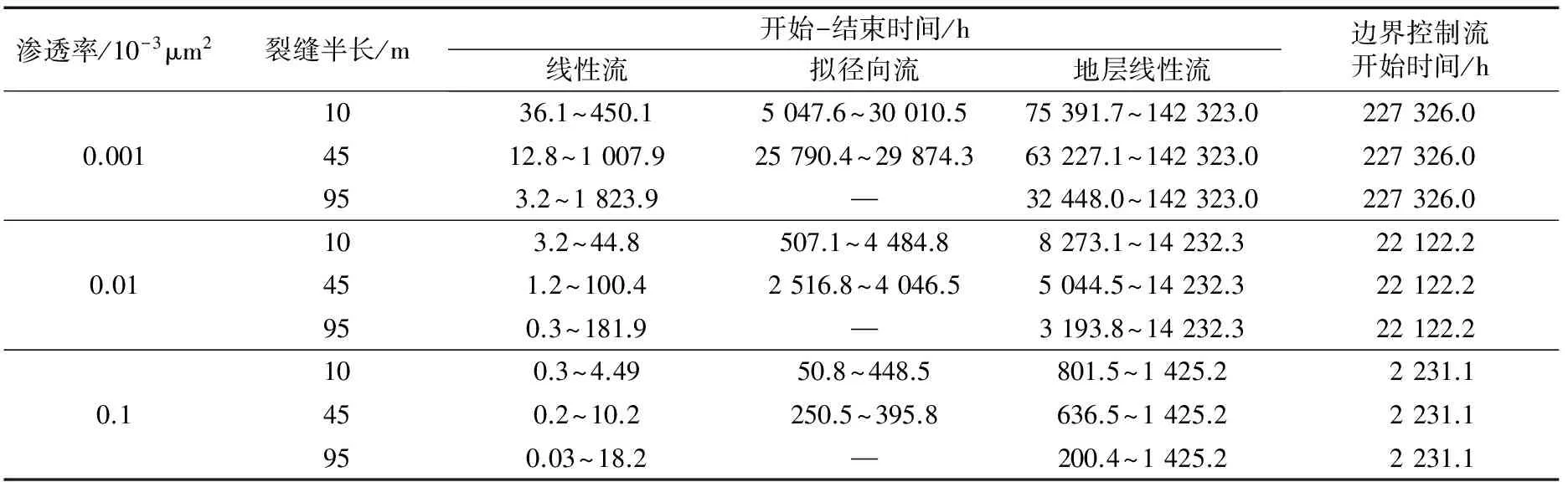
表3　致密气井各个渗流阶段响应时间Tab.3　Response time of different percolation stages in a tight gas well

注：“—”表示拟径向流受裂缝半长影响未反映出压力及压力导数双对数曲线特征。

3　Arps递减指数变化特征

如图3所示，在整个预测期内递减指数变化趋势是先增大后减小,气井的主要流态是地层线性流、地层线性流向边界控制流过渡和边界控制流，裂缝线性流持续时间约4 d，递减指数b=2，随后裂缝线性流向拟径向流过渡约100 d，递减指数增大至峰值4.6，峰值对应时间表示拟径向流的开始，随后渗流依次进入拟径向流约63 d、拟径向流向地层线性流过渡约42 d、地层线性流约383 d、地层线性流向边界控制流过渡约328 d和边界控制流约4 000 d，递减指数呈下降趋势，达到边界控制流后，递减指数b<0.6。

根据以上递减指数变化特征，将气井整个预测期内渗流阶段划分为裂缝线性流(约4 d)、裂缝线性流向拟径向流过渡(4～100 d)、拟径向流向边界控制流过渡和边界控制流4个阶段(图3)。

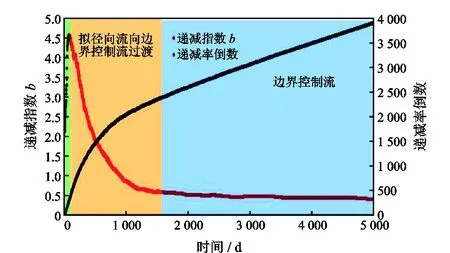
图3　递减指数b随时间变化曲线(渗透率0.01×10-3 μm2,裂缝半长45 m,井底流压5 MPa)Fig.3　Variation of decline index b with time

3.1　渗透率对递减指数的影响

根据图4和表3可知，随渗透率增加，代表径向流开始的递减指数峰值向左偏移，当递减指数b< 0.6时，气井进入边界控制流动阶段，可以判断0.001×10-3μm2的气井处于拟径向流向边界控制流过渡阶段，尚未达到边界控制流阶段，0.01×10-3μm2和0.1×10-3μm2的气井进入边界控制流阶段，0.1×10-3μm2的递减指数小于0.01×10-3μm2的递减指数(图4)。

图4　渗透率对递减指数b的影响(裂缝半长45 m，无限导流裂缝,井底流压5 MPa)Fig.4　Influence of permeability on decline index b variation curve with time

3.2　裂缝半长对递减指数的影响

递减指数随裂缝半长增加而降低，裂缝线性流

阶段递减指数b=2；当裂缝半长150 m时，因无拟径向流响应，渗流直接进入纯地层线性流阶段，递减指数b=2；边界控制流动阶段时，递减指数b<0.6。裂缝半长15 m时，递减指数b近似为0.6；裂缝半长45 m时，递减指数b近似为0.4；裂缝半长150 m时，递减指数b近似为0.3(图5)。

图5　裂缝半长对递减指数b的影响(渗透率0.01×10-3 μm2,无线导流裂缝,井底流压5 MPa)Fig.5　Influence of crack length on decline index b variation curve with time

3.3　有限导流裂缝对递减指数的影响

递减指数随裂缝导流能力增加而降低，有限导流裂缝会形成不同于无限导流裂缝的双线性流，与图5相比，由高导流裂缝形成的无限导流裂缝线性流阶段递减指数b=2，由低导流裂缝形成的有限导流裂缝双线性流阶段递减指数b>2，无因次裂缝导流能力越低，初期递减指数越大,无因次导流能力10与无因次导流能力100的递减指数变化相差不大(图6)。

图6　裂缝导流能力对递减指数b的影响(渗透率0.01×10-3 μm2，裂缝半长45 m,井底流压5 MPa)Fig.6　Influence of crack seepage capacity on decline index b variation curve with time

3.4　不同压降对递减指数影响

递减指数主要差异体现在拟径向流向边界控制流过渡阶段和边界控制流阶段，井底流压高值对应递减指数低值(图7)。

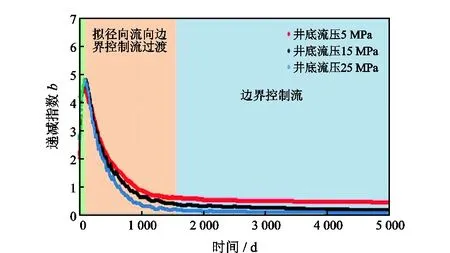
图7　不同压降对递减指数b的影响(渗透率0.01×10-3 μm2，裂缝半长45 m)Fig.7　Influence of pressure drop on decline index b variation curve with time

4　结　论

(1)递减指数变化具有普遍规律即随时间先增大后减小。

(2)根据递减指数变化特征，可以将致密气井渗流分为4个主要阶段：裂缝线性流阶段、裂缝线性流向拟径向流过渡阶段、拟径向流向向边界控制流过渡阶段和边界控制流阶段。

(3)无限导流裂缝线性流递减指数b=2,有限导流裂缝双线性流递减指数b>2；递减指数介于2和峰值之间,代表渗流处于裂缝线性流向拟径向流过渡；递减指数峰值代表拟径向流向边界控制流过渡的开始；递减指数介于峰值和0.6之间，代表渗流处于径向流向边界控制流过渡；递减指数b<0.6且随时间降低，代表渗流进入边界控制流阶段。

参考文献：

[1]HOLDITCH S A.Tight gas sands[J].JPT,2006,56(6):86-93.

[2]ARPS J J.Analysis of decline curves[J].Petroleum Transactions,1945,160(1):228-247.

[3]陈元千,周翠.线性递减类型的建立、对比与应用[J].石油学报,2015,36(8):983-987.

CHEN Yuanqian，ZHOU Cui.Establishment,comparison and application of linear decline type[J].Acta Petrolei Sinica,2015,36(8):983-987.

[4]陈元千,李剑,雷占祥,等.产量递减阶段开发指标的预测方法[J].新疆石油地质,2013,34(5):545-547,496.

CHEN Yuanqian,LI Jian,LEI Zhanxiang，et al.Method of forecaston production index during production decline

phase[J].Xinjiang Petroleum Geology,2013,34(5):545-547,496.

[5]刘占良,王琪,张林,等.苏里格气田东区气井产量递减规律[J].新疆石油地质,2015,36(1):82-85.

LIU Zhanliang,WANG Qi,ZHANG Lin,et al.Laws for gas well production decline in east area of Sulige Gas Field,Ordos Basin[J].Xinjiang Petroleum Geology,2015,36(1):82-85.

[6]王京舰,王一妃,张晗,等.神木气田双3区块气井产量递减规律[J].石油化工应用,2015,34(10):16-20,40.

WANG Jingjian,WANG Yifei,ZHANG Han,et al.Laws for gas well production decline in Shuang3 block of Shenmu gas field[J].Petrochemical Industry Application,2015,34(10):16-20,40.

[7]詹泽东,张岩,段永明,等.非常规气藏产量递减规律与评价研究[J].钻采工艺,2016,39(1):76-78,9.

ZHAN Zedong,ZHANG Yan,DUAN Yongming,et al.Production decline and evaluation research on unconventional gas reserior[J].Drilling and Producing Process,2016,39(1):76-78,9.

[8]齐亚东,王军磊,庞正炼,等.非常规油气井产量递减规律分析新模型[J].中国矿业大学学报,2016,45(4):772-778.

QI Yadong,WANG Junlei,PANG Zhenglian，et al.New model of production decline analysis on unconventional oil and gas well[J].Journal of China University of Mining & Technology,2016,45(4):772-778.

[9]游良容,张建国,袁继明,等.低渗透气田产量递减评价方法研究[J].重庆科技学院学报(自然科学版),2017,19(2):29-32.

YOU Liangrong,ZHANG Jianguo,YUAN Jiming，et al.Research of evaluation method of production decline[J].Science and Technology College of Chongqing,2017,19(2):29-32.

[10] AHMED T.Reservoir Engineering Handbook[M].USA:Gulf Professional Publishing,2006.

[11] EHLIG-ECONOMIDES C A,HEGEMAN P,VIK S.Guidelines simplify well test interpretation[J].Oil and Gas Journal，1994(92):29.

[12] BOURDET D.Well Test Analysis:the Use of Advanced Interpretation Models[M].[s.l.]:Elvsevier Science,2002,6-23.