高分辨率阵列感应测井倾角影响校正研究

仵 杰，郭晨彤，杨 林，成志刚，李国利，王 谦，王钰楠

(1.西安石油大学 光电油气测井与检测教育部重点实验室，陕西 西安 710065；2.中国石油集团 测井有限公司，陕西 西安 710077)

仵杰,郭晨彤,杨林,等.高分辨率阵列感应测井倾角影响校正研究[J].西安石油大学学报(自然科学版),2018,33(2):44-50,57.

WU Jie,GUO Chentong,YANG Lin,et al.Correction of dipping effect on high resolution array induction logging[J].Journal of Xi'an Shiyou University (Natural Science Edition),2018,33(2):44-50,57.

引　言

随着油气勘探的不断深入，大斜度、构造高倾角地层井的数量与日俱增。当地层倾角大于30°时，测井响应倾角影响逐渐增大，影响电阻率测井解释的准确性。许多学者研究了感应测井中的倾角影响信号处理校正方法。Howell[1]首先提出将反褶积的方法用于感应测井倾斜影响校正。Sheng[2]利用电磁理论推导出了斜井几何因子解析式，应用于高分辨率阵列感应测井(HDIL)[3]的倾角影响校正，设计体积和电荷影响校正滤波器，但其电荷影响校正十分复杂，很难有效用于实际测井数据校正。肖加奇等[4-5]通过阶跃模型响应数值差分提取体积和电荷影响几何因子，设计体积和电荷影响滤波器，但测井数据处理时需要估计模型，正演配合实现倾角影响校正，过程复杂，处理速度慢。本文将针对阵列感应(MIT)提出的体积解析几何因子和数值电荷几何因子相结合的倾角影响校正新方法[6]应用于高分辨率阵列感应测井(HDIL)的倾角校正中，研究滤波器设计和测井数据处理算法，通过计算机模拟仿真验证研究成果的有效性。

1　斜井几何因子特性分析

感应测井相对于其他测井方法的最大不同在于可以用几何因子来近似描述仪器的响应函数，为测井数据信号处理方法提供了理论基础。当仪器与地层有一定夹角时，直井中的几何因子不再适用，必须提出新的几何因子。目前有两种几何因子，一种是利用电磁场理论推导出的解析几何因子，另一种是利用阶跃模型差分法提取的数值几何因子。

1.1　解析体积几何因子与数值体积几何因子比较

Sheng等[2]提出的解析体积几何因子是基于扰动理论的Born近似，其全空间积分乘以地层电导率不等于均匀地层的视电导率。本文基于直井Gianzero几何因子推导出斜井Gianzero几何因子式

(1)

(2)

式(1)和(2)中

(3)

(4)

式(1)和(2)分别对应全空间的解析体积几何因子和解析电荷几何因子，其中L为发射线圈与接收线圈的距离；k为电磁波传播的波数，φ为方位角；RT、RR为发射、接收线圈到地层环(ρ,z)之间的距离；zT、zR为发射、接收线圈的纵向坐标。数值几何因子的提取方法见文献[4]。图1给出了高分辨率阵列感应测井(HDIL)的7个阵列，倾角60°时，对ρ和φ积分后的解析体积几何因子与数值体积几何因子。计算数值几何因子的阶跃地层电导率为0.1 S/m和0.01 S/m。

从图1知，两种几何因子的形态一致，但幅值不同，解析和数值几何因子的最大峰的数值分别为2.60 S/m和2.25 S/m。数值几何因子是通过模型测井响应提取的，受模型对比度的影响，实际地层可能出现任意对比度，很难用于测井信号处理，而解析几何因子仅与背景电导率有关，可以用直井方法实现信号处理。因此体积影响信号处理中，本文选择解析体积几何因子。

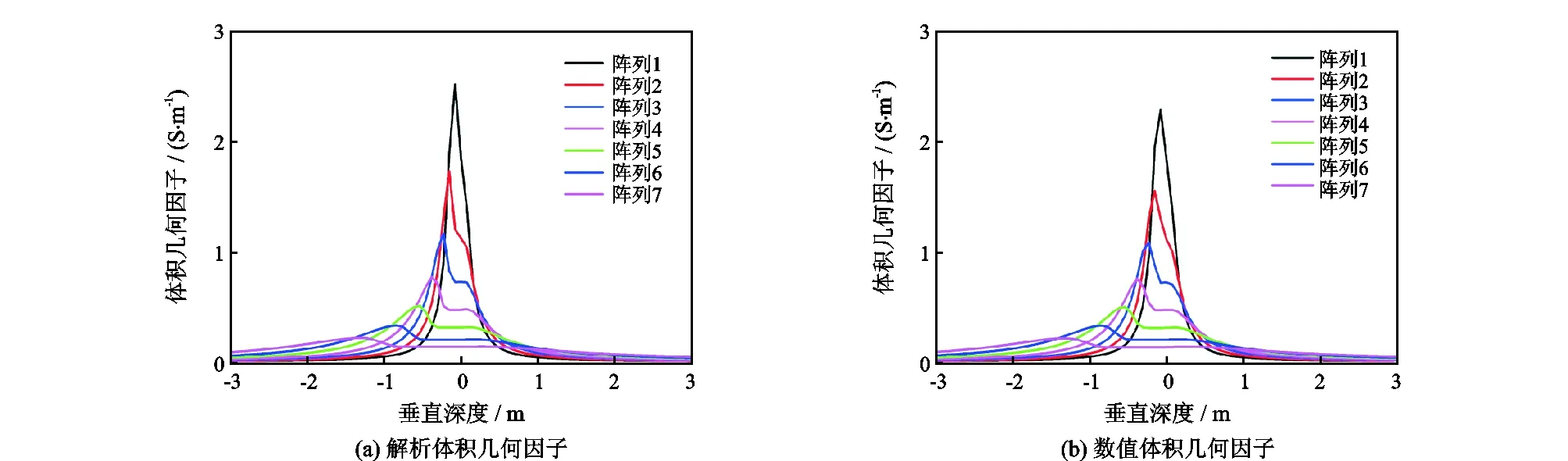
图1　斜井体积几何因子(倾角60°)Fig.1　Volume geometric factors of dip (60°)

1.2　解析电荷几何因子和数值电荷几何因子的比较

图2是60°倾角时的解析与数值电荷几何因子比较。图2中的数值电荷几何因子有2个，分别由上升和下降阶跃模型提取。

从图2知，解析与数值电荷几何因子差别很大。解析电荷几何因子仅与背景电导率有关，不能体现地层边界电荷堆积的特征，实际使用时要估计表征电荷堆积的函数[2]。数值几何因子是从阶跃上升和下降模型测井响应中通过差分提取纵向几何因子，然后适当运算得到的[3]，准确反映了地层边界附近的电荷堆积对7个子阵列的影响特征。上升数值电荷几何因子与下降数值电荷几何因子完全对称，反映电荷堆积的现象。因此本文选择数值几何因子研究去除电荷影响的信号处理方法。

图2　解析与数值电荷几何因子比较(倾角60°)Fig.2　Comparison of analytical charge geometric factors with numerical charge geometric factors (60°)

1.3　对比度对电荷几何因子的影响

数值电荷几何因子反映界面的电荷堆积影响，是否受电导率和对比度的影响？如果不知道影响规律，很难用于实际斜井测量信号处理。下面分析阶跃模型电导率和对比度的影响特征。

1.3.1对比度固定而电导率改变对数值电荷几何因子的影响取阶跃模型电导率对比度为10，选取不同电导率计算分析电导率变化对数值电荷几何因子的影响特征，分别记为低电导率阶跃模型(0.1/0.01)和高电导率阶跃模型(1.0/0.1)。图3给出了2种阶跃模型对应下经过趋肤效应校正后的最短子阵列1和最长子阵列7的数值电荷几何因子响应特征。

从图3知，子阵列1的两条数值电荷几何因子几乎完全重合，说明其不受电导率变化的影响；子阵列7的数值电荷几何因子，中间基本重合，两边有微小差别，电导率大时几何因子的旁瓣减小。图3说明对比度不变时，可以忽略电导率变化对数值电荷几何因子的影响。

图3　相同电导率对比度下的电荷几何因子Fig.3　Charge geometric factors with the same conductivity contrast

1.3.2电导率对比度变化对数值电荷几何因子的影响取3种电导率对比度：5(0.05/0.01)、10(0.1/0.01)和100(0.1/0.001)，提取数值电荷几何因子，如图4所示。

总体看，3种对比度曲线特征趋势相同，对比度越大电荷几何因子数值越大。仔细比较，子阵列1仅在层界面有点差别，离开层界面差别快速减小；子阵列7在发射与屏蔽之间几乎不变，其余位置有点分离。下面的电荷滤波器设计中取对比度为10对应的数值电荷几何因子。

图4　不同电导率对比度下的电荷几何因子Fig.4　Charge geometric factors with different conductivity contrast

2　倾角校正方法研究

斜井校正的目的是消除倾角对测井响应的体积和电荷影响，恢复到直井时的测井响应。针对解析和数值几何因子的特点，笔者提出了解析体积几何因子和数值电荷几何因子相结合的斜井校正新方法，并成功应用于中国石油测井集团公司制造的阵列感应测井仪MIT中的斜井校正[6-7]。本文针对以上的分析，研究如何将该方法应用于高分辨率阵列感应测井(HDIL)的倾角影响校正。

2.1　倾角校正信号处理研究

图5　地层信号、斜井测量信号及斜井处理信号的关系Fig.5　Relationship among formation signal,dip measuring signal and dip processing signal

图5中斜井测量信号与斜井处理信号之间的关系可用数学语言描述为

(5)

(6)

(7)

式(7)中，gj(z,σ,θ)为斜井纵向响应函数，同时包含电荷和体积影响。式(7)是设计斜井校正滤波器的基本方程。实际设计时，式(6)表示的电荷和体积滤波器必须分别设计，下面研究电荷滤波器和体积滤波器的设计方法。

2.2　消除电荷影响的滤波器设计方法

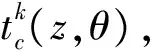
(8)

式(8)是设计电荷滤波器的基本方程。由于上升和下降阶跃模型具有不同的斜井响应函数，求解方程(8)变为同时求解以下2个方程

(9)

(10)

(11)

(12)

2.3　消除体积影响的滤波器设计方法

(13)

(14)

(15)

至此，电荷和体积滤波器设计归结为求解带约束的方程组。实际实现时，可以利用直井中设计聚焦合成真分辨率滤波器的带约束最小二乘最优化方法设计最佳电荷和体积滤波器。

3　倾角校正计算效果分析

设计了高分辨率阵列感应测井(HDIL)中消除倾角影响的电荷和体积滤波器，编程实现斜井测井数据的处理算法，下面通过计算机仿真测试设计滤波器和算法的有效性。

3.1　三层无侵地层

三层模型是测试斜井校正效果最直接和最简单的模型。取三层模型的目的层电阻率为100 Ω·m，上下围岩电阻率为10 Ω·m，层厚4 m，不考虑井眼和侵入影响。图6给出倾角为60°时的校正效果分析。图6(a)为斜井数据直井处理的结果，(b)为先倾角影响校正然后再直井处理结果。为了与直井比较，横向坐标均是垂深。从图6知：

(1)直井处理中(图6(a))，在层界面出现明显尖峰异常；在层中间，不同探测深度曲线分离，表现假“侵入”，10 in读数目的层真值，不受倾角影响，其余曲线受倾角影响，最深影响最大；两侧围岩不同探测深度曲线分离，8 m以后才基本重合。

(2)倾角影响校正后(图6(b))，6条不同探测深度曲线几乎完全重合，与直井处理结果一致，说明倾角影响校正有效消除了倾角的影响。

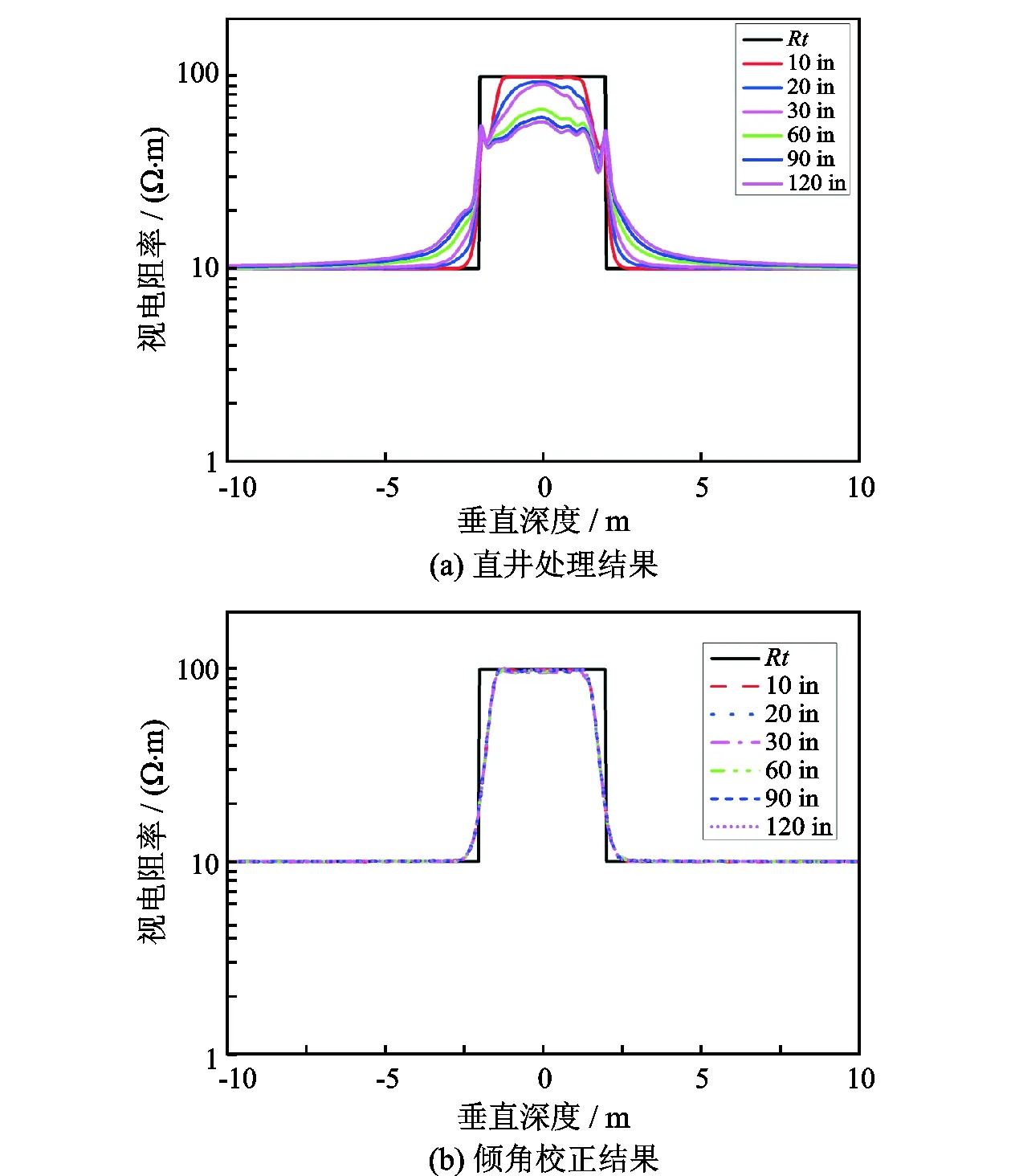
图6　三层地层模拟结果(倾角60°，分辨率0.6 m)Fig.6　Simulation results of three-layer formation (dip angle,60°; resolution,0.6 m)

3.2　十层无侵地层

十层模型测试不同层厚时的倾角影响校正情况。取电阻率对比度为10的十层无侵地层模型，围岩电阻率10 Ω·m，目的层电阻率100 Ω·m，层厚从0.3 m到3 m。图7是倾角为60°时的校正效果分析。与图6类似，横轴为垂深，图7(a)和图7(b)分别为斜井数据直井处理的结果和倾角影响校正后的处理结果。

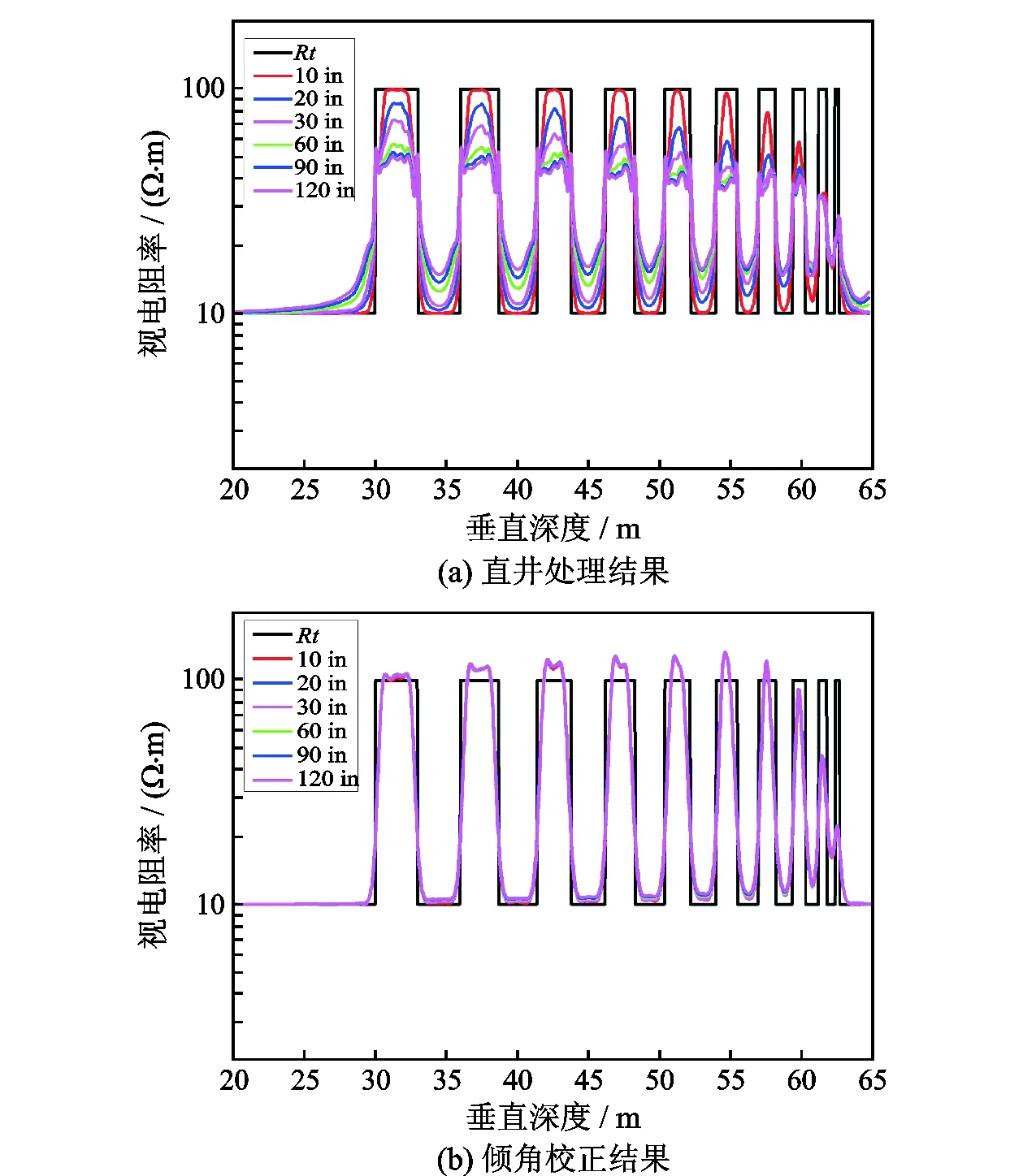
图7　十层地层模拟结果(倾角60°，分辨率0.6 m)Fig.7　Simulation results of ten-layer formation (dip angle,60°; resolution,0.6 m)

从图7知：

(1)直接直井聚焦处理(图7(a))时，不管围岩还是目的层，6条不同探测深度曲线均分离，显示假“侵入”现象；层厚大于1.2 m时，在目的层中，10 in曲线读到地层真值，而90 in和120 in曲线虽然完全分辨层厚，但读数只有50 Ω·m，远偏离真值，围岩部分所有探测深度曲线均分离，受高阻目的层影响严重。

(2)倾角影响校正后(图7(b))，6条不同探测深度曲线几乎完全重合，与直井处理结果一致，层厚0.9 m时近似读到地层真值，层厚1.2～2.7 m，有点过校正。与图7(a)比较，倾角影响明显得到消除。

3.3　Oklahoma地层

Oklahoma地层是一个非常苛刻的多层地层，电阻率从低阻4 Ω·m到高阻1 500 Ω·m，对比度从2到130，层厚从0.6 m到5 m，常用来检测测井信号处理方法的适应性。计算分析了倾角60°和75°两种情况时倾角校正效果，如图8所示。图中同时给出了直接处理结果。从图8知：

(1)直接处理结果中(图8(a)和图8(c))，最浅10 in曲线分辨层厚清楚，其余探测深度曲线随倾角增大分离明显。在深度110 m至115 m的5 m厚地层中，75°时，120 in曲线度数(40 Ω·m) 明显偏离真值(100 Ω·m)。在深度120 m至130 m的10 m厚高阻地层中，60 in至120 in曲线异常。

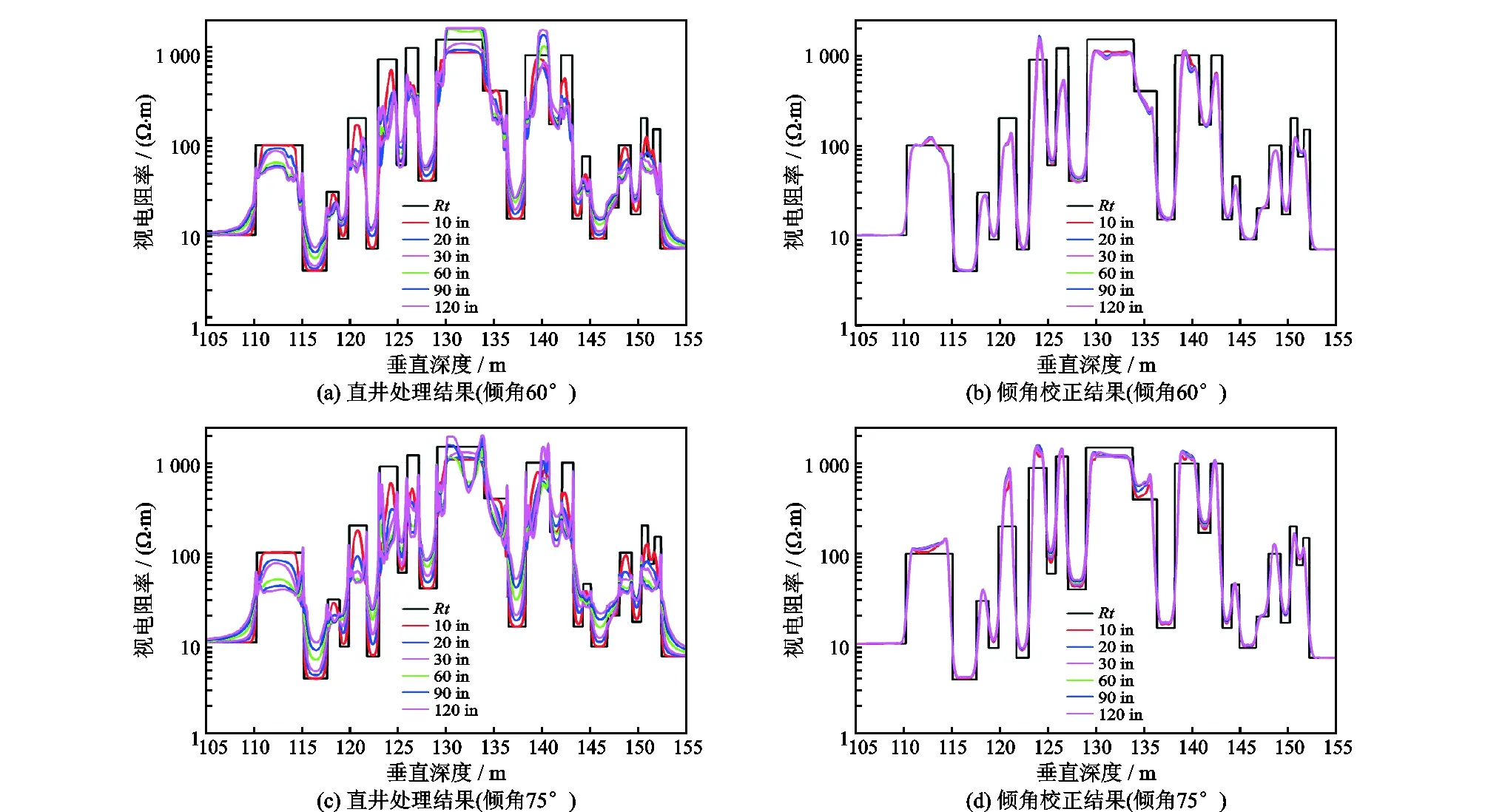
图8　Oklahoma地层模拟结果(分辨率0.6 m)Fig.8　Simulation results of Oklahoma formation (different dip angle,resolution,0.6 m)

(2)经过倾角校正后(图8(b)和图8(d))，与校正前比较，倾角影响明显消除，不同探测深度曲线重合，部分高对比度地层有点过校正，这是由于电荷影响校正使用了固定对比度的数值电荷几何因子。

3.4　基于实际斜井测井数据的建模与校正

图9是某油田(x110-x140 m，地层倾角55°)高分辨率阵列感应测井(HDIL)的实际测井曲线(120 in)及对应的等效地层模型。用正演程序计算测井响应，然后进行直井处理和倾角校正处理，如图10所示。从图10知：

(1)直井处理结果(图10(a))在层交界面两侧和薄层，不同探测深度曲线不重合，出现了假“侵入”现象。

(2)倾角影响校正处理后(图10(b))，不同探测深度曲线重合，层厚分辨清晰，倾角影响完全消除。

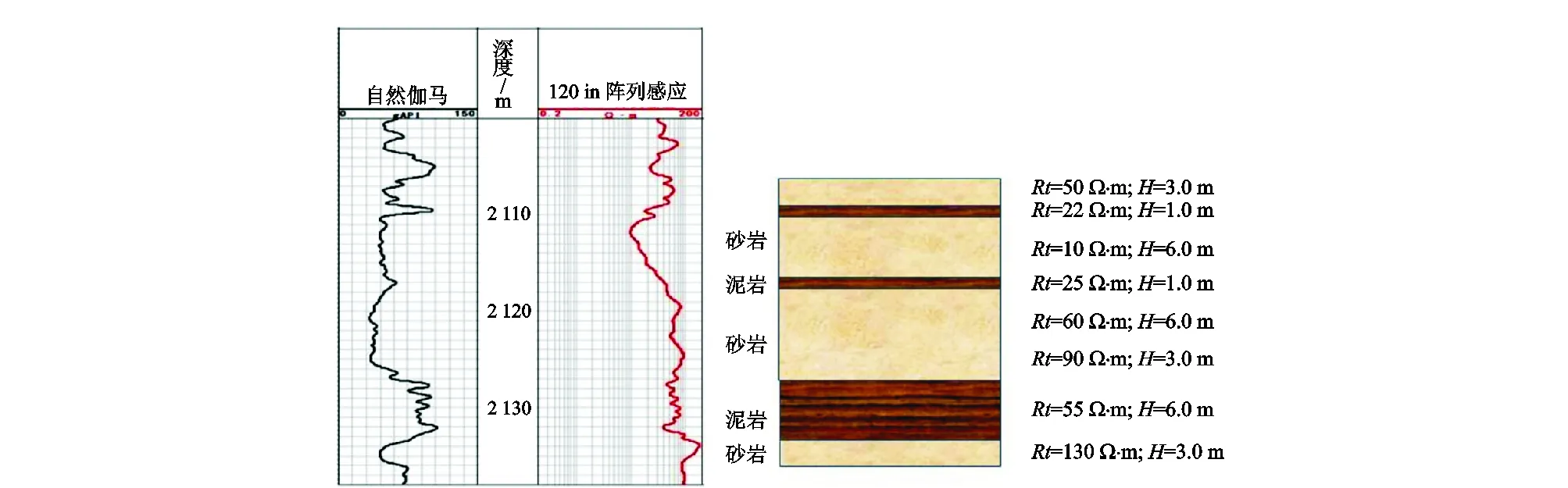
图9　某油田实际测井曲线与模型化图Fig.9　Real logging data and modelling data of an oilfield

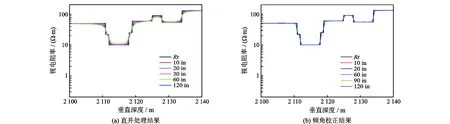
图10　实际测井曲线处理结果(倾角55°)Fig.10　Processing results of a real logging curve(dip angle,60°)

4　结　论

(1)推导出类似直井Gianzero几何因子的斜井Gianzero解析体积和电荷几何因子。通过比较分析趋肤效应校正处理以后的解析斜井几何因子与数值几何因子响应特性，揭示两种几何因子的优缺点。解析斜井体积几何因子仅与背景电导率有关，容易用直井方法设计滤波器，消除斜井体积影响；数值电荷几何因子体现地层边界电荷堆积的特征，解析电荷几何因子不直接反映电荷堆积的现象。同时分析了电导率及其对比度对数值电荷因子的影响规律，为使用数值电荷几何因子消除电荷影响提供理论依据。

(2)针对高分辨率阵列感应测井(HDIL)建立解析体积几何因子和数值电荷几何因子相结合的斜井校正新方法。研究体积影响和电荷影响分离的斜井影响校正方法，推导出设计体积滤波器和电荷滤波器的基本方程及约束条件。

(3)通过无侵三层、十层和Oklahoma地层及某油田实际测井数据模型的计算机仿真数据处理测试并分析了斜井影响校正效果。针对高分辨率阵列感应测井(HDIL)设计的倾角影响校正滤波和测井数据处理算法在倾角小于75°范围可以有效消除测井数据中的倾角影响。

(4)进一步实际斜井测井数据倾角影响校正应用中，还要研究井眼、侵入与倾角影响的关系。

参考文献：

[1] HOWELL E P,FISHER T E.Inducting log deconvolution for deviated boreholes[C]. SPWLA 23th Annual Logging Symposium,orpus Christi,1982.

[2]FANG S,WANG T,GELDMACHER I M.Dipping-effect correction for the high-definition induction logging tool using new geometrical factors[C].Houston :Annual Technical Conference and Exhibition,1999.

[3]张建华,刘振华,仵杰.电法测井原理与应用[M].西安:西北大学出版社,2002:121-127.

[4]XIAO J,BEARD D L,ZHOU Q.A pratical dipping-effect correction for multiarray induction tools in deviated wells[C].SPWLA 37th Annual Logging Symposium,1996.

[5]XIAO J,GELDMACHER I,RABINOVICH M.Deviated-well software focus of multiarray induction measurements[C].SPWLA 41th Annual Logging Symposium,Dallas,2000.

[6]桂彩云.阵列感应测井倾斜校正研究[D].西安：西安石油大学，2011：41-45.

[7]仵杰，桂彩云，解茜草.阵列感应测井斜井信号处理方法研究[J].石油仪器，2011,25(2)：68-70.

WU Jie,GUI Caiyun,XIE Qiancao.A method for processing dipping signals of multiarray induction logs[J].Petroleum Instruments,2011,25(2):68-70.