基于时变T-Copula模型的中国股市国际一体化研究
谈勇贤,郭 颂
(上海财经大学 金融学院,上海 200120)
0 引言
股市一体化作为经济全球化和金融自由化下资本市场的主要发展趋势,其学术研究价值不言而喻。迄今为止,诸多学者分别基于不同的样本和不同的检验方法对全球范围内的股市一体化现象进行了探讨研究。早期的研究主要关注发达国家股市之间的一体化进程,从研究方法来看,早期多数学者考察股市的一体化进程基本都是采用传统的VAR脉冲响应、多元GARCH簇方法以及线性Granger因果检验等分析方法。然而上述研究方法仍然存在一些不足:其一是只能考虑时间序列有限阶滞后影响,通常金融时间序列之间具有复杂的因果关系,伴随着序列非平稳、自相关、异方差以及共线性等影响,而上述检验模型很难实现甄别,以致最后的结论可靠性较差。其二是上述检验方法从本质上来说都是一种线性因果关系检验,经济全球化和金融自由化使得国际金融市场面临结构更复杂的互动关系,金融危机的教训提示应当更加关注股票市场极端价格波动引发的传染效应,显然传统的溢出效应层面的考察并不能有效满足复杂结构下的股票市场一体化进程的研究。其三是上述检验模型通常只能静态地刻画股市联动以及股市传染。
与现有文献相比,本文具有如下特点:一是在一体化研究框架下,分别从联动性与传染性两个方面全面系统地分析了全球范围内的股市一体化程度,形成对现有文献的有益补充。二是分析了以金砖国家为代表的中国市场的股市世界一体化程度,同时基于中国市场系统内部,研究了中国股市与其他金砖国家股市的联动性、传染性,并且从股市传染强度视角,比较了金砖五国股票市场的系统重要性;基于成熟市场系统,对比研究了中国股市的世界一体化程度与成熟市场的世界一体化程度;三是首次基于时变动态Copula技术刻画了股票市场相关结构,并在此基础上,通过Kendall秩相关系数与尾部相关系数分别刻画不同股市之间的联动性与传染性;四是在股市一体化模型构建与实证研究中,充分考虑到不同股市之间的非线性相关结构以及一体化程度的动态变化特征,全面展现不同股市之间相关结构的演化过程。
1 模型构建、样本选取和数据说明
1.1 Copula函数估计相关结构
通常情况下,股票市场价格收益率序列往往存在“波动性集聚”,呈现“尖峰厚尾”的非对称特征,并且多数情况下伴随着“杠杆效应”,传统的分布统计分析不能很好地拟合收益率序列的分布,也不能预测股票价格在极端情形下的变化特征。另外,传统的GARCH模型往往将扰动项设定为正态分布,然而当时间序列存在厚尾状态时,其异常波动情形比在正态分布下更容易发生,这时将扰动项设定为偏t分布可以更精确地刻画价格波动过程。综合考虑,本文对各个股票价格收益率建立ARMA(p,q)-GJRGARCH(1,1,1)-偏t模型以刻画各国指数的边缘分布。模型表达形式如下:
第一个方程为股票收益率的条件均值方程,p和q为其滞后阶数,其最优值通过BIC准则确定;第二个方程表示对股票收益率残差序列εi,t进行标准化处理;第三个方程为股票收益率的条件波动方程,其中wi为常数参数,αi为滞后平方残差项系数,表示未来信息对股票价格的影响程度,βi波动滞后方差项系数,表示波动的记忆性,即上期波动对于当期波动的影响程度。第四个方程为标准化残差序列ei,t服从峰度参数为ηi,偏度参数为λi的偏t分布。
接下来,对各个国家指数边缘分布进行结构Copula函数拟合。根据Copula函数在单调增变化下Copula函数保持不变的性质可知,由于ri,t和rj,t分别是ei,t和ej,t的单调增函数,因此对收益率序列ri,t和rj,t之间相关结构的研究可以转换为对其标准化残差序列ei,t和ej,t之间相关结构的研究。在拟合Copula函数之前,需要对标准化残差序列ei,t和ej,t进行概率积分变换,以得到满足二元Copula函数变量定义域的U(0,1)时间序列,如果经过积分概率变换后的时间序列ui,t和uj,t均服从均匀分布,则可以进行Copula函数拟合估计。考虑到标准化残差序列ei,t和ej,t均服从偏t分布,本文选择椭圆类的T-Copula函数进行结构相关性估计。T-Copula函数本质上是一个结构相关参数为ρ和自由度参数为φ的二元t分布函数,同时,由于Copula函数中的结构相关参数ρ为二元函数分布下的相关性度量,所以可以充分反映各种线性以及非线性相关性信息。
然而上述T-Copula函数的相关结构参数ρ是静态的,不能够反映标准化残差序列ei,t和ej,t(也就是指数收益率序列ri,t和rj,t)的动态变化关系,需要将相关结构参数进行结构性动态演化,基于Manthos Vogiatzoglou(2010)等学者的研究,最能够有效描述T-Copula函数条件相关矩阵的动态过程是DCC过程,所以本文假设相关结构参数ρ的条件相关矩阵服从动态DCC(1,1)过程,从而得到动态时变相关结构参数ρt,具体表达式如下:
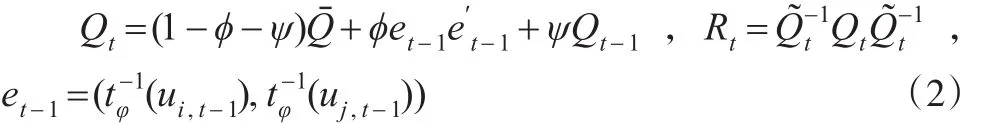
其中,是et的样本协方差矩阵,是主对角元素为Qt平方根,非对角线元素为0的2×2阶矩阵,模型参数约束满足φ+ψ<1;φ,ψ∈(0,1)。
1.2 联动性与传染性的刻画
接下来,本文对股票价格收益率进行联动性效应与传染性效应刻画。联动性的最主要特征是股票价格同步波动的相关性,即ri,t和rj,t同步上涨或者下跌,能够有效描述这一特征的相关性度量被称为一致性度量。经常使用的一致性度量是Kendall秩相关系数τ,其具体定义如下:
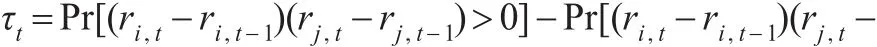

如果表示成Copula函数的形式,则为:
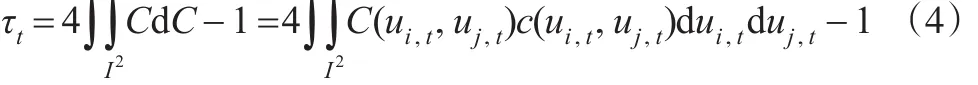
而根据传染性的定义,本文关心的是当某个股票价格异常上涨或下跌(主要是下跌)波动时对于另一个市场股票价格的影响程度,即二者之间的尾部相关性。能够有效描述这一特征的相关性度量被称为尾相关度量。最经常使用的尾相关度量是上下尾相关系数λu和λl,其具体定义如下:
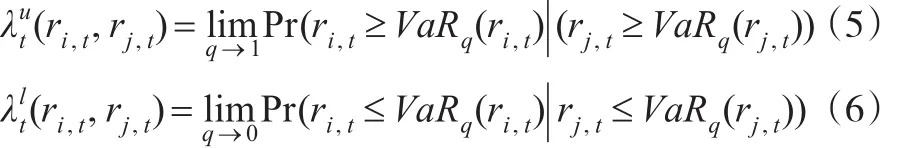
而当Copula函数为时变T-DCC-copula函数时,尾相关度量上下尾相关系数和与时变结构相关系数ρt之间具有如下的关系:
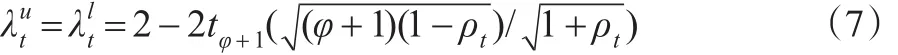
1.3 样本选取与数据说明
成熟市场方面,本文选取老牌资本主义发达国家,主要是德国、法国、英国以及日本。对于世界市场,作为全球最具影响力的股市,美国股市的变化往往左右着其他国家股市的变化,其国际影响甚为重要,毫无疑问是最重要的世界市场。代表性指数选取方面,依次选取中国上证综合指数作为中国股市指数代表;成熟市场方面,选取英国富时100指数、德国法兰克福DAX30指数、法国CAC40指数、日经225指数作为成熟市场指数代表;选取美国S&P500指数作为世界市场指数代表。这些指数也是多数学者的普遍选择,上述各个国家市场指数分别记为:CN(中国)、BR(巴西)、SA(南非)、IN(印度)、RE(俄罗斯)、USA(美国)、GM(德国)、FR(法国)、UK(英国)和JP(日本)。
本文选取的样本期间是从2005年1月4日至2015年11月20日。删除因节假日不同等导致交易日指数缺失的数据,最后得到2093组日数据。指数日收益率通过对日收盘价做一阶对数差分得到,为了减少计算误差,日收益率均乘以100,即rt=100*ln(Pt/Pt-1),其中rt为指数在t日的日收益率,Pt为指数在t日的收盘价,Pt-1为指数在t-1日的收盘价,这样就得到了指数的日收益率序列。
2 实证分析
各个国家市场指数日收益率序列的基本描述性统计如下页表1所示。
由表1可知,在样本考察期内,中国市场整体收益率均值水平均高于成熟市场以及世界市场,而作为世界市场的美国市场收益率平均水平保持在0左右。与之相对应的是中国市场的收益率标准差也要高于成熟市场以及美国市场,这说明中国市场在保持高收益率的同时,其自身风险状态也比较高。所有指数的偏度值均小于0,说明上述指数收益率均呈现后尾状态,而峰度值都超过了4,说明尖峰效应明显。所有指数的JB检验统计量都很显著,说明上述指数序列都不服从标准正态分布,基于传统正态分布的溢出效应检验会导致偏差。Q(10)检验表明,在滞后10阶、10%的显著水平下,除了德国市场指数以外,其他市场指数均具有自相关性,而ARCH效应检验表明,在滞后10阶,1%的显著性水平下,上述指数序列仍然具有明显的条件异方差性,呈现显著的“波动性集聚”状态;ADF单位根检验和KPSS平稳性检验均表明,在1%的显著水平下,上述各个指数都是平稳的。因此,总体来看,所有指数序列都具有尖峰、后尾和条件异方差的特点。
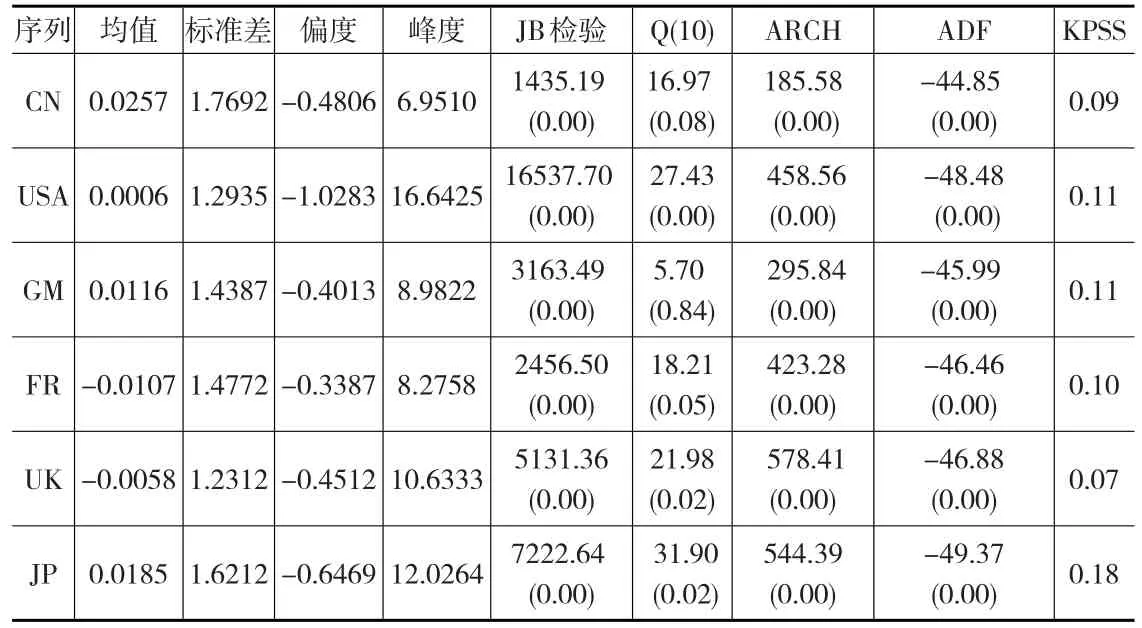
表1 各国指数收益率的统计性描述
考虑到上述特点,接下来本文将使用ARMA(p,q)-GJRGARCH(1,1,1)-偏t模型来模拟上述指数序列的边缘分布,其结果如表2所示。
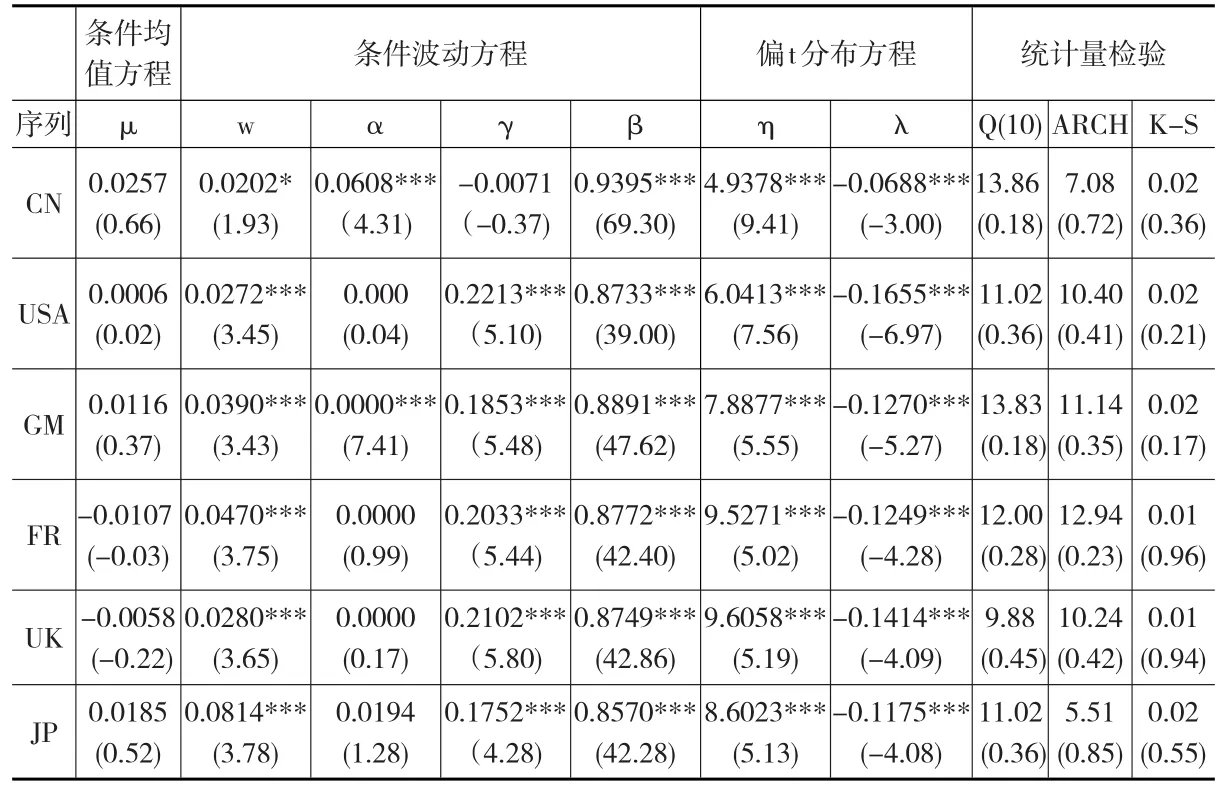
表2 ARMA(p,q)-GJRGARCH(1,1,1)-偏t模型的参数估计结果
由表2可知,在条件均值方程ARMA(p,q)中①本文设定ARMA(p,q)中的最高滞后阶数为5阶,并且依据BIC准则来确定最优滞后阶数,结果发现所有的股票指数序列的最优滞后阶数为:p=0,q=0,即条件均值模型实际上为ARMA(0,0)形式,故参数只有一个μ。,所有股市均值溢出效应均不显著。在条件波动方程GIRGARCH(1,1,1)参数估计结果中,在10%的显著性水平下,常数项w均很显著;对于滞后平方残差项的系数α而言,中国市场指数的系数α在10%的显著性水平下都很显著,而世界市场以及除了德国之外的其他成熟市场的系数α均不显著,这说明中国股票市场当期价格容易受到前期新信息的显著影响,而前期相关信息却不会对成熟股票市场以及世界股票市场当期价格产生显著性影响,成熟股票市场的有效性程度高于中国市场;对于波动滞后方差项的系数β来说,所有市场指数的系数值在1%的显著性水平下都很显著,这说明,无论是中国市场还是成熟市场以及世界市场,股票价格波动都具有记忆性,即前期价格波动会显著影响后期股票价格波动;在偏t分布方程的参数估计结果中,所有股市指数的非对称参数λ和峰度参数η在1%的显著性水平下都很显著,说明所有股市指数序列都具有尖峰和后尾特征,并且呈现有偏状态。Q(10)、ARCH分别是针对标准化残差序列et进行的滞后10阶自相关检验与异方差检验,检验结果表明在5%的显著性水平下,标准化后的残差序列均已无明显自相关与异方差特征。而对标准化残差序列et经过积分变换后的序列ut行K-S分布拟合检验,结果表明在1%的显著性水平下所有序列ut都通过了K-S检验,说明它们均服从U(0,1)分布。综合来看,建立ARMA(p,q)-GJR GARCH(1,1,1)-偏t模型可以很好地对上述股票指数边缘分布进行描述,并且可以发现不同股市价格波动的一些重要信息,从而可以建立时变Copula模型来准确研究不同国家股市之间的相关结构。
3 中国股市与成熟股市的世界一体化差异
下页表3给出了成熟股市市场指数与美国S&P 500指数的T-DCC-Copula函数拟合结果。
由表3可以看出,在10%的显著性水平下,所有二元分布T-Copula函数自由度参数均很显著,说明T-Copula函数可以较好地度量股票指数的相关结构,同时每个相关结构DCC动态演化参数(尤其是第二个参数)显著性很高,说明与中国市场股市相比,成熟股市与世界股市的相关性动态变化特征更加明显,所以时变T-DCC-Copula模型可以有效地刻画成熟股市与世界股市整体相关结构及其动态变化特征。
下页图1给出了包括德国、法国、日本以及英国在内的老牌发达资本主义国家成熟市场与美国市场的动态Kendall系数变化情况,同时为了进行比较研究同时还给出了中国股市与美国股市的动态Kendall系数变化情况。
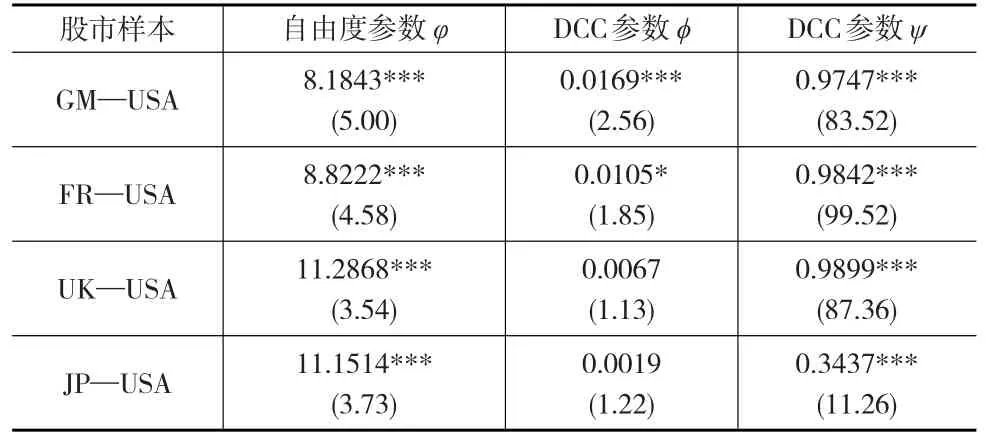
表3 时变Copula模型的参数估计结果
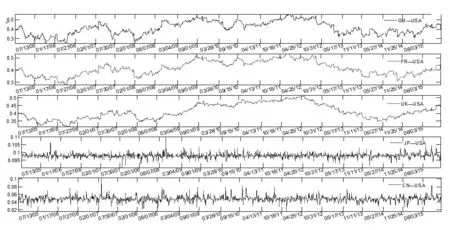
图1 中国股市、成熟股市与世界股市的动态Kendall系数
由图1可以看出,发达国家的成熟市场的世界一体化程度也不尽相同,其中德国、法国以及英国股市与美国股市的动态Kendall系数走势波动情况基本一致,系数平均水平为0.4左右,而波动区间也基本是在[0.3,0.5]上,而日本股市与美国股市的动态Kendall系数走势情况却与上述国家不同,其系数值的平均水平为0.1左右,并且其波动区间也是位于[0.095,0.015]上,整体来看,成熟市场的股市世界一体化程度要普遍高于中国市场的世界一体化程度,依据经济基础假说,这主要与其对外贸易活跃程度有关。
就金融危机以及欧债危机期间的联动性来看,欧洲成熟市场的动态Kendall系数表现基本一致,即在2008年之后,欧洲成熟市场与美国市场的动态Kendall系数逐渐升高,并且在金融危机与欧债危机期间保持较高的联动程度,动态Kendall系数值基本维持在0.5左右,并且波动较小,并且高联动程度的持续时间较长,基本上直到2014年才逐渐下降到正常水平,而后又开始逐渐升高,这说明,在危机期间,成熟市场与世界股市的联系较稳定时期更为密切,并且危机事件对于成熟股市的世界一体化联动性影响时间较长。相比之下,在危机期间,日本市场的动态Kendall系数表现和中国股市有些相同,并没有出现明显的系数变化情况,而是维持之前的平均水平上下波动,说明危机事件对于亚洲股市的世界一体化联动程度影响很低,不过总体来看,日本股市的世界一体化程度仍然高于中国股市。
图2显示了在样本考察期内,发达国家成熟股市与美国股市之间的动态上下尾部系数(或者)走势及其波动情况,即股市传染性的动态变化情况。德国股市与美国股市的动态上下尾部系数(或者)最高,波动区间为[0.1,0.3],平均水平超过了0.2,接下来是法国股市与英国股市,动态上下尾部系数(或者)平均水平大致为0.15,大致也在[0.1,0.3]上波动,而日本股市与美国股市的动态上下尾部系数(或者)却较低,其平均水平大约为0.016,波动区间为[0.0155,0.017],但是仍然高于中国股市以及大部分新兴股市与美国股市的动态上下尾部系数(或者),并且就整体水平来看,与中国市场相比,成熟市场的世界一体化程度较高,同时相互之间的传染性也较高。
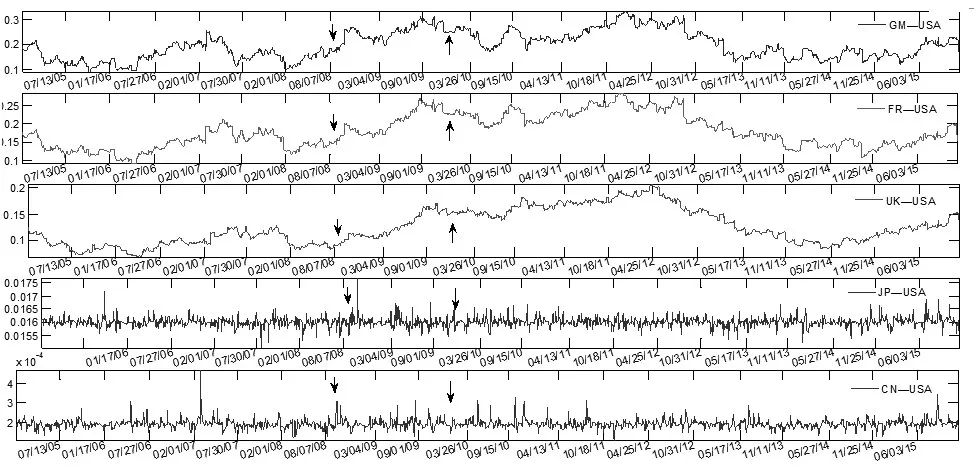
图2 中国股市、成熟股市与美国股市的动态尾部系数
在图2中同样标注了美国金融危机以及欧洲次贷危机发生的时间节点,通过该时间节点前后的动态上下尾部系数(或者λl)走势波动情况,可以窥探危机事件对于成熟股市与世界股市在危机期间的传染性情况。具体来说,2008年金融危机发生后,欧洲成熟股市与世界股市的传染性急剧上升,远远超过正常水平,之后随着欧洲债务危机的发生,由于欧洲成熟市场与债务国之间的政治经济联系程度较高,欧债危机的持续蔓延再次推动传染性逐渐升高,达到样本时间内的最高处,并且一直持续到2012年底左右,才开始逐渐下降,而日本股市与美国股市之间的传染性在金融危机发生后迅速升高,但是又迅速下降,危机事件的冲击效应持续时间很短,而中国股市和美国股市之间的传染性在危机期间波动不大,基本上不明显,所以上述事实说明了随着股市一体化程度的不同,某个国家市场受到金融危机的影响持续时间也不同,当与世界股市的联动性较高时,金融危机的传染持续时间较长,而当联动性程度较低时,受危机影响的程度较低。
因此,成熟股市与世界股市之间的传染性整体水平较高,尤其是在金融危机以及欧债危机期间,传染性不再是某个时间节点的特有现象,而是持续显著的长期性现象。当危机信息蔓延时,成熟市场股市收益率的波动由于在短期内剧烈波动,以此对投资者的心理预期产生影响,使得成熟市场与世界市场的股票价格异常波动,并且由于预期性因素的持续性,这种异常波动产生的传染性也持续显著,所以在股市世界一体化进程中要格外关注传染性。
4 结论及建议
本文基于联动性与传染性的视角,考虑到股市结构的时变与非线性特征,运用动态Copula技术刻画股票市场相关结构,进而通过秩相关系数与尾相关系数度量不同股市间的联动性与传染性,分析了中国股市与世界股市的联动性、传染性,并且对比研究了中国股市的一体化程度与成熟市场的一体化程度。结果表明:就中国市场的世界一体化程度而言,随着中国市场与世界股市联动性的提高,股市间的传染性也在提高,尤其是在金融危机以及欧债危机期间;当前阶段中国股市的世界一体化程度要比中国市场一体化程度要低。无论是联动性还是传染性,成熟市场的世界一体化程度普遍比中国市场尤其是中国股市要高,成熟股市与世界股市的联动性在金融危机期间得到显著提高,同时传染性也得到显著提高,并且持续时间较长,所以随着股市世界一体化程度的提高,股市间的传染并不再是某一时间或时点的特有现象,而是一种持续显著的较长期性现象。
继续推进中国股市国际一体化进程是应对经济全球化以及提升国际影响力的必然途径,而当前中国股市的整体国际一体化程度较低,所以一方面要继续加强同世界市场在金融开放、资本流动等方面的深化合作,逐渐提高我国股市的系统重要性与国际影响力;另一方面要时时关注一体化进程中的风险传染,在股市国际化较低的情况下,股市传染是短期股市价格异常波动的特有现象,所以当下我国股市国际化进程要以稳为主,循序渐进,避免激进式改革可能引发的外界风险渠道传染,而随着股市国际化程度的提高,股市传染将会是较长期的持续性现象,因此长远来看,提高资金配置效率,完善价格发现机制,提高市场有效性才能避免市场主体估计不足或者过度反应,从容应对外界风险冲击。
参考文献:
[1]Dooley M,Hutchison M,Transmission of the U.S.Subprime Crisis to Emerging Markets:Evidence on the Decoupling Recoupling Hypothesis[J].Journal of International Money and Finance,2009,28(8).
[2]Modi A G,Patel B K,Patel N R.The Study on Co-movement of Selected Stock Markets[J].International Research Journal of Finance and Economics,2010,(47).
[3]Aloui R,Alissa M S B,Nguyen D K,Global Financial Crisis,Extreme Interdependences,and Contagion Effects:The Role of Economic Structure?[J].Journal of Banking and Finance,2011,35(1).
[4]Samarakoon P.Stock Market Interdependence,Contagion,and the U.S.Financial Crisis:The Case of Emerging,Frontier Markets[J].Journal of International Financial Markets,Institutions and Money,2011,(21).
[5]马君璐,吴蕾,靳晓婷.美国危机向亚洲中国市场传染过程中的多米诺效应研究[J].世界经济,2012,(6).
[6]何光辉,杨咸月,陈诗一.人世以来中国证券市场动态国际一体化研究[J].经济研究,2012,(10).
[7]赵进文,苏明政,邢天才.未预期收益率,传染性与金融危机——来自上海市场与世界市场的证据[J].经济研究,2013,(4).
[8]王健.中美股市联动性——基于极大重叠离散小波变换的研究[J].世界经济文汇,2014,(2).
[9]梁琪,李政,郝项超.中国股票市场国际化研究:基于信息溢出的视角[J].经济研究,2015,(4).
[10]刘源,邱丽萍,刘涛.ARCH簇模型在股市风险价值测度中的应用[J].特区经济,2017,(1).

