黑龙江省空气负离子浓度空间分布预测

王吉祥，杨江宁，张冬有

空气负离子主要是由空气中的含氧负离子与若干个水分子结合而成的原子团，具有杀灭细菌、清洁除尘、提高免疫力的作用，被人们盛誉为空气中的“维生素”，是综合反映空气质量的一个重要参考标准［1－3］。 1889 年，德国科学家 Elster和 Geital首次发现了空气中存在着负离子，1902年，Aschkinass等肯定了其存在的生物学价值［4，5］，1903 年，苏联科学家发表了空气负离子在疾病治疗中具有积极作用的文章［6］，随后，西方发达国家掀起了对空气负离子研究的热潮。中国的空气负离子研究起源于20世纪70年代末，从最初空气负离子浓度的测定，到其在医疗保健中的作用及机理研究，再到与环境生态的关系研究［7，8］，在30多年的研究中取得了长足的进展。研究表明，空气负离子在自然条件下不断地产生和消亡，但其浓度具有动态平衡的特征并呈现出一定的日变化和年变化规律，浓度高峰值一般出现在9：00～11：00 和 14：00～17：00，季节动态通常以夏季最高，秋季和春季次之，冬季最低［9－11］。 基于此，本文以黑龙江省为研究区，于2016年夏季在全省范围内选取了331处具有代表性的点进行观测研究，观测点高度相对于地面高出0.2～1.7 m，因为这个范围内的浓度最有益于人类健康［12］，运用不同空间插值方法，对全省的空气负离子浓度空间分布情况进行预测，以期为改善城市空气质量、优化城市生态环境和促进城乡规划发展提供可行性参考［13］。

1　区域概况与研究方法

1.1　区域概况

黑龙江省地处中国的东北边疆，地理范围为北纬 43°25′－53°33′，东经 121°11′－135°05′，南北相距约1 120 km，东西相距约930 km，省域总面积约47.3万km2，境内群山连绵起伏，由西北到东南贯穿全省，地处中国地势的第三阶梯，地势西北部、北部和东南部高，东北部和西南部低，森林覆盖率达到43.6%；东北部为三江平原，西部为松嫩平原，是中国重要的商品粮基地。全省大部分地区属于温带、寒温带大陆性气候，四季分明，夏季短暂多雨，冬季漫长寒冷，年平均气温在－5～4℃，年平均降水量在400～600 mm。此外，省内矿产资源丰富，是国家重要的能源工业基地，工业门类齐全，技术水平先进，在中国现代化建设中发挥着重要作用［14］。

1.2　数据来源

空气负离子浓度数据来源于2016年夏季3个月（7月、8月、9月）对黑龙江省的外业观测，一共选取了全省13个地区331个具有代表性的点（图1），观测点所处位置主要包括林地、耕地、居民地、草地、水域、空地等类型。在这3个月内，在天气晴好的情况下，分别对各点的空气负离子浓度进行测量，观测时间为每天 8：00～11：00、14：00～17：00，同时对样点的空气正离子浓度、温度、湿度、光照度进行观测并记录各选取样点坐标以及周围的地理环境特征。

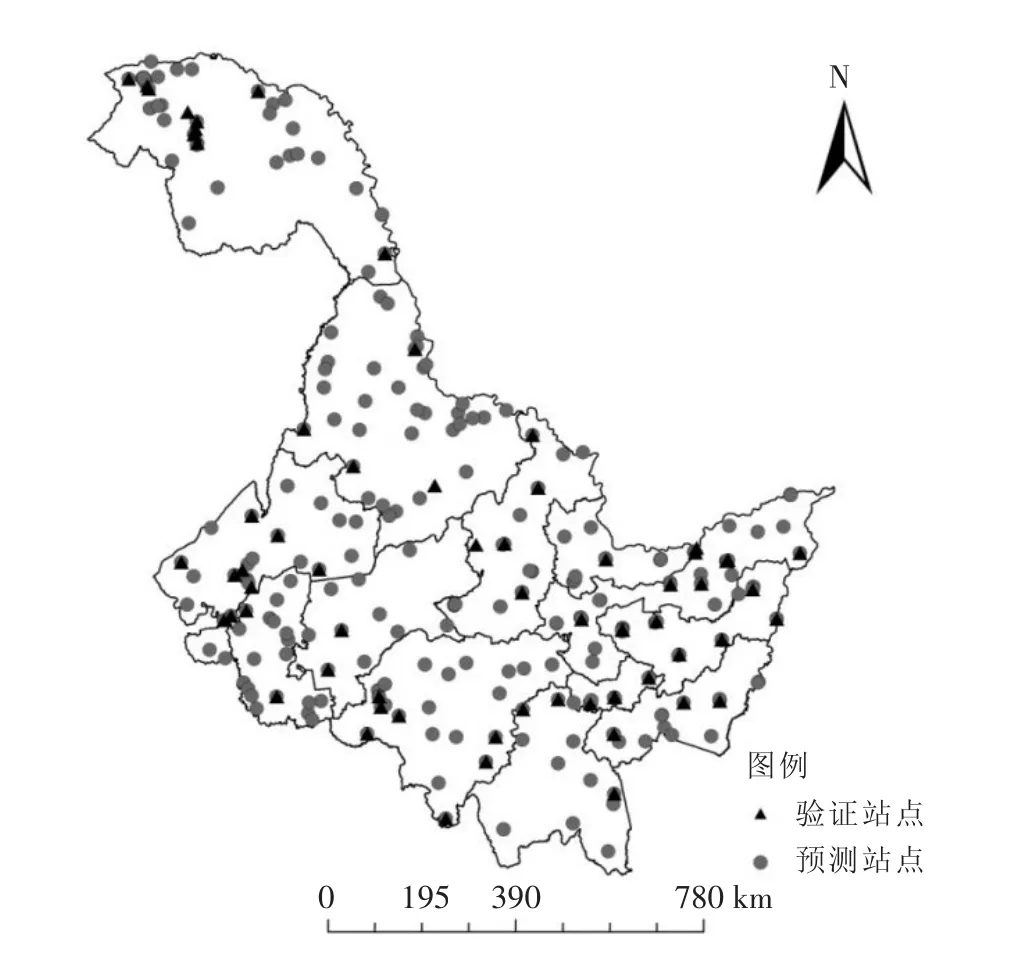
图1　研究区空气负离子浓度观测点分布

1.3　观测仪器

对黑龙江省不同地域的空气负离子浓度观测仪器使用的是日本COM3200PRO林业负离子检测仪，其灵敏度和精度高，且测量内容多样，包括空气正离子、负离子浓度、温度值和湿度值。该仪器的使用原理是采用日本JIS空气中离子密度测定方法中最准确的同轴二重圆筒式构造，每隔2 s读取一个数值，测量误差≤±5%。为了使测量数据更加精确，在测量前首先要对仪器进行正确架设，架设距离为相对于地面0.2～1.7 m的水平高度，其次将仪器连接笔记本电脑，然后将仪器的进风口朝外进行测量。测量时，操作人员与仪器要保持2～3 m以上距离，待示数稳定后，再分别记录空气负离子浓度值，每点观测两次，每次持续观测10 min左右。

1.4　研究方法

1.4.1数据处理方法 采用SPSS19进行数据的描述性统计分析；采用ArcGIS10.1进行空气负离子浓度的空间插值和空间格局分析；采用Origin8.6进行统计分析并对最后插值结果进行验证。

1.4.2空间插值方法 空间插值是通过已知的空间数据对未知空间数据估测的一种方法［15］，它的前提是空间地物具有一定的空间自相关性。在进行插值运算前，首先要对数据进行预处理，即对空气负离子浓度进行空间自相关分析［16－18］。空间自相关是基于Tobler的地理学第一定律 （即所有的地物间都存在联系， 距离越近联系越强［19，20］）， 运用莫兰指数（Moran’s I）来分析空间数据的统计分布规律的一种方法。 Moran’s I指数的取值范围为［－1，1］，当数值接近1时，则说明事物的空间联系强，相关性高，性质相近，当数值接近0时，则说明事物间的联系较弱，相关性低；当数值接近－1时，则说明事物间的空间异质性较大。

1）普通克里金插值法。普通克里金插值法（Ordinary Kriging，OK）是克里金插值法中使用最多的方法，在数据符合正态分布的前提下对区域化变量的线性无偏最优估计。该方法计算公式［21］可表示为：

式中，Z为估算点的数据值；n为插值站点的数目；λi为参与插值的站点对估算站点属性要素的权重系数，其和等于1；Xi为站点位置。

2）反距离加权插值法。反距离加权插值法（Inverse distance weighting，IDW）是一种常用而简单的空间插值方法，它是基于相近相似的原理，即两个物体离的越近，它们的性质就越相似，反之，离的越远则相似性越小。它以插值点与样本点间的距离为权重进行加权平均，离插值点越近的样本点赋予的权重越大［22］。该方法的计算公式如下：

式中，Z 为估算值；Zi为第 i（i＝1，2，3，…，n）个样本点的观测值；Ci是估算点与第i个样本点距离；n为样本数；p为距离的幂，本研究中p取2，即反距离平方插值。IDW插值方法的精度通常随着样本点分布的不均匀程度增加而降低。

3）径向基函数插值法。径向基函数插值法（Radial basis functions，RBF）属于精确插值方法，是用径向基函数来完成逼近实值函数F＝F（x）某点x函数值的方法，其核心是构造一个具有下述形式的逼近函数S（x），跟其他需要复杂处理的插值方法相比，径向基函数插值法适用于对大量点数据进行插值计算［23］。该方法的计算公式如下：

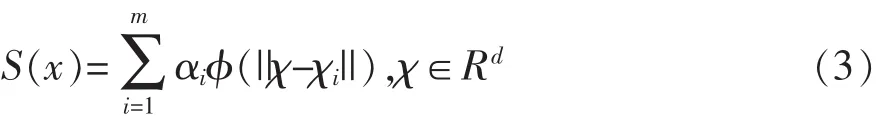
式中，φ（t）（t≥0）是一个确定的实值函数，即径向基函数；｜｜·｜｜表示欧几里得距离；αi和 χi分别为待定系数和径向基函数逼近的节点（i＝1，2，3，…，n）。

1.5　检验方法

在Arc GIS10.1地统计分析中，采用交叉验证的方法来评价不同插值模型的效果，它会每次删除一个数据位置，然后预测关联的数据值并计算不同参数。最优模型通过由平均误差、标准平均值误差、平均标准误差、误差均方根、标准均方根误差来判断，当平均误差绝对值最小，标准平均值最接近于0，误差均方根最接近平均标准误差，标准均方根预测误差最接近于1［24］，模型最优。由于本研究采用的反距离加权插值法和径向基函数插值法只有两组参数结果，为了方便对比，进一步检验不同插值方法在该区域的空气负离子浓度预测精度，在Arc GIS10.1地统计工具下，将331个观测点的平均负离子浓度数据用subset随机构建两个子集，80%的样本（n＝265）为训练要素子集，20%的样本（n＝66）为验证要素子集（图1）。对验证站点的预测值与相同站点的实测值进行相关性分析，从而进一步完成夏季空气负离子浓度不同空间插值方法的精度检验。

2　结果与分析

2.1　空间自相关分析

基于Arc GIS10.1中空间统计模块下的Moran’I指数分析工具，计算得出黑龙江省夏季空气负离子浓度Moran’s I为0.36，说明黑龙江省夏季空气负离子浓度数据具有空间自相关性。

2.2　空气负离子浓度的描述性统计分析

利用SPSS19软件，对空气负离子浓度数据的分布特征进行统计分析，并利用K－S检验对空气负离子浓度进行正态分布检验，若空气负离子浓度不符合正态分布，则需进行log变换或Box－Cox变换进行处理。统计分析结果显示，空气负离子浓度均值（638.638 个 ／cm3）与中值（626.350 个 ／cm3）相接近，偏度为 0.5 接近于 0，峰度为 0.080 接近于 0，K－S 检验值为0.956，检验结果符合正态分布和平稳假设，可以进一步分析其空间结构特征，进行空间插值。

2.3　空气负离子浓度变化全局趋势分析

全局趋势是以空间采样数据为依据来拟合一个数学曲面，通过该曲面来反映数据在空间区域上变化的总体特征。趋势分析图中每一个竖棒表示每个数据点属性值的大小和位置，通过投影将其投射到一个东西向的和一个南北向的正交平面上，每个方向用一个多项式进行拟合，如果拟合曲线为平直的，则说明没有全局趋势；如果拟合曲线为U形线，则说明存在某种全局趋势。确定存在全局趋势后，则可以进行确定性内插插值［25］。

如图2所示，研究区空气负离子浓度基本变化趋势为西高东低，南高北低，南北各点呈现U形变化趋势，表明黑龙江省夏季空气负离子浓度呈现西北－东南高、西南低的空间分布格局。

图2　2016年黑龙江省夏季空气负离子浓度趋势

2.4　变异函数模型拟合

以交叉验证作为评价方法，对普通克里金插值分别采用球面模型、指数模型、高斯模型、环形模型等理论变异函数模型对2016年黑龙江省夏季空气负离子浓度值进行拟合以及采用指数为2的反距离权重插值法和采用样条函数径向基函数插值法进行对比，结果见表2。从表2可以看出，平均误差绝对值中普通克里金插值法＜径向基函数插值法＜反距离加权插值法；误差均方根值为径向基函数插值法＜普通克里金插值法＜反距离加权插值法。在普通克里金插值方法中，平均误差绝对值为指数模型（0.723）＜球面模型（1.307）＜环形模型（1.448）＜高斯模型（1.546），指数模型最小；标准均方根误差值为指数模型（0.869）＞球面模型（0.863）＞高斯模型（0.862）＞环形模型（0.858），指数模型最接近于 1；标准平均值为指数模型（－0.004 1）＞球面模型（－0.005 2）＞环形模型（－0.005 4）＞高斯模型（－0.005 7），指数模型最接近于0；此外，指数模型的误差均方根值和平均标准误差值最接近，所以在普通克里金插值中，空气负离子浓度最佳变异函数模型为指数模型。

表2　研究区空气负离子浓度不同插值方法交叉验证结果

2.5　不同插值方法比较

由于反距离加权插值法和径向基函数插值法只有平均误差和误差均方根两组参数，无法与普通克里金插值进行最优对比，基于此对3种插值方法进行进一步分析，通过对检验站点的空气负离子浓度的实测值（x）与预测值（y）之间的回归关系来确定差值精度较高的模型，结果如图3所示。由图3可知，普通克里金插值选择最优插值模型指数模型，得到方程为 y＝0.932 34x＋60.625 54，R2＝0.840 33（R2为显著性水平检验决定系数，反映因变量的全部变异能通过回归关系被自变量解释的比例）；反距离加权插值法得方程为 y＝0.969 38x＋29.366 35，R2＝0.610 16；径向基函数插值法得到方程为 y＝0.919 85x＋51.763 83，R2＝0.803 96。3种插值方法中基于指数模型的普通克里金插值法的R2最大，其次为径向基函数插值法，反距离加权插值法的R2最小，表明普通克里金插值法的实测值和预测值相关系数最高，其插值方法精度最高，是一种可行的方法。

不同插值方法下的黑龙江省夏季空气负离子浓度分布如图4所示。由图4可知，2016年夏季黑龙江省的空气负离子浓度总体上呈现出由西向东逐渐增高的趋势，同时其分布具有西南低、西北－西南高的特点，一方面因为从西北到西南为绵延广袤的山岭山脉，森林破坏少，空气清新，人类活动较少；另一方面，该省东南部的哈尔滨、大庆和齐齐哈尔为全国重要的工业城市，地处哈大齐工业走廊，经济发达，人口聚集，人类活动活跃，空气负离子浓度值相对较低。

3　小结与讨论

本研究以2016年夏季黑龙江省331观测点的空气负离子浓度数据为基础，在验证其符合正态分布后，进行空间插值，对全省的空气负离子浓度实现了由点到面的空间分布预测。在Arc GIS10.1软件的支持下，将其随机分成两个子集，然后对不同的空间插值结果进行检验。结果表明，2016年夏季黑龙江省的空气负离子浓度存在空间相关性，符合正态分布，所以在进行空间插值时，无需进行数据转换。但是插值的方法有很多，如何选择最优的插值方法仍值得进一步探讨。本研究采用了比较常见的3种空间插值方法，空间插值的结果与预测值均表现出了一定的相关性，其中普通克里金插值的指数模型在空气负离子浓度预测中精度最高，插值结果最优，能够较为准确地反映出2016年黑龙江省夏季的空气负离子浓度空间分布格局。

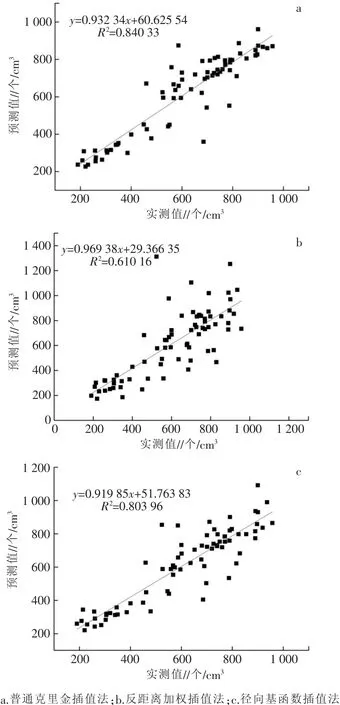
图3　66个检验站点空气负离子浓度实测值与模型预测值的关系

但是本研究中用于插值的空气负离子浓度观测点分布在黑龙江全省，范围较广，虽然综合考虑了不同的土地类型、温湿度、天气状况、高度等因素影响，但从整体上来说，由于林区和无人区原因，布设点分布并不均匀，此外，影响空气负离子浓度空间分布的因素有很多，比如风向、风速、光照度，人类活动等等，因此，针对不同的研究对象，根据研究需要，在进行插值计算时，若想要获取更高的精度，应该充分考虑不同因素对其结果产生的影响，以此获取最优的插值计算。

图4　基于不同插值方法的黑龙江省夏季空气负离子浓度空间分布

参考文献：

［1］黄世成，徐春阳，周嘉陵.城市和森林空气负离子浓度与气象环境关系的通径分析［J］.气象，2012，38（11）：1417－1422.

［2］韦朝领，王敬涛，蒋跃林，等.合肥市不同生态功能区空气负离子浓度分布特征及其与气象因子的关系［J］.应用生态学报，2006，17（11）：3158－3162.

［3］ JOVANI C B R，JOVANI C S B.The effect of high concentration of negative ions in the air on the chlorophyll content in plant leaves［J］.Water， Air and Soil Pollution，2001，129（1－4）：259－265.

［4］章银柯，王 恩，林佳莎，等.城市绿地空气负离子研究进展［J］.山东林业科技，2009，39（3）：139－141.

［5］ KRUEGER A P.The biological effects of air ions［J］.International Journal of Biometeorology，1985，29（3）：205－206.

［6］贺性鹏，李安伯.空气离子对生物体酶的影响［J］.国外医学地理分册，1991，12（2）：57－60.

［7］吴楚材，郑群明，钟林生.森林游憩区空气负离子水平的研究［J］.林业科学，2001（5）：75－81.

［8］ NAKANE H，ASAMI O，YAMADA Y，et al.Effect of negative air ions on computer operation，anxiety and salivary chromogranin A－like immunoreactivity［J］.International Journal of Psychophysiology，2002，46（1）：85－89.

［9］ TAMMET H，HRRAK，LAAKSO L，et al.Factors of air ion balance in a coniferous forest according to measurements in Hyyti，Finland［J］.Atmospheric Chemistry and Physics，2006，6（1）：3377－3390.

［10］石彦军，余树全，郑庆林.6种植物群落夏季空气负离子动态及其与气象因子的关系［J］.浙江林学院学报，2010，27（2）：185－189.

［11］ PAWAR S D，MEENA G S，JADHAV D B.Diurnal and seasonal air ion variability at rural station Ramanandnagar （17°2′N，74°E），India［J］.Aerosol and Air Quality Research，2010，10（2）：154－166.

［12］ TYAGI AK，NIRALA B K，MALIK A，et al.The effect of negative air ion exposure on Escherichia coli and Pseudomonas fluorescens［J］.Journal of Environmental Science and Health.Part A：Toxic／Hazardous Substances and Environmental Engineering，2008，43（7）：694－699.

［13］王 薇.空气负离子浓度分布特征及其与环境因子的关系［J］.生态环境学报，2014，23（6）：979－984.

［14］藏淑英，肖海丰.黑龙江地理［M］.北京：北京师范大学出版社，2014.

［15］蔡迪花，郭 铌，李崇伟.基于DEM的气温插值方法研究［J］.干旱气象，2009，27（1）：10－17，28.

［16］陈彦光.基于Moran统计量的空间自相关理论发展和方法改进［J］.地理研究，2009，28（6）：1449－1463.

［17］ MORAN P A P.Notes on continuous stochastic phenomena［J］.Biometrika，1950，37（1－2）：17－23.

［18］ MORAN P A P.The i nterpretation of s tatistical m aps［J］.Journal of the Royal Statistical Society.Series B：Methodological，1948，10（2）：243－251.

［19］ TOBLER W R.A c omputer m ovie s imulating u rban g rowth in the Detroit Region［J］.Economic Geography，1970，46：234－240.

［20］ T OBLER W.On the first law of geography：A Reply［J］.Annals of the Association of American Geographers，2004，94（2）：304－310

［21］李 新，程国栋，卢 玲.空间插值方法比较［J］.地球科学进展，2000，15（3）：260－265.

［22］朱会义，刘述林，贾绍凤.自然地理要素空间插值的几个问题［J］.地理研究，2004，23（4）：425－432.

［23］魏义坤，杨 威，刘 静.关于径向基函数插值方法及其应用［J］.沈阳大学学报，2008，20（1）：7－9.

［24］李佳珊，张冬有.城市森林公园空气负离子时空分布特征研究［D］.哈尔滨：哈尔滨师范大学，2016.

［25］汤国安，杨 昕.ArcGIS地理信息系统空间分析实验教程［M］.北京：科学出版社，2012.