矩形磁流变弹性薄板的动力稳定性分析

田振国　梁金奎

摘要：磁流变弹性体材料制成的构件在机械荷载和强磁场共同作用下时，材料的弹性模量随外加磁场的变化而变化，构件的变形也使得构件内、外的磁场随之改变，因此这是一个耦合场问题，而且本构关系是非线性的。在载流薄板的运动方程、物理方程及磁流变本构关系的基础上，导出了由磁流变弹性体制成的薄板在电磁场与机械荷载共同作用下的磁弹性动力屈曲方程，应用Galerkin原理将屈曲方程整理为Mathieu方程的标准形式，并将动力屈曲问题归结为对Mathieu方程的求解。利用Mathieu方程解的稳定性，及系数λ和η之间的本征关系，导出了磁流变弹性薄板动力屈曲临界状态的判别方程。讨论了磁场强度、薄板厚度、颗粒体积分数、薄板长度等参量对四边简支磁流变弹性薄板临界失稳荷载的影响。

关键词：动力稳定性；磁流变弹性体；磁弹性；临界失稳荷载；Mathieu方程

中图分类号：0347.2；TB122 文献标志码：A 文章编号：1004-4523（2018）01-0125-07

DOI：10.16385/j.cnki.issn.1004-4523.2018.01.015

引言

磁流变弹性体是通过物理或化学手段，将微米级软磁性颗粒散布在黏塑性态的高分子聚合物基体中，固化后形成的高弹性复合材料。在磁场的作用下，磁流变弹性体内部的颗粒被磁化后，产生相互作用力，并进而影响其弹性模量和阻尼等力学、电学、磁学性能。

目前，对磁流变弹性体的理论研究主要集中在材料制备、力学性能测试以及建立本构关系方面。Dorfmann等分别利用不变量理论及选用应变能函数对磁流变弹性体在平板剪切及圆柱轴向剪切下的力学性能进行了分析。Guan等对磁流变弹性体的磁致伸缩性能进行了研究，结果显示垂直于颗粒链结构方向上的磁致伸缩效应较明显。颗粒体积比越高，磁致伸缩效应越强，多次循環加、卸磁场后会出现残余磁致伸缩效应。杨飏等提出了应用磁流变阻尼装置的顶层隔振控制方法，分析了磁流变阻尼器半主动控制的效果。寇发荣分析了磁流变减振器基本原理和力学模型，开展了磁流变减振器阻尼特性试验和磁流变半主动座椅悬架台架试验研究。黄苗玉等研究了系统在简谐路面作用下随激励频率、激励幅值的分岔特性，并利用相平面图、Poincare截面和功率谱等详细描述了通向混沌振动的路径。赵丹侠等提出一种多级径向流动型磁流变液减振器；建立了磁流变液径向流动控制方程，得出了基于准稳态与非稳态流动的磁流变液减振器阻尼力计算方法。

近年来，磁流变弹性体构件的力学性能引起了人们的关注，梁金奎等分析了磁流变弹性体环形的应力应变在强磁场中的变化规律。朱秘等研究了在不同磁场下磁流变弹性体缓冲装置的缓冲性能，探索了磁流变弹性体在半主动/主动隔振缓冲领域的应用方法。刘子良等设计了以磁流变弹性体作为主要弹性元件的支撑结构，搭建了简谐激励作用下悬臂梁碰撞故障实验系统，研究了系统在不同控制电流下的移频降幅性能，以及碰撞工况下的振动响应。

从目前的研究成果来看，针对于磁流变弹性体本构关系、材料特性及相关的实验研究较多，但对于磁流变弹性体二维构件的稳定性相关理论研究较少。本文研究了磁流变弹性体矩形板的动力稳定性问题，在磁流变弹性体本构关系的基础上，结合磁弹性问题的稳定性方程，得到了由磁流变弹性体制成的薄板在电磁场与机械荷载共同作用下的各向异性的磁弹性动力屈曲方程，应用Galerkin原理将屈曲方程整理为Mathieu方程的标准形式，并将动力屈曲问题归结为对Mathieu方程的求解。利用Mathieu方程解的稳定性，系数λ和η的本征关系，导出了磁流变弹性体薄板动力屈曲临界状态的判别方程，分析了磁感应强度、颗粒体积分数及板的几何尺寸与临界荷载的关系。

1磁流变弹性体薄板的磁弹性动力稳定方程

1.1磁流变弹性体的弹性模量

在偶极子模型中，由磁场引起的磁流变弹性体的剪切模量为

1.2磁流变弹性体薄板的动力稳定方程

由薄板的磁弹性动力稳定性方程

2马丢方程形式动力稳定性方程的建立

若仅考虑通人外部电流的洛伦兹力，而忽略法向磁力作用的情况，将动力稳定性方程（7）整理后可得

对上式进行积分运算，并化简后整理可得

3磁流变弹性薄板磁弹性动力失稳临界状态的判别

式（18）的Mathieu方程是一种周期函数方程。这个方程最重要的性质是当它的系数间满足某种给定的关系时，方程得到无限增长的解。方程的系数λ与η之间的本征值关系是方程稳定解与非稳定解区域的分界。利用Mathieu方程的此种性质可确定磁流变弹性体矩形薄板失稳时临界的状态。方程的本征值关系是一种连分式的表达形式，表达式为

将式（23）和（24）编制成MATLAB计算程序，即可讨论各参量对磁流变弹性薄板的动力稳定性的影响。

4算例分析

薄板问题的屈曲波形是很多个波形的相互叠加，每一种失稳模态形式都有可能存在，但只有最低阶的失稳模态更最具有实际应用意义，因此，下面的计算分析中只给出了四边简支矩形磁流变体薄板最低阶的失稳模态。讨论薄板厚度、颗粒浓度等量变化时，式（16）中的荷载幅值大小P与薄板失稳的关系。

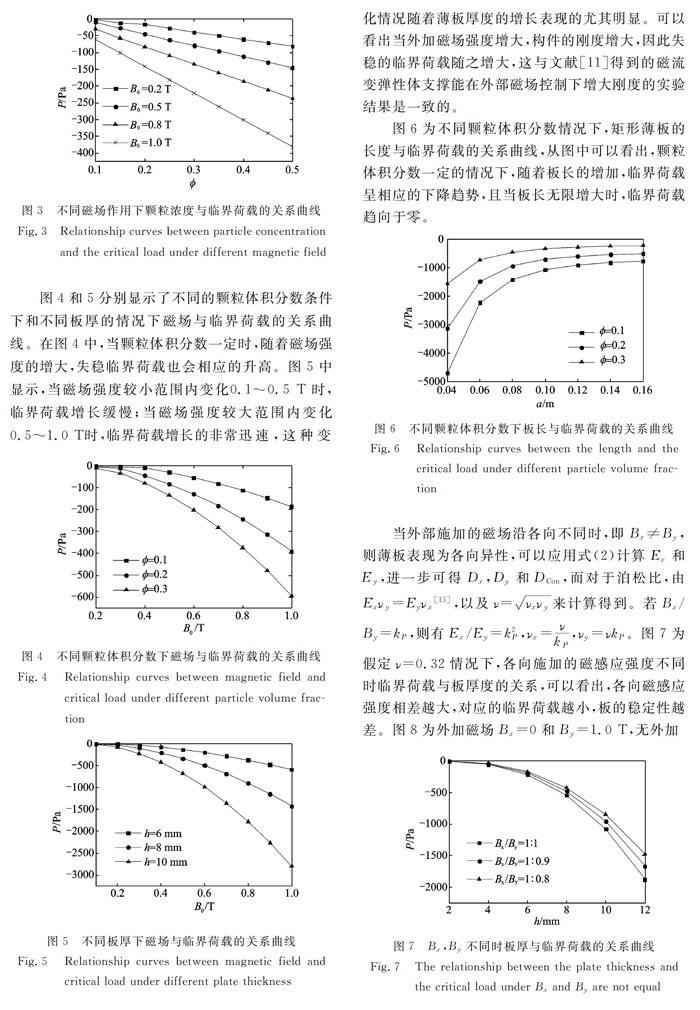
图2讨论了边长为0.1m×0.1m的磁流变弹性体薄板在外加磁感应强度B。不同的情况下，失稳临界状态的荷载幅值大小P随薄板厚度的改变而发生变化。薄板厚度从2mm增长到12ram，相应的失稳临界荷载也随着发生呈抛物线形的增长，而当板厚趋向于零时，临界荷载也趋向于零。并且从此图中还能清楚的看到外加磁场强度对失稳临界荷载的取值有着很重要的影响。当板厚为12mm，B₀=0.2T时，失稳临界荷载为63Pa；但是当B₀=1.0T时，失稳临界荷载却升高到1876Pa，大约是前者的30倍。图3显示了当磁流变弹性体颗粒浓度发生变化时相应的失稳临界荷载相应的改变情况。在磁场强度一定的情况下，随着颗粒体积浓度的增长，失稳临界荷载迅速增大。

图4和5分别显示了不同的颗粒体积分数条件下和不同板厚的情况下磁场与临界荷载的关系曲线。在图4中，当颗粒体积分数一定时，随着磁场强度的增大，失稳临界荷载也会相应的升高。图5中显示，当磁场强度较小范围内变化0.1～0.5T时，临界荷载增长缓慢；当磁场强度较大范围内变化0.5～1.0T时，临界荷载增长的非常迅速，这种变化情况随着薄板厚度的增长表现的尤其明显。可以看出当外加磁场强度增大，构件的刚度增大，因此失稳的临界荷载随之增大，这与文献得到的磁流变弹性体支撑能在外部磁场控制下增大刚度的实验结果是一致的。

图6为不同颗粒体积分数情况下，矩形薄板的长度与临界荷载的关系曲线，从图中可以看出，颗粒体积分数一定的情况下，随着板长的增加，临界荷载呈相应的下降趋势，且当板长无限增大时，临界荷载趋向于零。

当外部施加的磁场沿各向不同时，图8为外加磁场B_x=0和B_y=1.0T，无外加机械载荷情况下，不同板厚时临界电流密度幅值与外加磁感应强度分量B_z的关系曲线。图中可见：板厚越厚，导致矩形板失稳的临界电流密度越大；而在板厚度一定时，随着外加磁感应强度的增加，临界外加电流密度的幅值在减小，这是由于外加磁场引起的洛伦兹力加大，导致临界电流密度的减小。

5结论

磁流变弹性体在工程应用中，除了其材料功能性和结构强度外，还需考虑其动力稳定性。通过本文算例分析可知，磁流变弹性体构件的临界荷载与磁场强度、薄板厚度、颗粒体积分数、构件的几何参量有关。在几何尺寸固定、外加磁场强度一定的情况下，提高颗粒体积分数可以有效提高结构的稳定性。综合来看，颗粒体积分数越高、板厚越厚、板长越小、外加磁场强度越大，构件的稳定性越强。薄板的厚度增加和板长减小使得板的稳定性提高，这是一般材料制成的薄板都具备的性质，而对于外加磁场强度及颗粒体积分数这两个影响因素，是因为磁场强度和颗粒体积分数的提高会使得磁流变弹性体的弹性模量提高，从而提高构件的刚度，进而使得薄板得稳定性提高。