超高结构黏滞阻尼系统风振减振优化设计方法

赵昕　马浩佳　丁鲲

摘要：随着超高结构高度的不断增加，结构的自振频率与强风的卓越频率越来越接近，结构的风振舒适度问题变得愈发显著。黏滞阻尼器是一种无刚度的速度相关型阻尼器，可以有效减小结构在地震作用和风荷载下的振动响应。以反向肘节式黏滞阻尼系统为研究对象，建立了反向肘节式黏滞阻尼系统几何参数优化的数学模型，并提出了反向肘节式黏滞阻尼系统几何参数优化的方法。此外，还提出了一种超高结构黏滞阻尼系统风振减振优化设计方法，该方法可以求得在满足舒适度、阻尼器在50年一遇风下最大功率、中震最大出力约束条件下，黏滞阻尼系统的最优布置位置、数量和阻尼系数。最后以某250m超高层住宅为工程案例，验证提出的超高结构黏滞阻尼系统风振减振优化设计方法的有效性和适用性。

关键词：超高结构；风致振动；黏滞阻尼器；优化设计

中图分类号：TU973.2⁺13 文献标志码：A 文章编号：1004-4523（2018）01-0012-08

DOI：10.16385/j.cnki.issn.1004-4523.2018.01.002

引言

随着超高结构高度的不断增加，超高结构变得更加细柔，结构的自振频率与强风的卓越频率越来越接近，结构的风振舒适度问题变得愈发显著。舒适度性能已经成为超高结构设计的关键设计约束，对于超高层住宅这种具有较高舒适度性能要求的建筑而言，更是如此。

由于超高结构对风荷载比较敏感，因此合理的抗风设计对结构安全性和经济性具有重大的意义。黏滞阻尼器是一种无刚度的速度相关型阻尼器，具有耗能能力强，不提供附加刚度，阻尼力与位移异相位等优点。大量的工程实践证明黏滞阻尼器是一种可以有效吸收和耗散地震作用和风荷载的耗能装置，比如波士顿亨廷顿111大楼、北京银泰中心、天津国贸中心、旧金山四季酒店、波士顿千禧广场等。

然而，由于风荷载作用下结构的层间位移和层间相对速度较小，将黏滞阻尼器应用在刚性结构体系中耗能效果并不太好。肘节式黏滞阻尼系统是一种有效的运动放大装置，可以放大阻尼器在风荷载和地震作用下的变形，从而显著提高阻尼器的耗能效率。

目前，文献中已经有很多关于黏滞阻尼器位置、数量和阻尼系数优化的研究。zhang和soong提出了顺序搜索算法以找到黏弹性阻尼器的最优布置位置和数量。Garcia在此基础上提出了简化的顺序搜索算法以找到线性黏滞阻尼器或者其他线性被动控制装置的最优布置位置和相应的阻尼系数。Lavan和Amir提出了一种基于材料插值技术的黏滞阻尼器型号、布置位置和阻尼系数优化方法。汪大洋和周云采用遗传算法和阻尼控制技术来优化阻尼器的阻尼系数。Lavan和Levy采用割平面法在结构最大位移的约束条件下对框架结构的附加阻尼器进行了优化。Adachi等证明了层间最大相对速度的分布是一个确定黏滞阻尼器分布的关键指标，并提出了一个简化的评估每一层需要的阻尼力的步骤。孙树立等研究了消能减震结构基于响应面法的非线性黏滞阻尼器阻尼系数的优化设计方法。张志强等提出了一个双动力模型来进行带阻尼器结构的风致振动分析，并对阻尼器的阻尼系數进行了优化，使结构的风致响应最小。

目前大多数关于阻尼器位置、数量与参数优化的研究主要解决的是线性黏滞阻尼器在平面框架结构上的布置优化问题，很少能够解决非线性黏滞阻尼器在超高层结构上的布置优化问题。

1肘节式黏滞阻尼系统几何参数优化

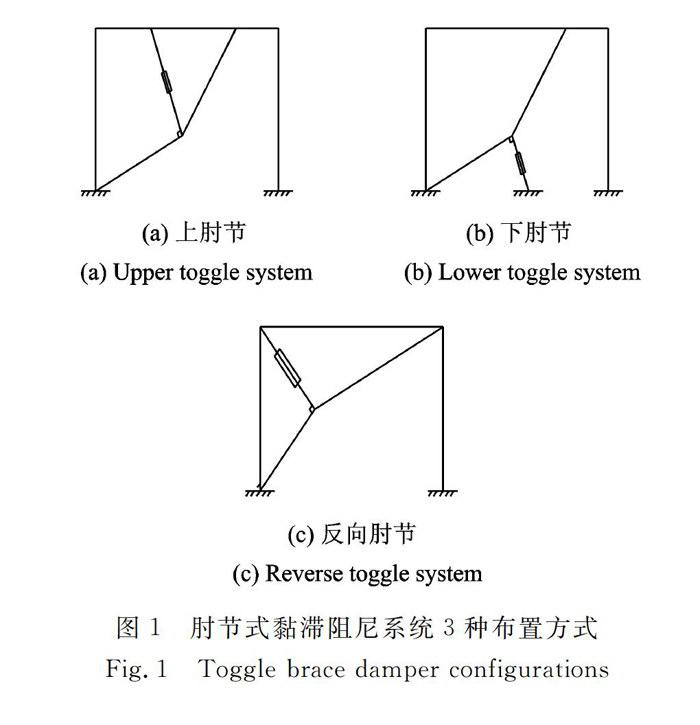
肘节式黏滞阻尼系统根据几何构造的不同，可分为上肘节、下肘节和反向肘节3种布置方式，如图1所示。从图1中可以看出，相对于反向肘节布置方式，上肘节和下肘节布置方式都存在一些缺点。一是为了使位移放大系数取得最大值，阻尼杆需与支撑杆形成90°直角，这样阻尼杆便与楼面梁直接相连。阻尼力将会直接作用于楼面梁上，对楼面梁的设计不利；二是上肘节和下肘节布置方式占据了较多的空间，影响建筑门窗开洞。而反向肘节式的布置方式则不存在这样的缺点，阻尼杆与梁柱节点相连，并且具有足够的空间用于建筑门窗开洞。因此本文将以反向肘节式黏滞阻尼系统为研究对象，介绍其几何参数优化方法。

反向肘节式黏滞阻尼系统的示意图如图2所示。区格的变形主要由弯曲变形和剪切变形两部分组成，其中弯曲变形是由下部的墙柱等竖向构件的轴向变形导致区格发生整体转动而引起的，这部分变形不会引起阻尼器发生相对运动。反向肘节式阻尼器的轴向变形u_D可用位移放大系数f乘以区格剪切变形引起的水平变形u来表示：

（2）式中

u_b为节点b相对于节点d的水平变形；v_a和v_b分别为节点a和b相对于节点d的竖向变形；H和L分别为区格的高度和跨度。

反向肘节式黏滞阻尼系统有3个角度变量θ₁，θ₂，θ₃和3个长度变量l₁，l₂，l₃，只要其中任意两个变量确定之后，反向肘节式装置其他4个变量都可以由几何条件唯一确定。从式（1）可以看出，当θ₁=θ₃时，即l₁⊥l₃，在其他条件相同的情况下，位移放大系数的分子取得最大值。因此，为使反向肘节式黏滞阻尼系统的位移放大作用最大化，应使θ₁=θ₃。这样一旦反向肘节式黏滞阻尼系统的几何参数θ₁确定，其他几何参数也可以确定。此外，当θ₁+θ₂=90°时，位移放大系数取得无穷大值，此时意味着反向肘节式装置成为一个瞬变体系，阻尼器任何微小的变形都会被无限放大而使阻尼器发生破坏。实际的肘节式装置应当是当支撑杆和阻尼杆角度发生微小的变化时，不会引起放大系数产生较大的变化。constantinou等建议在评估肘节式黏滞阻尼系统对角度的敏感性的时候，宜考虑±0.3。的角度变化。为了避免位移放大系数取得过大的值，经过不断试算，本文建议当θ₁变化±0.3°时，位移放大系数的变化量应小于0.2，且位移放大系数不应超过4。

反向肘节式黏滞阻尼系统几何参数优化的数学模型如下列公式所示：

该数学模型中，优化的目标是使位移放大系数f取得最大值，优化变量是几何参数θ₁。式（3b）～（3h）为反向肘节式黏滞阻尼系统几何参数优化的约束条件。其中，式（3b）和（3c）定义了3个角度θ₁，θ₂和θ₃的取值范围为30°～80°。为了满足建筑门窗开洞的需求，θ₂应不小于θ_2min

（4）式中

b为门窗宽度；h为门窗高度。式（3d）～（3f）定义了支撑杆和阻尼杆的长度l₁，l₂和l₃的取值范围；式（3g）和（3h）限制了位移放大系数取过大的值。

由于该优化问题只有一个变量θ₁，因此可采用控制变量法求得使位移放大系数f取最大值的最优几何参数θ₁。优化的步骤为：

（1）提取区格的高度H和跨度L信息；

（2）以0.3°为间隔，使θ₁在30°～80°之间变化，计算每个角度θ₁对应的位移放大系数厂和其他5个变量。

（3）对每个角度θ₁，检查式（3b）～（3h）中约束条件是否满足，找到满足所有约束条件并使位移放大系数f取得最大值的θ₁，即为最优几何参数。

2超高结构黏滞阻尼系统风振减振优化设计方法

当结构高度超过一定高度后，超高结构风振舒适度问题比较严重。本节主要研究如何在结构上布置尽可能少的阻尼器，并使阻尼系数尽可能少，使结构在10年一遇风荷载下顶点加速度峰值满足规范限值。

上述优化问题的优化目标为布置尽可能少的阻尼器，并使阻尼系数尽可能少。优化变量为阻尼器的布置位置、数量和阻尼系数。除了应满足舒适度约束条件外，为防止阻尼器在大震下破坏，还需验算阻尼器在大震下的出力和位移是否超过最大阻尼力和最大冲程。但是中国常规的结构设计是按小震弹性设计，大震弹塑性验算的设计思路来设计的。由于阻尼器在中震弹性下出力与大震弹塑性出力更为接近，本文建议在阻尼器初步设计时控制阻尼器的中震最大出力。优化时阻尼器的中震位移不作控制，最终根据阻尼器在大震下位移确定阻尼器的冲程。为了防止阻尼器在长时间连续工作下由于发热带来的损害，对于主要设计用于抗风的阻尼器，需要对在50年一遇风时程工况下的功率进行严格控制。综上所述，阻尼器优化的约束条件包括舒适度、阻尼器在50年一遇风下最大功率和中震最大出力。

该优化问题具有如下特点：

（1）在阻尼系数相同的情况下，结构顶点X向加速度峰值随X向阻尼器数量增加而单调减小（如图3所示），Y向亦然。因此，在阻尼系数确定的情况下，必存在一个最优的阻尼器数量，使结构顶点加速度峰值接近限值。

（2）当阻尼器数量一定时，随着X向阻尼器阻尼系数增加，结构顶点X向加速度峰值近似线性单调减小（如图4所示），Y向亦然。随着X向阻尼器阻尼系数增加，X向阻尼器在50年一遇风下最大功率近似线性单调增加（如图5所示），X向阻尼器在中震下的最大出力近似线性单调增加（如图6所示）。因此，在阻尼器数量确定的情况下，必存在一个最小的阻尼系数使得结构顶点加速度峰值、阻尼器最大功率、阻尼器最大出力满足限值要求。

基于此，本文采用线性搜索算法来实现在满足结构加速度峰值、阻尼器最大功率、阻尼器最大出力约束下，阻尼器的位置、数量与阻尼系数优化。线性搜索算法是一种比较基本的一维优化算法，其原理是对于一个单变量的连续函数，如果已知两个端点的函数值，通过试探法或插值法构造下一个解，以此方式来缩短迭代区间，最终找到真解。由于线性搜索算法是一维搜索算法，只能解决单变量优化问题，因此将黏滞阻尼器位置、数量和阻尼系数优化分为位置与数量的优化与阻尼系数的优化两个阶段，两个阶段交替进行，并可以相互转化。

在位置与数量优化阶段仅考虑舒适度约束条件，阻尼系数保持不变，采用线性搜索算法求得最优阻尼器数量。其原理为，如果已知当x向和y向阻尼器数量分别为A（k）_x和A（k）_y时，X向和Y向加速度峰值分别为a（m）_x和a（m）_y，当X向和Y向阻尼器数量分别为B（k）_x和B（k）_y时，X向和Y向加速度峰值分别为a（i）_x和a（i）_y，X向和Y向加速度限值分别为[a]_x和[a]_y，则可通过线性插值的方式，估算满足舒适度要求的x向和y向阻尼器数量（如图7所示）：

阻尼器布置应当遵循对称原则，因此需将所有可布位置的阻尼器按照对称性分别沿x向和y向分组。分组的原则是同一区格的2个阻尼器分为一组，关于结构中轴对称的阻尼器分为一组，同组阻尼器同时添加，同时删除。在阻尼器的位置优化时，以10年一遇风荷载时程下每一组阻尼器的平均耗能为指标，按照平均耗能分别对x向和y向的阻尼器组排序。根据耗能排序，依次从B（k）_x个沿x向布置的阻尼器中筛选出不少于λ（k）_x个x向阻尼器，依次从B（k）_y个沿y向布置的阻尼器中筛选出不少于λ（k）_y个y向阻尼器。將筛选的阻尼器布置在结构上，重新计算结构在10年一遇风下加速度峰值，若加速度峰值超过限值，则阻尼器的最优数量落在区间[λ（k），B（k）]；反之落在区间[A（k），λ（k）]。如此阻尼器的最优数量所在区间不断缩小，当阻尼器数量不变时即找到阻尼器的最优数量。

此外，阻尼器布置应使结构在两个方向上的阻尼特性一致，为达到此目的，可使两个方向加速度减振率相等。阻尼器位置与数量优化阶段的数学模型如下列各式所示：

随着优化进行，阻尼器数量保持不变，此时通过调整阻尼系数来满足舒适度、阻尼器最大功率、阻尼器最大出力约束条件，此阶段为阻尼系数优化阶段。如果已知阻尼器数量相同而阻尼系数不同的两个点的加速度峰值、最大功率、阻尼器最大出力，同样可通过线性插值方法确定下一次迭代的阻尼系数。

阻尼系数优化阶段的数学模型为：

（8a）

（8b）

（8c）

（8d）

（8e）式中 F为中震下阻尼器的最大出力，[F]为中震下阻尼器最大出力限值；P为50年一遇风下阻尼器的最大功率，计算方法详见文献；[P]为50年一遇风下阻尼器功率限值。

如果阻尼器最大功率限值或者阻尼器最大出力限值过小，为了满足50年一遇风下阻尼器最大功率或者中震下最大出力约束条件，阻尼系数相对原值减小过多，进而导致加速度峰值超过限值，此时便会从阻尼系数优化阶段重新过渡到阻尼器数量优化阶段，如图8所示。此时按照下式估算阻尼器的数量：

3优化设计流程

超高结构黏滞阻尼系统风振减振优化设计流程为（如图9所示）：

（1）确定黏滞阻尼器可布位置，并将阻尼器分别沿X向和y向分组；

（2）确定黏滞阻尼器的布置方式及相应的几何参数；

（3）计算无控结构在10年一遇风下X向和y向顶点加速度峰值；

（4）计算在初始阻尼系数下，满布阻尼器结构在10年一遇风下的x向和y向加速度峰值、中震下最大出力、50年一遇风下阻尼器最大功率；

（5）按照式（5a）和（5b）估算满足舒适度约束条件需要的X向和Y向阻尼器数量；

（6）根据10年一遇风荷载下每一组阻尼器的平均耗能，对X向和Y向的阻尼器组排序。根据排序结果筛选不少于估算数量的X向和Y向阻尼器；

（7）判断阻尼器数量是否收敛，如果不收敛转步骤（8）；否则采用线性插值方法估算确定下一次迭代的阻尼系数；

（8）判断终止条件是否满足，如果满足，优化结束，否则转步骤（9）；

（9）将筛选的阻尼器布置在结构上，进行时程分析，计算结构在10年一遇风下的X向和Y向顶点加速度峰值、中震下最大出力、50年一遇风下阻尼器最大功率；

（10）按照式（5a），（5b）或（9a），（9b）估算满足舒适度约束条件需要的X向和Y向阻尼器数量，然后转步骤（6）。

4案例研究

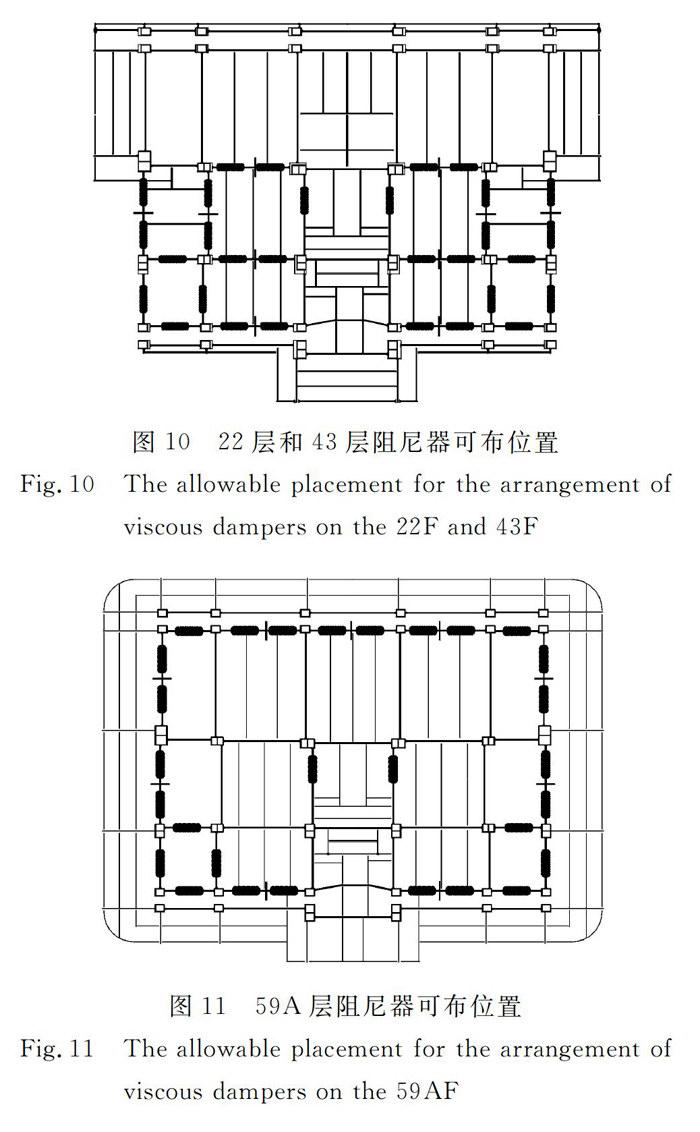
案例选取某245m超高层住宅，地上66层，地下4层，采用钢框架一支撑（剪力墙板）结构体系。结构加强层设置在22层，43层和59A层，22层层高为3.6m，43层和59A层层高为4.38m。由于本项目为超高层豪华住宅，对建筑要求较高，反向肘节式黏滞阻尼器仅允许布置在3个加强层上。22层和43层建筑功能完全相同，其反向肘节式黏滞阻尼器的可布置位置如图10中粗线所示，59A层的反向肘节式黏滞阻尼器可布置位置如图11中粗线所示。全楼共有90个可布位置。

根据风洞试验结果，345°风向角（y主向偏15°）下结构顶点X向加速度响应最大，90°风向角（X主向）下结构顶点Y向加速度响应最大，说明结构横风向加速度响应大于顺风向加速度响应。输入两组风向角下风荷载时程，风荷载持时600s，时间间隔为0.0882s。10年一遇基本风压为0.50kN/m²，50年一遇基本风压为0.80kN/m²。本工程抗震设防烈度为7度（0.15g），设计地震分组为第二组，建筑场地类别为Ⅲ类。输入5组天然地震波和2组人工地震波进行时程分析，地震波波峰值为150gal，双向输入，两个方向的比值为1：0.85。10年一遇风下结构固有阻尼比取1%，50年一遇风和中震下结构固有阻尼比取2%。

阻尼器的阻尼指数取定值0.3，通常在建筑领域采用的黏滞阻尼器设计阻尼力一般不超过2500kN，该吨位下最大阻尼系数为800kN/（mm/s）^0.3，初始阻尼系数取800kN/（mm/s）^0.3。本案例在优化时x向和y向阻尼器的阻尼系数分别进行优化，阻尼系数线性插值间隔为50kN/（mm/s）^0.3。

为了保证黏滞阻尼器在大震下仍能正常工作，大震下与黏滞阻尼器相连的支撑应处于弹性工作状态，其轴力设计值应为消能器在设计速度下对应阻尼力的1.2倍时的轴力，并按轴心受压构件验算其稳定性。本案例阻尼器支撑采用回字形截面，Q345钢材，高度为0.5m，宽度为0.5m，厚度为0.03m。经过验算，采用此截面尺寸，支撑杆在大震下可以保持弹性状态。

结构在10年一遇风下的加速度限值为0.15m/s。，50年一遇风下阻尼器的最大功率限值为2HP，中震下阻尼器的最大出力限值为2800kN（约1.1倍设计阻尼力）。

反向肘节式黏滞阻尼器的几何参数优化结果，如表1所示。

本文采用SAP2000有限元软件的快速非线性（FNA）方法计算结构在风荷载和地震作用响应，并采用MATLAB调用SAP2000API接口的方式实现阻尼器位置、数量和阻尼系数的自动优化。由于风荷载可认为是各态历经性的平稳随机过程，因此采用均方根加速度来评估加速度峰值，计算时选取结构顶部4个角点作为计算点，本案例峰值因子取2.5。经计算，10年一遇风下无控结构顶部X向加速度峰值为0.1333m/s²，y向加速度峰值为0.1876m/s²，y向加速度超过限值0.15m/s²。为满足舒适度要求并使结构在两个方向上的阻尼特性一致，现在结构上布置反向肘节式黏滞阻尼器，使结构顶部y向加速度峰值降至0.15m/s²以下，X向加速度峰值降至0.1066m/s²以下，加速度减振率为20.0%。

经过10次迭代，结构顶部X向加速度峰值降至0.1058m/s²，y向加速度峰值降至0.1491m/s²，满足限值要求。结构顶部X向和Y向加速度峰值迭代图如图12所示，无控结构和有控结构顶部Y向加速度时程对比如图13所示。

优化后X向和Y向阻尼器在50年一遇风下的最大功率分别为0.30HP和0.98HP，X向和Y向阻尼器在7条中震波下平均最大出力分别为486kN和1997kN，所有的约束条件均已满足。最终，X向和Y向各布置4套反向肘节式黏滞阻尼器即可满足要求，阻尼器数量迭代图如图14所示。阻尼器均布置在22层，这是由于结构变形为弯剪型变形，底部以剪切变形为主，阻尼器耗能大。优化后X向和Y向阻尼器的阻尼系数分别为150kN/（mm/s）^0.3。和650kN/（mm/s）^0.3，阻尼系数迭代图如图15所示。由图14和15可知，经过4次迭代，阻尼器数量即收敛，进入阻尼系数优化阶段，后又经过6次迭代，阻尼系数优化完毕，优化结束。

5结论

本文以反向肘节式黏滞阻尼系统为研究对象，建立了反向肘节式黏滞阻尼系统几何参数优化的数学模型，并提出了反向肘节式黏滞阻尼系统几何参数优化的方法。此外，本文还提出了一种基于舒适度性能的超高结构肘节式黏滞阻尼减振系统优化设计方法，该方法可以求得在满足舒适度、阻尼器在50年一遇风下最大功率、中震最大出力约束条件下，肘节式黏滞阻尼器的最优布置位置、数量和阻尼系数。从本文可以得到以下结论：

（1）为了避免位移放大系数取得过大的值，经过不断试算，本文建议当θ₁变化±0.3°时，位移放大系數的变化量应小于0.2，且位移放大系数不应超过4；

（2）案例表明，采用本文提出的几何参数优化方法计算的反向肘节式黏滞阻尼器的位移放大系数在3～4之间；

（3）案例表明，本文提出的黏滞阻尼系统优化设计方法能够解决非线性黏滞阻尼器在超高层结构上的布置优化问题，并且适用于除反向肘节式布置方式外其他的布置方式，唯一的区别在于几何参数的不同。