基于移动质量梁列式的混合编组列车—多跨双线简支梁桥垂向耦合振动分析

文颖　陶蕤　何旭辉　周智辉

摘要：現有车桥振动分析需逐步判断轮对与桥梁单元接触状态，增加了多线混合编组列车与多跨桥梁耦合关系建模的复杂性。基于轮对与桥梁密贴模型，通过引入窗函数，建立轮对与桥梁状态变量的显式关系，推导了移动质量梁动力特性矩阵；将车辆一系簧上部分视为独立多刚体系统，建立了混合编组列车一多跨双线简支梁桥垂向耦合振动分析通用模型。基于Newmark-β法关于状态变量的递推公式，提出了车桥系统方程求解的降阶算法，确保计算规模为最小。开展算例分析，验证了模型的正确性。计算了高速列车一三跨双线简支箱梁桥垂向耦合振动响应，结果表明：车体垂向位移较其他响应在双、单线加载时满足恒定峰值比；桥梁各跨跨中响应最大值在单线行车时基本不变；与单线加载相比，双线对称加载桥跨跨中最大垂向位移近似放大2倍，不对称加载桥跨跨中最大垂向加速度出现下降。

关键词：车-桥耦合；混合编组列车；多跨双线简支梁；移动质量梁；降阶算法

中图分类号：U211.3；U448.13 文献标志码：A 文章编号：1004-4523（2018）01-0001-11

DOI：10.16385/j.cnki.issn.1004-4523.2018.01.001

引言

随着中国高速、重载铁路的快速发展，简支梁桥因架设方便，适应地基不均匀沉降而获得广泛应用。例如，京沪高铁桥线比达到80.5%，双线简支箱梁约占桥梁总长度的88%。朔黄重载铁路预应力混凝土简支梁桥占桥梁总里程的97.57%。与此同时，开行长大列车能降低铁路运营成本而被公认为铁路运输发展的方向。当长大列车经过多跨双线铁路桥梁时，车桥垂向动力相互作用分析需要建立上、下行列车各轮对与各跨桥梁耦合关系，呈现出复杂时变特征。此外，长大列车编组呈现多样性，当调整列车编组后，车桥垂向耦合振动模型随之变化，给应用带来不便。因此，开展混合编组列车一多跨双线简支梁桥系统垂向振动的高效、通用分析方法研究十分必要。

现有车桥垂向耦合振动分析的列式方法主要分为两种：一是将列车与桥梁视为相互作用的整体，采用直接积分法求解系统响应；二是分别建立车辆和桥梁子系统的运动方程，以轮轨位移衔接条件及轮轨力趋向定值作为收敛条件，迭代求解系统响应。它们的共同特点是，每一时间步通过逐一判断各轮对与各桥梁单元是否接触，分别更新车桥系统动力特性矩阵和轮轨力，未建立车桥相互作用通用显式模型。开展混合编组列车一多跨双线铁路桥梁系统垂向振动分析，逐步判断车桥接触状态而修正车桥耦合作用模型是一项复杂而耗时的工作。文献提出了长大列车纵向动力学建模的循环变量方法，解决了传统方法车辆模型通用性差和数据处理效率低的问题，未考虑车桥垂向耦合作用。Yang和Wu提出了车辆一桥梁互制单元，尽管采用动力凝聚技术显著降低求解规模，仍需逐步更新轮对一桥梁耦合关系，当考虑长大列车通过多线桥梁时，不可避免地消耗大量计算资源。此外，更换列车编组后，必须修正计算程序，不便于工程应用。

本文假定列车轮对与桥梁接触。将轮对与桥梁视为整体，基于时间窗函数，给出轮对与桥梁状态变量的关系通式，构造移动质量梁模型。将一系簧上部分（包括车体、转向架和二系悬挂）视为独立多刚体系统（忽略纵向车钩力作用）。基于弹性系统动力学总势能不变值原理，建立了适用于任意编组列车一多跨双线简支梁桥系统垂向振动分析的显式动力特性矩阵，基于Newmark-β法关于速度和加速度的递推公式，提出了车桥耦合大系统运动方程求解的降阶算法。通过与文献结果对比及计算单、双线“先锋号”高速列车经过某三跨简支梁桥时车桥系统动力响应，验证了车桥垂向耦合作用通用模型和求解算法的正确性及适用性。

1车桥系统垂向耦合作用模型

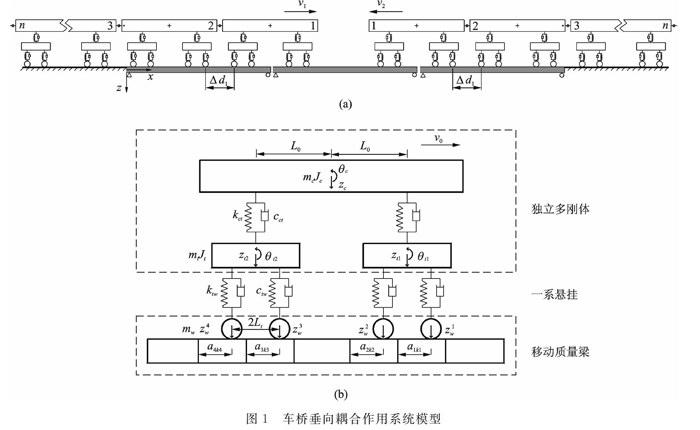
本文考虑混合编组列车与双线铁路多跨简支梁桥的垂向耦合作用（如图1（a）所示），忽略列车横向振动与垂向振动的弱耦合特性（当考虑车桥系统在静平衡位置附近发生垂向线性微振动时，该假定是合理的），主要目的是建立长大列车一多跨双线铁路桥梁系统垂向振动的高效、通用分析方法。

1.1车辆独立多刚体模型

下文选取经典四轴铁路车辆模型为研究对象，本文提出的车桥系统垂向耦合动力学通用分析方法能模拟系列不同类型车辆而无需修改分析程序。假定列车以恒定车速进出桥梁（上、下行线的列车运行速度分别为v₁和v₂），混合编组列车共包含n_v辆车、n_w个轮对，第n辆车与第n+1辆车的相邻轮对间距为△d_n。车辆垂向动力学参数如图1（b）所示，它们的含义是：m_c，J_c和m_t，J_t分别为车体和转向架的质量和面内转动惯量；k_tw，c_tw和k_ct，c_ct为一系和二系悬挂刚度和阻尼常数；m_w为轮对质量。

假定列车轮对与桥梁密贴，轮对自由度不再是独立变量。车辆模型的独立自由度包括车体点头角θ_c和沉浮位移z_c，前、后转向架点头角θ_t1、θ_t2和沉浮位移z_t1，z_t2。因此，图1（b）中车辆一系悬挂以上部分形成了独立多刚体系统。车辆独立多刚体模型的位移向量为

（1）式中各位移分量的正方向如图1（b）所示，n（n=1，2，…，n_v）表示车辆在列车编组中的序号。车辆独立多刚体模型的质量矩阵Mⁿ_v，阻尼矩阵Cⁿ_v和刚度矩阵Kⁿ_v由下式得到

1.2移动质量梁列式

前节已指出列车轮对没有独立自由度，将与桥梁形成相互作用的整体。因此，移动轮对与桥梁构成了“移动质量梁”。移动质量梁的惯性特性来源于梁体均布质量m_b、梁截面转动惯量I_xb和轮对集中质量m_w，剛度与阻尼特性（假定轮对为理想刚体且与桥梁保持完全刚性接触）与原始桥梁一致。为了定量分析移动车轮对“移动质量梁”惯性特性的贡献，必须先确定轮对状态参数（位移、速度及加速度）。当轮对与某桥梁单元接触后，轮对运动状态由运行速度及梁单元节点状态参数唯一确定。

1.2.1轮对一桥梁单元相对位置分析

如前所述，针对混合编组列车一多跨双线桥梁系统垂向振动分析问题，倘若逐步判断所有轮对与桥梁单元的接触状态，将消耗大量计算资源。文献在求解系列移动质量引起的简支梁垂向振动响应时，通过定义窗函数，确定质量单元与简支梁桥的耦合关系。本文借鉴该思路，引入与桥梁单元对应的窗函数，建立描述轮对与桥梁单元接触状态的通用模型。首先引入如图2所示的单位阶跃函数

假定桥梁被划分为n_b个单元，x^k₁和x^k₂表示第k个单元节点局部坐标（以列车进桥端为坐标系原点，列车前进方向为正方向），则l_k=x^k₂-x^k₁为第k个单元的长度。列车进入桥梁的瞬时计为t₀（上、下行线列车进桥时刻分别标记为t^u₀和t^d₀），则第n辆车第h个轮对到达和离开第k个梁单元的时刻分别为：

进入第k个梁单元的时刻

离开第k个梁单元的时刻

1.2.2列车轮对一桥梁运动状态参数显式关系模型

为了突出混合编组列车一双线多跨简支梁桥系统垂向振动分析的通用建模方法研究，忽略轨道结构的传力作用。本节将利用上节得到的轮对与桥梁单元相对位置表达式，建立轮对与桥梁状态参数间的显式关系模型。由于该模型与车辆类型无关，适用于混合编组列车建模。基于轮对一桥梁密贴假定，轮对状态参数满足如下全微分关系

1.3车辆独立多刚体系统一移动质量梁耦合关系列式

本文以车辆一系悬挂为界，将车桥系统处理为车辆独立多刚体一移动质量梁相互作用系统。前两节已分别建立车辆独立多刚体系统和移动质量梁的动力特性矩阵。本节从能量原理出发，推导描述车辆独立多刚体系统一移动质量梁相互作用的动力特性矩阵。一系悬挂内力势能U_s的一阶变分如下

（14）其中与移动质量梁运动状态相关的子矩阵均是时间的显式函数，反映了车辆独立多刚体系统一移动质量梁相互作用的时变特性。

2车桥系统运动方程高效求解的降阶算法

本文采用弹性系统动力学总势能不变值原理和形成矩阵的“对号入座”法则，建立车桥系统运动方程。车桥系统总势能包括前文提到的车辆独立多刚体系统惯性力、弹性力及阻尼力势能U_v、移动质量梁惯性力、弹性力及阻尼力势能U^I_gb+U^e_gb+U^d_gb、一系悬挂内力势能U_s以及反映车辆对桥梁静力加载的车辆重力势能V_v。因此，车桥系统的动力平衡条件为

（15）

（16）将式（2），（11），（14）和（16）代入式（15），可得车桥系统运动方程如下

本文采用Newmark-β法求解式（17）。对于按四轴车辆编组的列车一双线铁路多跨简支梁桥系统，总自由度数为2×n_v×6+3×N-n_c（n_c为桥梁约束自由度数）。随着列车编组数量和桥梁跨数的增加，系统动力特性矩阵阶数将变得异常庞大，严重影响计算效率。为了缩减计算规模，采取分别求解车辆和移动质量梁运动方程的策略。下面以计算车桥系统t+△t时刻动力响应为例进行说明。由New-mark-β法关于计算t+△t时刻速度和加速度的递推公式得

（20）式（19）和（20）都以t+△t时刻车桥系统位移为待求变量，它们构成联立代数方程组。当列车总自由度数多于桥梁总自由度数时（例如，考虑单跨双线铁路桥梁通行长大列车），将式（19）代入式（20），可得求解q^t+△t_b的联立方程组

与式（17）相比，式（21）的待求变量仅剩下桥梁位移，待求变量明显减少。倘若列车总自由度数少于桥梁总自由度数（例如，考虑单辆车通过多跨桥梁），则将式（20）代入式（19），得到以车辆位移q^t+△t_v为全部待求变量的联立方程组，上述降阶算法的目的是确保车桥系统耦合振动分析的待求变量数为最少。

3算例验证

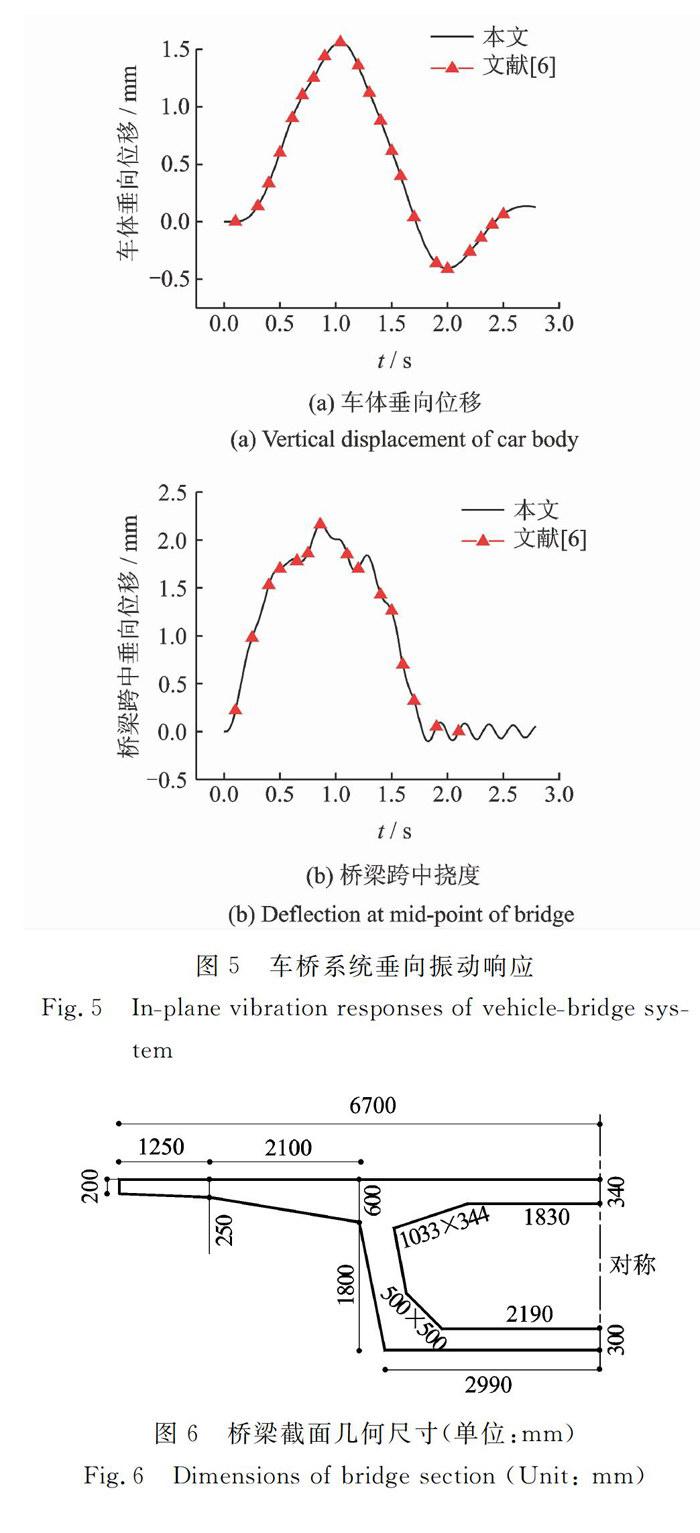
本节选取文献中四轴车辆一单跨简支梁桥系统垂向振动分析算例进行比较说明，车辆和桥梁参数见文献。车体垂向位移和桥梁跨中挠度时程如图5（a）和（b）所示。

当t=1.04s时，车体垂向位移达到最大值1.56mm。桥梁跨中最大挠度及其出现时间分别为2.01mm和t=0.86s，均与文献的结果一致。其他时刻车桥系统动力响应与文献结果吻合良好，从而验证了基于移动质量梁列式的车桥垂向耦合振动分析通用模型及运动方程求解的降阶算法正确性。

4实例分析

本节考虑混合编组列车一双线3跨24m混凝土简支梁桥垂向耦合振动分析。桥梁横截面如图6所示。桥梁混凝土密度ρ_b=2500kg/m³，混凝土弹性模量和剪切模量分别为35GPa和14GPa，桥梁阻尼比取2%。箱梁截面特性参数如表1所示。车辆选取“先锋号”高速列车模型，列车编组为1动+1拖+2动+1拖+1动，车辆模型动力学参数如表2所示。分别计算桥上单线行车（v₁=270km/h）和双线对开（v₁=v₂=270km/h）条件下车桥垂向耦合振动响应。

由图7可知，单线加载时首辆动车和拖车车体垂向位移最大值分别为0.474mm和0.537mm，双线加载时对应的最大值分别为0.782mm和0.888mm，雙、单线行车条件下，动车和拖车车体垂向位移最大值的比值约为1.65且几乎同时达到最大值。由图8和9可知，首辆动车和拖车车体垂向最大加速度在双、单线加载条件下的比值分别为1.79，1.64，最大点头角之比为1.96，1.48。此外，车体垂向峰值位移在双、单线加载时满足一致比例（最大差别在6%以内）。车体垂向加速度和点头角尽管同时达到峰值，但双、单线行车峰值响应比并不维持恒定比例。

由图10不难发现，单线行车条件下各跨桥梁跨中最大垂向位移均稳定在0.828mm，扭转角为3.25×10^-5rad，跨中垂向位移和扭转角时程基本满足一致变化规律，可见列车进入各桥跨的初始状态对桥梁振动响应并无影响。双线对开条件下，各跨跨中最大垂向位移分别为1.34，1.60和1.34mm，是单线加载结果的1.63，1.93和1.63倍。由于第二跨桥梁跨中响应达到极值时，双线列车恰好以跨中对称布置，跨中挠度近似是单线加载结果的2倍，扭转角则趋于零。各跨桥梁跨中最大垂向加速度（如图11所示）在单线加载时保持不变（大致为0.077g），双线对开加载时各跨桥梁跨中最大垂向加速度分别是单线加载结果的0.73，1.84和0.79倍，显见对称加载桥跨跨中最大垂向加速度获得放大，但不满足2倍关系，而不对称加载桥跨跨中最大垂向加速度则下降。

5结论

针对双线混合编组列车一多跨桥梁垂向耦合振动分析通用模型的建立问题，本文通过引入时间窗函数，给出了轮对及桥梁状态变量通用显式表达式，提出了考虑轮对对桥梁移动加载作用的移动质量梁列式。将车辆-系簧上部分视为与列车编组无关的独立多刚体系统，建立了混合编组列车一双线多跨简支梁桥垂向耦合振动分析通用模型，推导了车桥系统显式时变动力特性矩阵，基于Newmark-β法关于相邻时刻速度和加速度的递推公式，提出了车桥系统运动方程求解的降阶算法，以最低计算规模获得车桥系统动力响应。

通过分析文献算例，验证了车桥垂向耦合振动分析的通用模型和求解算法的正确性和适用性。计算了“先锋号”高速列车一三跨双线简支梁桥系统动力响应，结果表明：

1）车体垂向位移在单、双线行车条件下几乎同时达到极值，双、单线加载的峰值响应比按相同规律变化。车体垂向加速度和点头角同时达到峰值，但峰值响应比不同。

2）单线行车条件下，各桥跨跨中动力响应的最大值基本不变且具有相同时程（因列车进桥时间不同，相位有差别），反映出列车进桥状态对桥梁振动影响不大。

3）双线对开条件下，对称加载桥跨跨中最大垂向位移是单线的2倍，跨中扭转角等于零，与静力加载结果一致；对称加载桥跨跨中最大垂向加速度获得放大，但不满足2倍关系，不对称加载桥跨跨中最大垂向加速度则出现下降。