一种求解干摩擦带冠叶片动力学响应的方法
谢方涛 崔璨 马辉 邦椿
摘要:考虑相邻叶冠之间的接触摩擦作用,将扭形带冠叶片简化为自由端带有集中质量的悬臂梁,冠间接触采用带有迟滞特性的宏观滑移模型模拟,基于Timoshenko梁理论和库仑摩擦定理,提出了一种干摩擦扭形带冠叶片动力学响应的数值求解方法。基于所提方法,分析了叶片安装角和扭角对干摩擦叶片动力学特性的影响,并通过有限元方法验证了求解结果。研究结果表明:随着安装角和扭角的增加,会削弱冠间接触表面的减振效果,但并不会对最优法向接触压力产生影响;并且,相比于有限元方法,所提方法在保证求解精度的情况,具有较高的求解效率。此研究结果能够为旋转扭形叶片冠间阻尼结构的设计和优化提供理论指导。
关键词:干摩擦阻尼;带冠叶片;安装角;黏滞-滑动运动
中图分类号:TH113;0322 文献标志码:A 文章编号:1004-4523(2018)01-0110-08
DOI:10.16385/j.cnki.issn.1004-4523.2018.01.013
引言
叶片在工作过程中,不可避免地要承受温度、离心和气动等多种动静载荷,叶片易产生高周疲劳破坏。在实际工程应用中,常采用叶冠装置以实现减振目的。带冠叶片干摩擦阻尼减振机理是利用叶冠间初始装配压力和其旋转过程中的回扭力,使叶冠间获得适当的初始法向载荷,并依靠冠间接触面上摩擦耗散振动能量,以减小叶片振动。并且,由于叶冠接触面之间的约束作用,会间接改变叶片的刚度,可以实现对叶片固有频率的调节,避免叶片产生共振。
在国内外现有的研究中,常采用带有迟滞弹簧的宏观滑移摩擦模型的叶片集中参数模型研究叶片在干摩擦阻尼结构下的动力学特性。Griffin利用带弹簧的库仑摩擦模型研究了涡轮叶片的共振响应,并通过实验测试验证了分析结果。考虑随接触面滑动速度变化的摩擦系数的影响,wang和shieh建立了具有干摩擦结构的叶片单自由度模型,并讨论了变化的摩擦系数对叶片振动特性的影响。为提高计算效率,Wang和Chen在前期研究的基础上,采用多谐波平衡法求解带有干摩擦阻尼结构的叶片动力学响应,在保证求解精度的基础上,大大提高了求解效率。Sanliturk等将干摩擦阻尼等效成复刚度模型,并采用谐波平衡法,提出了一种在频域内求解叶片振动响应的方法。李琳等采用时频转换法与高阶谐波平衡法相结合的方法,研究了干摩擦叶片在受到多阶次谐波激励下的叶片减振特性。Sayed等分析了接触状态的变化对带有干摩擦阻尼系统的振动特性及能量耗散的影响,指出了接触状态的变化对冠间摩擦耗能具有很大的影响。Laxalde等采用集中参数模型对叶盘进行建模,并利用多谐波平衡法和时频转换法计算了在周期性激励下系统稳态响应。王小宁等采用宏观滑移摩擦模型,通过接触分析获得冠间摩擦力和相对滑移量,进而求取冠间的等效阻尼和等效刚度,并利用ANSYS软件中MATRIX27弹簧阻尼单元模拟冠间阻尼和刚度,分析了带冠叶片的减振特性。
一些学者分析叶片干摩擦结构减振特性时,考虑了叶片振动对冠间法向载荷的影响。假设法向载荷随着切向位移线性变化,Menq等提出了一种近似方法求解受到变化法向载荷的叶片的动态响应,并采用数值算法验证了所提解法的正确性。Yang等建立了可以考虑切向和法向相对运动的二维接触模型模拟叶冠摩擦接触,并研究了冠间接触表面在分离、黏滞和滑动状态所引起的系统非线性动力学特性。考虑到可变的摩擦系数和法向载荷的影响,Santhosh等研究了在恒定和变法向载荷下两自由度模型的干摩擦动力学特性,并且在可变的法向载荷下发现了如跳跃这样的典型非线性动力学现象。上官博等在Csaba摩擦模型的基础上发展了一种能够考虑接触面摩擦运动过程中正压力随时间变化的微滑移干摩擦模型,克服了Csaba摩擦模型只能描述局部微滑移摩擦力,而不能考虑变化的法向载荷的缺点。
随着研究的继续深入,一些学者采用微滑移摩擦模型模拟干摩擦阻尼结构。将微滑移模型应用于B-G叶片模型,Hudson和Sinha利用谐波平衡法计算了系统的振动响应,并将计算结果同在宏观摩擦模型结果进行对比。为了进一步比较微滑移摩擦模型和宏观滑移摩擦模型,Marquina等分别使用宏观和微滑移摩擦模型,对干摩擦结构进行模拟,并将其结果与通过实验获得的结果进行了对比。Ramaiah和Krishnaiah建立了可以模拟摩擦界面参数的数学模型,并通过实验测试验证了所建立数学模型的有效性。Yuan等利用微滑移摩擦模型研究了阻尼叶片的振动特性,在研究过程中将阻尼叶片简化成两自由度集中质量模型,研究了阻尼器位置对叶片振动响应的影响。利用与文献相同的摩擦模型,Giridhar等分析了阻尼叶片的振动响应,并通过台架试验验证了仿真结果的正确性。为了研究法向运动对微滑移摩擦模型的影响,Cigeroglu等提出了一种可以考虑法向运动引起的压力变化的二維微滑移摩擦模型,并通过一维梁模型和有限元叶片模型两个实例来研究接触界面和摩擦力的特征。漆文凯和张云娟以带缘板阻尼块涡轮叶片为研究对象,建立了二维整体一局部统一的滑动模型,并通过有限元软件分析了不同参数对带缘板阻尼块叶片的振动响应。张亮等基于微滑移摩擦模型建立了叶根阻尼结构干摩擦力本构关系,采用等效椭圆代替阻尼器力与位移函数关系的迟滞回线以获得阻尼结构的等效阻尼和等效刚度,将等效阻尼、等效刚度引入到叶盘系统模型,并采用谐波平衡法求解系统振动响应。为了支持理论分析的结果,一些研究人员同样采用实验方法研究带有干摩擦阻尼叶片的动态特性。
通过对现有文献的调研,可以发现,大部分研究是采用集中参数模型对带有冠间接触的旋转叶片进行建模,然而这种模型并不能考虑叶片安装角和扭角等几何特征对干摩擦叶片动力学特性的影响,并且一些研究已经证明安装角和扭角对带冠叶片动力学特性有很大的影响。因此,建立更准确的带冠叶片动力学模型对研究其干摩擦动力学响应和减振特性具有十分重要的意义。此外,现有文献很少有考虑叶冠倾角对带冠叶片减振动力学特性的影响。为了弥补诸如此类的不足,本文建立了考虑安装角和扭角的干摩擦叶片动力学模型,讨论了叶片安装角和扭角等参数对带冠叶片动力学和减振特性的影响,并通过有限元方法验证了求解结果。
1考虑冠间摩擦的扭形带冠叶片动力学模型建立
由于装配预紧载荷以及叶片旋转导致的回扭力的作用,扭形带冠叶片之间存在很大的法向接触载荷,在法向载荷的作用下,相邻叶冠接触表面将会处于黏滞、滑动以及黏滑共存的接触状态,由于冠间摩擦效应的存在,会对叶片振动起到抑制的作用,考虑冠间摩擦的扭形带冠叶片模型如图1所示。图中,oxyz表示叶片局部坐标系,假定冠间接触面之间具有恒定法向预紧载荷N0,叶冠和叶片截面具有一定的倾角α,vL和wL分别表示叶尖在叶片局部坐标系中的法向和切向位移,vs和ws分别表示叶尖在叶冠接触表面上的法向和切向位移。Ff,μ和kt分别表示接触面上摩擦力、叶冠间的摩擦系数和叶冠切向接触刚度。xs1和zs2分别表示叶冠的切向位移和接触点切向位移(zs1=ws)。
如图1所示,考虑冠间摩擦扭形带冠叶片动力学模型主要包括旋转扭形带冠叶片和冠间摩擦接触两部分建模。针对旋转扭形带冠叶片建模:考虑叶片在旋转过程中产生的离心刚化、旋转软化、科氏力效应以及气流激振力对旋转带冠叶片的影响,基于Timoshenko梁理论,将带冠叶片简化为自由端带有叶尖质量且具有安装角和扭角的悬臂梁,采用Hamilton能量原理建立旋转带冠叶片的动力学模型。旋转带冠叶片能量表达式推导以及主要建模过程可参见文献,旋转带冠叶片运动方程如下:
(6)式中M,G,D,Ke,Kc,Ks,Kacc,q和F分别是质量矩阵、科氏力矩阵、瑞利阻尼矩阵、结构刚度矩阵、离心刚化矩阵、旋转软化矩阵、加速度导致的刚度矩阵以及正则坐标系下的位移向量和外激振力向量,各矩阵具体的表达式和详细的建模过程可参见文献。
针对冠间接触模型,本文采用带有迟滞特性的宏观滑移模型进行建模,迟滞弹簧用来模拟接触面在进行整体滑移之前的弹性变形。假定叶冠接触表面法向载荷保持恒定,即忽略叶片法向振动对法向载荷的影响。在此假设下,叶冠接触面之间会存在三种接触状态,即纯黏滞、黏滑共存和纯滑移,不同的接触状态接触面具有不同的摩擦力,导致系统具有非线性特性,针对这种冠间接触非线性问题,本文拟采用New-mark-β数值方法对动力学方程进行求解。
根据带有迟滞弹簧的宏观滑移摩擦模型中相对位移与摩擦力的关系,叶冠接触面之间的摩擦力Ff的表达式如下
2安装角和扭角对带冠叶片动力学特性的影响
基于所提方法和有限元理论,本节重点讨论了叶片安装角和扭角对旋转带冠叶片干摩擦动力学特性的影响。通过ANSYS软件建立了考虑冠间接触的带冠扭形叶片模型,如图2所示。其中,通过Beaml88单元模拟旋转叶片,叶尖质量采用Mass21单元进行模拟,冠间接触模型采用Combin40进行建模。
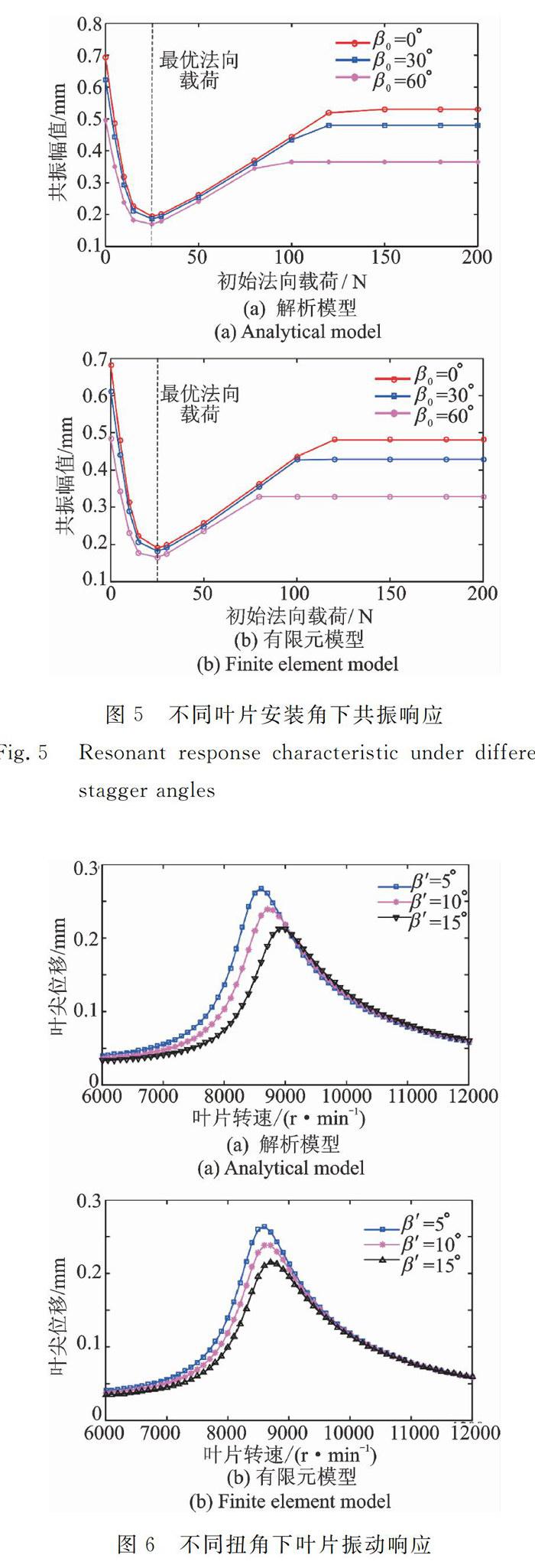
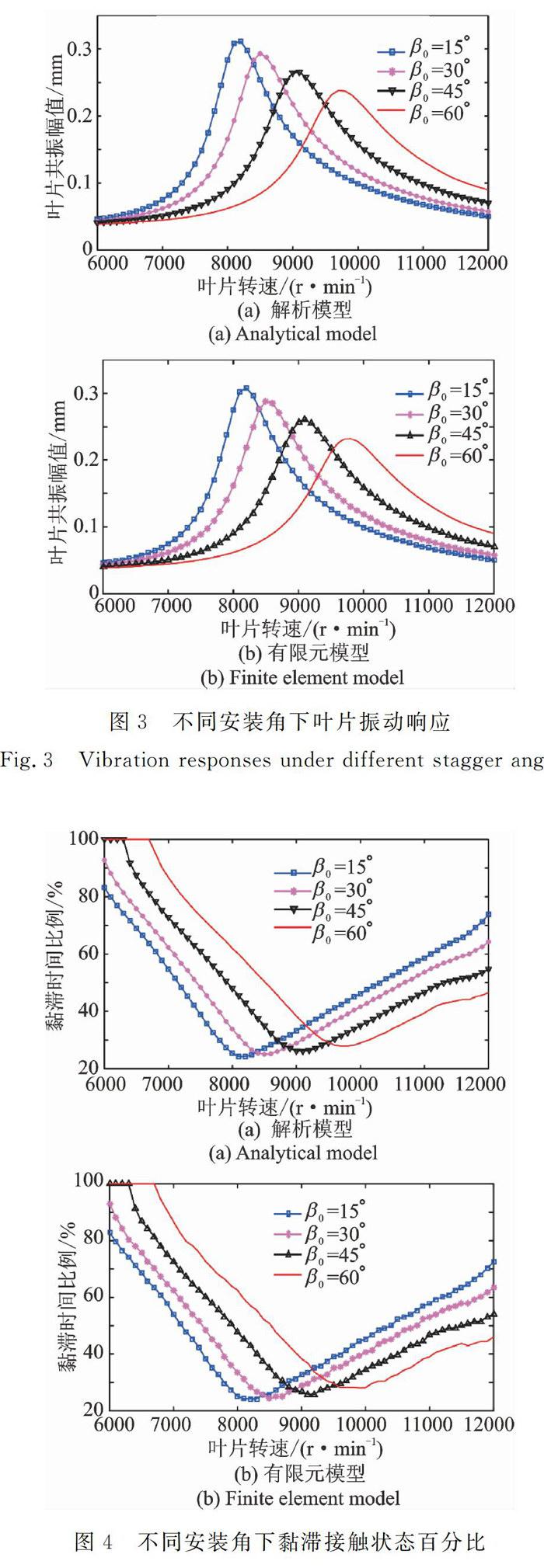
叶片安装角和扭角对叶片固有特性具有很大的影响,它们同样会对冠间接触状态以及减振特性产生很大影响。图3展示了旋转带冠叶片在法向接触载荷N0=10N下,不同安装角下叶尖弯曲位移响应曲线。图4给出了不同安装角下对应的冠间黏滞接触时间百分比。图5给出了不同安装角下,旋转带冠叶片在不同法向接触载荷下叶尖弯曲位移峰值曲线。旋转带冠叶片其余系统参数为kt=1×105N/m,μ=0.3,F0=150N/m(气动力为均布载荷),α=45du3,β=0°。
随着安装角的增加,叶片的共振转速逐渐增大,共振幅值逐渐降低(如图3所示),这说明安装角会增加叶片的刚度。并且,随着叶片安装角的增加,冠间接触表现处于黏滞的时间增加,会对冠间摩擦耗能产生一定的削弱作用(如图4所示)。由图5可以发现,随着安装角的增加,相同法向接触载荷下,共振幅值降低,但带冠叶片最优的法向接触载荷值并没有发生太大变化,这也表明,安装角的变化并不会影响最优法向接触载荷。同时,由图3~5可以看出,本文所提模型和有限元模型具有相同的仿真结果,验证了本文所提方法的有效性。但由于有限元模型节点和自由度较多,求解效率较低。
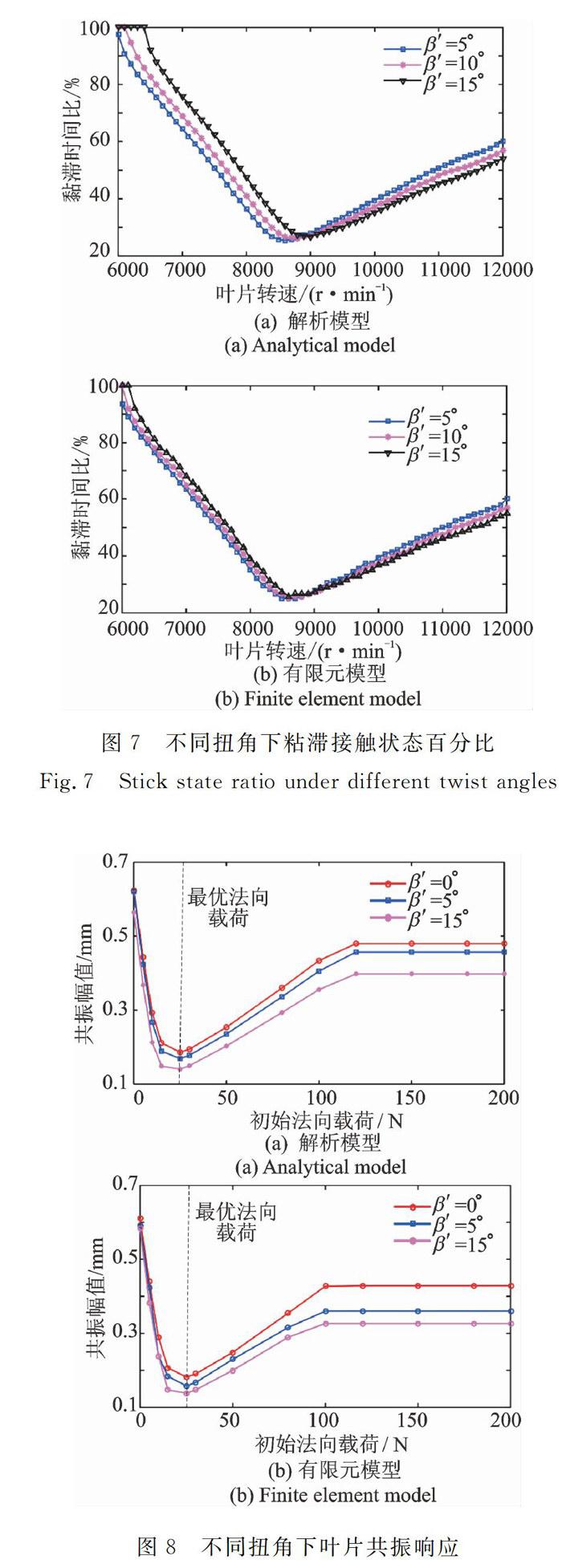
图6展现了带冠叶片在正压力N0=10N,不同扭角下叶尖弯曲位移响应,图7给出了对应参数下冠间接触表面黏滞状态所占时间百分比,图8给出了不同扭角下,旋转带冠叶片叶尖弯曲位移峰值曲线。叶片其余参数为kt=1×105N/m,μ=0.3,F0=150N/m,α=45°,β0=30°。
由圖6~8可以看出,随着扭角的增加,叶片的共振转速逐渐增大,共振幅值逐渐降低,这说明扭角和安装角的影响相似,同样会增加叶片的刚度。并且,随着扭角的增加,叶冠接触表面进入和退出滑动状态的转速增加(如图7所示)。同样,由图8可以看出,叶片扭角的增加,会使共振幅值降低,并且扭角的增加并不会对最优法向载荷产生影响。
3结论
考虑相邻叶冠间的摩擦接触,采用带有迟滞特性的宏观滑移模型模拟冠间摩擦,建立了干摩擦扭形带冠叶片的动力学模型,提出了一种扭形带冠叶片干摩擦动力学响应的求解方法,并分析了叶片安装角、扭角等参数对带冠叶片动力学特性和减振性能的影响,然后通过有限元方法验证了求解结果。结果表明:(1)相邻叶冠接触面上存在一个最优法向接触压力,使叶片减振性能最好;(2)随着安装角和扭角的增加,系统的固有频率增加并且叶片振动响应变弱,并且会削弱冠间接触表面的减振效果,但并不会对最优法向接触压力产生影响。同时,本文所提求解方法相对有限元方法,不仅具有较高的求解精度,而且具有较高的求解效率。