百万等级核电汽轮机组转子热应力计算和控制

张亚平，王强，王尧

（东方电气自动控制工程有限公司，四川德阳，618000）

0　引言

随着电网容量逐年增大，电负荷峰谷差也随之增大，原本带基本负荷的核电汽轮发电机组逐渐开始参加到调峰运行，致使其启停次数增加，负荷变化频繁。变工况下，转子温度场因表面温度的变化而改变，将产生膨胀或收缩变形。这种热变形受到转子本身金属纤维的约束，则会在内部形成应力，即为转子热应力。

转子热应力过大，会导致其低周疲劳损耗，缩短转子使用寿命；因此汽轮机控制系统必须对转子热应力进行实时监视和控制。国内现已投运核电百万机组的控制系统多为进口，其热应力计算或无、或设置黑匣子，无法转化或应用到国产核电机组控制系统中。

论文旨在研究核电汽轮机组转子热应力计算原理，基于通用的差分法计算，定义其在控制系统中的实施细节。

1　汽轮机转子热应力计算理论

转子热应力计算重在计算转子温度场，而转子温度场的计算通常采用解析法或有限元法。有限元方法虽可得到精确的转子热状态，但因其计算量大，不适用于控制系统实时计算。在解析法中，采用一维差分法是较合适的热应力在线计算方式。

表1是用于转子热应力计算的各参数说明。

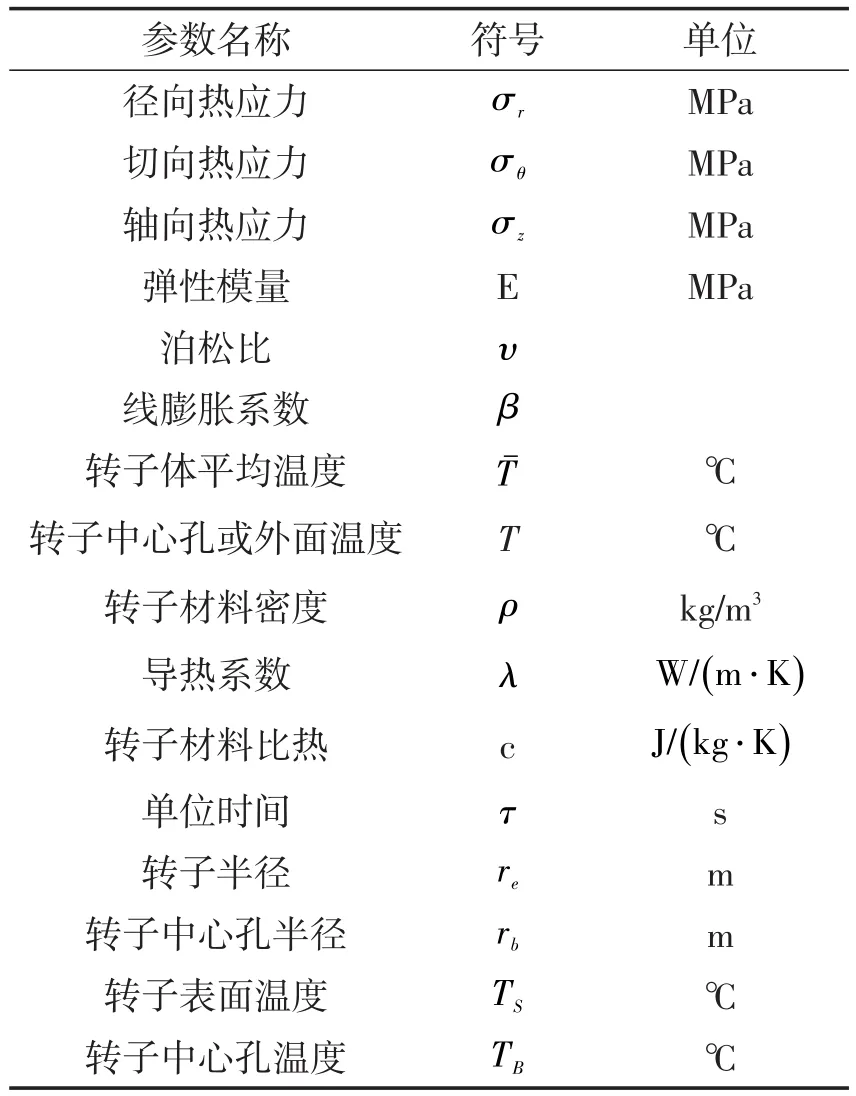
表1　热应力计算参数说明

假设转子为无限长的空心圆柱体，此时温度分布是轴对称的。在转子横截面上，从转子外表面向中心孔表面将转子均分为m等分。

1.1　转子温度场计算公式

设第i段转子在任意时刻（nτ，n为大于1的自然数）的温度分布为：Ti(nτ)。根据牛顿冷却定律，可以推导出以下公式：

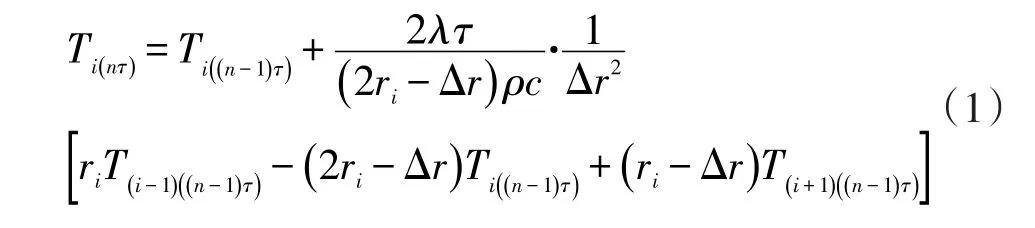
由于转子表面和中心孔边界处，热量传递的介质是不同的。因此式（1）仅用于计算第（2≤i≤m-1）部分转子温度。

第1部分转子在任意时刻的温度分布为：

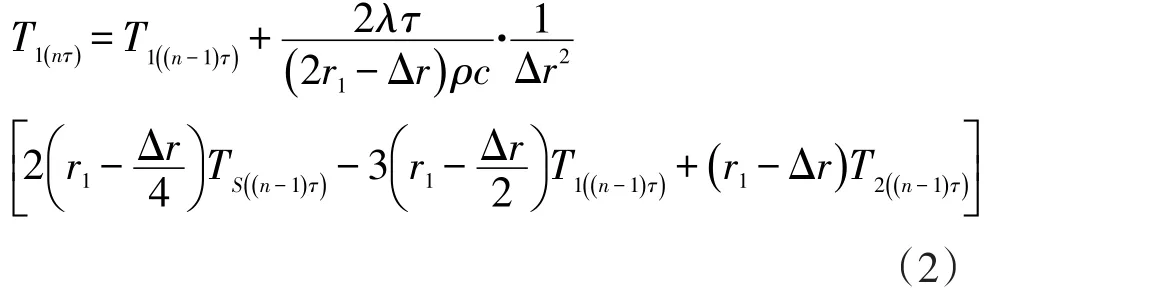
对于第m部分转子在任意时刻的温度分布为：

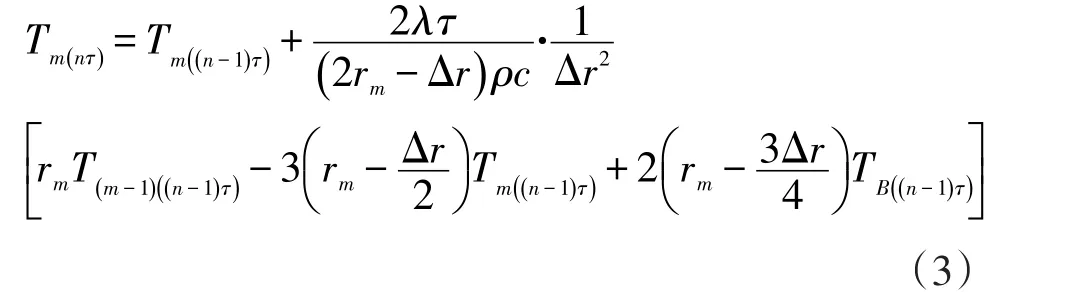
转子中心孔表面在任意时刻的温度分布为：

1.2　转子表面温度

对于转子表面温度的测量方式，传统采用温度测量传感器直接检测转子表面附近蒸汽温度；也有采用非接触红外测温方式，直接测量得出。本文采用测量第一级级前压力，再通过转换公式计算出转子表面蒸汽温度。转换公式为：

式中，a、b、c均为常数，与机组本身的参数相关；X为第一级级前压力，参考点位置为高压第一级叶轮后倒圆角处截面。

1.3　转子平均温度计算公式

通过上述各式，可以计算出转子各部分实时温度分布。设ΔMi为第i段转子的质量（kg），通过式（6）计算转子质量平均温度。

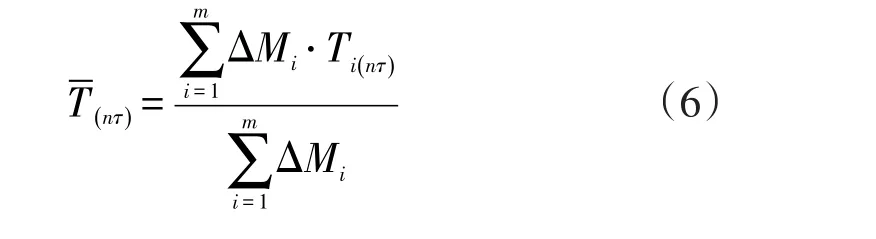
1.4　热应力计算通用表达式

又根据热弹性广义虎克定律，以及转子表面和中心孔处径向热应力为0的边界条件，经过复杂推导，可以得到以下结论：

·转子任意点径向热应力σr较低。

·切向和轴向热应力相等且在转子内外表面达到最大值，其通用表达式为：

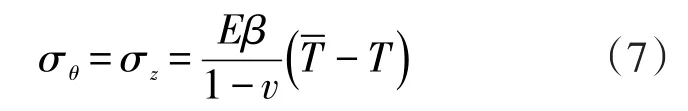
式中，E、β、v在转子材料确定后，可根据材料试验结果获得。

2　逻辑实施细节

2.1　转子均分

根据差分法理论，在转子横截面上，应从转子表面向中心孔表面进行均分。均分份数越多，热应力计算结果越精确；但这也会引起控制器负荷率越高，不利于控制器实时计算和长期运行。

如图1所示，从转子外表面向中心孔表面将转子均分为20等分；根据“1.1节转子温度场计算公式”中的各计算公式，计算每份转子的实时温度。

图1　转子均分图

2.2　转子材质说明

对于确定的机组，转子半径、中心孔半径和密度是确定的。但部分参数会因转子材料热状态的改变而发生变化。对于这些参数，应采用插值法求得实时值。

线膨胀系数、弹性模量、泊松比将采用转子上一单位时间转子平均温度作为输入条件；导热系数和比热将采用转子相应部分上一单位时间的温度作为输入条件。

2.3　关于单位时间τ

单位时间越小，热应力实时计算越接近实际值，但应遵循以下原则：

（1）逻辑实施应根据控制器负荷率进行调整；

（2）为便于逻辑运算，单位时间选用控制器执行周期的倍数；

（3）考虑工艺要求，单位时间最长不超过1s；

2.4　热应力计算的开始

在控制系统中，热应力计算应该是实时进行的，不能被手动切除。当控制系统投入，热应力计算便已开始，因此应该确定转子各部分用于计算的起始温度，即Ti(0)。

2.4.1转子表面温度

当汽轮机挂闸，高压调节阀开启，主蒸汽进入高压缸时，应根据式（5）计算出转子表面温度，即转子表面温度参考高压缸进汽压力。在高压调节阀后，一级叶片之前设置压力测点，采用三冗余的压力变送器进行测量。

考虑在蒸汽未进入汽缸时，热应力计算已经投入，此时转子表面温度可参考高压缸缸体温度。在高压缸进汽法兰金属上设置温度测点，采用冗余的双支热电偶进行测量。

取汽轮机未遮断且机组转速高于盘车转速作为主蒸汽进入高压缸的条件。

转子表面温度的计算逻辑见图2。

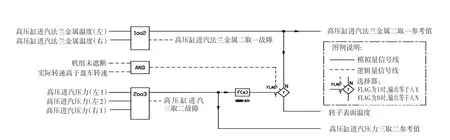
图2　转子表面温度计算逻辑

2.4.2热应力计算失效

热应力计算实时进行，不能被手动切除，但在以下情况时，热应力计算将失效：

（1）高压缸进汽法兰金属温度2取1测量故障；

（2）高压进汽压力3取2测量故障。

以上两种故障均可能由传感器故障，测量链路故障或冗余传感器测量值偏差较大所引起。在故障出现时，将造成热应力计算的参考参数不准确，热应力计算不可用。此时，转子各部分温度结果跟随转子表面温度，热应力计算结果为0，控制系统发出报警。热应力计算从不可用切换至可用的时刻（即热应力计算投入的时刻），转子各部分的初始温度亦采用当前的转子表面温度。

2.5　转子温度场

转子温度场的计算应采用1.1节中的各计算公式，因此应该对各公式进行分解。以第一部分转子为例，式（2）中ρ，τ，r，Δr均为确定的常数，即可以设：

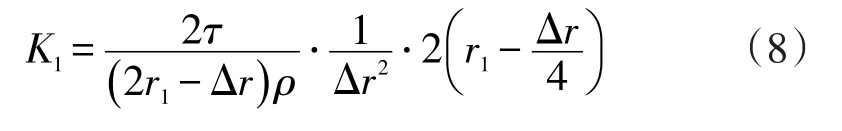
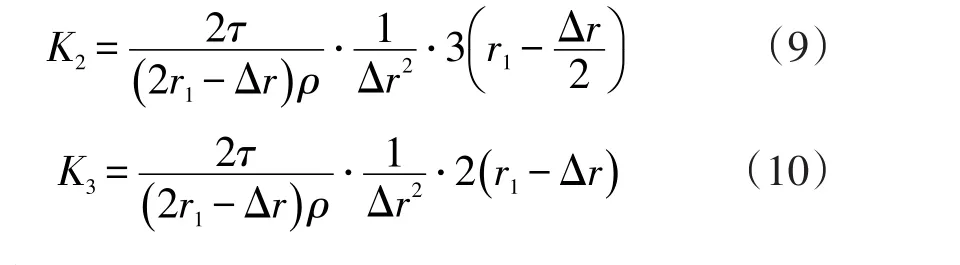
为减轻逻辑复杂程度，通过计算，可以得到K1，K2，K3的实际数值。

带入式（2），即可得到：

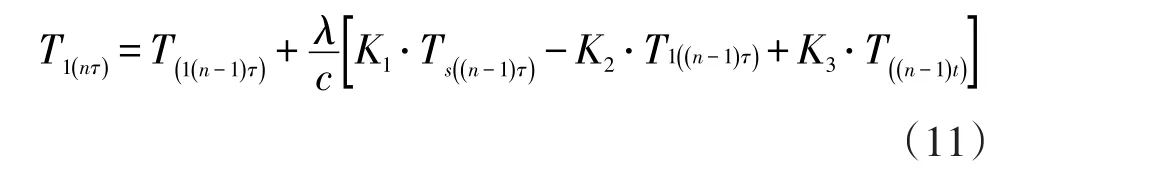
式中，当前温度与上一单位时间的该部分转子温度及相邻部分转子温度密切相关，因此逻辑搭建中将各部分转子温度的逻辑进行分页，对每页逻辑设置其执行周期等于τ。有以下目的：

（1）每一页逻辑每τ的时间执行一次，页内的输入信号（该部分转子上一单位时间温度）引用输出信号（该部分转子实时温度）时，即延迟了τ。

（2）对相邻部分转子温度信号的引用，增加模拟量延迟模块，延迟时间设置为τ，即逻辑页与逻辑页之间的相互引用延迟了τ。

可以得到第一部分转子温度逻辑图,见图3。

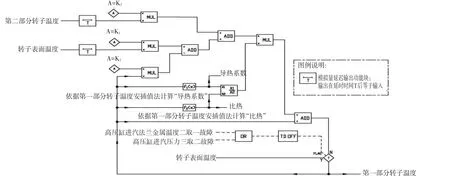
图3　第一部分转子温度计算逻辑

按照上述方法，根据式（5），可以得到转子表面温度的逻辑；根据式（1）可以得到第2至19部分转子温度的逻辑；根据式（3）可以得到第20部分转子温度的逻辑。

此外，中心孔温度按照式（4）进行计算，转子平均温度按照式（6）进行计算，在此不赘述。

2.6　转子热应力

逻辑搭建中按照式（7）进行转子热应力计算，计算转子中心和表面的实时应力，取二者中大值为转子热应力计算值。在逻辑中引入应力集中系数，该系数应能在线调整。

热应力安全裕度的计算公式为：

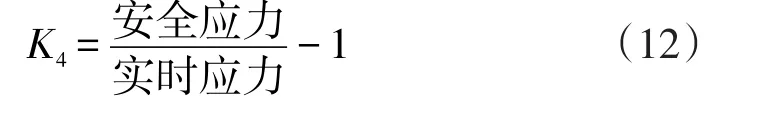
注意在组态时对该公式中的除法运算进行零保护设置。

2.7　关于热应力控制

在汽轮机自动启动（ATC）已经投入的前提下，热应力计算结果影响机组升速率和升负荷率。如针对某机组，工艺将热应力计算结果阀值确定为三档（H1，H2，H3）：

为降低逻辑复杂程度，引入应力参数，应力影响参数直接作用在升速率和升负荷率参考值上，但应该考虑特殊工况，如机组在转速临界区内，特殊工况（如真超速试验），或ATC切除等等。图4是应力参数的相关逻辑结构。

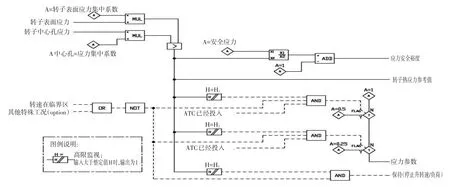
图4　应力参数计算逻辑

以升速率为例，应力参数的逻辑结构如图5所示。

图5　升速率逻辑

升速率须具备手动功能，因此上图的逻辑实施为：机组挂闸后，升速率将被首先选择自动；转速不在临界区或其他特殊工况（如真超速试验进行）时，操作员可以切除升速率自动，采用升速率手动模式，并对手动设置的升速率上限进行限制。ATC投入时，升速率将被锁定在自动，此时，如果转速不在临界区且无其他特殊工况，升速率将受热应力计算结果的影响。升负荷率逻辑结构与此相似。

2.8　人机接口

热应力控制的人机接口草图如图6所示。

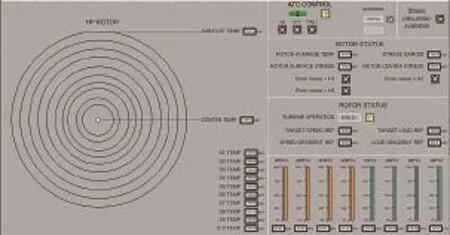
图6　热应力控制人机接口草图

组态实施过程中，在人机接口界面上，应设置专用于热应力的人机接口界面。显示规则为：显示转子各部分实时温度，转子温度按10份（或5份）进行显示，每份的温度是上述20份中从转子表面至中心的依次相邻2份（或4份）的平均温度，计算相邻部分转子的平均温度，应依据式（6）进行；显示转子表面和中心孔温度，以及转子平均温度；显示热应力实际值和热应力安全裕度。

3　结论

根据汽轮机转子热应力计算原理得到核电汽轮机转子热应力计算公式，进而搭建核电汽轮机热应力计算逻辑，和相关控制逻辑。这是采用通用的差分法，实现对热应力计算和控制的逻辑实施细节的研究，继而得到的逻辑架构可以广泛适用于各种硬件平台的控制系统。实现热应力在线计算，为进一步研究核电汽轮机转子寿命损耗的在线计算奠定了基础。

[1]沈士一，庄贺庆，康松，等.汽轮机原理[M].北京：中国电力出版社，1992.

[2]唐军，季佳，刘慧.汽轮机转子的传热分析和热应力计算[J].热力透平,2010,39(3):184-186.

[3]武新华，宋春汀，张新江，等.汽轮机转子热应力简化计算公式的选取[J].汽轮机技术，2000,42(2):20-23.