关于一道解析几何考题的解法探究

郭铭纪

（福建省泉州第一中学，福建泉州　362000）

这题是2013济南市高三3月高考模拟题，笔者把它改编作为一次考试的试题，在考试中，惊喜地发现了学生出现了3种不同的解法，说明了在平常的数学学习中，学生还是能较好地掌握了一些重要的数学思想和方法。笔者也就此题查找了资料，发现基本就2种解法，深入研究，发现了6种不同的解法，各种解法联系了不同的知识体系和数学方法，是一道不错的一题多解的题目。谨以此文谈谈策略性知识的教学对学生的影响。

在数学教学中，一题多解的现象时普遍存在的，每个学生的知识储备是不同的，对知识点的理解程度和角度也是各不相同的。高中数学教材内容有“两多”：知识点多，题型多，因此如果一味地讲究单纯做题而不思考题目背后的东西，是绝对学不好数学的。一题多解正是一个学好数学的好方法，一方面一题多解既让我们复习知识点，又可以发现题目背后知识点之间的联系，从而加深对知识点的理解，而且它还可以锻炼创造性思维和多变思维。

（1）求椭圆的标准方程；

（2）四边形ABCD的顶点在椭圆上，且对角线AC，BD过原点O，

（2）由已知，lAC，lBD的斜率存在且不为 0，设 A（x1，y1），B（x2，y2）

若直线AB的斜率存在，设直线AB的方程为y=kx+m，

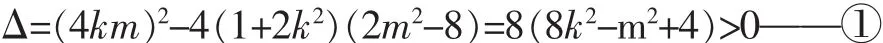
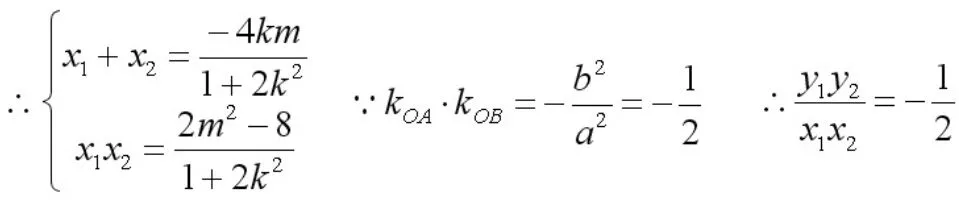
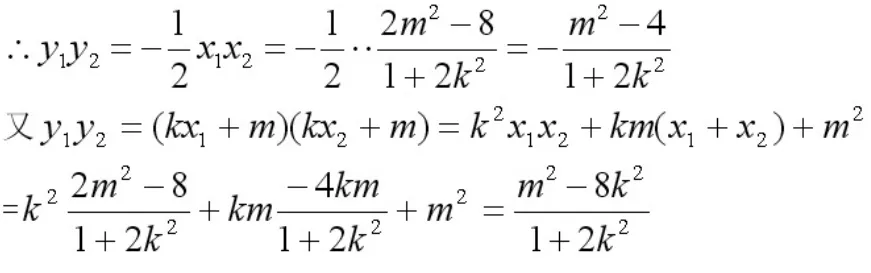
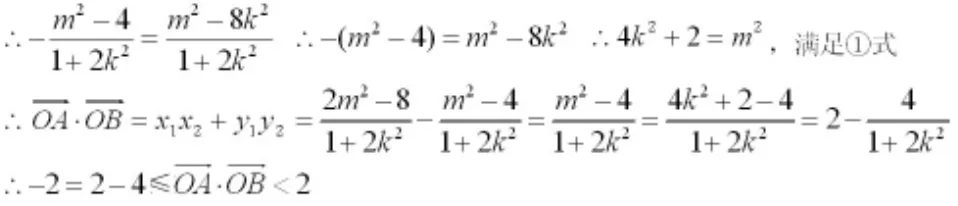
当k=0(此时m2=2满足①式)，即直线AB平行于X轴时的最小值为-2。

评注：通解通法是平常考试中一时想不到其他解法的最直接和可靠的解法，也可以锻炼学生的分析能力，逻辑推理能力，运算能力。

法二(略解)：由已知，lAC，lBD的斜率存在且不为 0，设 lAC：y=kx 设，则由得，同理可得

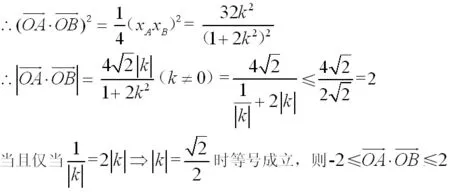
可知： 当 xA＞0，xB＞0 时，当 xA＜0，xB＜0 时

评注：方法二是一种数据的直觉处理方法，利用点的对称性及斜率的关系直接求出点的坐标，把数量积转化为斜率的单变量函数来处理。

以上两种方法为常规常见的解法。通解通法是一种不错的选择。通过对解法（一）（二）的详细讲解，让学生能掌握基本的常规方法，巩固了所学过的知识，突出了本题的重点。仔细分析、挖掘，发现了下面的4种解法，可以作为开拓学生思维，发挥学生的积极主动性的很好的题型。

评注：该解法的思路，也就是利用除双曲线外的几种曲线的动点的最值问题可以用换元法来处理比较简单，椭圆上的动点可以用三角换元来处理。

法四(略解)：设点 A（x1，x1），B（x2，y2），由 x2+2y2=8得

当x1=x2=2时取得最大值2，当x1=-x2=2时取得最大值-2。

评注：这个处理方法和椭圆的第三定义及点差法类似，通过方程来转化为二元变量，利用均值不等式来处理范围问题。另：本种解法也可以转化为y1，y2的不等式问题。

法五 (略解)：同解法四得：x12+x22=8，设

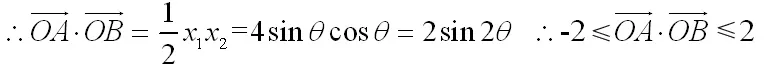
评注：本解法结合解法四和解法三来处理问题。到x12+x22=8这一步骤就可以采用圆的三角换元来处理.

法六(略解)：设点 A（x1，y1），B（x2，y2），则，

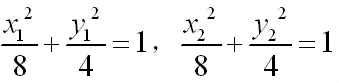
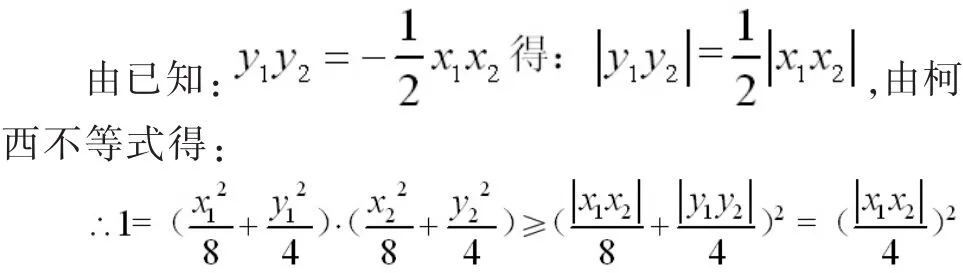
评注：方法四是通过方程以及斜率的关系把变量减少为两个，本解法是通过不减少变量，直接利用四个变量来处理问题。多元变量的处理方法是利用不等式处理最值问题，而柯西不等式可以直接处理x1x2+y1y2问题。

结语：求解题目的方法有很多，通解通法在一定范围内是一种选择。通过对解法（一）（二）的详细讲解，让学生能掌握基本的常规方法，巩固了所学过的知识，突出了本题的重点。另外的几种方法的拓展，利用平常所学的相关性质及解题的方法，不但达到了认知目标，还有利于培养学生的多变思维和创造性思维，让学生寻找更加简练的解题方法，使学生拥有成功的喜悦，提高学习的兴趣。

一题多解和多题一解已广泛应用于数学教学中，尤其是在高三数学复习中，更应强调然一题多解和多题一解，以便解决高强度低效率的复习效果。一题多解中的“题”指一切数学问题，包括基础知识、原理和方法，“解”指对一切数学问题多种不同的理解与解决的过程、策略、方法与结果。可见，一题多解的内涵极其丰富，外延十分广阔。任何解题方法都有其赖以产生的数学基础，而这个基础就是数学教科书的知识、结论、思想方法以及它们之间的内在联系。

[1]赵祥枝.引导学生主动探究，促进数学思维发展的认识与实践[J].中学数学教学参考,2014（5）：35-37.

[2]周来友.一道课本习题的十种证法[J].高中数学教与学,2017（5）：23-25.

[3]周燕伟.女中数学变式教学特点的研究与实践[D].苏州大学,2009.