符合独立五元环规则的C100(417)Cl28形成机理的密度泛函理论研究
尹凡华,谭凯
1 引言
氯化是捕获、分离富勒烯的有效手段,从C50Cl101的合成分离以来,相当多的氯化富勒烯被陆续制备和表征。电弧放电法是制备富勒烯氯化物的主要手段。一种是在电弧放电的条件下引进活性反应气体,如CCl4或Cl2,然后通过高效液相色谱多次分离,从而得到富勒烯氯化物2。另一种是电弧放电之后,初步分离出碳灰,然后与VCl4或SbCl5在300-400 °C下反应获得。目前分离捕获并明确表征的最大富勒烯是C1083。迄今为止,获得的富勒烯氯化物可分为三类:第一类,富勒烯母笼是热力学稳定的符合独立五元环规则(IPR)富勒烯,如 C90(46)Cl324,C96(145)Cl225,C108(1771)Cl123等等。第二类,富勒烯母笼是non-IPR富勒烯,是由其他相对稳定的碳笼氯化中发生 Stone-Wales (SW)转变6而来(SW转变如图1c中所示,由一对五元环和一对六元环围绕的 C―C键发生90°的旋转后,五元环与六元环的相对位置发生了改变),如#18917C76Cl247,8,#39173C82Cl289,#283794C102Cl2010。第三类,富勒烯母笼不是经典富勒烯,它是通过碳笼经获得/失去C2片段而形成,如C88(NC)Cl2211和C98(NC)Cl26(NC表示含一个七元环的非经典富勒烯)。
Yang等人通过低温氯化反应,相继分离并表征了 C100(18)Cl28/30,C100(417)Cl28,C100(425)Cl22和C100(NC)Cl18/22以及C98(NC)Cl2612。C100(18)和C100(425)富勒烯的获得很容易理解,过去的理论计算13,14都显示它们是较稳定的IPR富勒烯,但是C100(417)的获得令人意外。PM3的计算13表明它的能量比最稳定的C100(449)高出78.2 kJ·mol-1,依据波尔兹曼分布推测其丰度是很低的。另外,Yang等人实验细节显示如果仅用C100碳灰氯化得不到C100(417)Cl28产物,实验中是使用C98、C100和 C102碳灰混合物。众所周知,富勒烯的生长过程存在SW转变和C2得失15-17的骨架转变。在低温氯化的条件下,骨架转变也能发生11,18-20,Yang等认为 C98(NC)Cl26就是 C100(417)Cl28失去 C2碎片而形成的。依据富勒烯生长道路,C100(417)Cl28形成的几种可能途径见图1。C100(417)Cl28是由其它稳定IPR C100碳笼加氯而发生SW6转变而得到的?或者是由其它碳数富勒烯骨架转变而来?它真正的生成机理是如何的呢?这些问题还没有人进行过理论上的探讨。因而本文将使用DFT方法对 C100(417)及其氯化物进行计算研究,探索其生成过程不同的反应路径。这些研究将会对为富勒烯的形成机理提供重要线索,为实验工作提供理论解释。
2 模型与计算方法

图1 (a) C100(417)骨架转变示意图; (b) C100(417)Cl28四条可能生成途径;(c)碳笼C100(445)通过C100(419)转变到C100(417)的拓扑关系Fig.1 (a) Skeletal transformation of C100(417); (b) four possible routes to C100(417)Cl28; (c) reconstruction of a skeletal transformation of C100(445) into C100(417) νia C100(419).
对于富勒烯C100,经典异构体数为285913个,其中满足IPR的异构体数为450个21。我们考虑IPR C100(417)富勒烯相对稳定性,对富勒烯C100的450个异构体进行了密度泛函理论 B3LYP/6-31G*22水平的几何结构优化计算,并在相同基组水平下进行了频率计算。对实验上获得能量比IPR C100(417)低且能发生 SW 转变成它的 6个异构体考察温度对异构体相对含量的影响。考察了 C100的异构体之间SW转变,进一步考虑氯化后的SW转变和骨架转变。理论计算所得各过渡态均有唯一虚频,通过内禀反应坐标(IRC)23计算和频率振动分析进一步确认了过渡态的合理性。由于富勒烯氯化后具有太多的可能结构,我们未考虑氯重排的情况,仅用实验获得的氯化富勒烯结构进行研究。所有的计算采用Gaussian 0924软件包下进行。
3 结果与讨论
3.1 C100的450个lPR异构体稳定性
IPR C100在B3LYP/6-31G*水平上进行几何优化的结果列在表1中,包含排序、相对能量(∆Ε)、最高占据分子轨道(HOMO)和最低未占据分子轨道(LUMO)之间的能量间隙(gaps)。我们只列出相对能量在 40 kJ·mol-1以内的计算结果以及C100(419)和C100(417),完全结果可见附表S1(Supporting Information)。计算显示C100(449)是最稳定的异构体。这与过去的PM313,14,AM125以及 PBE1PBE/6-311G*26计算结果是一样的。特别是 B3LYP/6-31G*与 PBE1PBE/6-311G*计算的最稳定的前5个异构体能量排名完全一致。B3LYP/6-31G*计算结果表明C100(417)比最稳定的C100(449)高出71.97 kJ·mol-1。通过 SW转变为C100(417)且稳定性比 C100(417)好的富勒烯是 C100(445)和C100(419),这两种异构体比最稳定的 C100(449)分别高出 33.89 和 55.87 kJ·mol-1。
3.2 温度-相对浓度关系
虽然以上计算的相对能量能够大致描述分子的稳定性,但是不能够提供异构体相对浓度或含量的信息。富勒烯是电弧放电的环境下形成的,必须考虑温度效应。我们进行了谐和振动频率分析,在优化好的结构的振动频率基础上获得转动-振动配分函数,各异构体的相对含量wi可通过下列方程式估算得到。其中qi为配分函数,△H0,i为异构体的基态能量,R为气体常数,T为绝对温度:
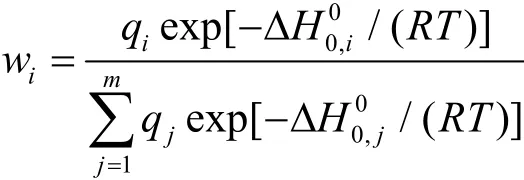
因此我们选取了最稳定异构体 C100(449)和C100(18)、C100(425)、C100(417)、C100(382)、C100(445)和C100(419),基于以上平衡统计热力学原理27绘制了相应的温度-相对浓度曲线(如图2所示)。从图2可以看出,在温度升高时,尽管C100(449)仍处于主导地位,但是相对含量逐渐下降。C100(382)、C100(445)、C100(419)和 C100(417)的含量逐渐升高。C100(445)、C100(419)和 C100(417)在温度达到 1500 K时,其相对含量分别只有 1.17%,0.42%和0.1%。这说明C100(445)和C100(419)在C100碳灰中丰度要高于C100(417),因而存在着C100(445)和C100(419)氯化经过SW转变为C100(417)氯化物的可能。

表1 C100 IPR异构体的相对能量(Er单位kJ·mol-1)与HOMO-LUMO能隙(Egap单位eV)Table 1 Relative energies (Er in kJ·mol-1) of the C100 IPR fullerene isomers and HOMO-LUMO gap (Egap in eV).

图2 C100的七个异构体相对含量与温度的依赖关系Fig.2 Dependence of relative concentration of the seven isomers of C100 on temperature.
3.3 通过Stone-Wales转变生成C100(417)
为了考查 C100(445)和 C100(419)富勒烯氯化物通过SW转变生成C100(417),构造了C100(445)Cl28和 C100(419)Cl28,前者进行一次 SW 转变变为后者,再进行一次 SW 转变为最终实验上获得的产物,见图 3。计算结果显示从 C100(445)Cl28到C100(419)Cl28的 SW转变活化能是 258.58 kJ·mol-1;从C100(419)Cl28发生第二次SW转变成C100(417)Cl28时,活化能是 262.44 kJ·mol-1。对于相反的过程,SW转变活化能要大。即SW转变过程是放热的,是能量有利的过程。相比较空笼的SW 转变,C100(445)到 C100(419)转化的活化能是625.22 kJ·mol-1;当发生第二次SW转变时,活化能是579.87 kJ·mol-1。这与过去计算富勒烯空笼发生 SW 转变所需的能量接近28。显然,加氯之后发生的 SW 转变所需的能垒大大降低,从而使得在低温氯化的条件下发生 SW 转变是相对容易得多,这与之前加氯有助于发生 SW 转变的报道是一致的7,9,10。因此,在不高的温度下,C100(445)和C100(419)氯化后通过之间的 SW 转变可以转变为C100(417)Cl28产物。
3.4 不同碳数富勒烯间骨架转变为C100(417)
考虑相同碳数 C100富勒烯通过 SW 转变获得C100(417)后,我们进一步探讨不同碳数富勒烯经过骨架转变成为C100(417)的过程。选取实验上已经捕获的C98(NC)12为起始物与C2发生加成反应,即可生成 C100(417)。图 4所示无氯和有氯条件下从C98(NC)到C100(417)的过程的加成反应路径。无氯条件下 C98(NC)经过 C2插入的反应能垒为 112.89 kJ·mol-1,而相反过程反应能垒非常高(690.80 kJ·mol-1)。计算的反应吉布斯自由能为-577.97 kJ·mol-1;有氯条件下 C98(NC)Cl26与 C2Cl2反应生成 C100(417)Cl28需要克服的能垒更小(60.61 kJ·mol-1),计算的反应吉布斯自由能为-583.48 kJ·mol-1;两者都是放热过程。因而常温下七元环的C98氯化物非常容易插入C2碎片转变为C100(417)。

图3 C100(445)Cl28通过C100(419)Cl28转变到C100(417)Cl28的关系图Fig.3 Reconstruction of a skeletal transformation of C100(445)Cl28 into C100(417)Cl28 νia C100(419)Cl28.

图4 C98(NC)与C2反应生成C100(417)Fig.4 Reaction pathway of C98(NC) and C2 to C100(417).
另一条骨架转变路径是C102失去C2碎片成为C100(417)。之前的实验报道了 C102最稳定的碳笼C102(603)以C102(603)Cl18/20的形式捕获。如图5所示,C102(603)进行1次SW旋转即可得到C102(580),经过第二次 SW 旋转得到 C102(582)。再经历 SW旋转可以获得非经典七元环富勒烯 C102(NC),这个 C102(NC)可以通过一次 SW 旋转获得另一个C102(NC)。最后通过失去C2碎片获得C100(417)。通过计算它们空笼之间SW旋转能垒,获得的SW旋转活化能垒在610.49到642.61 kJ·mol-1之间。在氯化情况下从 C102(603)Cl18到 C102(580)Cl18的SW旋转活化能是273.47 kJ·mol-1。其它步骤SW旋转也大致相同。从空笼C102(603)到C102(NC),计算的反应吉布斯自由能为 473.01 kJ·mol-1,而C102(603)Cl18到C102(NC)Cl18,反应吉布斯自由能为197.13 kJ·mol-1。
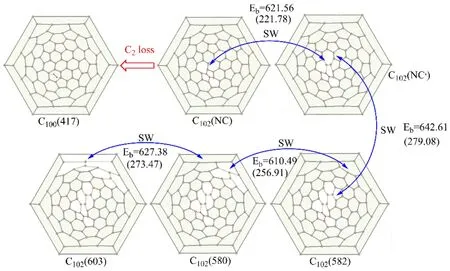
图5 C102(603)发生SW转变到C102(NC)的反应Fig.5 The SW transformation between C102(NC) to C102(603).

图6 C102(NC)失去C2生成C100(417)反应自由能-反应坐标示意图Fig.6 The free energy-reaction coordination scheme of C102(NC) and C2 to C100(417).
进一步我们考查C102(NC)Cl30失去C2碎片生成C100(417)Cl28的反应。图6所示无氯和有氯条件下从 C102(NC)到 C100(417)的反应路径。无氯条件下 C102(NC)经过失去 C2的反应能垒为 622.33 kJ·mol-1,而其逆反应活化能垒相对小(283.67 kJ·mol-1),计算的反应吉布斯自由能为 338.66 kJ·mol-1,反应不能自发进行;而有氯条件下C102(NC)Cl30失去C2Cl2生成C100(417)Cl28只需克服 366.24 kJ·mol-1的能垒,计算的反应吉布斯自由能为94.84 kJ·mol-1。考虑在实验温度628 K时,其计算的反应吉布斯自由能为-45.01 kJ·mol-1,反应能够自发进行。
4 结论
通过对 C100(417)Cl28的形成多种来源途径的密度泛函理论研究,计算结果表明C100(417)Cl28形成的最主要来源是通过 C102(603)骨架转变,即经历氯化、C2失去和SW转变而来。这些结果很好地解释了实验现象,揭示了富勒烯衍生物新的形成机理。
Supporting lnformation:available free of charge νia the internet at http://www.whxb.pku.edu.cn.
(1) Xie, S. Y.; Gao, F.; Lu, X.; Huang, R. B.; Wang, C. R.; Zhang,X.; Liu, M. L.; Deng, S. L.; Zheng, L. S. Science 2004, 304,699. doi: 10.1126/science.1095567
(2) Tan, Y. Z.; Xie, S. Y.; Huang, R. B.; Zheng, L. S. Νat. Chem.2009, 1, 450. doi: 10.1038/nchem.329
(3) Wang, S.; Yang, S.; Kemnitz, E.; Troyanov, S. I. Inorg. Chem.2016, 55, 5741. doi: 10.1021/acs.inorgchem.6b00809
(4) Troyanov, S. I.; Yang, S.; Chen, C.; Kemnitz, E. Chem. Εur. J.2011, 17, 10662. doi: 10.1002/chem.201100908
(5) Yang, S.; Wei, T.; Kemnitz, E.; Troyanov, S. I. Angew. Chem.Int. Εd. 2012, 124, 8364. doi: 10.1002/anie.201201775
(6) Stone, A.; Wales, D. Chem. Phys. Lett. 1986, 128, 501.doi: 10.1016/0009-2614(86)80661-3
(7) Ioffe, I. N.; Mazaleva, O. N.; Chen, C.; Yang, S.; Kemnitz, E.;Troyanov, S. I. Dalton. Trans.2011, 40, 11005.doi: 10.1039/C1DT10256G
(8) Ioffe, I. N.; Goryunkov, A. A.; Tamm, N. B.; Sidorov, L. N.;Kemnitz, E.; Troyanov, S. I. Angew. Chem. Int. Εd. 2009, 48,5904. doi: 10.1002/anie.200902253
(9) Ioffe, I. N.; Mazaleva, O. N.; Sidorov, L. N.; Yang, S.; Wei,T.; Kemnitz, E.; Troyanov, S. I. Inorg. Chem. 2012, 51,11226. doi: 10.1021/ic301650j
(10) Yang, S.; Wei, T.; Wang, S.; Ignat'eva, D. V.; Kemnitz, E.;Troyanov, S. I. Chem. Commun. 2013, 49, 7944.doi: 10.1039/C3CC44386H
(11) Ioffe, I. N.; Mazaleva, O. N.; Sidorov, L. N.; Yang, S.; Wei,T.; Kemnitz, E.; Troyanov, S. I. Inorg. Chem. 2013, 52,13821. doi: 10.1021/ic402556g
(12) Wang, S.; Yang, S.; Kemnitz, E.; Troyanov, S. I. Angew.Chem. Int. Εd. 2016, 55, 3235. doi: 10.1002/ange.201511928
(13) Zhao, X.; Goto, H.; Slanina, Z. Chem. Phys. 2004, 306, 93.doi: 10.1016/j.chemphys.2004.07.019
(14) Cai, W.; Xu, L.; Shao, N.; Shao, X.; Guo, Q. J. Chem. Phys.2005, 122, 184318. doi: 10.1063/1.1891706
(15) Hao, Y.; Tang, Q.; Li, X.; Zhang, M.; Wan, Y.; Feng, L.;Chen, N.; Slanina, Z. K.; Adamowicz, L.; Uhlík, F. Inorg.Chem. 2016, 55, 11354. doi: 10.1021/acs.inorgchem.6b01894
(16) Chen, C. H.; Abella, L.; Cerón, M. R.; Guerrero-Ayala, M. A.;Rodríguez-Fortea, A.; Olmstead, M. M.; Powers, X. B.;Balch, A. L.; Poblet, J. M.; Echegoyen, L. J. Am. Chem. Soc.2016, 138, 13030. doi: 10.1021/jacs.6b07912
(17) Cai, W.; Li, F. F.; Bao, L.; Xie, Y.; Lu, X. J. Am. Chem. Soc.2016, 138, 6670. doi: 10.1021/jacs.6b03934
(18) Yang, S.; Wang, S.; Kemnitz, E.; Troyanov, S. I. Angew.Chem. Int. Εd. 2014, 53, 2460. doi: 10.1002/anie.201310099
(19) Yang, S.; Wei, T.; Scheurell, K.; Kemnitz, E.; Troyanov, S. I.Chem. Εur. J. 2015, 21, 15138.doi: 10.1002/chem.201501549
(20) Jin, F.; Yang, S.; Kemnitz, E.; Trojanov, S. I. J. Am. Chem.Soc. 2017, 139, 4651. doi: 10.1021/jacs.7b01490
(21) Fowler, P. DΕ Manolopoulos An atlas of Fullerenes; Oxford University Press: Oxford, UK, 1995.
(22) Becke, A. D. J. Chem. Phys. 1993, 98, 5648.doi: 10.1063/1.464913
(23) Gonzalez, C.; Schlegel H. B. J. Chem. Phys. 1989, 90, 2154.doi: 10.1063/1.49785
(24) Frisch, M.; Trucks, G.; Schlegel, H.; et al. Gaussian 09,Revision A. 1.; Gaussian, Inc: Wallingford, CT, 2009.
(25) Yoshida, M.; Gotō, H.; Hirose, Y.; Zhao, X.; Ōsawa, E. J.Theo. Chem. 1996, 1, 163. doi: 10.1002/ejtc.26
(26) Shao, N.; Gao, Y.; Yoo, S.; An, W.; Zeng, X. C. J. Phys.Chem. C 2006, 110, 7672. doi: 10.1021/jp0624092
(27) Slanina, Z.; Lee, S. L.; Uhlík, F.; Adamowicz, L.; Nagase, S.Theor. Chem. Acc. 2007, 117, 315.doi: 10.1007/s00214-006-0150-0
(28) Bettinger, H. F.; Yakobson, B. I.; Scuseria, G. E. J. Am.Chem. Soc. 2003, 125, 5572. doi: 10.1021/ja0288744
- 物理化学学报的其它文章
- 类单晶硅结构Si(C≡C―C6H4―C≡C)4新材料的力学与光学性质:第一性原理研究
- Keggin型多酸负载的单原子催化剂(M1/POM, M = Ni, Pd, Pt, Cu,Ag, Au, POM = [PW12O40]3-)活化氮气分子的密度泛函理论计算研究
- Strength of lntramolecular Hydrogen Bonds
- 嵌入配位不饱和金属位对多孔芳香骨架材料储氢性能的影响
- Fukui Functions for the Temporary Anion Resonance States of Be-, Mg-,and Ca-
- 从能量和信息理论视角理解单取代烷烃的异构化

