螺旋式激发的荧光分子断层成像

侯榆青， 魏红娜， 易黄建， 张　旭， 贺小伟

(西北大学 信息科学与技术学院，陕西 西安 710127)

荧光分子断层成像能在体实现生物组织内部荧光标记物(荧光探针或者荧光蛋白)的三维定位和定量分析，目前广泛应用于小动物研究[1]．荧光分子断层成像主要应用于肿瘤的早期检测和药物分布监测等生物医学研究方面，具有成本低、灵敏度高、可用的分子探针种类多等特点，有较广的应用前景[2]．常用的荧光分子断层成像系统可用近红外光照射荧光探针，并使用电荷耦合器件(Charge-Coupled Device，CCD)相机来获得生物组织表面的荧光强度的分布，利用光传输模型和反演算法重建生物组织中荧光探针的分布[3]．

荧光分子断层成像系统经过十几年的研究和发展，大致经历了3大阶段：第1阶段是光纤接触式成像系统，其需要将小动物放入成像腔中，加入匹配液，并用光纤发射和接收信号．但是此系统约束了小动物的体积，以及因光纤的限制只能获得较少的测量数据[4]．第2阶段是半接触式成像系统，在接触式成像系统的基础上使用了电荷耦合器件相机直接接收荧光信号．相比第1阶段，实现简单，但是由于投影角度的减少，导致重建精度比较低[5]．第3阶段是目前常采用的系统，为完全非接触、全角度的成像系统，可以实现360°全视觉扫描，获得更多的测量数据，提高重建的准确性[6]．通常为了使得荧光探针受激发完全，当前全角度的成像系统多采用多点激发、多角度测量的方式获得测量数据，由此带来的数据采集时间随着激发次数和采集数据角度的增加而增加，不利于实现实时测量．

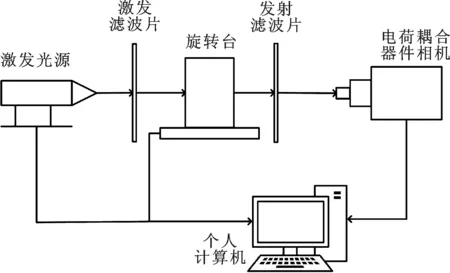
图1　荧光分子断层成像系统示意图

笔者提出一种螺旋式激发的成像方式，使得荧光目标受激发完全．相比于圆周式激发，螺旋式激发的激发点通过一个螺旋式结构分布在成像目标的一周，形状类似螺旋楼梯．此激发方式可在未知荧光目标具体位置的情况下，通过有限次数的激发使荧光目标受激发完全而获得测量数据，进一步提高了重建结果的质量．

1　螺旋式激发的荧光分子断层成像

1.1　荧光分子断层成像系统

实验采用的是非接触、360°几何投影自由空间荧光分子断层成像系统，工作模式为连续波模式，并用计算机控制一系列信号的传递．系统示意图如图1所示，将样本放置到旋转台上，设置好激发点，发射器发射的激发光经过滤波片照射到样本上，经360°旋转产生样本表面光强信息，使得电荷耦合器件相机通过发射滤波片收集激发光源的信号[7]．电荷耦合器件相机可以采集更多的数据信息，使得荧光分子断层成像的重建质量增加，并降低了重建问题的不适定性[8]．

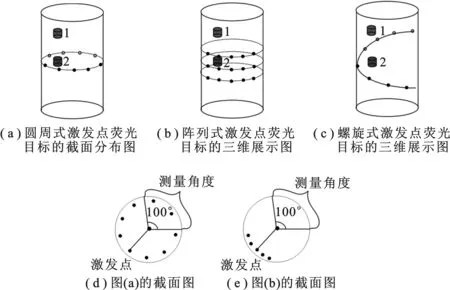
图2　激发方式示意图

1.2　螺旋式激发的成像系统

现有的激发方式多为完全非接触、全角度的点光源激发成像系统，其激发方式多为多点激发、多角度测量，如图2(a)所示；或多点激发、单角度测量，如图2(b)所示．分别将其命名为圆周式激发和阵列式激发．圆周式激发一般激发点等间隔位于同一高度，截面图如图2(d)中所示；而阵列式激发的激发点多为阵列式排列，截面图如图2(e)所示．如果对重建的荧光目标预先未知其大概的位置，若用圆周式激发方式，则会使得激发点照射荧光目标不完全，有可能获得的荧光数据不准确，进一步影响重建误差，如图2(a)中的圆柱1代表荧光目标，激发点所在高度与其相差较大．若用阵列式激发，则需要激发的点数较多，采集数据时间过长．为了解决上述问题，笔者提出一种基于螺旋式激发的方式，如图2(c)所示．无论荧光目标是圆柱1还是圆柱2，螺旋式激发方式中总会有激发点与其位于相当高度．而在系统搭建上，螺旋式激发方式的实现也较为方便．将小动物放置到可进行360°旋转的旋转台上，用激发光照射小动物体内的荧光分子探针．随着旋转台旋转到一定的角度，激光器从上到下改变一定的高度，在规定的高度内正好完成待成像物360°的旋转，形成螺旋式激发．

1.3　逆问题重建模型

基于多点激发方式的荧光分子断层成像，具有高散射、低吸收的特点．光的传输过程可以由激发过程和发射过程组成，分别为[9]

(1)

其中，下标x和m分别表示激发光和发射光;Dx，Dm表示扩散系数;Φx，Φm表示光子通量密度;μax，μam表示吸收系数;ημaf表示荧光产额;Θ表示激发光源强度;Ω表示成像物体所占据的三维空间．

基于有限元方法，对未知荧光目标和光强分布的测量值建立线性关系[10]:

Φ=AX,

(2)

图3　激发点设置示意图

其中，Φ是物体表面荧光光强分布，A是系统矩阵，X表示未知的荧光产额．所有的重建都采用不完全变量截断共轭梯度法[11]．

2　实验验证与结果分析

2.1　激发点的设置

为了验证笔者所提方法的有效性，将螺旋式激发

方式、圆周式激发方式和阵列式激发方式分别进行比较．实验中采用的圆周式激发方式激发点个数为10个，如图3(a)所示；高度相同，每个激发点间隔36°，均匀地分布在成像目标一周，俯视图如图3(d)所示．阵列式激发方式的激发点采用 4×3 的方式，如图3(b)；每行4个激发点，每个激发点间隔为30°，位于x轴正方向，行间距为 3 mm，俯视图如图3(e)所示．螺旋式激发方式激发点同样采用10个激发点，俯视图与圆周式激发点相同，如图3(f)所示；但其高度每个相差 1 mm，激发点最低高度为 -5 mm，依次向上增加，如图3(c)所示．

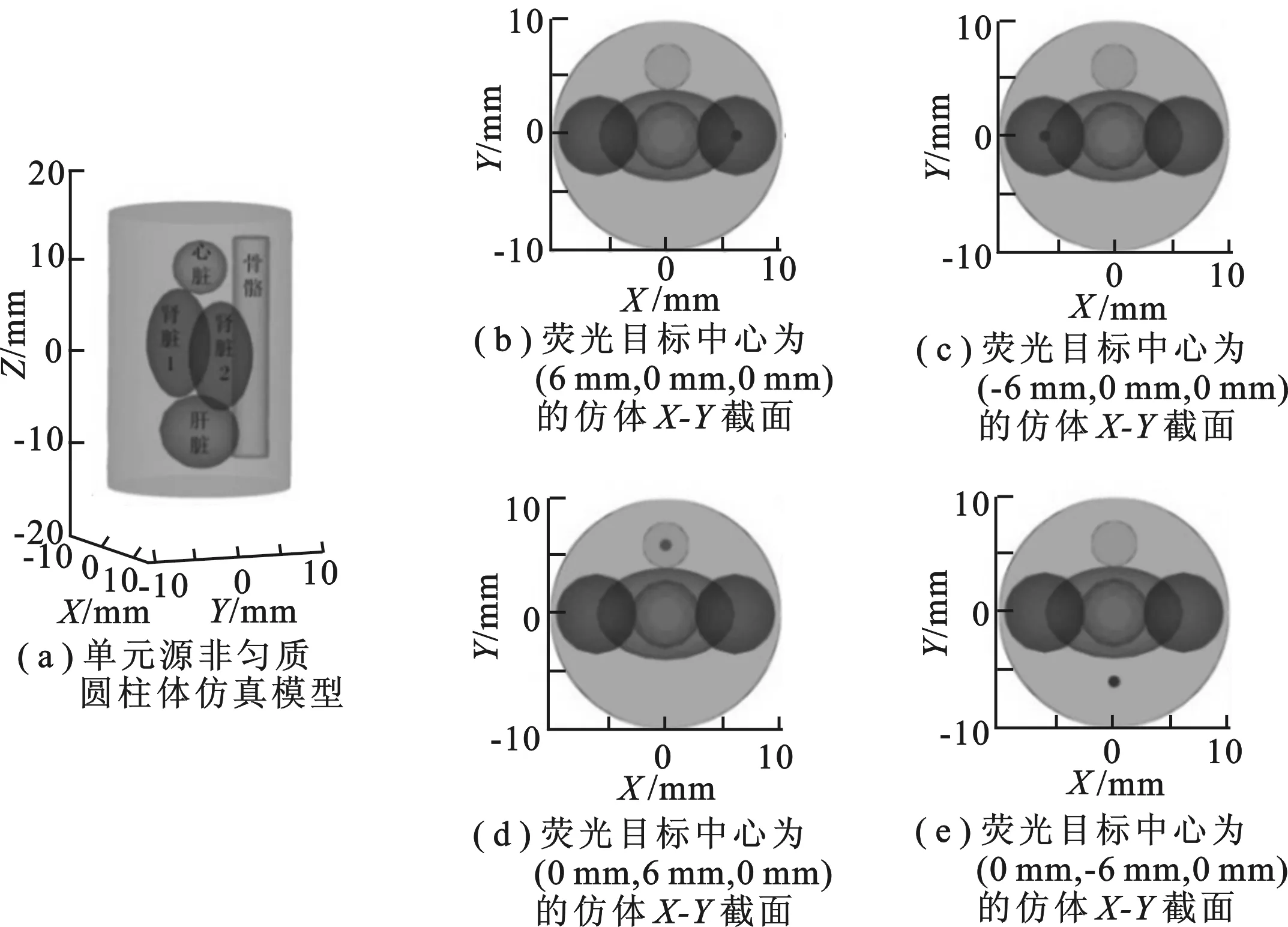
图4　仿真示意图

2.2　单 光 源

为了验证螺旋式激发方式的可行性，用非匀质圆柱形仿体进行仿真实验验证．圆柱模型如图4(a)所示，圆柱半径为 10 mm，高为 30 mm，中心位置设为 (0 mm，0 mm，0 mm)，内部设有5个几何体，分别代表心脏、肝脏、骨骼以及两个肾脏，各个器官的光学参数如表1所示[12]．荧光目标为半径 0.5 mm、高 1.4 mm 的圆柱形仿体．将荧光目标放置在4个不同的位置，中心坐标分别为 (6 mm，0 mm，0 mm)，(-6 mm，0 mm，0 mm)，(0 mm，6 mm，0 mm)，(0 mm，-6 mm，0 mm)，其截面图如图4(b)～(e)所示．对比圆周式激发、阵列式激发和螺旋式激发3种激发方式下的重建结果．其中圆周式激发的激发点分别位于Z= -5 mm，Z= 1 mm，Z= 5 mm 处．

表1　非匀质仿体的光学参数

为了评价重建结果，设计了标准均方根误差(norm Root Mean Square Error，nRMSE)和位置误差(LE)来精确对比上述实验结果．标准均方根误差定义为[13]

(3)

其中，fnRMSE是标准均方根误差;Xr和Xo分别表示重建的荧光产额值和真实荧光产额值．标准均方根误差的值越接近于零，表明重建的结果越精确．

位置误差表示的是重建的荧光目标中心位置和真实的荧光目标中心位置之间的误差，其表达式为[14]

(4)

其中，fLE是位置误差;L=[X，Y，Z]，表示点的坐标向量;Lr和Lo分别表示重建目标的中心位置和真实荧光目标的中心位置．

当荧光目标中心坐标为 (6 mm，0 mm，0 mm) 时，其重建结果如图5第1行所示，其中(a1)、(a2)、(a3)为圆周式激发点分别位于Z= -5 mm，Z= 1 mm，Z= 5 mm 时的结果；图5(a4)是阵列式激发的重建结果；图5(a5)是螺旋式激发的重建结果．图中，黑色的小圆圈表示荧光目标的真实位置．改变荧光目标的位置为 (-6 mm，0 mm，0 mm)，(0 mm，6 mm，0 mm)，(0 mm，-6 mm，0 mm)，其重建结果分别为图5的第2行到第4行．

图5　单光源重建结果X-Y截图面

激发方式中心坐标(6mm,0mm,0mm)nRMESLE/mm(-6mm,0mm,0mm)nRMESLE/mm(0mm,6mm,0mm)nRMESLE/mm(0mm,-6mm,0mm)nRMESLE/mm圆周式Z=-5mm0.661.020.710.741.360.780.450.68圆周式Z=1mm0.130.480.540.490.700.580.400.21圆周式Z=5mm0.520.871.080.930.900.770.540.85阵列式激发0.220.463.901.612.463.340.370.45螺旋式激发0.130.330.530.650.670.640.300.49

表2是4组重建结果的定量分析．从实验结果展示图5和表2可以看到，当激发点远离荧光目标(即圆周式Z= -5 mm 及Z= 5 mm) 时，重建结果较差，位置误差在 1 mm 左右; 阵列式激发只能获取到荧光目标一侧的信息，且距离激发点较近时，获得的数据较好，而远离荧光目标时，则获得的数据不够全面，位置误差大于 1.5 mm，均方根误差大于 2 mm，重建结果十分不理想;而用螺旋式激发方式激发荧光目标可以得到较好的结果，位置误差和均方根误差均在 0.5 mm 左右．由此说明螺旋式激发方式不仅提高了重建精度，而且鲁棒性较好．同时表2也显示出当激发点接近荧光目标时，重建结果比较理想．但是，在现实状况下，荧光目标的位置是未知的，利用螺旋式激发方式比远离荧光目标的圆周式激发方式要有优势，可以获得比其更精确的重建结果．

图6 双光源非匀质圆柱体仿真模型

2.3　双 光 源

为了进一步评估螺旋式激发成像系统的性能，在相同数目的投影数据下，开展双目标重建实验．仿体模型如图6所示．两个荧光目标是半径为 0.5 mm、高度为 1.4 mm 的圆柱形，目标1中心为 (6 mm，0 mm，3 mm)，目标2中心为 (6 mm，0 mm，-3 mm)．圆周式激发中激发光源分别位于Z= -3 mm，Z= 0 mm，Z= 3 mm 处．图7是重建结果，其中圆周式激发点高度分别位于Z= -3 mm，Z= 0 mm 和Z= 3 mm 处．重建结果如图7(a)～(c)所示，分别展示了圆周式激发方式的X-Z横截面的荧光产额值；图7(d)是阵列式激发的重建结果，展示了阵列式激发方式的横截面积的荧光产额值；图7(e)是螺旋式激发的重建结果，展示了螺旋式激发方式的横截面积的荧光产额值．图中，黑色的长方形表示荧光目标的真实位置．

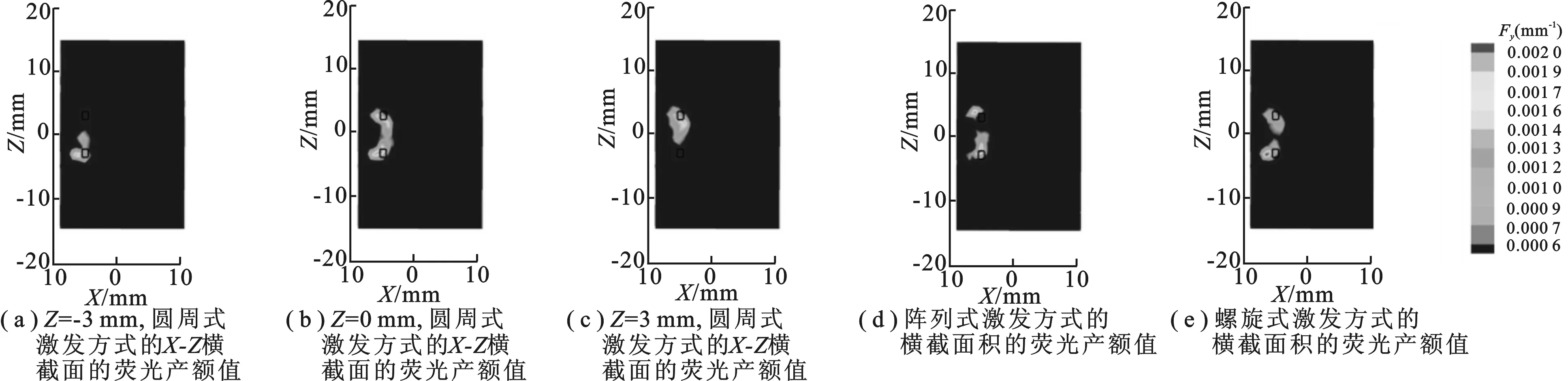
图7　双光源重建结果

表3为双光源重建结果的定量分析．从图7可以看出，圆周式激发点高度分别为Z= -3 mm，Z= 0 mm，Z= 3 mm 时，针对较远的荧光目标采集的信息相对较少，位置误差大于 4 mm，重建结果并不理想; 对于阵列式激发方式，对每个荧光目标只能进行单面激发，重建结果仍无法取得满意的结果，位置误差大于 1 mm; 而螺旋式激发方式，可以收集到两个荧光目标的信息，重建的两个荧光目标的位置误差都小于 1 mm，重建结果相对较好．由此可得，圆周式激发方式针对不同高度的多目标重建结果较差；螺旋式激发方式可以扩大激发范围，获得较多的荧光目标信息，对不同高度的荧光目标重建可以更加准确，得到令人满意的结果．

表3　双光源重建结果

3　总　　结

荧光分子断层成像通过近红外光激发荧光探针，根据生物表面的荧光信号并结合数学模型，可通过重建算法获得荧光探针的三维空间分布．在实际应用中，多数情况下对荧光探针的位置是未知的，这就使得外部光激发荧光探针时，若采用同一高度的圆周式激发方式，可能出现荧光探针激发不完全的情况，由此获得的表面数据会不准确而影响后续的重建．为了克服这个缺点，笔者提出了一种螺旋式激发的荧光数据采集系统．通过仿真实验可以看出，在相同投影数据个数的情况下，相对于远离荧光目标的圆周式激发方式，螺旋式激发方式重建结果的标准均方根误差和位置误差值均相对较小，因此其重建结果较好．

参考文献：

[1] CHEN D, LIANG J, LI Y, et al. A Sparsity-constrained Preconditioned Kaczmarz Reconstruction Method for Fluorescence Molecular Tomography[J]. Biomed Research International, 2016, 2016: 4504161.

[2]ZHAO Y, ZHU D, BAIKEJIANG R, et al. 3D Mouse Shape Reconstruction Based on Phase-shifting Algorithm for Fluorescence Molecular Tomography Imaging System[J]. Applied Optics, 2015, 54(32): 9573-9582.

[3]WANG K, WANG Q, LUO Q, et al. Fluorescence Molecular Tomography in the Second Near-infrared Window[J]. Optics Express, 2015, 23(10): 12669-12679.

[4]周源, 刘飞, 阮秋琦, 等. 基于荧光分子断层成像的多模成像系统研究进展[J]. 国际生物医学工程杂志, 2014, 37(1): 43-48.

ZHOU Yuan, LIU Fei, RUAN Qiuqi, et al. Research Progress in Multi-modality Imaging System Based Oil Fluorescence Molecular Tomography[J]. International Journal of Biomedical Engineering, 2014, 37(1): 43-48.

[5]BAI J, XU Z. Fluorescence Molecular Tomography[M]. Molecular Imaging Fundamentals and Applications. Heidelberg: Springer, 2012: 185-216.

[6]LIAN L C, DENG Y, XIE W, et al. Enhancement of the Localization and Quantitative Performance of Fluorescence Molecular Tomography by Using Linear nBorn Method[J]. Optics Express, 2017, 25(3): 2063-2079.

[7]ZHOU Y, GUANG H , PU H, et al. Unmixing Multiple Adjacent Fluorescent Targets with Multispectral Excited Fluorescence Molecular Tomography[J]. Applied Optics, 2016, 55(18): 4843-4849.

[8]LIAN L C, DENG Y, XIE W, et al. Enhancement of the Localization and Quantitative Performance of Fluorescence Molecular Tomography by Using Linear nBorn Method[J]. Optics Express, 2017, 25(3): 2063-2079.

[9]JIANG S, LIU J, AN Y, et al. Novel l 2, 1-norm Optimization Method for Fluorescence Molecular Tomography Reconstruction[J]. Biomedical Optics Express, 2016, 7(6): 2342-2359.

[10]程璟星, 侯榆青, 董芳, 等. 稀疏正则和自适应有限元的荧光分子断层成像[J]. 西安电子科技大学学报, 2015, 42(2): 174-179.

CHENG Jingxing, HOU Yuqing, DONG Fang, et al. Fluorescence Molecular Tomography Based on the Sparse Regularization and Adaptive Finite Element Method[J]. Journal of Xidian University, 2015, 42(2): 174-179.

[11]HE X W, LIANG J, WANG X, et al. Sparse Reconstruction for Quantitative Bioluminescence Tomography Based on the Incomplete Variables Truncated Conjugate Gradient Method[J]. Optics Express, 2010, 18(24): 24825-24841.

[12]张旭, 易黄建, 侯榆青, 等. 基于局部保留投影的荧光分子断层成像快速重建[J]. 光学学报, 2016, 36(7): 213-222.

ZHANG Xu, YI Huangjian, HOU Yuqing, et al. Fast Reconstruction in Fluorescence Molecular Tomography Based on Locality Preserving Projections[J]. Acta Optica Sinica, 2016, 36(7): 213-222.

[13]YAO R, PIAN Q, YAO R, et al. Wide-field Fluorescence Molecular Tomography with Compressive Sensing Based Preconditioning[J]. Biomedical Optics Express, 2015, 6(12): 4887-4898.

[14]AN Y, LIU J, ZHANG G, et al. A Novel Region Reconstruction Method for Fluorescence Molecular Tomography[J]. IEEE Transactions on Biomedical Engineering , 2015, 62(7): 1818-1826.