基于博弈论与可拓学的非正常接发列车人因风险评价*

郑云水，康毅军，牛行通

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

0　引言

铁路非正常条件下的接发列车作业是行车组织中重要的工作环节之一。目前，我国铁路各个车站的接发列车作业安全系数在各方面都有较大幅度的提高，然而，当系统处于设备故障、自然灾害、不良天气等非正常条件下，工作人员受知识经验、工作应力、应急演练不足等因素的影响，在这种非正常的情况下发生人因失误的概率比正常条件下显著增加[1-2]。为此，许多学者开始着重于人因失误的定性与定量研究，进行人的可靠性研究分析(HRA，Human Reliability Analysis)，以期找出导致人因事故的主要原因，并采取有效措施，尽可能从源头上减少人因差错，且有利于知识经验的学习以及数据的收集。同时，在人因失误概率分析与评价中，正确地考虑人因差错及其概率的定量化十分重要，它不但可以揭示系统的薄弱环节，从而有针对性地对系统设计进行改善或者采取一定的防护措施；更能够进一步通过评估这些防范措施的有效性，来确认措施对人因差错风险的影响，从而减少或削弱系统功能的危害性[3-4]。因此，如何更加科学地对铁路非正常条件下接发列车作业人因风险进行分析与评价，对当前铁路发展的意义重大。

目前，在铁路人因风险分析方面，国内外学者主要集中在人因差错事故的分析、接发列车的安全保障技术等方面。比如，MELISSA等人用HFACS (人的因素分析和分类系统) 分析多起铁路行车事故[5]；LUCA等人用贝叶斯网络和模糊专家系统2种方法对人的可靠性进行了详细分析[6]；国内吴海涛分析了非正常条件下高铁调度指挥人因可靠性，提出了一种改进的人因失误概率量化的方法[7]。从研究成果来看，接发列车作业人因可靠性分析仍然处在经验阶段，且在各种研究方法中，或多或少存在缺陷，如缺乏人因可靠性分析数据、数据量化存在片面影响而必须依靠专家的主观判断、人的认知行为很难量化等。因此，本文在非正常条件下接发列车作业认知行为的基础上建立多级可拓评价模型，利用博弈论的思想将由AHP法得出的主观权重与由熵值法得到的客观权重进行最优组合，克服了主观赋权法受人为主观影响较大与客观赋值法过度依赖客观数据而忽视专家经验的不足。此外，运用可拓学原理，建立非正常条件下接发列车作业人因风险多级可拓评价模型，该可拓评价法将评价标准从单一明确值转化为一个区间值，更加符合现实的应用，进而能够对非正常条件下接发列车作业人因风险进行有效分析。

1　非正常条件下接发列车作业认知过程分析

非正常条件下铁路接发列车作业是行车组织中的重要环节，其工作性质决定了作业人员要长时间集中精力，因而更容易发生人因事故。人因失误是由人的不安全行为所造成的，同时人的认知机理要受到行为形成因子(PSF, performance shaping factor)的影响。Wickens提出了1种认知行为机理四阶段模型，认为人的认知机理是由观察、解释、计划及执行构成的往复的信息处理过程；Rasmussen也提出了关于技巧、规则和知识相关的认知行为模型(SRK模型)[8]。在Wickens的认知模型中，用信息流的方式来分析外界信息的输入与输出之间的人的思维活动，缺点是对人的内部认知机制并未做出合理的分析与解释。因为SRK认知行为理论可为Wickens的认知机理提供有益的指导，所以本文将这2种模型结合，更加详细地解释情景环境因子对认知行为的影响。在结合非正常条件下铁路接发列车工作特征与工作人员的认知机理的基础上，构建如图1所示的认知行为模型。

图1　非正常情况下铁路接发列车认知行为模型Fig.1　The cognitive behavior model for arrival and departure of trains under abnormal conditions

2　非正常情况下接发列车作业人因风险评价指标体系及权重

2.1　建立评价指标体系集

为全面了解非正常情况下接发列车作业人因风险影响因子，对兰州铁路局接发列车作业人员进行了调研，在调研资料分析的基础上，运用图1所建立的认知行为模型，识别潜在的人因风险评价指标，以此建立非正常条件下接发列车作业人因风险评价指标体系，如图2所示。

图2　非正常条件下接发列车作业人员典型行为形成因子PSFs指标体系Fig.2　The main PSFs index system for arrival and departure of trains under abnormal conditions

进而建立非正常条件下接发列车作业人员行为形成因子PSFs指标集C={C1,C2,C3}，其中C1={C11,C12,C13}，C2={C21,C22,C23,C24}，C3={C31,C32,C33,C34}。

2.2　层次分析法确定指标权重

层次分析法(AHP, Analytic Hierarchy Process)是美国T.L.SAATY提出的为处理复杂问题的多准则思维和合理决策评价办法[9]。其基本步骤如下：

1) 建立构造判断矩阵

在层次分析法中，对同一层次不同指标按照重要程度赋值，准则是1至9标度，赋值如表1所示。

表1　重要程度赋值判断

根据专家组与统计数据合理地确定出各因素的相对重要性，得到判断矩阵为：

式中：aij=1/aji(i,j=1,2,…,n)。

2) 判断矩阵一致性检验

不同平分专家对通一系统认识角度的不同，以及主观判断的片面性等而出现矛盾不合理，因此需要对判断矩阵做一致性检验，表达式如下：

(1)

式中：CR为判断矩阵随机一致性比率；CI为一致性指标；RI为平均随机一致性指标。定义一致性指标CI=(λmax-n)/(n-1)；λmax为判断矩阵的最大特征值；n为判断矩阵的维数。当CR<0.1时，判断矩阵的不一致是满意的，否则需要对判断矩阵做修改再进行一致性检验。RI的取值如表2所示。

表2　随机一致性指标RI

3)计算指标的权重

对满足一致性检验的判断矩阵A进行归一化处理得到A'，接着对A'元素按行求和并进行归一化处理，得到特征向量ω，此特征向量即为该专家对应评价指标的权重。

2.3　熵权法确定指标权重

熵权计算法[10]运用数学方法确定各评价指标的重要程度。评价指标的熵权值越大，说明该指标可以提供越多的有用信息，对评价结果产生的影响作用越大。步骤如下：

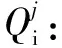
(2)

2) 确定指标j的熵值ej：

(3)

3) 确定指标j的熵权值ωj：

(4)

2.4　博弈论确定指标综合权重

由于人因风险受多种因素影响，且各种因素的影响程度不同，因此各因素不同的权重分配对评价结果的准确性影响甚大。在AHP主观赋权法中，它或是存在较大的主观因素，或是没有考虑指标本身对问题的重要性差异。然而在实际评价问题中，指标因素的重要程度不受决策者主观因素的影响，是客观存在的，只有将主、客观权重综合，才能反映评价指标的重要程度。因此，本文采用博弈论中的纳什均衡[11]，使主观权重与客观权重在竞争中寻找一种最优化的策略组合，使得每个指标的取值是对其它指标取值的最优反应，缩小主、客观权重两者与可能的权重之间的偏差，从而得到人因风险评价指标的综合权重。这种方法既体现了主、客观权重确定方法既相互竞争，又协调一致的思想，能够客观、合理、科学地解决权重的问题，并且能够克服传统可拓评价中忽略评价指标本身对评价结果重要性影响的缺陷。

假设由AHP法得到的指标权重为ω1，由熵权法得到的指标权重为ω2，则可以构造由这2个权重组成的向量集ω={ω1,ω2}，这2个向量的任意线性组合可表示为：

(5)

式中：λi>0为线性组合系数，i=1,2。

根据博弈论思想寻找一组合适的λi使ωi与ω之间离差最小，即：

(6)

由矩阵的微分性质知其最优化一阶导数条件为：

(7)

用Matlab求得(λ1,λ2)，对其进行归一化处理可得：

(8)

故指标的综合权重为：

(9)

3　建立多级可拓模型

3.1　确定安全风险等级集

根据我国铁路安全风险管理相关规定[12-14]，建立非正常条件下接发列车作业人因风险等级集N={N1,N2,N3,N4}，见表3。

表3　非正常条件下接发列车作业人因风险等级定义

3.2　确定各评价指标关于风险等级的关联度

根据可拓学原理采用关联函数来表达待评指标具有的某种性质的程度大小，它是表征事物质变及量变的量化方法[15-16]。因此，通过对关联函数的计算，我们可以得到各评价指标对于各类别的等级关联度。

1)初等关联函数

当T0=，T=，T0∈T，且两者有公共端点时，D(t,T0,T)=ρ(t,T)-ρ(t,T0)=0，因此有：

2)区间型初等关联函数

①T=，且最优值在中点t′=(a+b)/2处取到时：

(10)

②T=，且最优值在t′=a处取到时：

(11)

③T=，且最优值在t′=b处取到时：

(12)

3.3　安全风险评价

各指标关于各风险等级的综合关联度为：

(13)

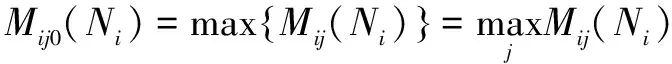
(14)

4　非正常条件下接发列车作业人因风险评价实例分析

对于非正常条件下铁路接发列车作业，运用上述多级可拓评价法可对其人因风险进行综合评价。通过对兰州铁路局骆驼巷站非正常条件下接发列车作业现场数据进行搜集与现场调研，采用专家打分的方法采集数据，为保证可靠性，邀请不少于10位接发列车作业专家，每位专家都必须对接发列车作业有深入的了解，根据表3风险等级的定义对所建立的非正常条件下接发列车人因风险评价指标进行打分，以100分为满分，得到其各单项指标的风险评价值如下：

{C11=96,C12=93,C13=98}{C21=91,C22=88,C23=93,C24=97}{C31=89,C32=96,C33=97,C34=93}。

下面以“工作人员与班组合作交流风险C2”为例进行风险评价。

4.1　指标权重计算

1) 基于AHP法确定主观权重

根据铁路非正常条件下接发列车作业专家结合现场实际情况，确定“工作人员与班组合作交流风险C2”二级指标相对重要程度，这里给出由4位铁路接发列车作业专家构造的判断矩阵：

用MATLAB求得该判断矩阵A最大特征值λmax=4.175 2，由式(1)得其判断矩阵A的随机一致性比率CR=0.065<0.1，即满足一致性检查；接着通过AHP法步骤3计算得到各指标权重为：

ω21=0.207,ω22=0.464,ω23=0.233,ω24=0.096。

2) 基于熵权法确定客观权重

同样结合4位专家根据非正常情况下接发列车的实际情况，对“工作人员与班组合作交流风险C2”二级指标进行打分(满分5分)，最终确定决策初始判定矩阵X为：

根据公式(2)～(4)提出的熵权计算法用MATLAB得到每个二级指标的熵权值为：

ω21=0.248 3,ω22=0.044 5,ω23=0.317 9,ω24=0.389 3。

3) 基于博弈论思想确定综合权重

根据式(5)～(9)可得“工作人员与班组合作交流风险C2”二级指标综合权重为：

ω21=0.241 8,ω22=0.329 4,ω23=0.286 2,ω24=0.142 6。

4.2　确定指标关于各风险等级的关联度

对于表3中N1级风险等级，分值越低，则隶属于该风险等级的隶属度越大，所以选择式(11)最优点在左侧的关联函数计算各指标关于该等级的关联度，则该式中，a=0，b=79。

对于表3中N2级、N3级风险等级，分值在区间中间时，隶属于该风险等级的隶属度最大，所以选择式(10)最优点在区间中点的关联函数计算各指标关于该等级的关联度，对于N2级，a=80，b=89；对于N3级，a=90，b=95。

对于表3中N4级风险等级，分值越高，则隶属于该风险等级的隶属度越大，所以选择式(12)最优点在右侧的关联函数计算各指标关于该等级的关联度，则该式中，a=96，b=100。

以“工作人员与班组合作交流风险C2”中“工作负荷状况C21”风险为例计算其风险等级的关联度：

同理可求得“工作人员与班组合作交流风险C2”中其他指标的风险等级关联度，如表4所示。

表4　C2评价指标关于各评价等级的关联度

4.3　安全风险评价

由表4单指标关联度与式(13)、式(14)可求得工作人员与班组合作交流风险(C2)关于各风险等级的综合关联度为：

同理可得工作环境风险(C1)及组织管理风险(C3)与各等级的综合关联度及等级特征值，如表5所示。

表5　评价指标与各等级的综合关联度及等级特征值

由表5可以看出，工作环境风险(C1) 与组织管理风险(C3)都属于N4级，安全风险水平较低，只需定期分析即可；工作人员与班组合作交流风险(C2)属于N3级，安全风险水平低，可以接受但不理想；另外由等级特征值可以看出C1与C3都偏向N3级，C2偏向N2级，有效修正了风险评价的偏差，提高了评价结果的准确性。从现场实际情况来看，该评价结果基本符合非正常条件下接发列车人因风险实际情况。

5　结论

1) 在充分掌握非正常条件下铁路接发列车作业的基础上，辨识潜在的人因风险，以此建立非正常条件下接发列车作业人员行为形成因子PSFs评估指标体系。

2) 构建的非正常条件下接发列车认知行为模型能够较客观、科学地辨识出人因风险，对于采取合理措施降低人因风险具有重要的应用价值。

3) 通过实例分析得到人因风险等级水平与等级偏向程度，评价结果与实际情况基本一致，为安全风险控制提供依据。采用博弈论思想对主、客观权重进行最优组合，避免了单一使用赋权法的不足，使评价结果更加科学与详细。

[1]吴海涛, 庄河. 一种基于认知过程分析的人因失误辨识方法-应用于高速铁路铁车调度系统[J]. 中国安全生产科学技术, 2014, 10(2):99-105.

WU Haitao, ZHUANG He. A Method of human error detection based on cogni-tive process analysis-application to high speed railway train dispatching system[J]. Science and Technology of Safety Production in China, 2014, 10(2):99-105.

[2]宋宏芳, 王天亮, 岳祖润, 等. 寒区铁路站场路基服役性能评价与分析[J]. 北京交通大学学报, 2017, 41(1):20-27.

SONG Hongfang, WANG Tianliang, YUE Zurun, et al. Evaluation and analysis of service performance of railway yard subgrade in cold regions[J]. Journal of Beijing Jiaotong University, 2017, 41(1):20-27.

[3]王波, 何世伟, 焦文根, 等. 铁路车务系统安全心里和行为模式的探讨[J]. 铁道运输与经济, 2016, 38(1):63-67.

WANG Bo, HE Shiwei, JIAO Wengen, et al. Discussion on safety mentality and behavioral patterns of train crew system[J]. Railway Transport And Economy, 2016, 38(1):63-67.

[4]JIN W, SHI Z, SIEGEL D, et al. Development and evaluation of health monitoring techniques for railway point machines[C]//Austin, 2015.

[5]MELISSA T. Understanding the human factor contribution to railway accident and incident in Australia[J]. Accident Analysis and Prevention, 2010, 40(17):50-57.

[6]LUCA P, PIERO B. Comparing the treatment of uncertainty in Bayesian networks and fuzzy expert systems used for a human reliability analysis application[J]. Reliability Engineering and System Safety, 2015, 138(2):176-193.

[7]吴海涛. 非正常条件下高铁列车调度指挥人因可靠性研究[D]. 成都: 西南交通大学, 2014.

[8]王黎静, 王彦龙. 人的可靠性分析-人因差错风险评估与控制[M]. 北京: 航空工业出版社, 2015.

[9]邓雪, 李家铭, 曾浩健, 等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2012, 42(7):93-100.

DENG Xue, LI Jiaming, ZENG Haojian, et al. Research on computation methods of ahp wight vector and its applications[J]. Mathematics in Practice and Theory, 2012, 42(7):93-100.

[10]罗毅, 李昱龙. 基于熵权法和灰色关联分析法的输电网规划方案综合决策[J]. 电网技术, 2013, 37(1):77-81.

LUO Yi, LI Yulong. Comprehensive decision-making of transmission network plan-ning based on entropy weight and grey relational analysis[J]. Power System Technology, 2013, 37(1): 77-81.

[11]赵文会, 闫豪楠, 何威. 基于风火网非合作博弈的电力市场均衡模型[J]. 电网技术, 2017, 41(5): 1-8.

ZHAO Wenhui, YAN Haonan, HE Wei. Equilibrium model of electricity market based on non-cooperative game of wind farms, coal-fired power plants and power grid company[J]. Power System Technology, 2017, 41(5):1-8.

[12]吴海涛, 罗霞. 基于直觉三角模糊TOPSIS的高铁列车调度指挥人因失误风险排序[J]. 中国安全生产科学技术, 2014, 10(4):139-144.

WU Haitao, LUO Xia. Risk prioritization model of human error for high-speed railway dispatchers based on intuitionistic triangular fuzzy TOPSIS[J]. Journal of Safety Science and Technology, 2014, 10(4):139-144.

[13]潘科, 王洪德, 石剑云. 多级可拓评价方法在地铁运营安全评价中的应用[J]. 铁道学报, 2011, 33(5):14-19.

PAN Ke, WANG Hongde, SHI Jianyun. Application of multi-level extensible method to urban subway operation safety evaluation[J]. Journal of the China Railway Society, 2011, 33(5):14-19.

[14]谢红卫, 孙志强, 李欣欣, 等. 典型人因可靠性分析方法评述[J]. 国防科技大学学报, 2007, 29(2): 101-107.

XIE Hongwei, SUN Zhiqiang, LI Xinxin, et al. An overview of typical methods for human reliability analysis[J]. Journal of National University of Defense Technology, 2007, 29(2):101-107.

[15]OMER F E, FATIH C, UDAY K. Failure diagnostics on railway turnout systems using support vector machines[C]//Brighton, 2010.

[16]张亚东, 郭进, 戴贤春, 等. 基于多级可拓评价法的列车运行控制系统运营安全风险评价[J]. 中国铁道科学, 2013, 34(5):114-119.

ZHANG Yadong, GUO Jin, DAI Xianchun, et al. Operation safety risk evaluation of train control system based on multilevel extensible evaluation method[J]. China Railway Science, 2013, 34(5): 114-119.