纯电动城市客车底盘车架的模态分析与优化

任可美，戴作强，郑莉莉，冷晓伟，李希超

（1.青岛大学机电工程学院，动力集成及储能系统工程技术中心，青岛 266071；2.中国科学院青岛生物能源与过程研究所，青岛 2661011）

0 引言

纯电动城市客车是新能源汽车的一种，在行驶过程中由于受到路面激励以及各种外部载荷激励等会产生振动。汽车振动不仅会影响操纵稳定性、乘客乘坐汽车的舒适性与稳定性[1,2]、引起共振等，还会严重影响汽车零部件的使用寿命。

汽车模态分析是研究汽车动力特性的重要手段，从事汽车结构研究工作的学者都会对汽车的模态进行大量分析。朱静等[3]结合数值模拟与振动台试验，分析了某车车体模态，提出将质量和刚度分开考虑的模拟方法；李真等[4]利用ABAQUS软件，对某客车进行模态分析，得到客车车架的前三十阶模态，并对车身动态性能进行了评价；Benatzky等[5]根据模态实验确定了地铁车辆的结构动力学特性；王若平等[6]将客车模型导入Hypermesh中划分网格，然后再借助MSC.NASTRAN对客车进行模态分析，得到前十阶模态，并根据分析结果予以评价；柯俊等[7]利用阶次跟踪法与模态分析相结合的方法，对轻型客车进行模态灵敏度分析及尺寸优化，有效的控制了客车地板的剧烈振动；陈龑等[8]针对某客车存在的共振问题，对车身进行模态分析，根据结果参数进行仿真分析，提出优化措施并改善白车身的NVH性能。本文针对某城市客车底盘车架，对其进行模态分析，将分析结果进行评价并结合分析结果对车架进行参数优化以达到轻量化目的。

1 纯电动城市客车的建模与简化

根据电动客车的二维图形在SolidWorks中建立客车三维模型，导出stp格式的模型，将模型导入SCDM软件中，对模型进行前处理。在SCDM软件中，删除简化模型中非承载件并根据梁的不同厚度抽取中间面。将抽取完中间面的模型导出导入到Hypermesh中。

2 纯电动客车的有限元模型处理

在Hypermesh中，耦合连接各零件，划分网格，设置单元及其属性，如图1所示。在Hypermesh中划分网格，网格尺寸为10mm，网格数量600109，节点数589727。检查网格质量，2D单元qualityindex质量为优占99.9%，雅克比系数均大于0.6。三角形网格最大内角小于120°，最小内角大于20°；四边形网格最大内角小于135°，最小内角大于45°，无重合网格，网格之间悉数缝合。在Hypermesh中，赋予网格单元PSHELL单元并根据不同零件的壳厚赋予厚度。车架材料为Q345，材料属性如表1所示。

表1 Q345材料参数

3 模态分析理论

汽车在行驶过程中，由于路面不平、发动机激励，传动系统以及车轮旋转等都会激起汽车的振动。研究汽车振动即是研究汽车模态，汽车每个模态具有特定固有频率、阻尼比和模态振型[9]。关于汽车的模态分析就是计算汽车结构振动特性的数值技术[10]，最终目的是得到汽车结构的模态参数，为汽车结构的振动特性分析、振动故障诊断与预报以及汽车结构动力特性的优化设计提供依据[11]。

将汽车看作是四自由度的振动模型，当车身质量分配系数ε的数值接近1时，前后车身系统的垂直振动几乎是独立的，此时可以将振动模型简化为两自由度振动系统，运动微分方程为[12]：

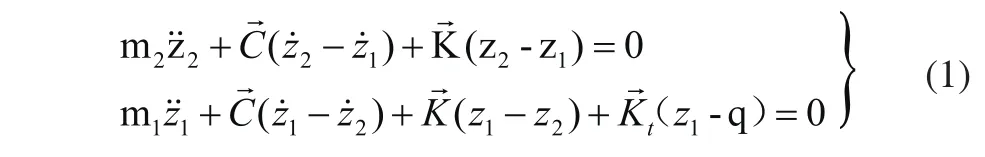
式(1)中m1表示非悬挂质量即车轮质量，m2表示悬挂质量即车身质量，z1表示车轮垂直位移，z2表示车身垂直位移，表示阻尼系数，表示弹簧刚度，表示轮胎刚度，q表示路面谱激励。

考虑无阻尼自由振动时，运动方程(1)变为：

这里的模态分析是基于底盘结构的自振动频率，即当车轮m1不动，则z1=0，可得：

4 底盘车架的模态分析

4.1 纯电动客车底盘车架模态分析结果

基于模态分析的理论基础，在HyperWorks中的Radioss求解器中进行车架的自振动模态分析。电动公交车车身结构的前6阶频率值均为0或接近于0。因此，可以判断电动公交车车架的前6阶模态为刚体模态[13]，代表的是车架的刚体位移。这6阶模态对进行振动分析并没有参考意义，因此在以下分析中不予讨论。过滤掉车架刚体模态，分析得到底盘车架的前十二阶固有频率，如表2所示。

表2 底盘车架自振动模态分析前12阶固有频率

模态分析中车架的实际振幅很小，将车架位移整体放大300倍，车架的固有振型，如图2所示。

图2 纯电动城市客车底盘车架振型

4.2 纯电动客车底盘车架模态分析结果分析

模态分析通过对纯电动城市客车底盘车架的前十二阶自振动模态分析可知：客车底盘车架的一阶振型为扭转，车架前段振幅较大；二阶振型为垂向弯曲，车架左侧中段与前段振幅较大；三阶振型为一阶侧向扭转，车架前段振幅较大；四阶振型为二阶扭转，车架前段振幅较大；五阶振型为一阶弯扭复合振型，左后轮桥振幅较大；六阶振型为二阶弯扭复合振型，左右后轮桥振幅均较大；七阶振型为垂向弯曲与局部振型组合，车架前段支架下支架振幅最大；八阶振型为局部振型，车架前段支架下支架振幅最大；九阶振型为弯曲扭转复合振型，车架中段振幅较大；十阶振型为局部振型与弯曲振型复合振型，车架前段支架上支架振幅最大；十一阶振型为局部振型，架前段支架下支架振幅最大；十二阶振型为局部振型，架前段支架第二根下支架振幅最大，总结如表3所示。

表3 各阶模态结果分析

4.3 纯电动客车底盘车架模态分析结果评价

客车在行驶过程中应该满足：车架的固有频率应该避开路面不平引起的振动[15]。已知客车在城市道路行驶过程中路面激振频率一般在1～3Hz之间，而城市客车传动轴的激励频率一般在30Hz左右[16]。由表2知该车第一阶模态频率为5.76Hz，大于路面激励；第八阶模态频率为31.90Hz，余传动轴激励频率极为接近，因此需进一步优化

5 基于模态分析与静强度纯电动客车底盘车架参数优化分析

5.1 优化设计理论基础

优化设计具有三个基本要素，即设计变量、目标函数与约束条件。设计变量（v1、v2，…，vn）是优化过程中发生改变而达到优化目的的变量；目标函数f（V）=f（v1，v2，…，vn）就是优化目的，是关于设计变量的函数；约束条件（gj（V）、hk（V）、…）是限制设计变量的条件：

目标函数：f（V）=f（v1，v2，…，vn）；

约束条件：gj（V）≤0 j=1，…，m；

hk（V）k=1，…，mh；

5.2 纯电动客车底盘车架参数化优化分析

结合模态分析结果以及车架静强度要求，对底盘车架进行参数化优化。利用Hypermesh软件中的Optistruct模块对底盘车架进行参数化优化。设计目标函数是质量最轻，约束函数为车架应力以及变形。设计变量为零件的厚度，本文针对部分壳厚为4mm，5mm，6mm以及11mm的搭接壳进行参数优化设计，主要是变形量小、应力小的左右两侧梁以及前后横梁。如图3所示，黑色件为变量Shell_4，绿色件为变量Shell_5，红色件为变量Shell_6，粉色件为变量Shell_8，蓝色件为变量Shell_11。已知模型在急转弯工况时的最大应力为180Mpa，最大变形为7.7mm，将应力约束的最大上限值定为195Mpa，最大变形量放宽到10mm。将底盘车架整体模态的第八阶模态频率设置为下线最小33Hz，第七阶上线最大27Hz，避开传动轴的激励频率。

图3 优化位置

迭代优化次数为八次，图4为迭代最后一步壳厚云图。优化前后底盘车架自振动模态分析前十二阶固有频率对比如表4所示。

图4 最后一步迭代壳厚云图

表4 优化前后底盘车架自振动模态分析前12阶固有频率对比

5.3 优化结果评价

对纯电动城市客车底盘基于模态分析结果与静强度要求参数化优化设计后，各阶模态由表3知，第一阶自振频率为6.092736×100Hz，第七阶自振频率为2.640886×101Hz，第八阶自振频率为3.345645×101Hz。第一阶自振频率大于路面激振频率1～3Hz，七阶与八阶自振频率也都避开了城市客车传动轴的激励频率30Hz，结果理想，相应的振型图如图5所示。优化计算前车架质量为2.2吨，优化后质量为2.068吨，减重6%。优化前后各设计变量数值对比如表5所示，对优化后车架典型工况进行静强度分析，结果如图6与图7所示，优化后满载弯曲工况最大应力为170Mpa，最大变形为5.70mm，急转弯工况最大应力为187Mpa，最大变形为6.70mm，均满足车架的强度要求，优化前后各参数对比如表6所示。

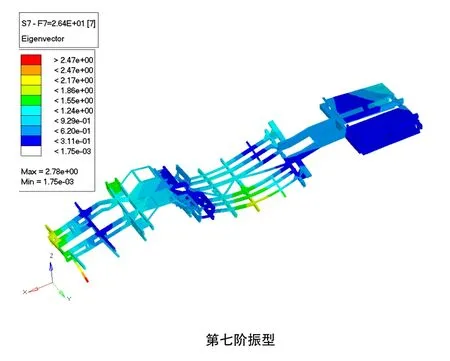
图5 优化后第七阶与第八阶振型

表5 优化前后各设计变量数值比较

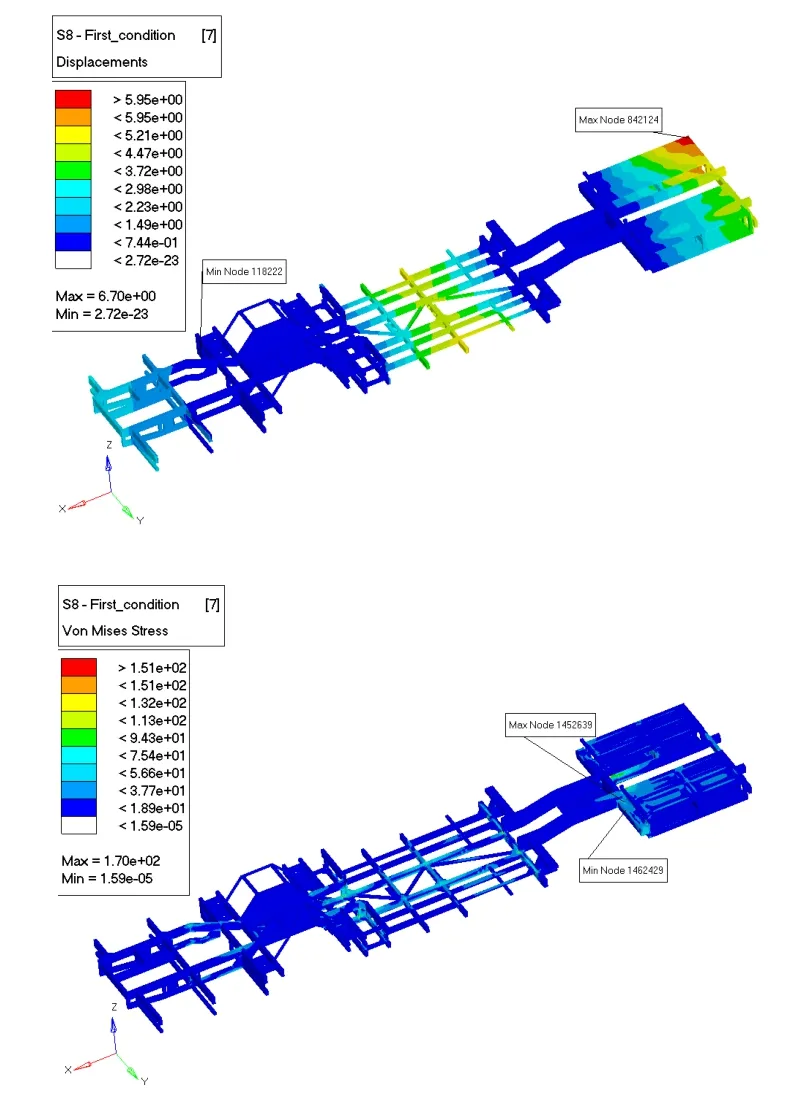
图6 优化后满载弯曲工况变形与应力

图7 优化后急转弯工况变形与应力

6 结论

本文分析了某纯电动城市客车底盘车架的自振动模态，并根据模态分析结果对车架进行参数化优化，将优化后的车架再次进行模态分析以及对优化后的车架进行静强度分析，分别得到车架的前十二阶模态、对应的固有频率、变形以及优化后底盘车架的应力与变形等。结果显示优化后的第一阶自振频率大于路面激振频率1～3Hz，第七阶与第八阶自振频率也都避开了城市客车传动轴的激励频率30Hz，结果理想。

优化后车架质量减轻6%，最大应力为187Mpa，最大变形为6.70mm。厚度为4.00mm的前轮过桥梁增至4.39mm；后段车载电池包上方纵向车架、后段车载电池包上方最后端横向车架、后轮过桥梁中间夹板、后轮过桥梁前支板以、车架前端横梁以及斜撑支架等由5.00mm减至3.50mm；前轮过桥梁两侧安装板由6.00mm减至4.50mm；后轮过桥梁由8.00mm增至9.00mm；车架前端搭接板由11.00mm减至8.00mm，这对以后生产加工该车底盘车架具有指导意义。

表6 优化前后各响应参数比较

【】【】

参考文献：

[1]高翔,赵清江,李阳,等.某微型客车车架模态及刚度的有限元分析[J].机械工程与自动化,2013(6):1-2.

[2]王锐,苏小平.汽车副车架强度模态分析及结构优化[J].机械设计与制造,2015(4):152-154.

[3]朱静,左言言,吴爽,等.轻型客车车身的有限元模态分析[J].噪声与振动控制,2005,25(2):23-25.

[4]李真,何锋,邹帆,等.基于ABAQUS的客车车身模态分析[J].汽车零部件,2013(1):57-59.

[5]Benatzky C, Bilik C, Kozek M, et al. Experimental modal analysis of a scaled car body for metro vehicles[J]. 2006.

[6]王若平,毛国威.基于MSC.NASTRAN的城市客车模态分析[J]. 重庆理工大学学报,2014,28(4):1-4.

[7]柯俊,陈志勇,史文库,等.基于振动控制的客车地板模态分析及结构优化[J].吉林大学学报(工),2015,45(3):719-725.

[8]陈龑,林建平,胡小舟,等.基于模态分析的某客车车身NVH性能优化[J].现代制造工程,2013(6):51-54.

[9]傅志方.模态分析理论与应用[M].上海交通大学出版社,2000.

[10]胡侃,戴作强,张铁柱.某混合动力城市客车车架结构模态分析与优化[J].青岛大学学报(工程技术版),2016,31(2):95-100.

[11]沈光烈,林圣存.基于有限元法的大型客车模态分析与结构改进[J].公路与汽运,2012(6):1-4.

[12]余志生.汽车理论[M].5版.机械工业出版社,2009.

[13]高翔,赵清江,李阳,等.某微型客车车架模态及刚度的有限元分析[J].机械工程与自动化,2013(6):1-2.

[14]王勇,孙备,李运,等.某重型载货汽车车架动态特性分析[J].机械与电子,2013(4):70-72.

[15]盛建,戴作强,张铁柱.纯电动客车车架结构模态分析与优化设计[J].制造业自动化,2015(15):44-47.