射电天文图像恢复的改进方法*
卫 明, 袁梅宇, 张秋明, 王 赟
(1.昆明理工大学 信息与自动化学院 ,云南 昆明 650000;2.阳泉市高新创业服务中心,山西 阳泉 045000)
0 引 言
目前,在射电天文图像重构算法中成熟的技术和方案大多采用洁化算法[1]和最大熵方法[2]作为核心思想的改进方法。洁化算法作为处理点源图像时恢复效果好于最大熵方法;而在处理展源时,最大熵方法优于洁化算法。很多天文图像处理软件包均采用这两种算法,但对于欠采样问题两者并未从根本上解决。
压缩感知理论是近年来由Candes,Romberg,Tao等人[3]新发表的关于信号处理的一种新的稀疏信号重构技术,在射电天文成像系统中对于采样函数是稀疏的。Donoho D L等人[4]曾多次将压缩感知技术应用于广域射电望远镜干涉成像之中,并用该方法解决了宇宙微波背景中的宇宙射线成像问题。为保证所成图像的精确度,本文使用日像仪天线接收太阳电磁波得到数据并对成像观测数据仿真,通过对输入图像傅里叶变换与对应位置相乘处理得到该图的频域数据,再经过傅里叶变换得到了模糊图像。 压缩感知的采样过程在稀疏域上进行,并且采样的点数很少;在重构方面,利用压缩感知理论中应用的最小范数,在大量实验中展示了其良好的效果。利用最大熵方法恢复了图像。本文方法取得了不错的天文图像恢复重构效果。
1 压缩感知基础理论
1.1 信号稀疏表示
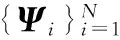
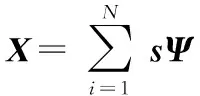
(1)

x为只有K个基向量的一个线性组合,并且满足K≪N。K为式(1)中si的非零个数,剩下的(N-K)个分量均为零。由于信号的稀疏特性,则式(1)中存在标准正交基 ,使得其系数只有很少的大系数和很多的小系数。可压缩的信号可以很好地被K稀疏信号逼近[8]。
获得全部的N长度的可压缩采样信号X;基于s=ΨTX,计算在完备集下的变换系数{si};确定K个大系数分量,丢弃(K-N)小系数;对K个大系数分量进行编码,并记录下该K个大系数分量的位置信息以便于重构信号。
这种采样然后压缩的构架模式本身存在着一些缺陷:1)采集到的数据长度N很大,但最终所确定的K个大系数数目可能会非常小;2)编码器必须计算出所有的N长度的变换系数{si},保留K个最大的,丢弃其余的;3)编码器不但要记录K个大系数,还要记录其位置信息。

y=ΦX=ΦΨs=Θs
(2)
式中Θ=ΦΨ为一个大小为M×N的矩阵。
观测过程是非自适应的,即观测矩阵Φ的选取与信号X不相关。
设计一个观测矩阵Φ和一个重构算法,要求:观测矩阵是一个稳定的矩阵,使得在信号降维过程中不会损失重要的信息;重构算法是从y=Θs中,在已知y和Θ的情况下找到满足y=Θs的最稀疏的s。
1.2 稳定观测矩阵设计
为解决已知K个非零值的问题。线性方程组M×N有唯一解的充分条件是:对于任意一个具有与s中K个非零元素完全相同的N维向量ν,满足
(3)
从式(3)中可以看出,矩阵Θ要必须要保证K稀疏向量的度量尺度长度在一定范围内变化。
在实际运用中并不清楚列向量s中K个非零元素的具体位置。然而,对于K稀疏或者可压缩信号有解的充分且必要的条件正是式(3),即约束等距条件(restricted isometry property,RIP)[9];另外,一种保证稳定性的方法是保证观测矩阵Φ和稀疏标准正交基Ψ是非相干的,即向量{φj}不能稀疏表示向量{ψj},反之亦然。
在压缩感知理论中,通常会为了避免关于选择具有约束等距条件的矩阵,而选择一个随机矩阵来作为观测矩阵Φ。如矩阵中每个元素φj,i均互相独立且遵循同一分布的随机变量(independent and identically distributed,IID),比如,观测矩阵Φ的元素均服从期望为0,方差为1/N的高斯分布[10],即可保证观测信号y是原始信号X的M个不同的随机加权的线性组合。另外,矩阵元素为±1的随机Rademacher矩阵也满足约束等距条件,具有普遍性[11]。
1.3 信号重构算法
为了在转换零空间中,找出原始信号的稀疏解向量s:
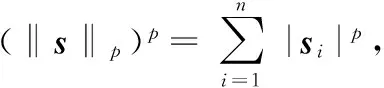
最小l2范数重构方法
(4)
由于式(4)中的l2范数不能反映出解的稀疏特性,因此,直观的思想在解向量中直接找到最稀疏的那组解,即最小l0范数
(5)
由式(5)中可以看出,只用M=K+1个高斯观测值,任意的优化解都能够高概率直接重构K稀疏信号[12]。但求解式(5)是一个不稳定,而且NP难问题。
2 最大熵原理
图像熵的定义有很多形式[13~16],其中,Frieden提出的形式主要用于天文图像上。熵最大时表示这些事件具有最大的不确定度,这在客观上要求事件是等概率分布,使图像的灰度趋于平滑,图像最大熵的恢复问题的公式表达为
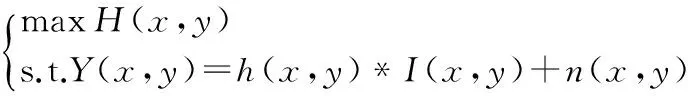
(6)
由图像熵的定义可知,I(x,y)不能为负,否则H(x,y)没有意义,因此,使图像最大熵作为判据,图像的正性将这个先验知识自然地得到了保证。
3 压缩感知与最大熵结合的图像恢复方法
3.1 最大熵方法
(7)

(8)
式中f(I)为I(x,y)的熵函数。对式(9)I(x,y)求导有
(9)
满足式(9)的解取代了式(7)的约束条件,获得了关于λ(x,y)的非线性等式。称函数J(x,y)为“带限”函数,通过式(9)能找到满足熵值最大的图像I(x,y),即
I(x,y)=f'-1[J(x,y)]≡g[J(x,y)]
(10)
熵函数的定义为f(I)=-IlnI,则g[J(x,y) ]=e(-1-J)。因此,图像函数I(x,y)即为一个关于“带限”函数J(x,y)的非线性函数。
3.2 最大熵方法与压缩感知相结合的方法理论
讨论一维熵函数
H=∑-xlnx
(11)
由函数-xlnx在x∈(0,1]区间的图像知曲线光滑,且在(0,+∞)区间内可导,在x=e-1时-xlnx达到最大值。
为了使函数满足凸函数,将熵函数变形为xlnx,求其导数为1+lnx,其在x∈(0,5]区间取值示意图如图1所示。图像中1+lnx只含有一个零点并且xlnx在零点左侧是减函数,零点右侧是增函数,因此,函数xlnx具有全局最小值。

图1 函数 1+lnx的曲线图像
用泰勒公式将xlnx展开在x0=0.4展开,有

(12)


图2 函数y与y1对比示意
取得区间为[0.01,1]步长为0.01的MATLAB仿真图。两曲线在该区间下的均方误差为0.053 7。求解最大熵就转换为了求解一个二次规划问题,即
(13)
因此,最大熵条件是作为一个目标函数,与压缩感知方法相结合后的目标函数变为
(14)
4 实 验
4.1 最大熵与压缩感知相结合方法实验
实验分为3幅不同的输入图片和3个不同的采样函数,即其效果和评价如图3和表1~表3,即采样函数为22条线,大型螺旋线、中心螺旋线,仿真实验结果分别为峰值信噪比(PSNR)和结构相似度(SSIM)。

表1 采样函数为22条线仿真实验结果

表2 采样函数为大型螺旋线实验结果

图3 采样函数为中心螺旋线仿真实验结果
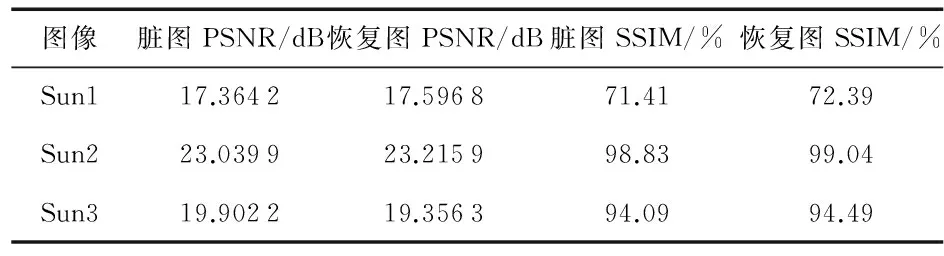
图像脏图PSNR/dB恢复图PSNR/dB脏图SSIM/%恢复图SSIM/%Sun117.364217.596871.4172.39Sun223.039923.215998.8399.04Sun319.902219.356394.0994.49
4.2 最大熵方法和最大熵与压缩感知结合方法对比
对于两种方法的对比结果如表4~表6。

表4 采样函数为22条线2种算法的恢复效果数据对比

表5 采样函数为大型螺旋线2种算法的恢复效果数据对比

表6 采样函数为中心螺旋线2种算法的恢复效果数据对比
4.3 实验结果分析
总体上看,用压缩感知和最大熵相结合的方法恢复图像的效果无论是PSNR还是SSIM上均较最大熵方法略胜一筹。不足之处在于,对于最后一组实验即183点中心螺旋线构成的采样函数中,sun1和sun3图像的PSNR和SSIM均较传统的最大熵恢复效果差,主要是因为采样点数太少,采样率为0.279 %,采样条件比较苛刻,另外,又由于采样点主要集中在零频附近几乎所有的采样点均为低频采样。
5 结 论
应用最大熵方法和压缩感知方法,对熵函数进行变换,用泰勒公式展开,化为二次型的形式,然后将这个二次型与稀疏解最小化作为目标函数,对图像进行恢复,对比实验数据,图像的效果有所提高,证明了方法的有效性。
参考文献:
[1] Monnier J D.An introduction to closure phases[C]∥Principles of Long Baseline Stellar Interferometry,2000:203.
[2] Högbom J A.Aperture synthesis with a non-regular distribution of interferometer baselines[J].Astronomy & Astrophysics Supplement,1974,15(15):417.
[3] Narayan R,Nityananda R.Maximum entropy image restoration in astronomy[J].Annual Review of Astronomy & Astrophysics,2003,24(1):127-170.
[4] Donoho D L.Compressed sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[5] Dimakis A G,Smarandache R,Vontobel P O.LDPC codes for compressed sensing[J].Mathematics,2011,58(5):3093-3114.
[6] Wenger S,Magnor M,Pihlström Y,et al.Sparse RI:A compressed sensing framework for aperture synthesis imaging in radio astronomy[J].Publications of the Astronomical Society of the Pacific,2010,122(897):1367-1374.
[7] Bajwa W U,Sayeed A,Nowak R.Compressed sensing of wireless channels in time,frequency,and space[C]∥Proc of 42nd Asilomar Conf Signals,System and Computers,Pacific Grove,CA,2008:2048-2052.
[8] 陈建明,张 彬.低功耗无线传感器能量供应装置的探索[J].传感器与微系统,2010,29(11):48-50.
[9] Wilson T L,Rohlfs K,Hüttemeister S.Tools of radio astronomy[M].Berlin:Springer,2009.
[10] 金 坚,谷源涛,梅顺良.压缩采样技术及其应用[J].电子与信息学报,2010,32(2):470-475.
[11] 张春花,刘方爱,申志远,等.一种新的异构无线传感器网络分簇算法[J].传感器与微系统,2013,32(6):143-146.
[12] Wiaux Y,Puy G,Boursier Y,et al.Spread spectrum for imaging techniques in radio interferometry[J].Monthly Notices of the Royal Astronomical Society,2009,400(2):1029-1038.
[13] Burg J P.Maximum entropy speetral analysis[C]∥Proc of the 37th Meeting of the Society of Exploration Geophysists,1967.
[14] Burg J P.A new analysis technique for time series data[C]∥Proc of the NATO Advanced Study Institute on Signal Proeessing with Emphasis on Underwater Aeousties,1965:12-23.
[15] Frieden B R.Rcstoring with maximum like lihood and maximum entropy[J].Journal of Optical Society of America,1972,62(3):511-518.
[16] Gull S F,Skilling J.Maximum entropy methods in image proces-sing[C]∥IEE Proc of Special Issue Commun Randar Signal Process,1984:842-850.

