基于四维超混沌系统观测器的语音通讯保密机制的研究

陈鹏飞，钱以迅

(苏州大学 文正学院，江苏 苏州215104)

0　引　言

随着信息科学和通讯技术的高速发展，以计算机为基础、国际互联网为载体的信息网络正在形成与完善。科学技术的进步和发展以及社会、军事、金融等各个领域都与信息通讯安全密不可分。安全、准确的信息已经成为当今社会的组织乃至于国家之间的沟通方式，保证传输处理不同信息的安全显得格外重要。

当加密数据量较大时，加密解密效率不高等弊端逐渐暴露，传统的信息保密技术的安全性已经不能完全满足需求，这时我们需要去寻找新的保密算法以确保通信系统的安全性。目前混沌理论是应用于通信保密机制的不二选择。所谓混沌，即确定性系统的随机行为的总称。混沌运动是非线性动力系统的一种特有运动形式。相对来说，四维超混沌系统含有两个正Lyapunov指数，将有更强的保密性和抗破译能力。然而对于超混沌系统来说，Lyapunov指数的计算迄今为止都是一个较难的问题[1]。我们利用超混沌系统进行语音通讯保密，相比于混沌系统具有更高的保密性能。

关于超混沌的研究，最早可以追溯到1979年，Rossler在Applied Mathematics上题为“Nonlinear oscillations in biology”的报告中首次提出超混沌的例子，并采用了“Hyperchaos”这一词语[2]。同年，Rosser在杂志Physics Letter A上给出了一个更简单的超混沌系统，该超混沌系统只具有一个二次非线性项的四维系统，其中包含的吸引子具有两个不稳定的方向，这个系统即为著名的Rosser超混沌系统[3]。

在连续自治系统中，超混沌产生条件为系统的维数至少是四维，其中超混沌吸引子在两个不同的方向上发生分离。在更高维的系统中，将允许超混沌吸引子在更多方向上发生分离，例如2010 年, K. H. Sun 利用参数扰动方法去控制一个 Lorenz 型系统, 从而获得了一个新的三维非自治超混沌系统[4]。基于一个非耗散的 Lorenz 型系统, Wei 提出并研究了一类只具有两个二次非线性项的无平衡点的四维超混沌系统[5]。

基于前人的研究成果，本文成功实现了将超混沌观测器的设计方法引入到语音通信保密机制的设计之中。首先，设计出超混沌的观测器，所得到的观测器结构简单且易于实现；其次，对所得到的观测器进行理论对比验证，并在Simulink中进行仿真验证；最后，利用所涉及的观测器算法，给出语音通信保密机制的设计方案。

1　研究的模型

超混沌系统具有复杂的非线性特征，下面简要阐述比较典型的两个超混沌系统。Lorenz系统如下：

(1)

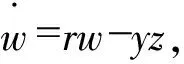
(2)

根据式(2)的方程可以设计几个参数来实现一个超混沌Lorenz系统的模型。

2　观测器设计

首先考虑如下的超混沌系统：

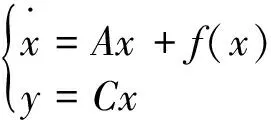
(3)

式中，x∈Rn,y∈R分别是系统的状态和输出。A∈Rn×n是一个常数矩阵，f:Rn→Rn是光滑的非线性函数。

现有如下的两个假设：

假设1.f(x)满足Lipschitz条件:

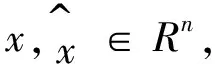
(4)

其中||·||表示欧几里得范数，γ>0。

假设2. 存在正定矩阵P∈Rn×n以及矩阵增益L∈Rn满足：

P(A-LC)+(A-LC)TP+γP2+γI<0

(5)

式中，I表示单位矩阵。

若假设1和假设2都成立，那么当前的系统(3)存在观测器，并且该观测器具有如下的形式：

(6)

3　加密和解密算法设计

本文所采用的加密和解密方式是在信息的发送方发送过信息之后语音信息即被加密，此处我们利用四维超混沌系统的状态作为加密机制。通过信道传输，然后在到达接受方之前，利用先前所设计出的观测器算法，通过增加一个“负”的信号，从而将原始信号从信道中还原出来。

由方程(1)可知，本文研究的超混沌系统可以由如下几组方程进行描述

(7)

式中，s是信息信号。则，基于状态观测器的接收器的设计如下：

以四维超混沌系统为基础并设计进行仿真验证，在Matlab中的Simulink进行模块的搭建，对加密解密的算法进行仿真验证。得出的原信号、加密信号和解密信号三者的对比图如图1所示。

图1　原信号、加密信号和解密信号对比图

最后将原信号与得出的解密信号作差，得到图2。

图2　原信号与解密信号作差

从图1、图2可以看出原信号与解密信号在经历了最初的不稳定因素扰动之后不断趋于稳定，与最初的实验预期基本吻合，可以精确的反映本套加密解密算法的稳定性和精确性。

4　结　论

本文以超混沌系统及其在语音通信保密机制上的应用提出了一套加密解密算法，并在Simulink上进行仿真验证。所实现的观测器不但能将原信号和解密信号对比，并且与混沌系统对比，其Lyapunov指数至少有两个正值，即保密性和抗破译能力更强，更能保障语音通信的保密。本文利用观测器从算法设计、仿真验证两个角度对该系统进行了验证。

参考文献：

[1]张学义，李殿璞.基于状态观测器的超混沌系统高精度同步方法[J].电路与系统学报，2001,6(4):15-19.

[2]R¨ossler O E. Chaotic oscillations-an example of hyperchaos, in: Nonlinear oscilla-tions in biology[R]. Lectures in Applied Mathematics, 1979, 17.

[3]R¨ossler O E. An equation for hyperchaos[J]. Physics Letters A, 1979, (71): 155-157.

[4]Sun K H, Liu X, Zhu C X,etal. Hyperchaos and hyperchaos control of thesinusoidally forced simplied Lorenz system [J]. Nonlinear Dynamics, 2012, 69(3):1383-1391.

[5]Wei Z C, Wang R R , Liu A P . A newnding of the existence of hidden hyper-chaotic attractors with no equilibria[J]. Mathematics and Computers in Simulation,2014, (100): 13-23.