粮食入仓自动分级现象PFC模拟及定量分析
原 方 李佳伟 崔秀琴 徐志军 张芝荣
(三明学院建筑工程学院;工程材料与结构加固福建省高等学校重点实验室1,三明 365004) (河南工业大学土木建筑学院2,郑州 450001)
粮食进仓发生自动分级现象[1-2]是储运过程中关注的现象之一,即混合的颗粒在流动时相似性质的颗粒趋向于聚集在一起,最后形成原混合物料中的不同大小的颗粒分离分层的状态。这种现象往往是颗粒在自由运动时自动产生并且不可避免的一种现象,大米成品粮入仓自动分级现象就是大米储藏面临的难题。它产生于大米入仓过程中,一旦分级严重并且得不到解决就会对大米存储期的品质和销售造成有害的影响。
我国粮仓建设比较广泛的有平房仓(主流仓型),浅圆仓和筒仓[3]等,其中筒仓具有便于机械化、自动化作业等特点。我国海南地区大量种植并加工稻谷,为满足企业生产需要,某设计研究院为生产企业设计了一种矩形筒仓并投入建设,该仓作为稻谷加工成大米成品粮到销售期间的储存仓。稻谷经过一系列的加工得到成品大米,此过程通常会造成一部分碎米籽,生产企业提供数据显示破碎率10%~15%。破碎后大米籽形状不规则,体积更小,摩擦系数变大。大米入仓采用在顶部定点垂直自由下落方式,如果不采取措施,就会不可避免地产生碎米和整籽粒米的自动分级现象[4]。
由于破碎大米粒径小,易受压变形等特点,聚集后空隙变小,通风能力下降,易升温、霉变。自动分级产生于粮仓的内部,现实中对分级形成过程和结果很难从外部进行探测,所以从理论上研究自动分级产生的原因和程度对改进粮食储藏工艺,为提高粮食存储品质提供参考。
1 自动分级现象的理论分析
散体物料的自动分级是一种普遍存在现象,混合颗粒物在运动或振动时非常容易发生分级。杨文生等[1]、王永昌[4]分析指出了分级主要发生在粮食在粮堆面上下滑的过程中。
首先分析单个颗粒的运动,实际中不同粮食颗粒的形状有差异,为了对散体颗粒的分级做一个普遍性的规律的预测,本实验把大米颗粒简化为球体颗粒(此处只考虑粒径和内摩擦系数两种因素的影响,没有考虑颗粒球形度),颗粒从仓顶自由下落,在仓底逐渐堆积出倾斜的粮堆面,当堆角大于颗粒休止角[4]时颗粒重力在斜面上的分量大于摩擦力,颗粒开始沿坡面滑落。颗粒到达斜面上时有初速度v0,此时颗粒下滑的摩擦系数是动摩擦系数,比静摩擦系数小30%,所以实际中颗粒在小于休止角的坡度就开始滑落。图1为粮粒的受力简图,设颗粒质量为m。则:
F=fFN=fGcosα
(1)
(2)
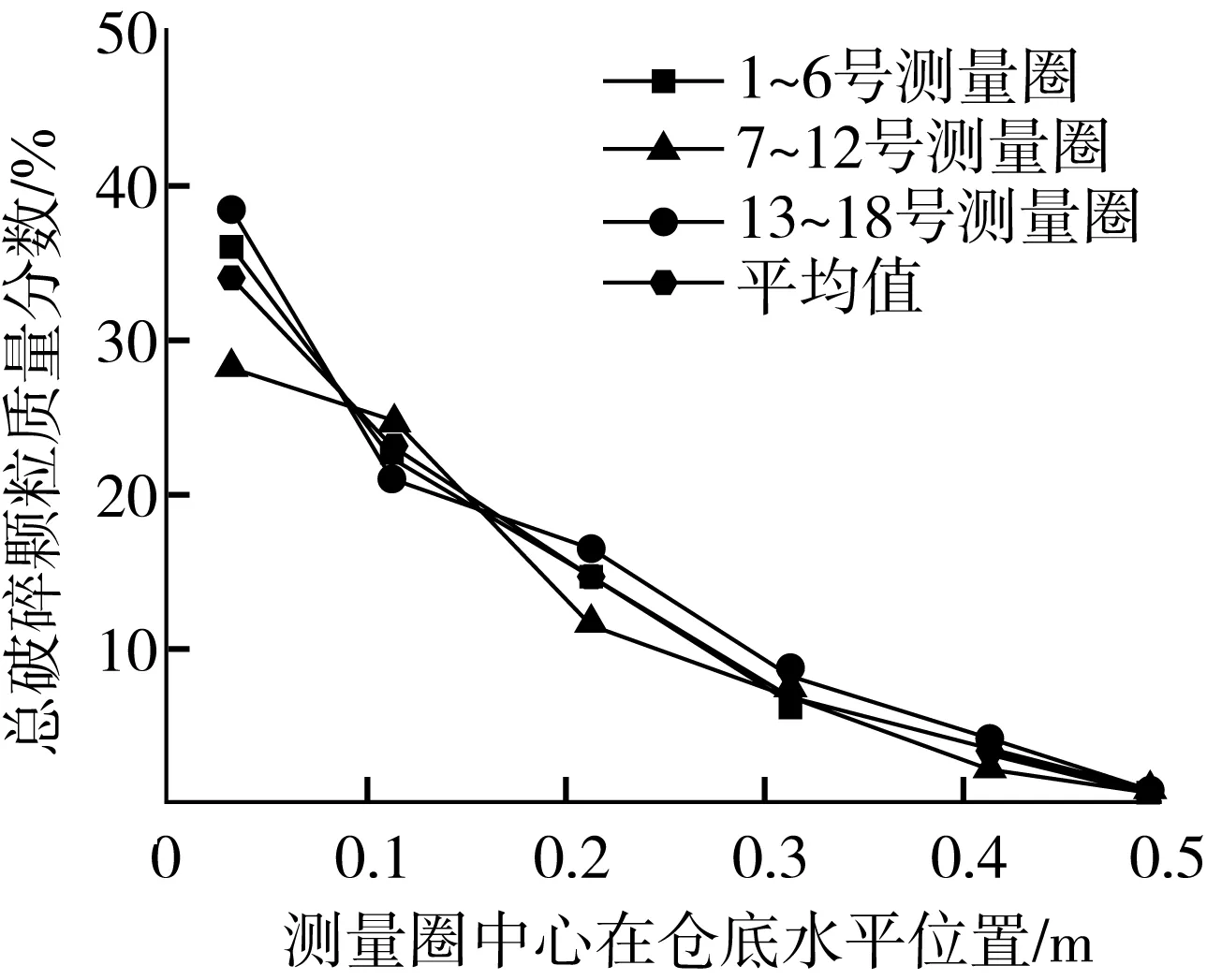
式中:G为重力/N;FN为粮面对颗粒支持力/N;F为摩擦力/N;f为摩擦系数;α为粮堆底角。当Gsinα>F时,颗粒加速下滑;当Gsinα 图1 颗粒在粮堆面的受力分析 颗粒在斜面上滑落的加速度与摩擦系数f和粮堆底角α有关,随着α角增大,完整颗粒先开始滑落,而且它的摩擦系数小,加速度更大。 休止角和摩擦因数小的颗粒先滑落且运动速度快;休止角和摩擦因数大的颗粒后滑落且运动速度慢,不同的颗粒沿着粮堆面滑落距离不同,最后形成分级。这仅是对单个颗粒在理想的平面上的运动分析,实际中颗粒数量庞大,粮堆表面不平整,颗粒在斜面上运动过程中相互作用复杂且不断变化,除了受摩擦力外还有其他颗粒的碰撞,接触力大小方向不断变化,难以进行统计和计算,所以理论分析结果与实际的分级存在不可预测的误差。 颗粒流[5-7]以离散单元法和牛顿第二定律为基础,能实现散粒体堆积运动过程中的相互作用,已经被多次用于筒仓和粮食的研究中,借助颗粒流模拟软件模拟分级过程有良好的理论依据和模拟基础。 颗粒流(PFC)[6]是用来模拟非连续介质的一种数值模拟软件。它以离散单元法为理论基础,主要模拟球体颗粒之间和球体与墙面之间的相互作用。颗粒流自出现以来主要被用于岩土、砂石和粉末等领域的研究中,由于它能够模拟散粒体堆积运动的特点,近些年来在粮仓内散料压力研究中得到了广泛的应用,并且得到了理想的结果。 原仓为钢筋混凝土矩形筒仓,水平截面为正方形,底部平分成9个漏斗作为出料口。仓体高9.5 m,长和宽均为4.8 m,漏斗高1.8 m,装粮高度达8 m。海南地区普通品种大米的参数为:重力密度8.5×105kN/m3,内摩擦角为30°。 模型筒仓为原仓缩尺10倍,形状与原仓保持一致,底部设置9个出料漏斗。仓高0.95 m,长和宽均为0.5 m,漏斗高0.18 m,模型如图2所示。 图2 模型仓 模型中的颗粒设置两种[7-8],在筒仓上部生成后自由落入筒仓。颗粒采用无规则随机分次生成,每次生成的两类颗粒基本均匀混合。第一种颗粒模拟完整的大米籽粒(由于程序本身的限制,模型中颗粒均为圆球形,只考虑了颗粒半径和内摩擦系数的大小),含量占总量的85%左右;第二种模拟破碎的大米,半径为大米的1/3~2/3,含量占总体15%左右。颗粒物理参数查阅有关规范后以实际大小赋值到颗粒模型中。 模拟仓为原仓缩尺后的模型,本实验模拟自动分级只考虑两类颗粒运动时相互作用,颗粒体对仓壁产生的应力和压力等不是分级的主要影响因素,不予考虑。因此颗粒重力密度取大米的原值,采用原重力密度使模拟更接近真实。模型仓中所需要的主要参数值见表1。 表1 各项主要模拟参数 注:Wall-kn表示墙体法向接触刚度;Wall-ks表示墙体切向接触刚度;Ball-kn表示两种不同颗粒的法向接触刚度;Ball-ks表示两种不同颗粒的切向接触刚度;Dens表示颗粒重力密度;Wall-for表示颗粒与墙体摩擦系数[9];Ball-for1表示完整颗粒摩擦系数;Ball-for2表示破碎颗粒摩擦系数。 模型中绿色颗粒(深色)为碎米颗粒,黄色(浅色)为完好大米颗粒,这样可以在装料中看出不同颗粒的运动状态。颗粒从筒仓顶部下落到仓底的过程中会发生碰撞,由于程序本身运算方式的特点,导致颗粒自由下落过程并不能与实际运动完全相同,颗粒碰撞后会获得动能,当到达一定大小后会向外崩散,为了防止颗粒向飞出,在模型中加了挡板装置,使模拟过程与实际情况尽量接近。挡板的作用只是约束了颗粒下落时不向外飞出,当颗粒到达粮堆面时不再与挡板接触,因此,不会影响颗粒分级。原仓装粮方式是由传送带送粮到仓顶后垂直落入仓底,颗粒入仓时无水平初速度。依据实际情况,模拟中颗粒水平速度为0,下落点选在仓左侧一角处。粮食垂直下落形成粮坡面,颗粒在坡面上是向外扩散运动的,不同方向上扩散基本相同,便于观察颗粒运动和分级状况,模拟给出了靠近外侧仓壁的颗粒运动。图2是模拟过程的6个阶段。 a 8×105时步 b 25×105时步 c 38×105时步 d 5×105时步 e 58×105时步 f 72×105时步图2 筒仓入料过程示意图 颗粒从左侧落入仓中,在仓底堆积后形成粮堆斜面,在重力作用下粮食颗粒沿斜面向下滑落至受力平衡后静止。为了使模拟中粮食下落更加接近颗粒实际自由落体运动规律,整个过程分为多次装粮,每次向仓内装入一定量的颗粒让颗粒在自重作用下下落并最终达到静力平衡,然后再开始泄入下一部分颗粒,这样反复进行数次,最后满仓后全部颗粒达到静力平衡[10]为止。 图3 静力平衡时仓内平均不平衡力变为零 模型运行时颗粒的总体平均不平衡力,反映了系统是否处于稳定平衡状态,由图3可以看出每一次装料后不平衡力都会有一个迅速的升高到一个值,然后逐渐降低为零,最后经过10次装料后,所有颗粒都达到静力平衡。 在模拟仓中靠近仓外侧仓壁处自下到上设置3行测量圈,测量圈是空心球体。每一排测量圈设置为与外侧仓壁平行,每一行从左到右排列6个,第一行从左往右编号为1~6;第二行为7~12;第三行为13~18,直径均为0.05m。图4为测量圈布置图。 图4 测量圈布置图 装料完成后监测圈内的平均孔隙率,然后删除全部的完整颗粒后再监测每个测量圈的平均孔隙率,通过两组孔隙率之间的差值和数量关系计算出圈内两种颗粒的含量比例。设测量圈的体积为1,则: V=1-P (3) V1=1-P1 (4) (5) 式中:V为测量圈中颗粒总体积;P为测量圈中孔隙率;V1为测量圈中破碎颗粒体积;P1为测量圈中删除完整颗粒后孔隙率;W为测量圈中破碎颗粒含有率。 计算得出含量变化曲线图,图表中横轴坐标表示测量圈中心在仓底的水平投影位置。图5为3行测量圈内破碎颗粒占总量的百分比曲线以及3行测量圈平均值曲线。 图5 测量圈内破碎颗粒含量以及平均值 从图5中破碎颗粒含量分布可以看出从落料点到粮仓右侧,破碎颗粒的含量逐渐减少。横坐标0~0.3 m之间曲线下降稍快,0.3~0.5 m之间下降稍慢,距离落料点越近减少速度越大,距离右侧仓壁处破碎颗粒含量几乎为零。 竖向上每列3个测圈内的破碎颗粒含量相差不大,即同一水平位置不同高度处的破碎颗粒含量基本相同,即水平位置一定时,竖直方向上颗粒不产生分级。 模拟显示粮食入仓的过程中会产生自动分级现象。分级发生在颗粒沿堆积斜面滑落阶段。两种颗粒在运动过程中发生位移差最终形成分级现象。 颗粒含量曲线表明:水平方向上从粮仓的落料一侧到另一侧小颗粒含量逐渐降低,呈现分级状态;竖直方向上破碎颗粒含量基本相同,不发生分级。 本实验借助PFC3D模拟自动分级现象,发挥了软件模拟颗粒堆积运动的特点,能观察粒子入仓分级的运动过程,并使分级程度得到定量表示。采用颗粒流方法研究自动分级仍处于探索阶段,由于软件本身的限制,模型仓为原仓缩尺,颗粒为圆形,随着技术的发展期望可以对更接近实际的仓和颗粒进行研究,得到更准确的结果。 [1]杨文生,张中,张成. 浅圆仓储粮自动分级研究现状[J]. 粮食加工,2011(5):74-76 YANG W S, ZHANG Z, ZHANG C. Research on automatic segregation of grain storage in shallow circular storage [J]. Grain Processing, 2011(5):74-76 [2]张来林,张爱强,朱彦,等.粮食自动分级的类型与预防措 施[J]. 粮食流通技术,2008(6):28-30 ZHANG L L, ZHANG A Q, et al.Types and preventive measures of automatic grain classification [J].GrainCirculation Technology, 2008(6):28-30 [3]李伟,霍印君,王晓丽,等.平房仓、浅圆仓和立筒仓储粮性能探讨[J]. 粮食储藏, 2006(5): 33-35 LI W, HUO Y J, WANG X L, et al. Discussion on the storage performance of [J]. Grain Gtorage, 2006 (5): 33-35 [4]王永昌. 浅圆仓粮食自动分级问题的讨论[J]. 粮食与饲料工业,2002(12):11-13 WANG Y C. Discussion on the automatic segregation of grain in the shallow round bin [J]. Grain and Feed Industry, 2002(12):11-13 [5]Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 2015, 30(30):331-336. [6]杜明芳,张昭,周健. 筒仓压力及其流态的颗粒流数值模拟[J]. 特种结构,2004(4):39-41 DU M F, ZHANG Z, ZHOU J. Numerical simulation of particle flow in silo pressure and its flow patterns, [J]. Special Structure, 2004(4):39-41 [7]Fang Yuan, Chengying Dong, Yaohui Song, et al. Particle Flow Simulation for Large Diameter Squat Silos Eccentric Discharge[J].Applied Mechanics and Materials,2011(99-100):1106-1112 [8]周健, 池永,池毓蔚,等. 颗粒流方法及PFC2D程序[J].岩土力学, 2000(3): 271-274 ZHOU J, CHI Y,CHI Y W, et al.Particle flow method and PFC2D program[J]. Geotechnical Mechanics, 2000(3): 271-274 [9]王伟,刘焜,焦明华,等. 颗粒物质摩擦因数对颗粒流润滑影响的仿真分析[J]. 中国机械工程,2009,20(7):856-860 WANG W, LIU K, JIAO M H, et al. Particles flow lubrication friction factor influence on the particle simulation of [J]. China Mechanical Engineering, 2009,20(7):856-860. PFC Simulation and Quantitative Analysis of Automatic Gradation of Grain Warehousing Yuan Fang1Li Jiawei2Cui Xiuqin1,2Xu Zhijun2Zhang Zhirong2 (School of Architecture and Engineering, Sanming University; Key Laboratory of Engineering Material and Structure Reinforcement of Fujian Province1, Sanming365004) (School of Civil Engineering, Henan University of Technology2, Zhengzhou450001)
2 离散单元法(PFC3D)数值模拟
2.1 原仓尺寸和数值模型建立
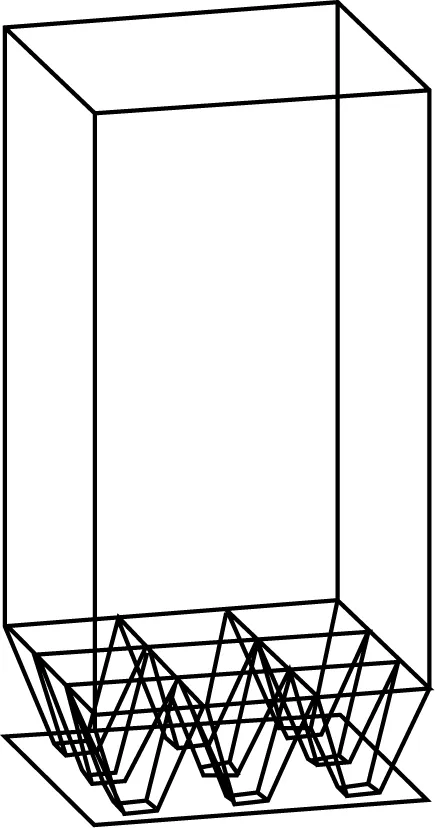

2.2 装料过程模拟

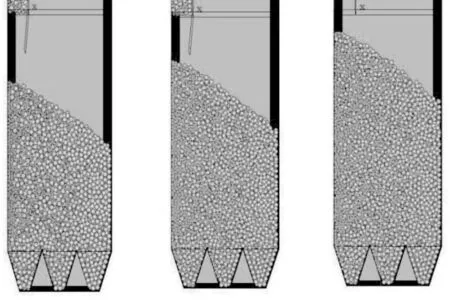
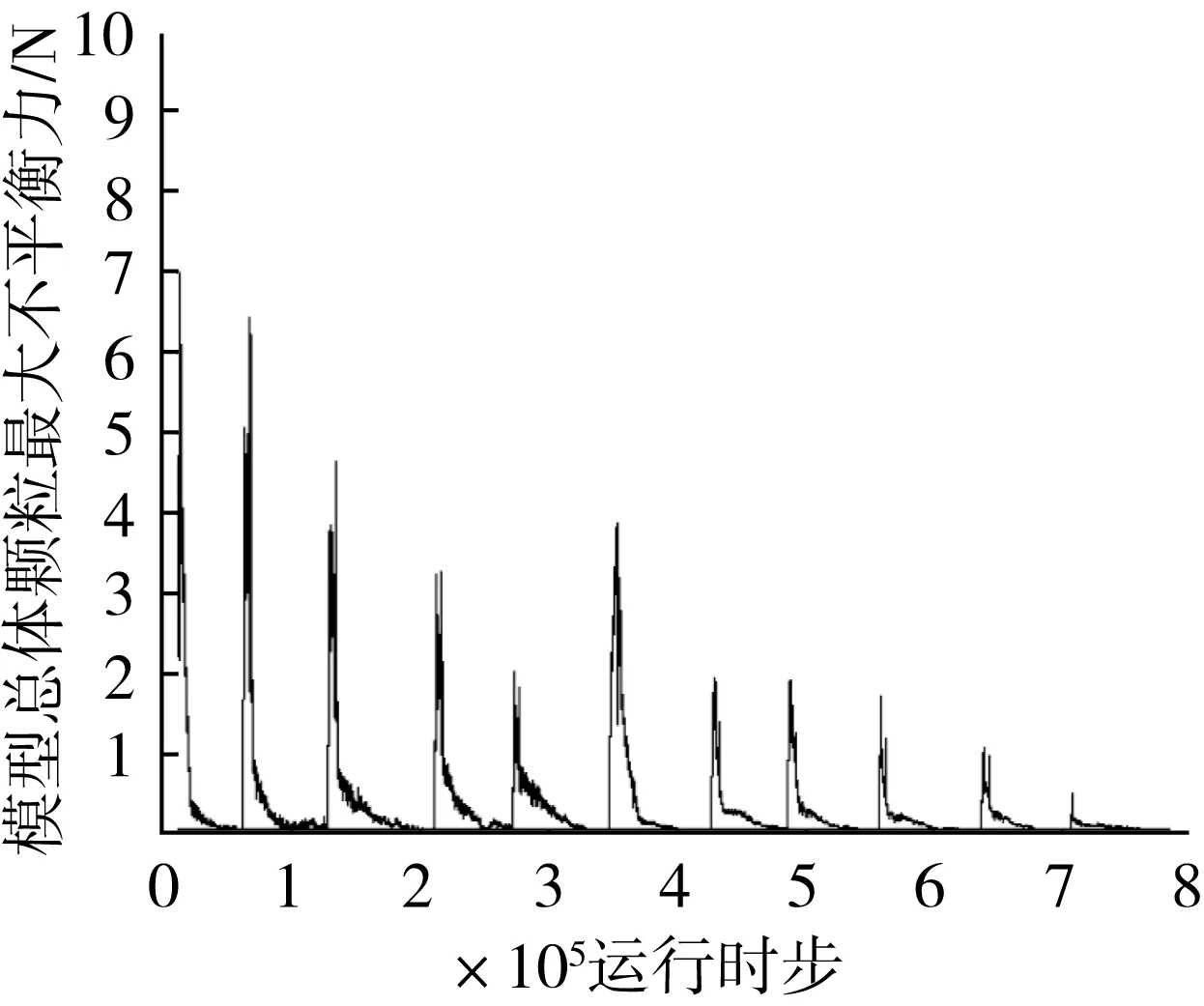
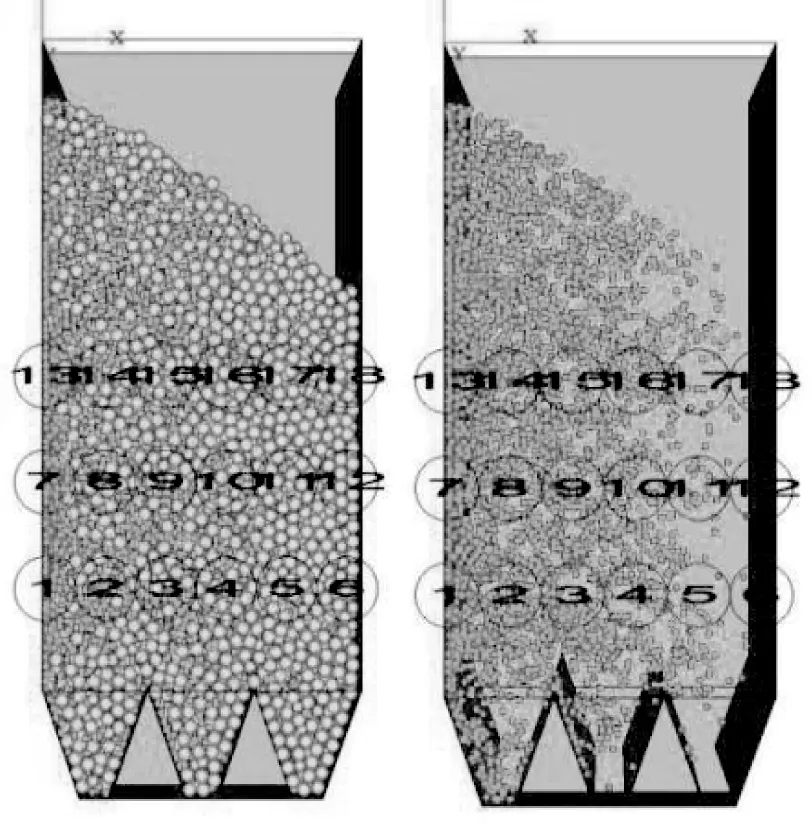
2.3 模拟结果与分析
3 结论

