循着问题的台阶“且问且行”——基于《求瓶子的容积》一课教学的思考

梁　燕　唐惠良

在人教版教材中，解决问题是教师关注与讨论的热点，从对方法的教学到策略的理解乃至数学思想方法的渗透，都是教学研讨的聚焦点。“求瓶子的容积”这个例题是在学生学习了“圆柱的体积”之后安排解决的“非常规”问题。面对这样一个新教学内容，我们带着诸多问题进行了思考。

一、设计问题的台阶，教学目标凸显什么

“求瓶子的容积”这一“非常规”问题，学生经验体系里是否有“瓶子倒置”的想法？对于在“瓶子倒置”之后，还能继续怎样思考？带着这样的问题，我们分析了教材的例题，同时也检索了不同版本的设计、杂志上的文章等，使我们对教材的意图与教学的目标逐渐清晰起来。从众多文章中梳理，我们发现许多教师侧重在引导学生观察思考中体会变与不变、转化、推理的数学思想。我们更倾向于“非常规”的问题不以计算为目的，我们认为这和其他的以数量关系为基础的解决问题属于不同地位，虽然策略特殊，但是它在经历解决问题的整个过程中培养学生“四能”的价值更明显：问题在哪里？可以提出什么问题？怎样设计解决问题方案？怎样回顾反思？……这些都体现了让学生经历问题解决的进程，这对学生解决不完整圆柱的容积问题乃至更为“非常规”的解决问题能力发展起着至关重要的作用。因此我们在教学中有意识地关注，一方面要与解决问题的一般过程和方法建立起联系，同时又要在具体问题解决的进程与台阶中，将特殊的解决问题的经验与能力适度提炼，化为一般的思想方法或思维模式。

基于以上思考和分析，我们对教学目标的定位体现在本节课的两个挑战性问题上：1.不借助其他任何容器，你们还有办法求出瓶子的容积吗？（设计方案）2.水的体积（圆柱体）加上空气的体积就是瓶子的容积了吗？为什么？

本节课使学生认识到之前的解决问题方法需要改进，改进为解决问题的方案，让方案设计变为学习的需要。我们把“问题解决”看成一种创造性的活动，即在问题解决的过程中，学生尝试寻找答案时，不是简单地利用已知信息，而是对信息进行加工，重新组织若干已知的规则，形成新的高级规则，这些活动涉及到了“高级”的思考过程,学生应在解决问题中，找出对当前问题适用的对策，这便形成了对“策略”的需求。

二、发现并提出问题，材料怎样设计

不同的教材都向学生展示了正放与倒放的图示，用意何在？我们想不能仅仅是让学生读懂教材呈现的两种状态，因为这不能很好地呈现伴随思考的过程。所以在材料设计时采用想象的方式，不过早呈现结果状态，而是以挑战性任务呈现，更有利于学生发现问题与提出假设。

师：（出示一个装满水的瓶子）你会想到什么？

生：计算体积可把水倒入一个量杯中，看刻度。

师：还有办法求出瓶子的容积吗？如何在没有量杯的情况下也能测出容积呢？

师：（教师现场喝掉一部分水，引导学生思考）现在你们有想法了吗？愿不愿意接受这个挑战？

【思考：随着问题提出去解决不断产生的新问题，这是“解决问题”教学的最佳状态，即以问题驱动学习。以“求一个装满水的瓶子的容积”问题驱动，直面任务，使得问题更加开放。同时在学生已有经验的基础上，在探究解决问题策略多样化的同时，引发学生思考，材料的动态化设计变得很有价值。】

三、分析并解决问题，方案的价值在哪里

《解决问题的非常规思考法》作者迈克尔·卡莱特强调，面对问题“还有没有更好的解决办法？”当我们的大脑在经验的驱使下习惯于固定的思维时，意味着我们已陷于平庸。面对一时无法解决的问题，我们需要摆脱自动化思维，充分利用创造性、假设性、非真实性等批判性思维重新发现问题、分析原因、汇总结论，得出蕴含更多可能的解决方案。“求瓶子的容积”方法上的特殊性正好有利于产生方案的需要。

（一）方案设计，挑战性任务体现策略特征

课件出示活动要求：设计一个“求瓶子的容积”的解决方案：

【思考：方案的设计是理清思路、培养学生思维的一个很好的载体。设计方案的意图在于方法的特殊有利于方案的需要，需要以步骤的形式把思考推理的过程记录下来，并且这样的记录适合后续的交流活动，可以在了解学生原生态的思维上加以分析和引导，可以将策略意图逐步明显揭示。】

（二）方案交流，探讨策略的可行性

组织反馈，重点交流两个问题：

1.你是怎样求得瓶子的容积的？

2.水的体积加上空气的体积就是瓶子的容积了吗？为什么？

依次呈现上述方法，并请学生加以解释，在讨论中分析、补充，认识方案的合理性与可行性。

（三）方案整理，突出策略的作用

师：在同学们的讨论中，老师知道了：要求瓶子的容积，先求出水的体积，再加上空气的体积，因为空气的体积不规则，想到了把瓶子倒过来，转化成规则的圆柱体，在转化后空气的形状变了，但体积没有变。

（四）落实方案，比较策略的适用性

1.给出数据，计算并反馈。

师：现在如果要精确地求出这个瓶子的容积，你认为至少需要测量哪些数据？

生：需要测量圆柱的底面直径，水的高度和倒过来后空气的高度。

小结：同学们真厉害，想到了把瓶子倒过来这个巧妙的办法，求得了瓶子的容积。

2.展示不同，计算并反馈。

师：刚才还有一个小组的方案不一样，你们能看懂吗？

生：水很少的时候，水的体积×2+中间的圆柱的体积=瓶子的容积。

生：水比较多的时候，水的体积×2－重叠的圆柱的体积=瓶子的容积。

（请一位学生上来边演示边说）

师：大家能想象吗？用这个方法也能算出瓶子的容积，但没有直接用水的体积加空气体积简便。

【思考：方案的梳理是学生思维的梳理，在这个过程中学生通过讨论，从“不知”到“知了”，从“有困难”到“成功解决”，从“没道理”到“有道理”是学生经历解决问题的整个过程、积累活动经验的过程，同时学生在体验数学问题的探究性和挑战性中也获得了成功的喜悦。最后一种方案的呈现是对知识的提升与串联，意图让学生感受策略的适用性与转化的普遍性。】

四、过程回顾与反思，作何串联与提升

本环节，在问题解决的教学中强调策略的意义，是为了促成学生学会“数学地思考”。其一，在解决问题的过程中因成功解题的需要而形成选择相关策略的意识，体验具体策略的优越性。这可以归结为我们教学中的“举一”。其二，将形成的策略映射到解决问题的过程中去，运用具体的策略解决问题，完成对具体策略的重新建构。这一过程可归结为我们教学中的“反三”。

（一）经历问题解决的过程，培养策略意识

1.课件出示题目：一瓶装满的矿泉水，小明喝了一些后，剩下水的高度是10厘米。他把瓶盖拧紧后倒置放平，无水部分的高也正好是10厘米。瓶子内直径是6厘米。

师：根据这些信息，你能解决哪些问题呢？请你自己提出问题，并列式计算出答案。

师：你们用 π（6÷2）2×10=90π（立方厘米）这个算式解决了什么问题？

生：我用这个算式知道了水的体积。

生：我用这个算式知道了空气的体积。

生：我还知道了倒过来之后水的体积是不变的，所以倒过来水的体积也是90π立方厘米。

【思考：在经历了之前探究过程后，让学生自主地在练习过程中去发现问题、提出问题并解决问题，是让学生从头到尾地进行思考，并在“巧合”中进一步巩固“变与不变”，让学生对于策略的特征、策略的实用性进一步理解，同时也培养学生学会区别不同的问题采用不同的策略。】

（二）展开大背景，纳入转化思想体系

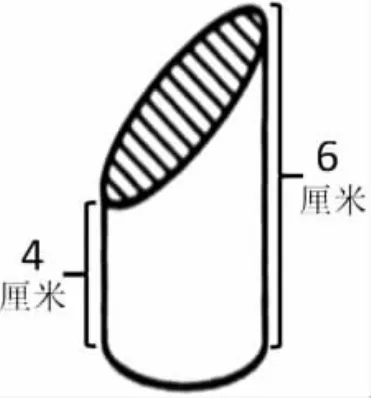
如上图，一个底面面积为20平方厘米的圆柱体，如果从中间斜着截去一段后，它的体积会是多少呢？

师：请大家想办法解决这个问题，写在纸上。

组织反馈：

生：找一个一模一样的木头，拼在上面，拼成一个底面积为20平方厘米、高为10厘米的圆柱再除以2，就是木头的体积。

生：我可以把4厘米上面的这段不规则的切掉，再把切掉的部分从中间横切成两半，把其中的一半拼上去，变成一个高为5厘米的圆柱。

全课小结：把不规则的转化成了规则的，像这样的方法我们在以前的学习中就用到过，你能举个例子吗？

生：求平行四边形的面积时，我们把平行四边形转化成了长方形。

生：求圆的面积的时候，我们把圆转换成了一个长方形。

师：求梨的体积，将它沉入水中，转化为水上升的体积；求三角形的面积，将它先转化成学过的平行四边形的面积，再除以2；还有我们今天的求瓶子的容积。

（课件依次呈现）

师：在以后的生活和学习中，我们还会遇到很多这样的问题，希望同学们能像今天一样，学会运用数学的思考方法找到解决问题的办法。

【思考：回顾这节课学生经历解决问题的过程，从“发现问题→方案设计→方案梳理→回顾反思”这四个环节，它与波利亚在《怎样解题》中提出的四个步骤“弄清问题——拟订计划——实现计划——回顾反思”不谋而合，关键要在弄清问题和拟订计划这两个环节中，引导学生找到解决问题的突破口，抽象出解决数学问题的基本模型；这四个环节更是与课标倡导的“四能”同步紧密，因此“且问且行”，即以问题驱动学习，随着问题的展开与深入，不断有新问题产生，不断去解决，这是解决问题教学的最佳状态。本课的亮点：其一是问题，其二便是策略。从发现问题、提出问题开始，随之而来采取什么方式处理与分析数量信息间关系、建立何种有效的数学模型解决，以及解决问题方法的普遍意义等是靠策略性知识来完成的，这便形成了对“策略”的需求。可见，策略是对方法本质的认识，是介于解决问题的方法与数学思想之间的连接纽带。】