多功能农用机器人路径规划的多种优化算法
王 辉, 王景良, 朱龙彪, 邵小江
(1.南通大学机械工程学院,江苏南通 226019; 2.江苏海事职业技术学院,江苏南京 211170)
城镇化进程加快、人口数量激增、耕地面积日益减少、农作物价格偏低等诸多问题持续突出,会严重影响农民种植作物的积极性。在此背景下,发展现代农业技术,研发农业机器人系列产品,对提高农户劳动生产率、改善农业生产环境、提高农业作业质量及提高农业机械化程度等具有极其重要的现实意义[1]。为加快农业机器人研发进程,世界各国都投入了大量的人力和物力支持,国内外学者经过多年的攻关研究,设计出了多种类型用于解决农业生产实际问题的机器人,如采摘机器人、移栽嫁接机器人、耕作机器人、喷药施肥机器人及饲养机器人等[2]。为解决农作物病虫害监测、工作环境监测、实现物料搬运功能,设计了一种多功能农用机器人。该机器人是集传感器、人工智能、计算机、图像处理、通信及控制工程等多学科前沿技术于一体的智能装置,具有柔性好、灵活性强、安全可靠、智能化程度高及通用性、适应性、可扩展性强等优点[3],可实现农作物病虫害监测,工作环境监测、物料或肥料搬运以及在特殊情况下的人员搜索救援等功能。为实现上述功能,解决路径规划问题是首要前提。针对路径规划问题,目前常用的有效方法主要有Dijkstra算法、遗传算法、蚁群算法、模拟退火算法、禁忌搜索算法等。为了解决多功能农用机器人路径规划问题,通过引入禁忌搜索算法、遗传算法、蚁群算法和模拟退火算法,对农用机器人路径规划过程进行研究。
1 数学模型建立
多功能农用机器人路径规划问题的实质是路径搜索问题,其目的是在已知有障碍物存在的工作环境中,系统根据机器人的当前位置、目标点位置及运行环境等相关信息,按照一定评价指标(如距离最短、程序耗时最少及收敛代数最小等)采用特定搜索策略,在环境地图中搜索出一条从起点到目标点的最优或次优无冲突路径,确保机器人能够沿着该优化路径顺利完成农作物病虫害监测、工作环境监测以及物料或肥料搬运等任务[4]。在路径规划中,系统要求农用机器人从原点出发,遍历各作物种植区1次,完成作物病虫害监测、工作环境监测或肥料搬运等,然后再返回至原点,这一过程可抽象为旅行商(TSP)问题。TSP问题作为经典组合优化NP难题,在问题规模复杂度较大的环境下,运用当前所提算法至今仍未得到精确解。由于各领域均有涉及TSP问题,因此,研究TSP求解方法对解决多领域复杂工程应用问题具有极其重要的现实意义和理论意义[5-6]。
多功能农用机器人的TSP问题可描述为:在已知各作物种植区和各作物种植区间距离的前提下,农用机器人从原点出发,遍历各作物种植区1次,完成系统指定任务,然后再返回至起始点,在此过程中寻找一条闭合回路,并确保该闭合回路长度最短[7]。其数学模型可描述为:绘制工作环境交通路网图,建立工作环境赋权图G=(V,E),其中,V表示作物种植区节点集,V={1,2,3,…,n};E表示各作物种植区节点间形成的可行路段集,E={e1,e2,e3,…,en};D表示各作物种植区节点间的距离集,即权重集,D={d(1,1),d(1,2),d(1,3),…,d(i,j),…,d(n,n)},其中,d(i,j)表示2个作物种植区节点间距离,i、j∈V。其数学模型方程式可表示为[8]:
(1)
(2)
式中:Lpath表示农用机器人在遍历各作物种植区中所能搜索到的最短路径长度;(xi,yi)、(xj,yj)分别表示i、j这2种作物种植区节点的坐标值。
2 算法设计
2.1 禁忌搜索算法
禁忌搜索算法(tabu search algorithm,TSA)是由Glover教授通过模拟人类智力过程而提出的一种亚启发式智能全局逐步寻优算法,因其具有记忆功能灵活、能跳出局部最优以及全局搜索能力强等优点,所以在优化组合、车间调度、路径规划、电路设计等领域得到了广泛应用[9]。基本思想是搜索可行解空间,按照领域选优原则,在当前解领域内寻找一个更优解。为避免算法陷入局部最优和出现死循环,需将该解添加到禁忌表中。随着迭代搜索进行,算法通过灵活使用禁忌表记录搜索过程,并按照特赦准则不断对记录数据进行更新,最终确保算法在搜索到局部最优解的同时又能越过局部最优解而实现全局最优解搜索[10-11]。算法流程可进行如下描述,步骤一:初始化算法各参数,给出初始解,禁忌表置空TB=φ;步骤二:判断算法搜索过程是否满足终止准则,如果满足,则算法搜索过程结束,输出搜索结果,否则转至步骤三;步骤三:由当前解产生邻域解,并从中确定候选解;步骤四:判断候选解是否满足特赦准则,如果满足,则将最佳状态的候选解作为当前解。另外,还要按照先进先出的原则,用新当前解对应的禁忌对象替代最早进入禁忌表的禁忌对象,然后算法转至步骤二,否则转至步骤五;步骤五:判断各候选解对应对象的禁忌属性,从候选解集中选取非禁忌对象对应的最佳状态为新的当前解,再按照先进先出原则更新禁忌表,然后转至步骤二。
2.2 模拟退火算法
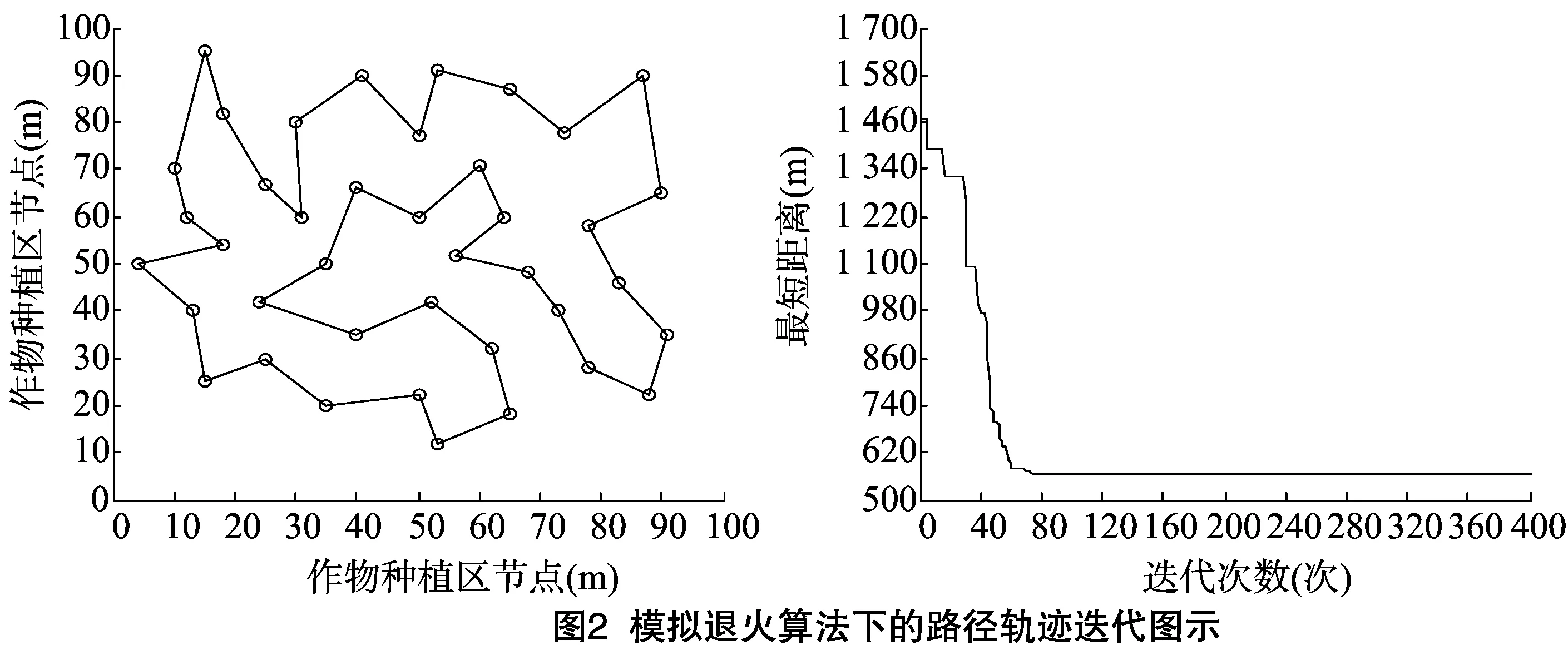
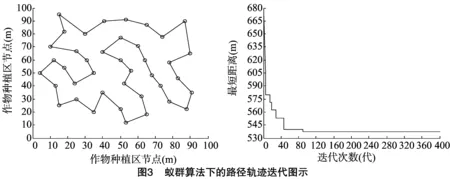
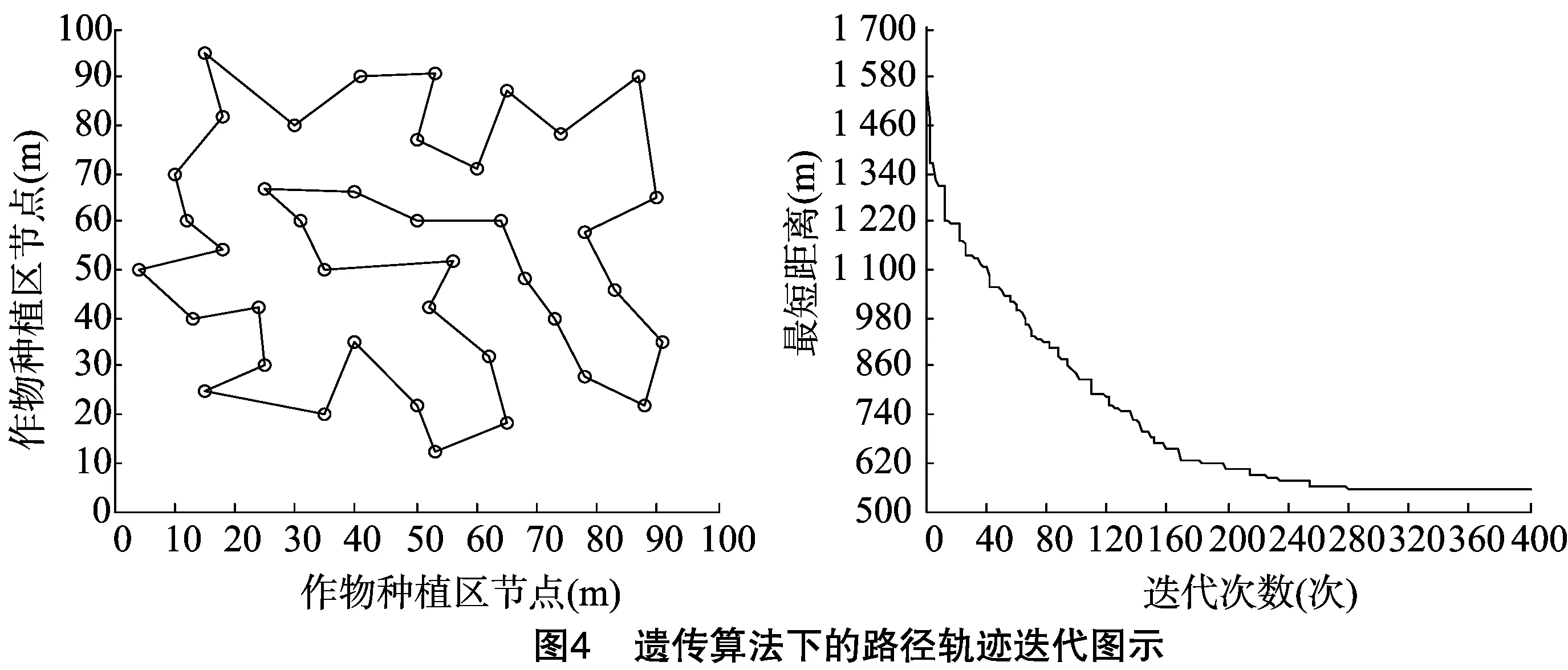
模拟退火算法(simulated annealing algorithm,SAA)是Metropolis等受固体物质退火原理启发而提出的一种通用的自适应启发式随机优化搜索算法[12],具有鲁棒性强、全局收敛速度快、隐含并行性以及较强的环境适应能力等优点。基本思想是从初始时刻某一预设温度出发,随着迭代搜索进行,伴随温度参数不断下降,按照Metropolis准则,结合概率突跳特性,在可行解空间中随机寻找目标函数的全局最优解,即按照Metropolis准则以一定概率跳出局部最优陷阱而最终趋于全局最优解。选用模拟退火算法解决TSP的具体步骤如下[13],步骤一:初始化算法参数,设定初始温度、终止温度、降温速率以及链长等参数;步骤二:采用随机排列方法生成初始解;步骤三:采用二邻域变换法对当前解进行变换并生成新解,即产生新的路径数组;步骤四:判断Metropolis准则是否接受新解,判断依据如方程(3)、(4)所示,如果Δδ<0,则以概率1接受新解,反之则以概率exp(-Δδ/T)接受新解;步骤五:判断算法是否满足终止条件T Metropolis准则方程式如下[14]: Δδ=f(S2)-f(S1); (3) (4) 式中:S1、S2分别表示当前解和新解;f(S1)、f(S2)分别表示当前解路径和新解路径;Δδ表示当前解和新解路径差。 蚁群算法(ant colony optimization,ACO)是由Dorigo等通过模拟蚂蚁觅食行为而提出的一种新型优化仿生进化算法。该算法是基于正反馈机制,利用蚂蚁遗留在爬行路线上的信息素轨迹强弱和状态转移概率实现最优解搜寻。因其具有分布计算、信息正反馈、启发式搜索以及较强的鲁棒性等优点,所以被广泛用于解决路径规划、生产调度、网络路由以及图像处理等问题[15]。选用蚁群算法解决农用机器人TSP问题具体步骤如下,步骤一:初始化算法参数,包括搜索次数、蚂蚁数量、初始信息素浓度以及其他各主要调节参数等;步骤二:算法开始迭代搜索,将所有蚂蚁初始条件下所在的各作物种植区节点加载到当前解集中,在算法执行过程中,蚂蚁对下一作物种植区节点的访问可按照方程式(5)确定;步骤三:判断所有蚂蚁是否完成对作物种植区节点访问,若是,则计算所有蚂蚁搜索的路径长度,并记录最优解,然后按照方程式(6)、式(7)和式(8)对各作物种植区连接路径上的信息素进行更新;步骤四:判断是否满足终止条件N≤Nmax,如果满足,则转至步骤二,否则,算法搜索结束,输出结果。 节点转移概率函数式如下[16]: (5) 式中:pijk表示转移概率;allowedk表示下一步允许选择的作物种植区节点集合;τij表示路段(i,j)的信息素轨迹强度;ηij表示启发函数因子;α表示信息素轨迹相对重要程度因子;β表示期望程度因子。 信息更新规则方程式如下: τij(t+1)=(1-ρ)·τij(t)+Δτij; (6) (7) (8) 式中:ρ表示信息素挥发系数;Δτij表示路段(i,j)上的信息素增量;Q表示信息素增强因子。 遗传算法(genetic algorithm,GA)是由Holland与其同事在自然选择和遗传理论的基础上,通过将自然界生物进化过程中的适者生存法则与种群内部染色体信息随机交换机制进行有效结合,而发展起来的一种具有高效全局搜索能力的启发式智能随机优化算法。该算法主要由编码、种群规模设定、适应度评估函数、选择、交叉以及变异操作组成,具有并行计算、鲁棒性强、全局寻优能力强以及易与其他启发式算法结合等特点[17-18]。选用遗传算法解决农用机器人TSP问题的具体步骤可表述为:(1)采用整数编码方法将TSP问题空间解数据编码成遗传算法可以识别的串结构数据;(2)编码操作结束后,随机产生1个包含M个个体的种群,并确定算法初始搜索点;(3)根据目标函数设定种群适应度函数,具体如方程式(9)所示,依次计算种群中M个个体的适应度值,并以各个体适应度值的大小判断种群中个体的优劣;(4)以适应度方程式(9)作为评价标准,采用轮盘赌法以一定概率从种群中筛选出优良个体,确保优良个体的某些重要基因遗传到下一代;(5)采用部分映射交叉方法作用于步骤(4)中的种群;(6)确定变异对象,随机选取2点,以一定变异概率置换其位置;(7)对步骤(6)中种群进行进化逆转操作,产生新种群;(8)判断终止条件N>Nmax是否满足,若满足,则搜索过程结束,输出结果,反之则算法转至步骤(3)。 适应度函数方程式如下: (9) 为测试所提方法在多功能农用机器人路径规划中的实际效果,分别选用含有25、30、40、50个作物种植区的环境模型作为研究对象,以距离最短、程序耗时最少、收敛代数最小为评价指标,在Matlab软件平台上对所提方法进行仿真测试。为了使测试数据更好反映算法实际性能,每组数据均作了多次重复测试,结果见表1。另外,在作物种植区节点规模为50的环境模型中,由于禁忌搜索算法、模拟退火算法、蚁群算法无法搜索到满足目标函数的优化路径,因此,表1未给出该环境模型下的测试数据。 表1 各算法的测试数据 由表1数据可知,在作物种植区节点规模为25的环境模型下,TSA和ACO搜索路径的最优解长度相同且最短,ACO搜索路径的标准差和开始收敛代数均为最小,TSA的程序耗时最少;在节点规模为30的环境模型下,ACO搜索路径的长度和标准差均为最小,SAA最先开始收敛,GA和ACO的数据测试次数相同且最少,TSA的程序耗时最少;在节点规模为40的环境模型下,ACO搜索路径的长度和标准差均为最小,SAA最先开始收敛,GA的数据测试次数最少,TSA的程序耗时最少。综上分析并结合表1数据可知,在节点规模较小环境模型下,算法全局搜索能力排序为ACO>GA>TSA>SAA;最优解稳定性排序大体为ACO>GA>SAA>TSA;收敛性能排序大体为SAA>ACO>GA>TSA,程序执行效率排序为TSA>SAA>GA>ACO;最优解获得难易程度排序为GA>ACO>TSA>SAA;在节点规模较大环境模型下,GA的全局搜索能力优于其他3种算法。 各算法在节点规模为40的环境模型下的测试结果如图1、图2、图3和图4所示。 图5为遗传算法在节点规模为50的环境模型下的路径轨迹迭代图。由仿真测试结果可知,在节点数为40的环境模型下,各算法均能为农用机器人规划出一条距离最短的优化路径,但在节点数为50的环境模型下,仅有GA能为其规划出距离最短的优化路径。由图1至图4还可看出,SAA收敛性能优于ACO,ACO优于GA,GA优于TSA。此外,对比不同环境模型下的测试数据可知,针对节点规模较大的环境模型,GA可通过增大种群数量和增加收敛代数获取最优路径。 本研究提出采用禁忌搜索算法、模拟退火算法、遗传算法和蚁群算法解决多功能农用机器人路径规划问题。为验证算法的有效性,分别以作物种植区节点数为25、30、40、50的环境模型为实例,对多功能农用机器人路径规划过程进行仿真测试。由测试结果可知,在满足目标函数约束的条件下,各算法均能为农用机器人规划出评价指标最好的优化路径;在作物种植区节点规模较小环境下,虽然蚁群算法具有最强的全局搜索能力和较好的收敛性能,但程序执行效率最低;遗传算法虽能通过增大种群数量和增加收敛代数解决农用机器人节点规模较大路径规划问题,但收敛性能较差;虽然禁忌搜索算法和模拟退火算法的全局寻优能力较差,但其程序执行效率高,因此,可考虑通过算法融合策略来增强其全局寻优能力。 参考文献: [1]姬江涛,郑治华,杜蒙蒙,等. 农业机器人的发展现状及趋势[J]. 农机化研究,2014(2):1-4,9. [2]林欢,许林云. 中国农业机器人发展及应用现状[J]. 浙江农业学报,2015,27(5):865-871. [3]王宝梁,薛金林. 开放式系统农业机器人技术概述[J]. 农机化研究,2013(6):8-12. [4]Zhang X,Zhao Y,Deng N,et al.Dynamic path planning algorithm for a mobile robot based on visible space and an improved genetic algorithm[J]. International Journal of Advanced Robotic System,2016(13):1-17. [5]张鑫龙,陈秀万,肖汉,等. 一种求解旅行商问题的新型帝国竞争算法[J]. 控制与决策,2016,31(4):586-592. [6]Dewil R,Vansteenwegen P,Cattrysse D.A review of cutting path algorithms for laser cutters[J]. International Journal of Advanced Manufacturing Technology,2016,87(5/6/7/8):1865-1884. [7]Michail O,Spirakis P G.Traveling salesman problems in temporal graphs[J]. Theoretical Computer Science,2016(634):1-23. [8]王辉,朱龙彪,朱天成,等. 基于粒子群遗传算法的泊车系统路径规划研究[J]. 工程设计学报,2016,23(2):195-200. [9]李阳,李文芳,马骊,等. 混合退火算法求解旅行商问题[J]. 计算机应用,2014,34(增刊1):110-113. [10]汪定伟,王俊伟,王洪峰,等. 智能优化方法[M]. 北京:高等教育出版社,2007. [11]邵陆寿. 优化设计方法[M]. 北京:中国农业出版社,2007. [12]巩敦卫,曾现峰,张勇. 基于改进模拟退火算法的机器人全局路径规划[J]. 系统仿真学报,2013,25(3):480-483,488. [13]潘国强,胡俊逸,洪敏,等. 考虑GIS的物流配送区域划分与路径规划算法[J]. 大连海事大学学报,2015,41(1):83-90. [14]郁磊,史峰,王辉,等. MATLAB智能算法30个案例分析[M]. 2版.北京:北京航空航天大学出版社,2015. [15]Wang J G,Wang N,Jiang H Y.Robot global path planning based on improved ant colony algorithm[C]. Paris:International Conference on Material,2015:2099-2102. [16]Cao J.Robot global path planning based on an improved ant colony algorithm[J]. Journal of Computer and Communications,2016,4(2):11-19. [17]Jiang M,Fan X,Pei Z,et al.Robot path planning method based on improved genetic algorithm[J]. Sensors and Transducers,2014,166(3):255-260. [18]雷英杰,张善文. MATLAB遗传算法工具箱及应用[M]. 西安:西安电子科技大学出版社,2014.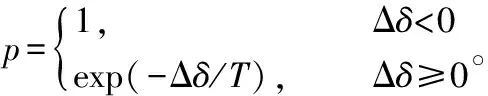
2.3 蚁群算法
2.4 遗传算法
3 仿真试验与分析


4 结论