基于傅里叶级数拟合的女装图案流行趋势预测

荣 蓉，赵丽妍，韩曙光

（浙江理工大学，a.服装学院；b.国际教育学院；c.理学院，杭州310018）

凭借着巨大的人口红利，中国已然成为全球最大的服装购买和制造国。随着经济全球化的日趋加深，中国正积极从服装大国向着服装强国发展，而成为服装强国就需要中国服装产业具备一定引领时尚走向的能力。能够抓住当下的流行趋势，甚至创造流行趋势，将是未来中国服装产业的重要任务。然而，我国的女装品牌总体上在流行趋势方面的预测能力非常薄弱，女装的设计主要是跟随国际一线大牌进行模仿设计，或者依靠设计师的个人设计经验，专业的服装设计企划团队得不到重视，同时由于女装流行趋势方面的数据缺乏，没有数据的支撑使得我国女装行业在流行趋势方面的敏锐度不足。而在我国女装设计要素流行趋势的研究中［1］，对图案流行趋势预测的研究较为少见，并且均是从设计经验的角度对图案流行趋势做出了定性指导，并未有更加准确可靠的定量分析［2－4］。因此，准确、可靠、实用的女装图案流行趋势预测方法是迫切需要的。

一、流行与服装流行预测概述

（一）流行的定义及相关概念

在心理学中，流行是一种在社会活动中展现出来的心理现象，代表着某种文化或某些文化的集合。流行是指在特定群体和地区中以一定的时间规律广为传播的文化［5］。流行的含义包括三个方面［5］：a）对某种生活模式或标本的追从造就了流行的产生，流行涉及的范围广泛并且有着多样的体现形式；b）对某种生活模式或标本的追从者达到一定数量才能构成流行；c）流行有着显著的时变属性，有些流行会演变成传统。流行的内容根据领域的差别有所差异，但都展现出共同的特征：新奇性、现实性、短时性、周期性。影响流行形成的因素大致可以分为：a）社会因素。流行会受到社会文化的约束，依靠大众传播工具的宣传，并且需要一定的经济基础。b）心理因素。个体或群体的从众与模仿，个体或群体的求新欲望，个体或群体的自我防御和自我显示都会影响流行的形成，并且追随流行也会存在个体差异。

（二）服装流行预测概述

服装流行预测是对以往和当前服装及其周边事物的流行状态进行分析，并依此用特定方法对未来某个时期的服装及其周边事物的流行状态进行预测［6］。

1.服装流行预测的内容

服装流行预测的研究对象通常包括五个方面［7］：a）服装轮廓。作为最能够反映流行的特征，轮廓线的改变直观地表现出流行状态的变化。b）结构造型。结构的处理方式体现了流行趋势的特征，合体程度的掌握、分割线条的形状处理、开身变化、袖肩造型等都会随流行趋势的变化而变化。c）材料。由于材料承载了服装的设计，材料的流行先行于服装的流行，面料的色彩、肌理、纹路等都有着明显的流行变化趋势。d）色彩。服装设计师着重于应用色彩的搭配去表达所需的意境，色彩在时装中占据着主导地位，不同时期的色彩应用有着不同的倾向性。e）细节与工艺。在不同的流行季节中，服装的细节都不尽相同，加工过程也会采取不同的工艺。以上所有要素综合在一起所体现出来的风格指示了流行的方向，设计师在进行服装设计时必须有所把握［5］。

2.服装流行预测的发布规律和渠道

在服装产业内，通常由专业的预测部门或团体、领先的服装设计生产企业和流行领域的专家等完成服装的流行预测。基本上是按照流行要素－纤维－面料－成衣－销售的流程进行服装流行预测的发布。其中，专业的预测部门或团体主要发布服装设计要素的流行预测，领先的服装设计生产企业同专业的预测部门或团体合作发布纤维与面料的流行预测，而服装设计、生产机构独立发布服装的生产和销售趋势预测。在国际上，存在着很多著名的服装流行预测机构，国内也成立了不少服装流行预测机构。这些预测机构通常会选择在一些专业预测杂志、专业时尚杂志、专业会展、专业网站等发布其流行预测结果［8］。

3.服装流行预测的方法与步骤

在服装流行趋势预测方法中，按照预测方法性质分类可分为定性预测和定量预测［9］。定性预测是服装流行趋势研究者根据历史和当前服装流行趋势的变化，凭借自身的从业经验和常识，对未来服装流行趋势的发展进行预判，其中包括直觉预测法和流行专家会议预测法［10］；定量预测是服装流行趋势研究者通过对历史和当前服装设计要素的数据进行分析，借助合适有效的数理统计手段和数学模型推算出未来服装流行的发展变化，其中包括流行要素情报预测法、流行要素市场统计分析预测、流行要素偏爱度预测法、流行要素回归分析预测法等方法［11］。一般来说，服装流行预测的过程，从开始的调研到最后的发布分为如下几个步骤，如图1所示［12］。

图1 服装流行预测步骤

二、女装图案流行趋势预测模型构建与检验

1.流行趋势预测模型的选取

在服装流行趋势预测研究中，流行趋势会受很多因素影响，且结合实际的销售百分比数据可知，其趋势具有明显的周期性、非线性等特征。在对流行趋势进行数学建模时，选取合适的拟合方法十分重要，不仅要尽可能准确地反映不同时间点的数据值，还要准确地表征出数据的趋势变化规律。

根据服装流行趋势具有周期变化波动的特点，针对此类周期非线性系统，传统的线性预测方法，如线性回归、时间序列等方法，虽然简单但难以解决非线性预测问题［13－19］。在非线性拟合方法中，常见的方法有指数法、傅里叶级数法、高斯法、插值法、多项式法、幂级数法等。其中，在服装领域，多项式拟合法较为常用。但是，当预测时间点远离于样本数据时间点时，所得数学模型预测结果会由于高次项的存在而发散，无法有效对于中长期时间点的数据进行预测。在选取适用于服装设计要素流行趋势预测模型时，不仅要考虑预测值的准确性和精度，还要考虑所选取的模型能否有效地呈现出流行的周期性趋势。

在自然界和实际工程中经常会接触到周期性运动的变量，反映到数学上，就是通常所说的函数的周期性。任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示，傅里叶级数拟合便是研究用一些正弦项和余弦项之和式去逼近一个函数的问题［13］。故本文中选取傅里叶级数拟合法作为女装图案的流行趋势预测模型。

散点销售百分比数据可构成平滑曲线且具有明显的周期性，故可用周期函数表示，即

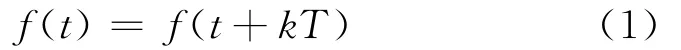
式中：T为周期函数f（t）的周期，k＝0，1，2，…。

在实际工程中所遇到的大多数非正弦周期函数都是满足Dirichlet条件的［14］，则函数f（t）可以表示为

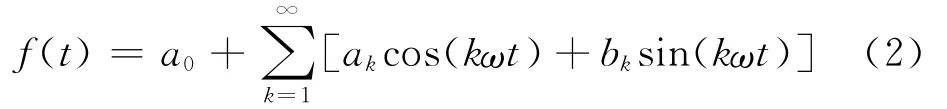
式中：a0、ak、bk为傅里叶系数，式（2）是由若干个正弦项和余弦项叠加而成。但对离散的每月销售百分比数据来说，其月销售数据的个数并非无限的，因此只能进行有限项的傅里叶级数拟合。设n个月销售百分比数据所组成的序列为Y（t），即

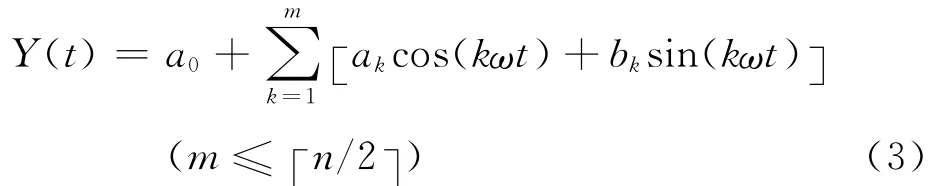
写成矩阵的形式为AX＝Y，其中：

因为m≤［n／2］，可用最小二乘法求解X，其最小二乘法解为

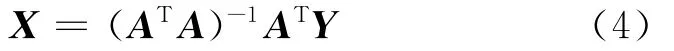
由式（4）即可求出傅里叶级数拟合中各项的傅里叶系数［15］。

拟合方程的项数直接影响着拟合的效果，为达到最好的拟合效果，在模型建立之后需要选取合适的拟合方程项数。首先将所有销售百分比数据代入项数为m的傅里叶级数拟合方程中进行拟合，并根据误差平方和、离差平方和、调整后的离差平方和以及标准差等统计量检验拟合效果。若拟合效果不满足需求，则将所有销售百分比数据再次代入项数为m－1的傅里叶级数拟合方程中进行拟合，重复上述步骤，直至找到拟合效果好的拟合方程［16］。

2.某品牌女装各图案销售数据的分析与归纳

本文中的女装图案流行趋势预测研究选取了市面上常见的11种图案大类作为分析对象，包含条纹、格子、圆点、卡通、花色、字母、纯色、动物纹、人物、抽象图案以及碎花／植物花卉，其研究的是某一大类图案的流行度变化，每一种图案大类代表的是某件女装具备该类型的图案特征或相似的图案特征。女装图案流行趋势预测模型是在某电商女装品牌2011年4月至2017年3月各图案种类服装销售数据的基础上建立起来的，所有数据均为该电商女装品牌的后台数据并经许可获得，选择该电商女装品牌作为研究对象是由于其数据可方便获得而且其在女装市场上有一定的影响力。但是，这些销售数据均为绝对销售量，单纯从数值上去分析流行程度容易造成绝对销售数据量大不一定流行的现象，所以需要对这些绝对销售量进行进一步处理，用销售百分比更能有效反映出女装图案的流行趋势，如表1－表8所示，其中空缺数据代表该月份未发生此类图案女装的消费。对某电商女装品牌2011年4月至2017年3月各图案种类服装的销售百分比数据进行分析，对每月销售量百分比最高和最低的图案种类进行标注，如表1－表8所示，其中深灰色代表每月销售百分比最高的图案种类，反之，浅灰色代表最低的图案种类。

表1 某电商女装品牌2011年4月至2011年12月各图案种类服装的销售百分比数据　%

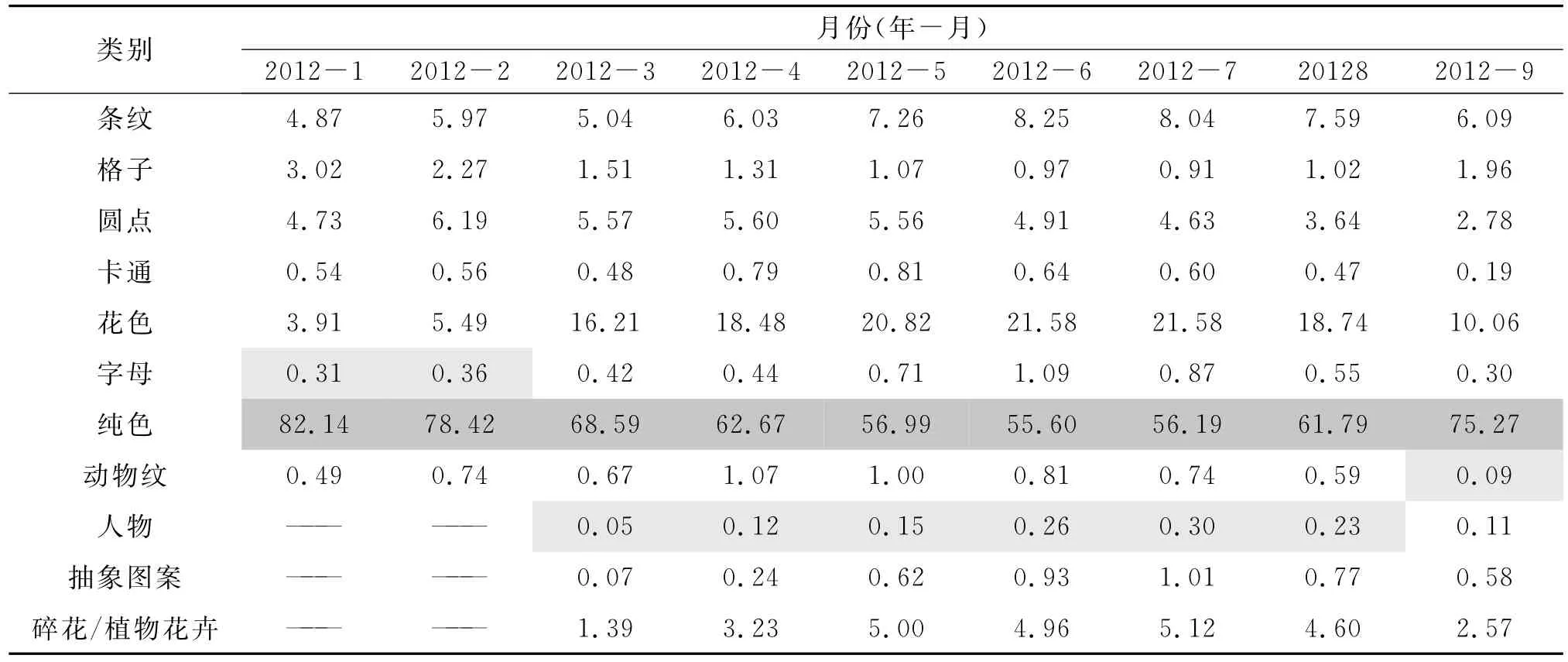
表2 某电商女装品牌2012年1月至2012年9月各图案种类服装的销售百分比数据　%

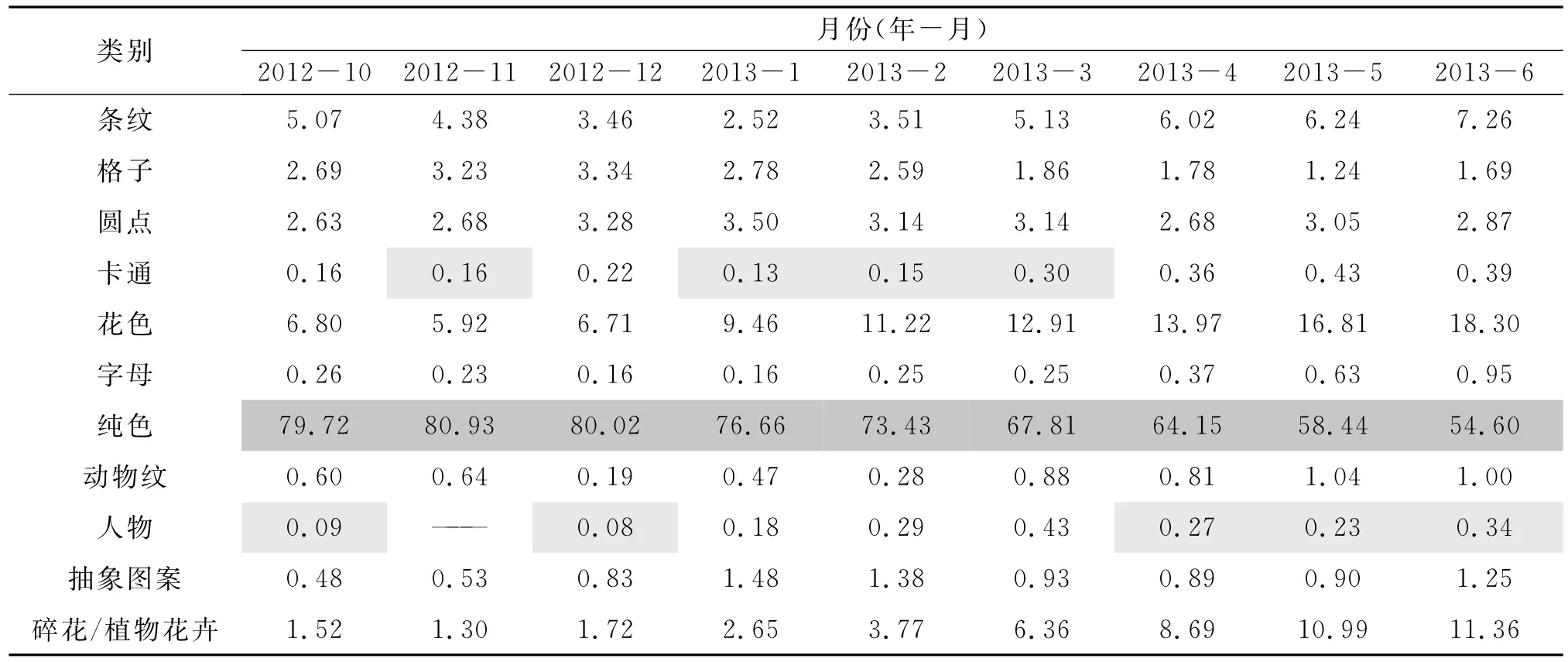
表3 某电商女装品牌2012年10月至2013年6月各图案种类服装的销售百分比数据　%

表4 某电商女装品牌2013年7月至2014年3月各图案种类服装的销售百分比数据　%

表5 某电商女装品牌2014年4月至2014年12月各图案种类服装的销售百分比数据　%

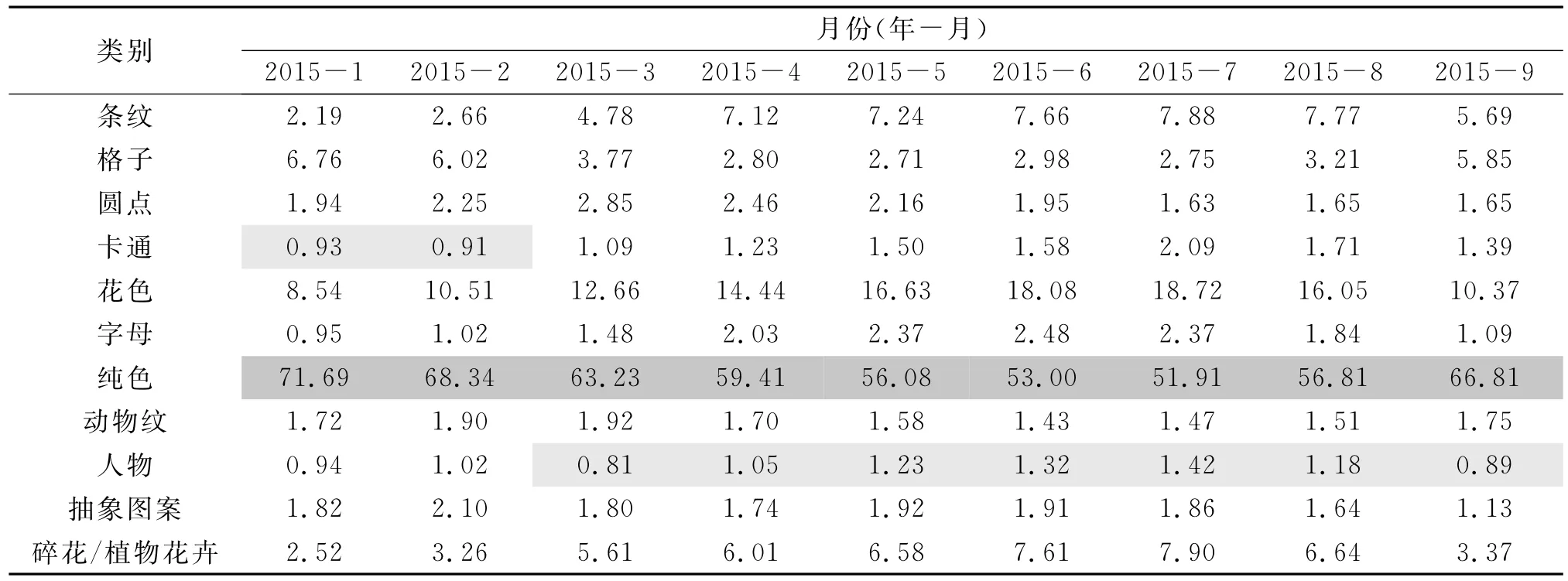
表6 某电商女装品牌2015年1月至2015年9月各图案种类服装的销售百分比数据　%

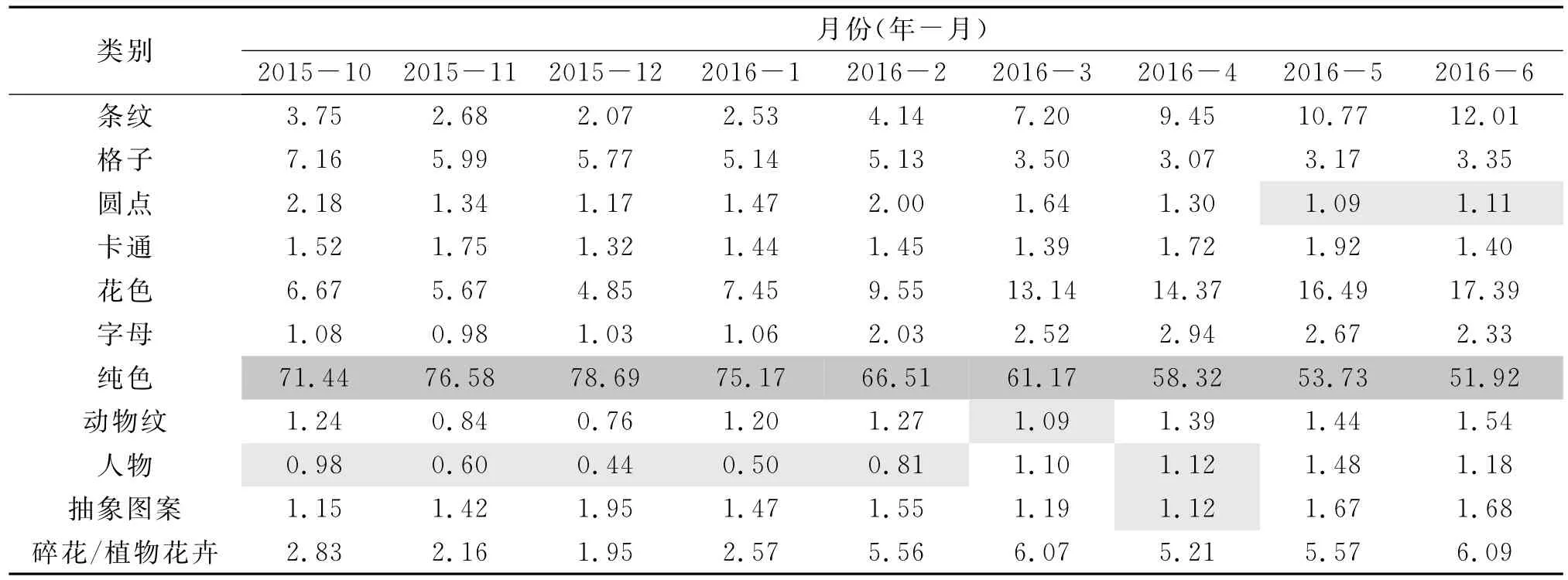
表7 某电商女装品牌2015年10月至2016年6月各图案种类服装的销售百分比数据　%

表8 某电商女装品牌2016年7月至2017年3月各图案种类服装的销售百分比数据　%

表8续

从表1－表8中可以初步获知，每个月中纯色图案的女装销售百分比最高，动物纹、卡通、字母、人物、动物纹、抽象图案以及圆点图案均有过月销售百分比最低的情况，其中人物图案的女装次数最多。从表1－表8中可以看出，纯色图案的女装占据了每月销售百分比的第一位，其百分比的区间为［41.38%，84.22%］，每个月几乎过半的销售量来自于纯色图案的女装。花色图案和条纹图案的女装保持着良好的流行度，两者分别为第二流行和第三流行的图案，且每个月的销售百分比数值较为接近。仅从销售百分比来看，人物图案的女装出现销售百分比最低的次数最多，其销售百分比远远小于其他种类的图案。由于无图案的纯色女装往往是女装中的经典款，月月占据着很大的销售份额。因此，本文规定排序除第一以外的图案可参与到流行趋势的预测研究中。虽然对纯色图案女装的流行程度没有流行趋势预测的研究意义，但是仍可对其销售量进行预测，为生产商、销售商提供产量、销量估计。

根据表1－表8所示数据，针对不同图案种类女装的销售百分比数据绘制散点折线图，各种类图案的散点折线图如图2所示。根据图2所示折线图，可将销售百分比变化规律大致划分为两种：第一种情况，变化周期清晰可辨的，其中包括条纹、格子、花色、纯色、碎花／植物花卉5种图案种类，该组折线图的变化规律具有很明显的以一年为周期的起伏形状；第二种情况，变化周期不易直接观察的，其中包括圆点、卡通、字母、动物纹、人物、抽象图案6种图案种类。

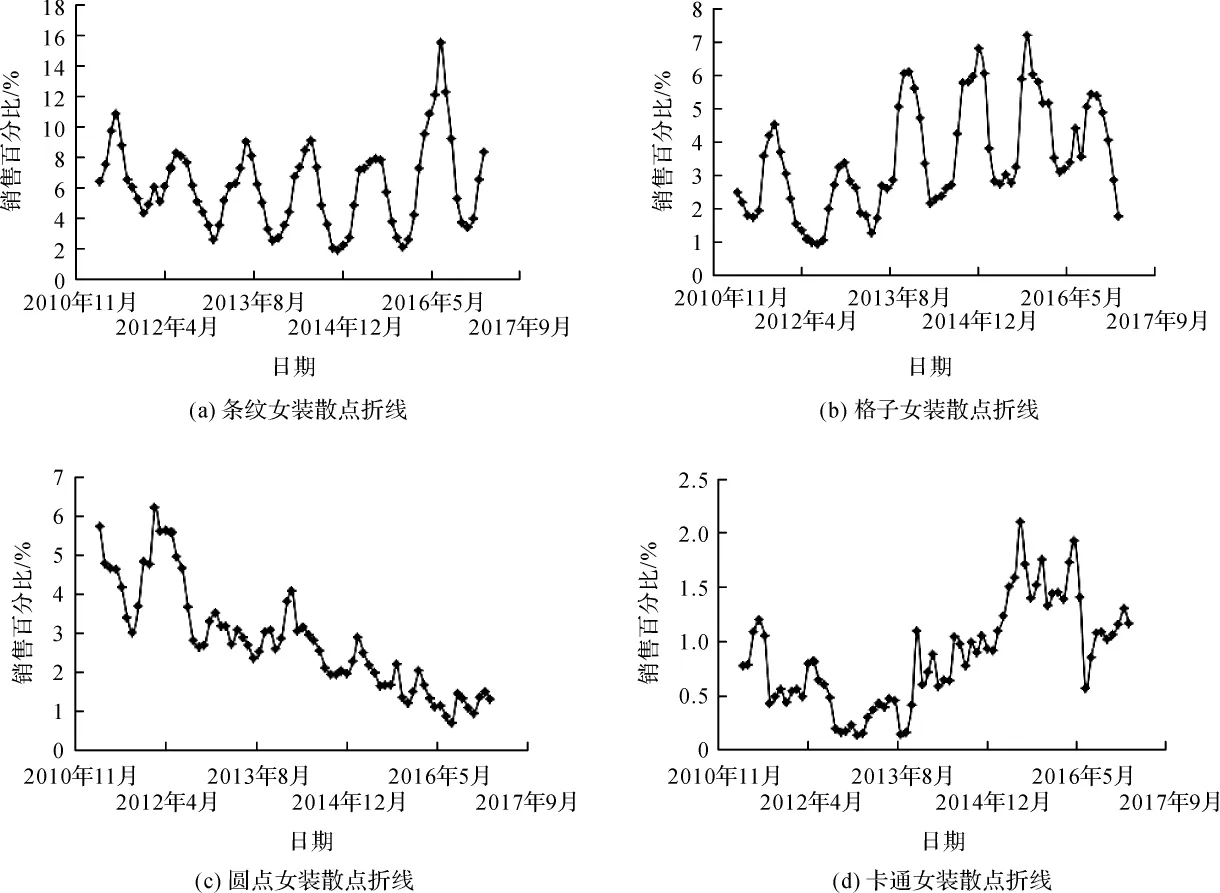
图2 根据不同图案种类女装的销售百分比数据所绘制的散点折线图

在第二种情况中，6种图案的女装销售百分比均在5%以下波动，可认为消费者对这些图案的消费需求往往是随机的、冲动的，在平常的供应中仅需维持少量库存即可，故不适合对其进行图案流行趋势预测。经过以上分析，选取条纹、格子、花色、纯色、碎花／植物花卉6种图案进行流行趋势预测，其销售百分比较大且具有鲜明的随时间变化趋势。不过从原始数据中可知，纯色的销售百分比虽然也有上升下降的变化规律，但其一直处于每月销售百分比的第一位，无流行程度的变化，故不对其流行的趋势进行研究与预测。

现对第一种情况中的图案流行状态进行分析，图案的流行程度变化遵循低流行－中流行－高流行－中流行－低流行的循环发展。在女装设计中，图案的变化是直接受季节的影响做规律性运动的，根据图2所示的第一种情况的图案折线图也可以发现其有着明显的季节性变化现象。对除了纯色图案以外的第一种情况的图案（条纹、格子、花色、碎花／植物花卉）的数据进行分析，可以发现每个夏季条纹、花色、碎花／植物花卉图案达到最高流行度，格子图案达到最低流行度，而每个冬季则反之。上述的流行度变化过程在每一年都会反复出现，仅在幅度上有所不同。因此，可以发现女装图案流行变化曲线的周期由春夏季和秋冬季组成，时长为1年，其中条纹、花色、碎花／植物花卉等类型的图案，春夏季达到最流行秋冬季达到最不流行，格子等类型的图案，春夏季达到最不流行秋冬季达到最流行。总而言之，图案的流行变化规律是以秋冬季（或春夏季）的低流行度开始，经过半个周期后达到春夏季（或秋冬季）的高流行度，再经过半个周期以低流行度结束，如此循环。

3.流行趋势预测模型的构建

参考文献［17］中的实验数据处理方法，现选取条纹图案的女装所有销售百分比数据进行模型构建，自2011年4月至2017年3月的销售百分比数据如表9所示。

表9 自2011年4月至2017年3月条纹类图案的女装销售百分比数据　%

预留2017年3月的数据进行检验，将2011年4月至2017年2月的数据导入Matlab中，参考文献［18］中的时间序列分析方法，设时间为X轴，销售百分比为Y轴，2011年4月为时间原点0，2017年3月为7.1，一个月间隔为0.1，并调用Matlab的cftool函数拟合工具箱进行函数拟合。本文分别对2011年4月至2017年3月条纹图案女装的销售百分比数据进行了一阶至八阶傅里叶级数拟合，其结果如图3所示。从图3可知，考虑误差平方和、离差平方和、调整后的离差平方和以及标准差等统计量和傅里叶级数拟合方程的复杂度［19］，建议选取六阶傅里叶级数拟合方程作为女装图案流行趋势预测模型，其表达式为：

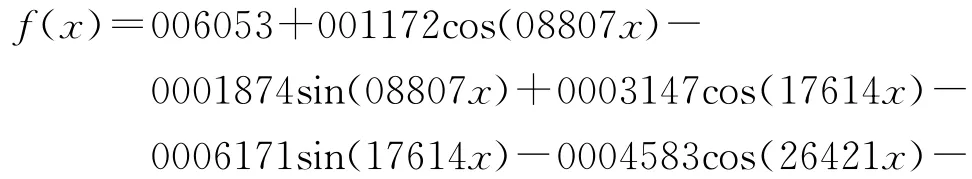
其误差平方和为0.0044、离差平方和为0.9153、调整后的离差平方和为0.8960、标准差为0.0088。总体而言，该六阶傅里叶级数拟合预测模型具有较高拟合度和还原度，可以对流行趋势变化做出很好的描述。

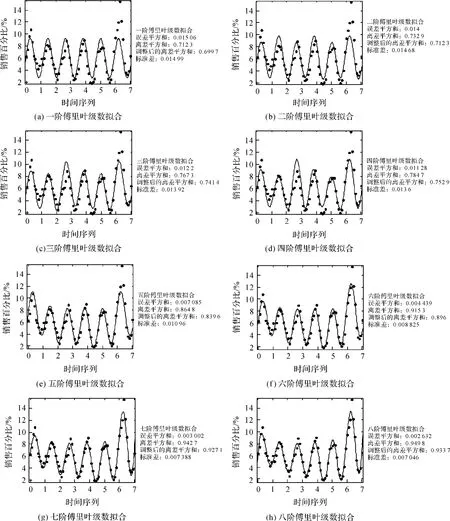
图3 一阶至八阶傅里叶级数拟合结果及相关指标参数

4.流行趋势预测模型的检验

将预留2017年3月的数据（x＝7.1，y＝8.26%）与f（7.1）＝5.71%比较，误差结果可接受，并且由于采用傅里叶级数拟合的方法，数学模型的趋势预测将会更加准确。从图2可知，条纹图案的女装销售百分比在2017年3月时呈现继续上升的趋势，故可将2017年4月（x＝7.2）带入f（x），可得f（7.2）＝7.32%，此结果即为对2017年4月条纹图案销售百分比的预测值，说明条纹图案的女装逐渐呈现出流行的趋势。由于采用傅里叶级数拟合，其对现有数据的还原度相比于多项式拟合有所降低，但其对流行趋势的走向把握要高于多项式拟合，不易出现随着预测时间点的延伸而导致函数发散的现象。

图4为基于六阶傅里叶级数拟合函数所得出的条纹图案流行趋势图，可以看出该预测模型对于周期性的流行变化有着很好的刻画。同样地，表1－表8中所提到的其余种类的图案也可以按照本文中的流行趋势预测模型建立方法，得出每种图案相应的流行预测模型，并且基于这些预测模型可以获得未来某一时刻各种图案的流行状态，将不同图案的流行状态预测数据汇总可以得到完整的图案流行趋势变化规律。

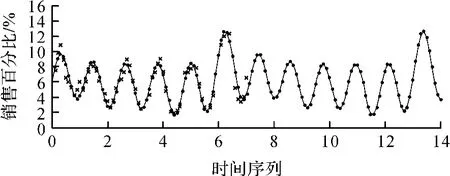
图4 基于六阶傅里叶级数拟合函数所得出的条纹图案流行趋势图

三、结 语

本文首先对流行及服装流行预测进行了阐述，收集了某电商女装品牌以图案进行分类的销售数据，对销售数据进行了分析归纳，选取了傅里叶级数拟合作为女装图案的流行预测模型，定量构建出了女装图案流行预测的数学表达式，对历史图案数据进行了检验，对未来图案流行趋势进行了预测。本文所提出的方法着重于对于流行趋势的表述，对不同图案的女装销售有一定的指导意义，对不同图案的女装流行趋势有着准确的预测。基于文中所提出的预测方法，日后随着销售数据样本的不断积累，其预测结果可以变得更加准确。同时，该预测方法可以用于其他不同类别的服装设计要素流行趋势预测中，使得对服装流行趋势的把握更加全面。

参考文献：

［1］穆慧玲.服装流行趋势［M］.上海：东华大学出版社，2016.

［2］林琴约.服装图案流行探索［J］.浙江纺织服装职业技术学院学报，2002，1（2）：21－25.

［3］孟萍萍.服装流行元素的解析与设计应用［D］.天津：天津工业大学，2008.

［4］程雅娟.几何图案对毛衫风格的影响研究［D］.无锡：江南大学，2006.

［5］Myers D G.Social Psychology［M］.New York：McGraw－Hill Education，2012.

［6］沈雷.服装流行预测教程［M］.上海：东华大学出版社，2013.

［7］邱影.浅谈服装设计要素［J］.黑龙江科技信息，2009（19）：65－65.

［8］杨威.服装设计教程［M］.北京：中国纺织出版社，2007.

［9］李熠，吴志明.服装流行色预测方法及量化思想比较分析［J］.纺织科技进展，2006（2）：82－83.

［10］宁宣熙，刘思峰.管理预测与决策方法［M］.北京：科学出版社，2003.

［11］顾雯.基于波浪理论与预测学方法的国际男装流行色趋势预测研究［D］.上海：东华大学，2012.

［12］刘晓刚.服装学概论［M］.上海：东华大学出版社，2011.

［13］Zygmund A.Trigonometric Series［M］.Cambridge：Cambridge university press，2002.

［14］文亮.分数傅里叶变换及其应用［D］.重庆：重庆大学，2008.

［15］张小飞，张效丽.基于傅里叶模型的服装出口分析及预测［J］.山东纺织经济，2012（1）：13－15.

［16］丛志鹏，梁军，李乃永.基于傅里叶级数的故障电压、电流的拟合方法［C］／／中国高等学校电力系统及其自动化专业学术年会.2007.

［17］张继龙，甄蜀春，曹鹏，等.实验数据的曲线拟合方法及其应用［J］.测试技术学报，2003，17（3）：255－257.

［18］Hamilton J D.Time Series Analysis［M］.Princeton：Princeton university press，1994.

［19］周长锋，龚日朝，肖国安.基于傅里叶级数的自然灾害损失预测模型研究：以湖南省自然灾害经济损失预测为例［J］.中国安全科学学报，2009，19（8）：5－9.