基于q-贝塞尔近似曲面的地形渲染算法

高艺　裘杭萍　罗健欣　吴波

地形渲染是三维地形仿真研究最重要的内容之一.数字高程模型(Digital elevation model,DEM)[1]作为三维地形可视化的一个重要数据来源,是实现地形渲染的基础支撑.

当前DEM数据主要有两种表示方法:不规则三角网(TIN)和格网(GRID).TIN能用较少的三角形表示地形的高细节,但由于三角网的不规则性带来的存储困难,使其难以表达多分辨率地形.

格网DEM是以二维数组的形式存储数据,每个数组包含一个高程值.因其数据结构简单,易于更新等优点成为了当前比较常用的一种数据格式.

随着地理数据获取技术的发展,一方面,DEM自身的数据量日渐庞大,给计算机实时渲染三维地形场景带来了极大的困难[2];另一方面,在地形渲染时,存储空间大小随着分辨率的增加呈指数级增长.为了减少计算机图形硬件的数据处理量,需要寻找一种能够减少计算机实时处理数据量的方法,这对于大规模地形可视化系统有着重要的意义.

传统的静态渲染算法已经不足以处理地形的实时渲染问题.目前,相关的研究主要集中在地形的LOD(Level of Detail).Lindstrom提出了连续LOD(Continues LOD,CLOD)技术,将地形分块并按精度需求调用不同的块来渲染整个场景,减少了实时渲染的地形网格数量,提高了实时渲染的效率[3].

Duchaineau在CLOD算法基础上提出了一种基于二叉树模型的ROAM(Real-time Optimally Adapting Meshes)算法,该算法以自顶向下的方式构建二叉树,随视点的移动,动态地更新各区域的LOD级别[4].Zhao等基于ROAM算法结合四叉树模型提出了一种修正的LOD技术[5].

Gobbetti等提出的P-BDAM[6](Planet sized batched dynamic adaptive meshes)和C-BDAM[7](Compressed batched dynamic adaptive meshes)算法处理LOD渲染并采用了小波变换的数据压缩.

Marc Treib提出一种稀疏小波变换算法[8]能达到较高的压缩比.小波变换算法不使用传统的几何处理的方式去改变地形网格,误差率低,但是算法涉及复杂的编解码运算.

本文在基于四叉树的LOD算法基础上,提出了一种高效的基于表面近似的渲染方法.这一方法是用近似轮廓取代格网来表示地形,再通过q-Bernstein多项式将离散近似轮廓拼接成G1-连续曲面.相较于传统的DEM渲染方法,本文算法不需要复杂的编解码过程,直接用参数映射生成的连续平滑表面优化了DEM数据,节省了系统存储空间;同时,本文算法渲染时不需要加载全部的DEM数据,极大地提高了渲染效率.

1　近似轮廓

近似轮廓的概念在文献[9]中被提出,用于存储体素数据.这个轮廓为几何模型定义了一系列的平行平面,如果轮廓能够很好地近似原始几何,即用平面来取代原始几何.这一方法对具有较多平坦表面的场景有很好的压缩性能.受这一思想启发,我们将近似轮廓用于地形渲染中,用近似轮廓取代格网来表示地形.

如图1所示,在一个四叉树结构中,首先判断地形变化的总趋势,用整个地形DEM数据计算最佳匹配平面,然后沿着匹配平面的法线方向计算最大平面和最小平面,这两个平面即为近似轮廓的上界和下界.在地形渲染时,当近似轮廓可以很好地近似原始几何时,如图中黑色线框区域,无论分辨率如何增加都只用近似轮廓来代替.

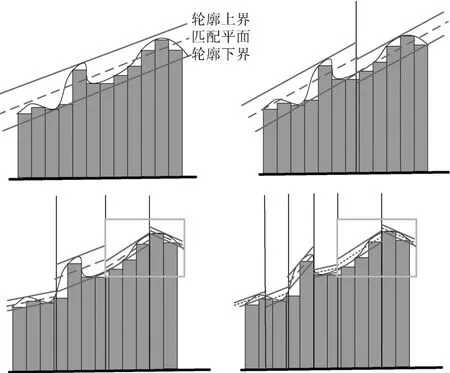
图1　使用近似轮廓表达DEM数据

利用特征值最小二乘平面法来构造DEM的最佳匹配平面.DEM数据中的2D点像素坐标为用齐次坐标表示为P2=R3−(0,0,0)是二维映射空间.一个3D平面用齐次坐标表示为:

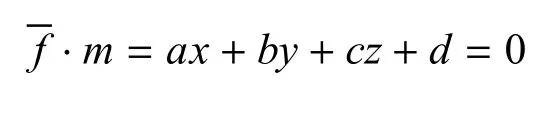
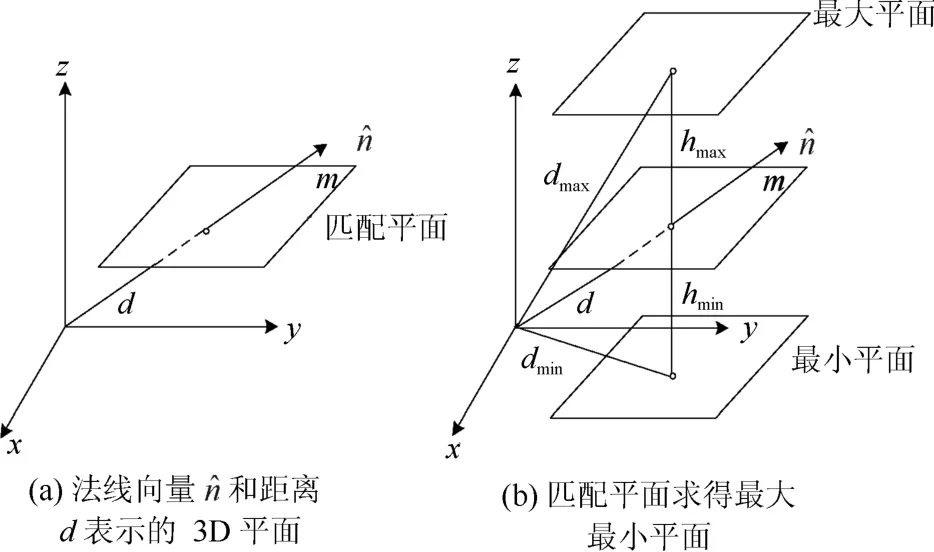
图2　平面示意图

给定DEM中一组n个点P={P1,P2,P3,···,Pn},(xi,yi,zi)≡Pi.计算矩心则定义一组点Q为相对于矩心center的DEM点,要获得最佳匹配平面,在条件a2+b2+c2=1约束下,满足最小.利用拉格朗日乘数法求函数极值构成特征值方程:

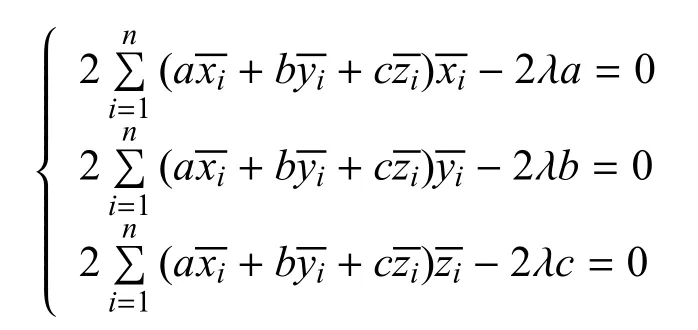
由文献[10]的推导可得:

令M=即为e的最小特征值,最小特征值对应的特征向量即为平面方程的参数a,b,c.

给出点到匹配平面的最大最小距离:

则,原点到最大最小平面的距离为:

求得近似轮廓平面为:

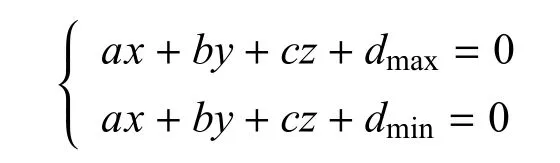
实际情况中,DEM数据在形成和传输过程中会引入多种噪声,噪声往往表现为或大或小的极值.如果不考虑噪声的影响,将会导致获得的匹配平面产生偏差,算法将不具有鲁棒性.因此,在生成匹配平面前需进行DEM的去噪操作.

2　近似轮廓的曲面连续

上述离散的近似轮廓在渲染时会出现不同程度的地形裂缝问题.为解决这一问题,本文引入q-Bernstein多项式[11]将离散近似轮廓拼接成G1-连续曲面.

为每一个匹配平面定义一个离散函数f(向量形式F):

其中,V为平面顶点集,定义一个连续函数f′,如果f′(V)=f(V)则f′为f的插值.给出一个权值因子是一个q-Bernstein多项式,与标准的Bernstein多项式相比,表达式中含有一个可调控形状的参数值q.其定义如下:

其中,参数q为正实数,

当n≥i≥1且r=0时,值为1,否则值为0.当q=1时,即简化为一般的二项式系数.

根据文献[12-13],定义含有两个张量积形式的n×m次q-B´ezier曲面为:

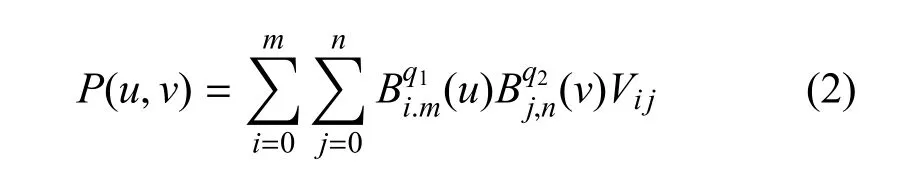
其中,Vij为控制顶点,和是参数为q1和q2的q-Bernstein多项式.

定理.P1(u,v)和P2(u,v)为n×m次张量积q-B´ezier曲面,{pi,j}和{ri,j}分别为其q-Bernstein多项式控制点矩阵,P1(u,v)和P2(u,v)拼接达到G1-连续的充要条件为满足式(3)和式(4):

且拼接边界上u的偏导数对所有的v都有

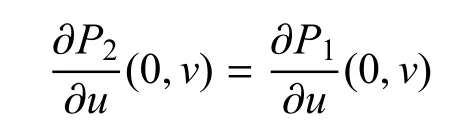
即

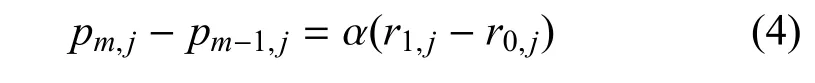
α为大于0的常数.

证明.将式(2)转换为标准B´ezier曲面P′(u,v),为其标准Bernstein多项式控制点矩阵.式(2)可写成

由文献[13]可知,q-B´ezier曲面和标准B´ezier曲面存在如下的矩阵变换关系:

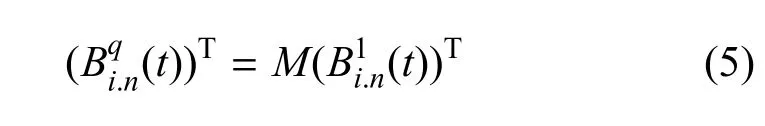
矩阵M有元素:

mi,j=s(n,j)为生成函数的系数,满足:(1+t)(1+[2]t)···(1+[n]t)=详细的公式推导过程请参见文献[13].

由式(5)推出式(4)有如下的转化公式:

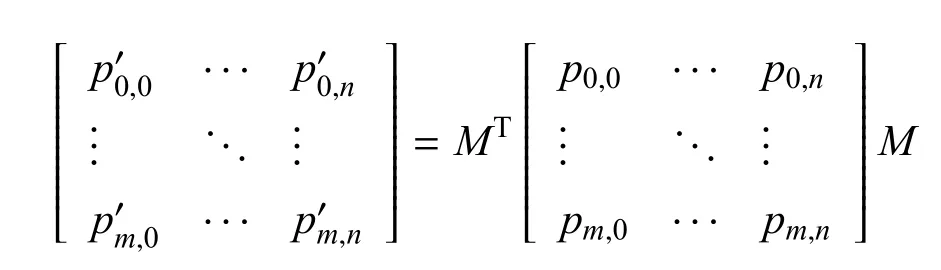
由B´ezier曲面的仿射不变性可知,式(2)和式(3)成立.

因此,本文通过q-B´ezier曲面可以实现将离散近似轮廓拼接成G1-连续曲面,从而消除地形裂缝.

3　算法结果

本文用C++与Cg语言实现了本文算法,并在微软Window XP系统上运行.机器CPU为Intel Core TMi7 950(3.07GHz),内存3GB.显卡为NVGF GTX 480,显存1536MB.实验数据使用一为Puget Sound数据集.二为整个亚洲地区的Google 19层纹理数据集及S高程数据,数据块的调度使用文献[14]的屏幕误差公式:

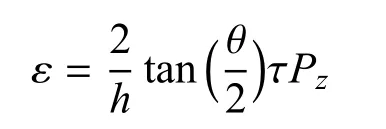
式中,h为视口的像素高度,θ为垂直视野角,τ为屏幕误差容忍,Pz为相机深度,ε为世界空间误差容忍.在本文实验中,屏幕误差设置为2/3像素.

3.1　存储及渲染效率对比分析

将Puget Sound数据集比较不同的分辨率下与文献[15]提出的地形压缩存储算法进行存储量的对比(每个高程值用一个2字节的无符号整型数来存放.从表1可以看出,本文算法在低分辨率时比文献[15]的存储量大,因为四叉树的剖分会产生更多的节点,但随着分辨率的不断增加,本文算法只存储近似轮廓即可,四叉树将不再进行递归剖分,分辨率越大,存储优势越明显.

表1　存储量对比结果

图3显示了本文算法的渲染结果,可以看出算法可以获得较高质量的渲染平面地形.

图3　场景截图

将本文算法与经典的Chunked LoD[16]进行渲染效率的对比.平面分辨率为4096×4096的Puget Sound数据集,窗口大小为1024×768.帧速率公式[17]为:

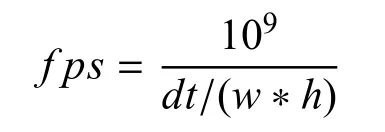
式中,dt为帧时间,w∗h为屏幕分辨率.如图4所示,图中横坐标为渲染过程中的时间记录,纵坐标为记录的帧速率.Chunked LoD方法在渲染过程中为了避免裂缝的产生,会强制添加过渡三角形来填补块间裂缝,造成网格数量的增加,从而影响渲染效率.本文算法的平均帧速率大约为102.334fps,而Chunked LoD的平均帧速率大约为86.349fps,由此可见本文算法具有更高的渲染效率.

3.2　裂缝消除效果

图5显示了用本文方法不使用q-B´ezier曲面渲染和使用q-B´ezier曲面渲染的不同效果.不使用q-B´ezier曲面时,能从图5(a)中看到明显的裂缝,而使用q-B´ezier曲面后,这样的问题得到了明显的改善(图5(b)).

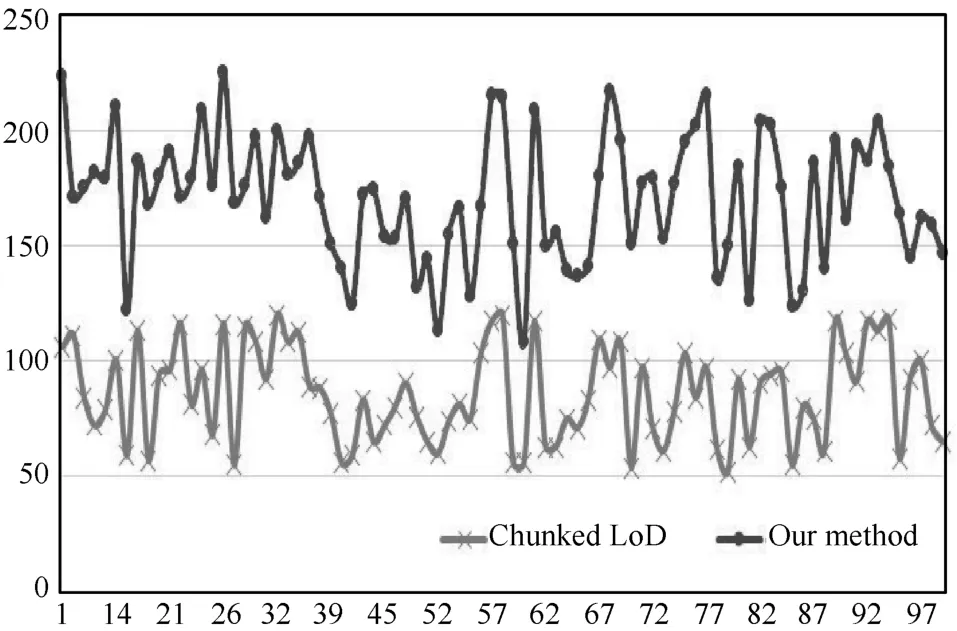
图4　光线投射渲染效率对比

图5　图像比较

4　结论

本文提出了利用近似轮廓取代格网来表示地形的算法,并将离散近似轮廓通过q-Bernstein多项式生成了G1-连续的q-B´ezier曲面,避免了离散近似轮廓在渲染时带来的裂缝问题.实验结果验证了本文算法.下一步研究将该算法移植到GPU中,使其分担CPU中数值计算的任务,从而提高渲染效率.

1 TAO Y,YANG X,TANG G,et al.Primary studies of local shape correction of coarse DEM based on 3D terrain features[C]//International Conference on Geoinformatics.IEEE,2010:1−5.

2 ZHANG R H.Real-time optimization technology and its application in terrain rendering[C]//International Congress on Image and Signal Processing.IEEE,2011:1349−1352.

3 LINDSTROM P,KOLLER D,RIBARSKY W,et al.Real-time,continuous level of detail rendering of height fields[C//Proceedings of the 23rd annual conference on Computer graphics and interactive techniques.ACM,1996:109−118.

4 DUCHAINEAU M,WOLINSKY M,SIGETI D E,et al.ROAMing terrain:real-time optimally adapting meshes[C]//Proceedings of the 8th Conference on Visualization’97.IEEE Computer Society Press,1997:81−88.

5 ZHAO Y,MA Y.A modifieLOD Terrain Model Based on QuadTree Algorithm[C]//InternationalJointConferenceonComputationalSciences and Optimization.IEEE,2009:259−263.

6 CIGNONI P,GANOVELLI F,GOBBETTI E,et al.Planet-sized batched dynamic adaptive meshes(P−BDAM)[C]//IEEE Visualization Conference,2003:20.

7 GOBBETTI E,MARTON F,CIGNONI P,et al.C-BDAM–compressed batched dynamic adaptive meshes for terrain rendering[J].Computer Graphics Forum,2006,25(3):333−342.

8 TREIB M,REICHL F,AUER S,et al.Interactive Editing of GigaSample Terrain Fields[C]//Computer Graphics Forum,2012:383−392.

9 LAINE S,KARRAS T.Efficient sparse voxel octrees[J].IEEE Transactions on Visualization and Computer Graphics,2011,17(8):1048−1059.

10官云兰,程效军,施贵刚.一种稳健的点云数据平面拟合方法[J].同济大学学报(自然科学版),2008,36(7):981−984.

11 ORUC¸H,PHILLIPS G M.q-Bernstein polynomials and B´ezier curves[J].Journal of Computational and Applied Mathematics,2003,151(1):1−12.

12 ZHOU B,SONG L,LI J.Quasi rational B´ezier curves with shape parameter[J].Journal of Residuals Science&Technology,2016,13(7):143.1−143.6.

13 HAN L W,CHU Y,QIU Z Y.Generalized B´ezier curves and surfaces based on Lupa q-analogue of Bernstein operator[J].Journal of Computational and Applied Mathematics,2014,261:352−363.

14 COHEN J D.Appearance-preserving simplificatioof polygonal models[M].Chapel Hill:The University of North Carolina at Chapel Hill,1998.

15白建军,闫超德.基于二叉树的多分辨率地形数据压缩存储[J].西北大学学报(自然科学版),2010,40(6):1088−1092.

16 ULRICH T.Rendering massive terrains using chunked level of detail control[C]//Course Notes of Computer Graphics Annual Conference Series,SanAntonio,ACM,2002.

17 WINGERDEN T V.Real-time ray tracing and editing of large voxel scenes[D].Utrecht:Utrecht University,2015.