基于电阻法的持水率测量方案
冯蒙, 余厚全, 文荣辉, 秦民君, 陈强, 段银鹿
(1.长江大学电子信息学院, 湖北 荆州 434023; 2.中国石油集团测井有限公司, 陕西 西安 710077)
0 引 言
原油持水率是油田开发中的一个重要决策数据[1]。目前中国油田高含水、低产液的大斜井和水平井居多,亟待研发适用于高含水、低产液、泡状流油井的阵列式持水率测井仪器。由于油水电阻率差异很大,基于液体电阻测量流体的持水率是一种可行的方法。为此,开展了相应的研究[2-3],但所提出的方法和仪器在阵列化和减少矿化度的影响方面不同程度地存在着需要解决的问题。由于目前中国没有研制出成熟的适用于高含水的阵列电阻持水率检测仪器,主要通过引进Sondex公司于2009年推出的阵列电阻式持水率成像测井仪(RAT)[4]来满足中国油田的生产需求。因此,研发具有自主知识产权的阵列电阻持水率仪具有重要意义。本文根据电阻的测量原理,详细分析了电阻传感器的电学模型,通过选取合适的频率和测量时刻点,减小了双层电容和分布电容的影响;在此基础上,设计基于双极性脉冲法的电阻测量电路,达到了分辨油水两相泡状流的油水属性要求;提出基于单位时间实测流体电阻二值化样本统计估计持水率的计算方法。实验结果表明,通过上述方案检测估计的流体持水率可以反映流体含水率的变化,并通过调整电阻二值化阈值校正矿化度的影响。
1 基于流体电阻的持水率检测原理
根据持水率的定义(油井单位流体截面上水所占的面积),油井截面P点的局部持水率hp可以定义为以P点为圆心、以一个小r值为半径的微圆面上水所占面积与微圆总面积之比,即
(1)
式中,Sp表示以P点为圆心、以r为半径的微圆总面积;Spw表示在该微圆面上水所占的面积。在高含水、低产液油井中,流体的形态一般是呈油水两相分离的泡状流体或分层流体。当微圆的半径r远小于泡状流体的半径时,hp要么接近100%,对应于微圆面上接近为全水;hp要么接近0%,对应于微圆上接近为全油。上述条件下持水率具有明显的离散性,hp的直方图分布具有相隔较远的双峰特征,它反映了油水两相分离的泡状流的流动特征。因此,对于泡状流而言,单次测量的持水率没有工程意义。为获得合理的、具有实际工程意义的持水率值,可采用2种方法实现。
方法一:对该点第i段时间内M次测量的持水率hpi1,hpi2,…,hpiM进行统计平均,作为该点在第i段时间的持水率值,即
(2)
方法二:对该点第i段时间内M次测量的持水率hpi1,hpi2,…,hpiM进行二值化处理,记为B[hpik],k=1,2,…,M。如果hpik≥Th,则B[hpik]=1,否则,B[hpik]=0,从而B[hpik]反映了流体的油水属性。Th为预设的油水属性分界的持水率阈值。因此,该点在第i段时间的持水率值可表示为
(3)
即对每次测量的hpik,k=1,2,…,M,通过B[hpik]判断该次微圆面上流体的油水属性,统计出该时间段被判为水性流体的次数占总检测次数M的比例。
实际应用中,直接测量微圆面上的持水率非常困难。考虑到油与水的电阻值差异很大,特别是当矿化度存在时两者的差异更大[见图1(a)所示的油水电阻值分布图],因此通过测量微圆面周边上相距最大的2点之间的电阻作为判别微圆面上流体油或水的属性参数。可采用基于流体局部电阻的持水率检测方法,原理如图1(b)所示。具体检测步骤:
(1) 在油井截面P点,放置一个电极距离为2r的探针式电阻传感器。
(2) 在该点第i段时间内进行M次流体电阻测量,依次得到电阻为Rpi1,Rpi2,…,RpiM。
(3) 基于检测到的M个流体电阻值Rpik,k=1,2,…,M,通过二值化处理对流体的油水属性进行判断,如果Rpik≥TR,B[Rpik]=0,流体属性为油;如果Rpik (4) 按式(3)进行计算,其结果作为油井截面上局部P点第i时间段的持水率估计值。 图1 油水电阻分布频度图和持水率检测原理图 电阻测量的一般方法如图2(a)所示。信号源通过一限流电阻Rf施加到被测电阻(电阻传感器)上,测量被测电阻两端的电压和流经被测电阻的电流,即可求得被测电阻值。为避免直流信号源激励时传感器电极极化,激励信号采用双极性脉冲信号。 但是,采用上述方法进行流体的电阻测量时,电阻传感器等效电路模型并不是一个纯电阻。文献[5]、文献[6]指出:由于液体电极化作用,电阻传感器在液体测量池中的一般电路模型等效为一个电阻与电容的串并联电路,液体电阻测量池和电阻传感器等效电路如图2(b)和2(c)所示。Rx为电极间被测液体的电阻;Cp为液体的电解质电容和电极引线的分布电容之和,一般电解质电容远小于电极引线的分布电容,因此,Cp大小主要与电极的结构有关;Cx为双层电容,它反映了交流信号激励探针时,电极表面交替吸引正负离子,离子在平衡位置处往复振动所对外呈现的电容效应,其大小与传感器结构和被测溶液有关。 图2 电阻测量电路及电阻传感器等效电学模型 为避免或减小Cp和Cx对测量Rx的影响,最佳的情况就是在分布电容Cp近似开路和双层电容Cx近似短路的时刻进行测量。 对于探针式电阻传感器,Cp通常在pF数量级。设限流电阻Rf=10 kΩ,Cp的充放电时间常数τp=Rf‖Rx×Cp,其最大值τp,max=Rf×Cp,则τp的范围为1 ns~10 μs。当充电时间为4τp时,可以认为Cp已经充电完成,达到稳态,Cp相当于开路。为实际了解Cp对测量Rx的影响,实验观察在10 kHz[7]双极性对称方波激励下,且被测液体为纯油(Rx最大,相应的τp亦最大),实验探针式电阻传感器两端的电压波形如图3(a)所示(黄色为激励信号,蓝色为传感器两端的电压信号)。由图3(a)中波形可见,即便是在τp最大时,传感器两端的电压跳变的暂态过程也不明显。因此当双极性激励信号的频率在10 kHz或10 kHz以下时,实验探针式电阻传感器的等效模型可简化为被测电阻Rx与双层电容Cx的串联,可以不考虑分布电容的影响[见图3(b)]。 图3 传感器在纯油中电压波形及简化的电学模型 Cx对应的时间常数为τx=(Rx+Rf)Cx,随着被测液体的导电性不同而变化,进而导致传感器两端的电压的暂态过程也发生改变。Cx一般在μF数量级[8],但对于探针式电阻传感器,其Cx还要小很多,在nF数量级,对测量结果的影响要显著得多。为避免Cx对Rx测量影响,在双极性脉冲信号对其进行正反向充电期间,在每半周期找到Cx两端压降为0(Cx短路)的那一时刻进行传感器两端的电压和电流测量,这时测量到传感器两端的电压值即为被测电阻Rx两端的电压值。 在周期为T、幅度为E的双极性脉冲信号激励下,传感器两端的电压U0(t)在半个周期的稳态响应如式(4)所示,U为激励源电压(正脉冲激励下U=E,负脉冲激励下U=-E)。 (0≤t≤T/2) (4) 可以证明在半周期内,存在唯一的时刻点t0,使得U0(t0)满足 (5) 即传感器两端的电压等于被测电阻两端的电压。这时测量即消除了Cx对Rx测量的影响。将式(5)带入式(4)中,可得 (6) 由式(6)可知,激励信号选定后,t0只与Cx和Rx有关。取Cx为10~1 000 nF,Rx为1 kΩ~10 MΩ,用Matlab绘制t关于Cx和Rx的二维曲面[见图4(a)]。 图4 不同双层电容和溶液电阻下相关量的仿真图 % (7) 鉴于被测流体电阻动态在5 000 Ω~15 MΩ的动态范围,采用双极性脉冲激励、同时测量传感器两端电压和流经传感器电流的方案,以消除激励源不稳定引入的误差,扩大测量的动态范围。电阻测量电路如图5所示。 测量电路中,运放U3、取样电阻R2组成电流检测电路。U3为精密电流电压转换器,可将流过传感器的电流值转换为电压值。传感器的负端接在了运放U3的反相端,实现“虚地”,避免了采用公共地时电流的测量误差。 限流电阻R1、运放U1和U2构成电压测量电路。U1为仪表放大电路,选择具有低偏置电流的U2和外围电容电阻组成电压跟随电路,获取传感器负端的电压值,U1和U3的输出信号为V01、V02,得传感器电阻值 (8) 为减小双层电容和分布电容的影响,采用延时同步采样技术。通过控制模拟开关(SW1/SW2/SW3/SW4)的快速断开和闭合,在每个半周期开始后延时25 μs分别采样传感器两端的电压值和流经传感器的电流值,分别依次保存在后续4个U4、U5、U6和U7并行的采样保持器,由AD转换器将它们转换为数字量。 图5 电阻测量电路 由于双极性激励电压的对称性,且在一个周期内的2个正负半周期采用间隔很短只有50 μs,可以认为其间溶液的电阻没有变化,因此可以取两者的电压差值和电流差值作为电压值和电流值,以便减小检测系统的直流漂移和低频干扰。故由式(8)可得到溶液的电阻值的计算公式 ⑵Cox单因素分析结果表明:肿瘤浸润深度、淋巴结转移、TNM分期、分化程度、NLR、PLR、MLR、NWR、LWR、MWR是影响胃癌患者总体生存期的不良预后因素(P<0.05)。 (9) 式中,ADC1、ADC3分别是正脉冲激励时电压、电流信息对应U4、U6的输出;ADC2、ADC4分别是负脉冲激励时电压、电流信息对应U5、U7的输出。 为验证上述方案的测量精度,利用设计开发的检测电路分别对1、5.1、10、51、100、510 kΩ和1、5.1、10 MΩ共9组标准电阻进行2 000次测量,计算每组数据的最大相对误差。结果表明,当Rx在1~100 kΩ范围时,最大测量误差小于2%;当被测电阻在100 kΩ~1 MΩ范围时,最大测量误差小于4%;当被测电阻大于1 MΩ时,最大测量误差小于13%。这种随着被测电阻值增大测量误差增大的原因是由于被测电阻增大导致被测电流值减小,电流检测电路中微小干扰就会导致按式(9)计算被测电阻时误差被放大。 为验证该方案的可行性,在油水两相泡状流模拟实验装置中,用该测量系统进行了流体电阻的测量实验。实验井筒直径100 mm,流体流量为2 m3/d,实验用油为0号柴油,实验用水为自来水,分别设定含水率为0%、65%、80%、100%。每秒检测10次流体的电阻值,并统计一段时间内液泡电阻值的直方图分布(见图6)。 图6 油水两相流体液泡电阻值分布直方图 含水率为0%时,实测的液体电阻值约为11 MΩ。结果表明,在相应的直方图中,全部液泡的电阻值都100%地分布在5 MΩ以上。当含水率为65%时,电阻的直方图呈两极化分布。其中,一分布区阻值在100 kΩ以下,其液泡约占全部样本的54%;另一分布区在1 MΩ以上,约占全部样本的14%;100 000~1 MΩ内液泡的比例为32%。当含水率为80%时,阻值在100 kΩ以下的液泡比例增加,阻值在1 MΩ以上的液泡比例减小。当含水率为100%时,实测的液体阻抗值约为18 kΩ,液泡的阻值100%的分布在50 kΩ以下。 从直方图中可以看到,在流体非全油和非全水条件下,阻值呈两极化分布,但也存在一部分中间阻值的测量值。这是因为探针2个电极之间存在一定的距离,电路进行采样测量的瞬间,流经探针式电阻传感器2电极间的流体并非一定是全油或者全水,而是油水相间时,其比例在(0,1)开区间变化,或者说流经探针2电极间液泡的直径小于间距,就出现了介于油水两者电阻之间的阻值。如果将这部分非油非水的电阻值纳入统计,就会造成一定的偏差。因此稳健的处理方法是设定上下双阈值,剔除电阻值介于上下阈值之间的测量样本。 一般而言,油电阻值(10 MΩ)大约为水电阻值(15 kΩ)的660多倍,考虑到不同油以及不同水电阻值的差异性,下阈值一般选在水的电阻值的2~4倍之间,约在30~60 kΩ之间;上阈值选在油的电阻值的1/3~1/2之间,约在3~5 MΩ之间。将阻值小于下阈值和大于上阈值的样本挑选出来纳入持水率估计的样本集。 表1为上下阈值分别设定为50 kΩ和5 MΩ时估算的流体持水率,其结果表明计算出的持水率基本上能够反映含水率的变化。 通过对比不同矿化度下阻值分布直方图发现: 表1 持水率测量数据 图7 不同矿化度的电阻值分布柱状图 (1) 电阻值两极化分布的形态依然明显存在。 (2) 当矿化度由0 g/L→2 g/L→4 g/L增加时,电阻值分布整体向低电阻值方向偏移,低电阻值样本的频度大大增加。这是由于盐溶于水,而不溶于油,随着矿化度的增加,水的电阻值明显减小,当流经传感器2电极间的流体为水或油水相间的流体时,其电阻值分布向低阻值方向偏移。 为避免矿化度导致电阻值分布向下发生偏移对持水率估计的影响,应根据矿化度相应地调整上下阈值。表2给出了含水率为65%的流体在不同矿化度情况下选择不同上下阈值的处理结果。为了获得相对一致的持水率估计结果,在矿化度分别为2 g/L和4 g/L时,选择的上下阈值分别为50 kΩ和5 kΩ,相对于0矿化度时的电阻阈值分别减小了1/100和1/10。 表2 不同矿化度的持水率测量数据 (1) 对于井下油水两相分离的泡状流,探针式电阻传感器检测流体电阻的直方图呈两极化分布。 (2) 基于流体电阻值采用上、下双电阻阈值判别,可以相对很好地识别流体的油水属性。 (3) 通过统计一段时间内检测的水性样本数占该时间段油性和水性样本总数的比例作为持水率估计,可以很好地反映含水率的变化。 (4) 当矿化度存在时,通过调整上下阈值可以避免矿化度对持水率估计的影响。 参考文献: [1]郭海敏. 生产测井导论 [M]. 北京: 石油工业出版社, 2010. [2]ANDREUSSI P, DONFRANCESCO A D, MESSIA M. An Impedance Method for the Measurement of Liquid Hold-up in Two-phase Flow [J]. International Journal of Multiphase Flow, 1988, 14(6): 777-785. [3]胡金海, 刘兴斌, 刘继新, 等. 阵列电导探针流体成像仪在油水两相下的实验 [J]. 石油仪器, 2013, 27(1): 18-20. [4]Resistance Array Tool 12-Sensor Springbow, 111/16in, UltrawireTMOperational & Maintenance Manual [Z]. 2012. [5]傅卫卫. 工业水处理过程中电导率测量方法的研究 [J]. 浙江大学学报, 1999, 33(2): 204-208. [6]张敏. 一种新型工业电导信号测量仪的研制 [D]. 浙江: 浙江大学, 2005: 9-11. [7]李雷, 刘兴斌, 胡金海, 等. 阻抗含水率计激励源电路动态特性研究 [J]. 石油仪器, 2010, 24(3): 17-19. [8]BARD AJFAULKNER L R. 电化学方法原理与应用 [M]. 邵元华, 等译. 北京: 化学工业出版社, 2005.
2 基于双极性脉冲激励的流体电阻测量方法



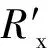
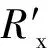
3 基于双极性脉冲激励的流体电阻测量电路

4 实验数据及分析
4.1 标准电阻测量实验
4.2 零矿化度条件下不同含水率流体电阻的测量实验

4.3 不同矿化度下相同含水率的持水率测量实验

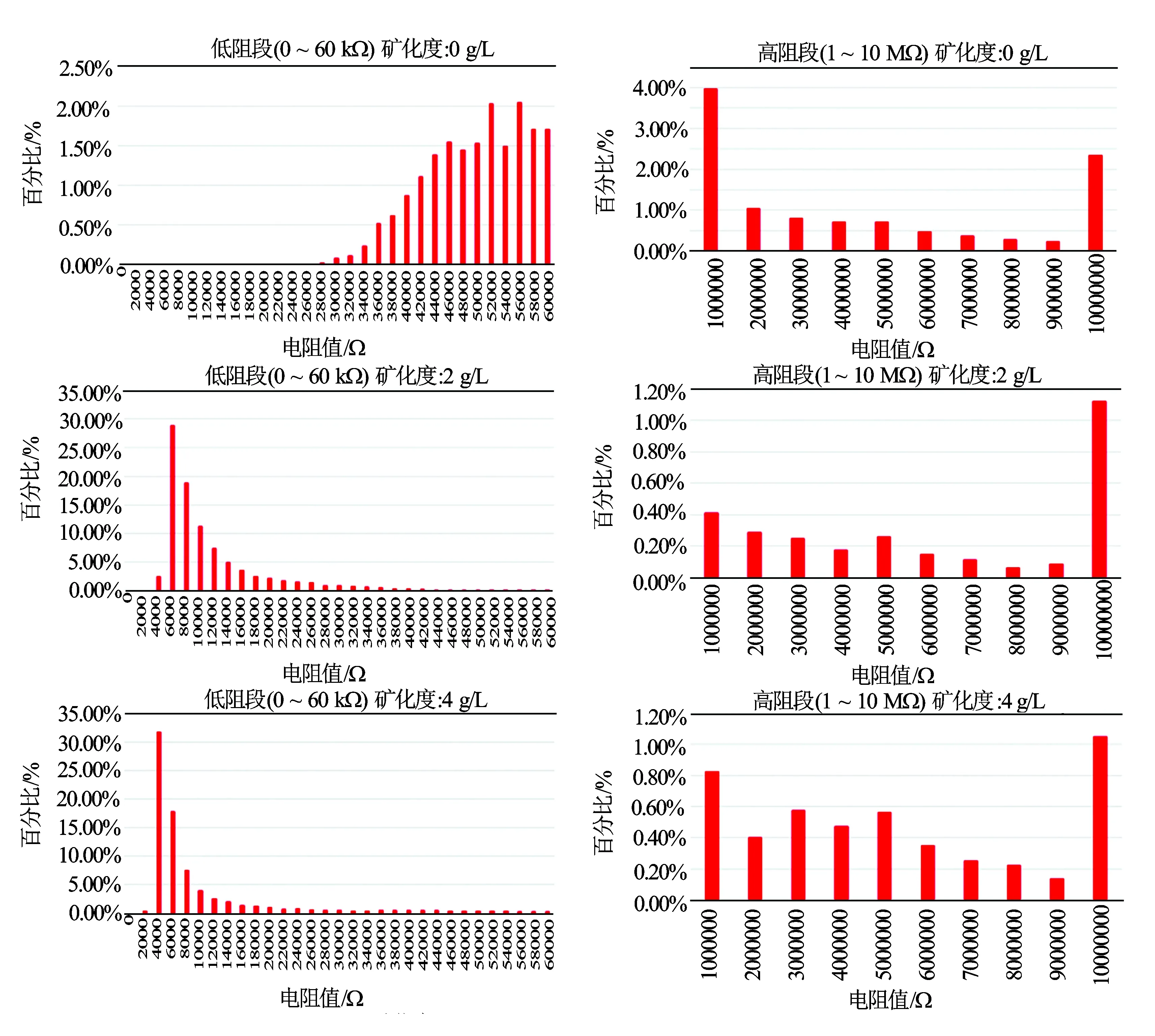

5 结 论

