基于Lorentz函数的稀疏约束RBM模型的算法研究
邹维宝,于昕玉,麦 超
ZOU Weibao1,YU Xinyu1,MAI Chao2
1.长安大学 地质工程与测绘学院,西安 710054
2.广西壮族自治区遥感信息测绘院,南宁 530023
1.School of Geological Engineering and Surveying,Chang’an University,Xi’an 710054,China
2.Guangxi ZhuangAutonomous Region Remote Sensing Information Surveying and Mapping Institute,Nanning 530023,China
1 引言
人工神经网络[1-4](Artificial Neural Network,ANN)作为一种运算模型,是通过模仿生物神经网络的功能和结构,由大量的人工神经元之间相互连接组成,是实现人工智能的先导性技术之一。1986年Hinton等人提出了一种反馈式神经网络模型——玻尔兹曼机(Boltzmann Machine,BM)[5],用来改进确定性神经网梯度下降法学习目标特征时容易陷入局部极小点的问题。BM是由随机神经元之间全连接组成的,它采用无监督方式学习,对于特征较复杂的数据,该模型具有很好的学习能力,但是网络训练时间较长。由于BM估计数据分布具有困难性,所以Smolensky[6]引入了受限玻尔兹曼机(RBM)。RBM由可见神经元层和隐神经元层组成,但是层内无连接,层间相连接,这一限定使得相比一般玻尔兹曼机更高效的训练算法成为可能,直接计算依赖数据的期望值变得容易。自RBM的基本模型被提出以来,尤其是基于CD的快速学习算法[7-8]被提出之后,RBM受到了前所未有的关注,特别是在图像处理领域。RBM具有强大的无监督学习能力,能够从大量的数据中学习到有用的特征表示,尤其适合提取图像的特征信息[9]。另一方面,视觉是大脑获取外界信息的主要来源,视觉系统对所感知的图像特征以稀疏编码的形式进行描述,这既对繁杂冗余的信息提供了简单表示,又利于上层传感神经元抽取刺激中最本质的特征,因此将稀疏这一概念引入到RBM中,目的是学习到更有效的特征信息。由于RBM是基于能量的模型,在RBM中添加稀疏约束符合生物进化普遍的能量最小经济策略,能够学习到原始数据的稀疏表示,提高其特征提取性能。稀疏RBM可通过模拟人类视觉系统工作原理,表征图像数据的稀疏表示,展现了其强大的特征学习的能力,利用RBM获取稀疏表示已经成为模式识别乃至机器学习的一个热点方向。
关于稀疏RBM的典型算法有基于误差平方和稀疏惩罚因子的稀疏RBM[10](Sparse Restricted Boltzmann Machine,SRBM)、基于稀疏组的稀疏RBM[11](Sparse Group Restricted Boltzmann Machine,SGRBM)和基于率失真理论的稀疏RBM[12](Sparse-Response RBM,SR-RBM)。因为每个隐单元的激活概率有可能相同也有可能不同,因此SRBM给每个隐单元赋予相同的平均激活概率并非最优策略;SGRBM的隐单元分组方式不明确且分组含义模糊,同时该算法无分组依据;SR-RBM无法得到最优失真度量。因此,有必要对稀疏RBM进行进一步的研究。
将Lorentz函数稀疏约束,已经在多个领域得到广泛的应用。例如,边缘检测、高分辨率Fourier频谱估计[13]、视觉稀疏分析、图像建模以及SAR影像特征增强[14]等方面,将Lorentz函数作为稀疏约束正则项都有非常好的理论和实践效果,故在RBM中增加Lorentz函数稀疏约束以模拟人类视觉信息处理机制,将其作为目标特征提取器。
2 理论基础
RBM是一种具有双层结构的无向图模型[15-16],如图1所示。V为m维可见层,用于输入数据,h为n维隐层,用于提取输入数据的高阶相关特征,均为二值随机变量,vi,hj∈{0,1},W∈Rm×n为可见层与隐层之间的连接权重。RBM是一种基于能量理论的概率模型,对于给定的状态(v,h),其能量函数定义为:
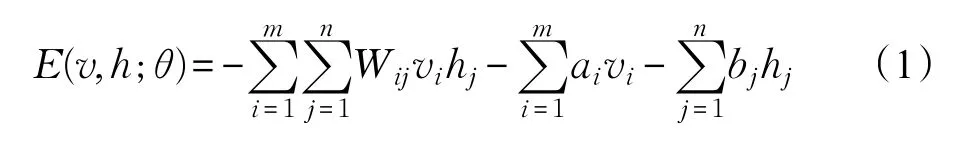
式中,θ={W,a,b}为RBM模型的参数,Wij表示可见单元i与隐单元 j之间的连接权重,ai表示可见单元i的偏置,bj表示隐单元 j的偏置[17]。

图1 RBM基本结构图
RBM的状态符合正则分布的形式,也就是说,给定状态(v,h),可见单元和隐单元的联合分布函数定义为:
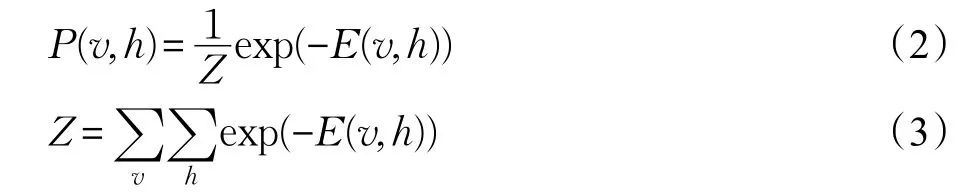
其中,Z为归一化因子。特别的,给定可见单元,隐单元即为独立的伯努利随机变量,此时,第 j个隐单元的激活概率为:

式中,σ(x)=1/(1+exp(x))为Sigmoid激活函数;给定隐单元,可见单元也是独立的伯努利随机变量,此时,第 j个可见单元的激活概率为:

将RBM稀疏约束,即将稀疏编码引入到RBM中,获取输入数据的稀疏表示。从统计学角度来理解RBM稀疏性,就是要求尽可能少的隐单元被激活,而绝大多数的隐单元不被激活,即隐单元的激活概率密度函数的图像同时具有尖峰性和重尾性的特点。目前,比较常用的稀疏分布是广义高斯分布,而Cauchy分布同样具有广义高斯分布特性,故Cauchy分布可作为稀疏先验知识[18]。而具有稀疏分布特性的先验信息,可以使RBM隐单元的激活概率具有稀疏性。
关于RBM的稀疏先验,本文提出采用以下形式的Cauchy先验分布模型:

式中,sh为尺度函数,根据Bayes定理,结合公式(4),可得后验分布为:
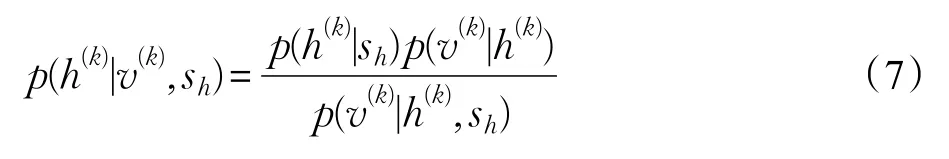
那么提高RBM模型稀疏性的最大后验估计为:

上式等价于以下的最小化问题:

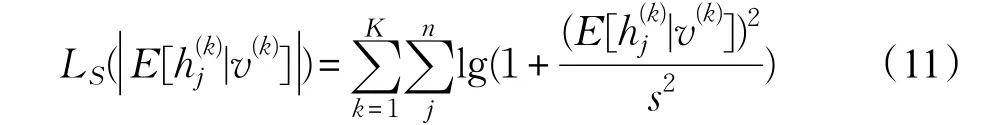
3LRBM模型算法与求解
为了使模型学习得到稀疏表示,需要调整{Wij,ai,bj}使得RBM在训练集上的对数似然函数最大化,并通过稀疏约束获得训练集的稀疏分布。因此,由式(11)可得LRBM模型的目标函数为:

目标函数的前一项为似然度项,后一项为正则化项(稀疏约束项),其中参数λ为正则化参数,反映正则项对于所得到的分布的相对重要性。由上式可见,目标函数在最大化似然度的同时最小化Lorentz稀疏约束函数。
对于目标函数的求解可以用梯度下降法进行求解,但是如果直接使用梯度下降法求解该目标函数中的似然度项,将会大大增加计算复杂度,是不可行的。因此,本文参考文献[10],LRBM训练算法主要是使用CD算法求得似然度项的近似梯度,再用梯度下降法解算正则化项。即给定训练数据,每一次迭代将首先应用CD算法更新模型参数一次,再使用正则化项的梯度值在更新模型参数一次。由于隐单元偏置直接控制着隐单元的激活概率以及稀疏程度,相对于更新所有参数,本文在使用正则化项的梯度值更新参数时只更新隐单元偏置bj。其中,正则化项的梯度计算如下:


4 基于LRBM的DBN模型
2006年,Hinton等人首次提出了由多个RBM堆叠而成的深度结构网络——深度置信网络(Deep Belief Network,DBN)。该结构是目前研究和应用都比较广泛的深度学习结构,其实质是通过构建具有多个隐层的机器学习模型组合低层特征,形成更加抽象的高层来表示属性类别或特征找到数据的主动驱动力量。其动机在于模拟人脑进行分析学习的神经网络,模仿人脑的信息处理机制来解释数据。深度置信网的网络结构如图2所示,其核心思路为:(1)无监督学习用于每一层RBM;(2)每次用无监督学习只训练一层,将其训练结果作为高一层的输入;(3)用自顶而下的监督学习算法去调整所有层。

图2 深度置信网的网络结构
与DBN由一系列RBM单元组成类似,本文构造的稀疏DBN由一系列LRBM单元组成,称之为LDBN。与DBN的学习算法类似,该稀疏DBN的预训练同样可以采用无监督贪婪逐层训练法逐层训练LRBM方式来实现。即在训练过程中,首先训练底层具有稀疏约束的RBM,然后固定本层的参数,并将本层的隐单元激活概率作为下一层带有稀疏约束的RBM的输入,直到最后一层。
5 实验分析
模型的特征提取性能、分类率、稀疏性以及强壮性是评价稀疏RBM模型优劣的主要技术指标,本文接下来将重点以MNIST数据集为训练集对LRBM的性能进行验证,为不失一般性,还以CIFAR-10数据集为训练集做了一些实验。由于LRBM是RBM的改进模型,而SRBM是最典型的稀疏RBM模型,故本章待比较的模型为RBM模型和SRBM模型。

图3 MNIST数据集部分样本
5.1 基于MNIST数据集的实验分析
MNIST手写体字符识别数据集是目前验证深度学习各种算法最常用的数据集之一,该数据集包括0~9的10个手写数字图像,还包含每个图像对应的标签(0~9)以便用于有监督学习的实验;图3显示了MNIST数据集的一部分样本。该数据集每个样本为28×28像素的灰度图像,包括60 000个训练样本和10 000个测试样本。本文从该数据集中随机选取每类2 000个训练样本作为训练样本,并将其分成200组各包括100个样本的小批量数据,从模型的特征提取性能、分类率、稀疏性以及强壮性四方面对LRBM的性能进行检验。
(1)模型的分类率
为了证明LRBM模型所学习到的稀疏表示具有良好的可判别性,首先训练由两层模型堆叠而成的深度结构模型,将RBM、SRBM、LRBM分别作为模型的基本组成单元,将第一个基本单元的输出作为第二个基本单元的输入,分别对其进行训练。其中第一个基本单元的隐单元设置为484,第二个基本单元的隐单元均设为196。然后将每一层LRBM以及其对比算法(RBM和SRBM)的输出作为线性分类器的输入,以线性分类器所得的分类率评价各无监督学习算法的可判别性能。在分类阶段,本节将分别随机选取每类100、500、1 000个样本作为线性分类器的训练数据,而剩下的样本作为线性分类器的测试数据。同时,对于每个模型的输出与每个样本数的组合,都重复训练20个线性分类器,用这20个分类器的分类率的平均值来评价相应模型所学习到的分布的可判别性。
表1显示的是SRBM在不同稀疏惩罚因子下(λ均等于2),不同样本数的分类率。表2显示的是给定尺度参数为0.5的情况下(激活概率为0.5意味着不确定性最大,故设置正则化函数在0.5处有最大的梯度),不同正则化参数下不同样本数的分类率。在与RBM模型算法比较以及训练多层结构模型时,均采用SRBM、LRBM分类率最高情况下的参数。表3显示的是LRBM与其他无监督学习模型在不同样本数下的分类率。
从表1和表2可以看出,在一定范围内SRBM对惩罚因子 p、LRBM对正则化参数λ并不敏感,但对比表1和表2可得LRBM的总体表现要好于SRBM。
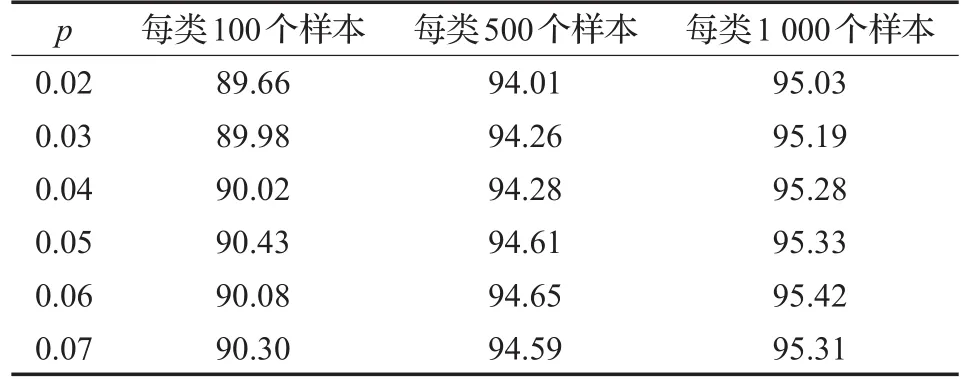
表1 SRBM在不同稀疏惩罚因子下的不同样本数的平均分类率 %

表2 LRBM在不同正则化参数下的不同样本数的平均分类率 %

表3 基于不同样本数的各模型的平均分类率 %
从表3可得,LRBM在不同训练样本数情况下的平均分类率均优于其他无监督学习模型,尤其是在小样本分类方面,LRBM的分类率相对于RBM有不小的提升。
从图4可以看出随着样本数的增加,各模型训练时间也会变长,但是各模型之间相差并不多,即增加正则化稀疏函数并不会对分类时长造成影响。

图4 基于不同样本数的各模型分类所用时间
本节还将深度结构模型中第二层的输出作为线性分类器的输入,得到模型的平均分类率如表4所示。从表4可以看出,经过两层LRBM模型学习所得到的平均分类率依然较RBM、SRBM高,进一步表明LRBM所学习到的特征具有良好的可判别性;同时本实验也在一定程度上证明,增加模型的深度可提高模型的可判别能力。

表4 双层模型第二层输出的平均分类率%
如图5为各双层模型基于不同样本数进行分类所用的时间。与图4类似,随着样本数的增加,各模型分类时长也有所增加但各模型之间所用相差不多。不同的是,双层的无监督模型的分类时长较单层模型有所增加。
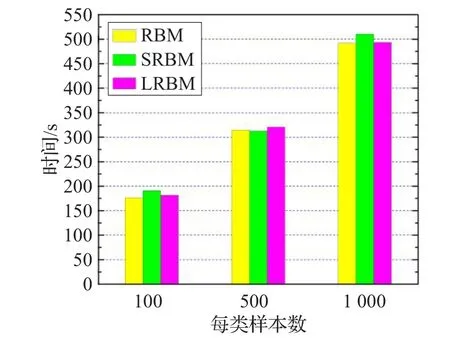
图5 基于不同样本数的各双层模型分类所用时间
(2)基于可视化特征提取评价
为了展示模型学习到的特征的好坏,对之前所学习到的部分特征进行可视化。如图6显示了各模型学习到的部分特征。
从图6可知,RBM模型学习到的大部分特征都是难以名状的,只有少数几个特征稍微具有一定的形状;而LRBM能够学习到的特征更具清晰的轮廓而不是随机的难以名状的构造,可以看出这些特征就是训练样本的局部特征;而LRBM与SRBM相比,两者可视化差别很小。

图6 各模型所学习到的部分特征
(3)稀疏度的比较
为了度量LRBM的稀疏度,本文采用Hoyer提出的稀疏性度量[19]来衡量RBM、SRBM、LRBM的稀疏度,给定D维向量v,则该向量的稀疏度为:

从上式可知,该稀疏度量在区间[0,1],稀疏度越接近于1意味着向量v越稀疏(向量v中等于0或者接近0的元素就越多)。如表5显示了各模型的稀疏度均值。从表5可知,LRBM学习到了关于输入数据的更为稀疏的表示。为了直观地表示稀疏度,图7给出同一张训练图像在各模型中的隐单元激活概率,图8给出了同一数据集在各模型中的得到的激活概率统计直方图。

表5 各模型的平均稀疏度
由图7可知,RBM接近于0的激活概率较SRBM和LRBM少得多,而SRBM和LRBM绝大部分隐单元激活概率非常接近于0。从图7也可以看出RBM学习到的分布明显不是稀疏分布,这从侧面证明了给模型增加稀疏约束项可以促使模型学习到稀疏分布。如果说仅采用图7显示的同一样本的激活概率就说明LRBM由于其他模型不够严谨的话,那么从图8的同一数据集在各模型中隐单元的激活概率直方图可知,LRBM落在区间(0,0.1)的隐单元激活概率数多于其他模型,与此相反的是LRBM落在其他区间的隐单元激活概率数均少于其他模型。由此可以看出LRBM学习到的分布更稀疏。
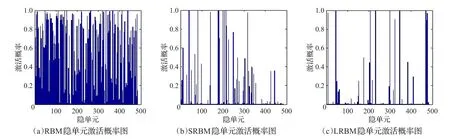
图7 同一图像在各模型中的隐单元激活概率图
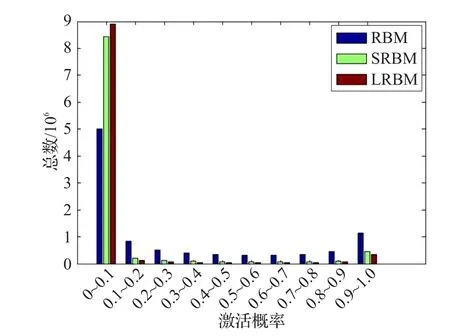
图8 基于同一数据集的各模型激活概率值
(4)模型的强壮性分析
模型的强壮性是指模型在一定(结构、大小)的参数摄动下,维持其他某些性能的特性。以上的实验只验证了各模型的在分类率最高情况下的特定参数值的特征提取性能,为分析模型的强壮性,本节将调节各稀疏约束项的参数,将所得结果作为线性分类器的输入,其中以每类500个样本为线性分类器的训练样本,计算各参数组合的分类率。表6和表7分别显示了SRBM和LRBM在不同稀疏约束参数下的分类率(其中取每类500个样本作为线性分类器的训练样本)。

表6 不同惩罚因子p和正则化参数λ下SRBM的分类率%
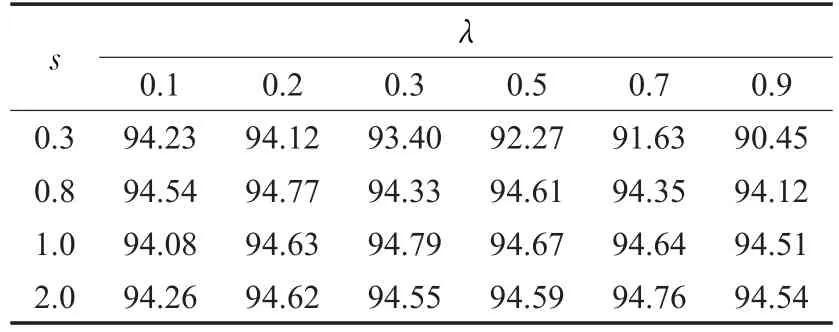
表7 不同尺度参数s和正则化参数λ下LRBM的分类率%
SRBM通过稀疏惩罚项试图将同层所有隐单元赋予相同的平均激活概率 p。在实际应用中,如果将 p值设定的较小,每个隐单元的平均激活概率也较小,如果设置的较大,则不能迫使隐单元学习到原始数据的稀疏分布。从表6可以看出,当 p=0.3时,所得的分类率与未增加稀疏约束项的RBM所得的分类率非常接近;当 p>0.3时,所得的分类率则会降低,这是由于RBM隐单元对MNIST数据集的平均激活水平约为0.3,若设置p>0.3则会迫使隐单元学习到的激活概率值远离0值。
LRBM采用的是与SRBM完全不同的稀疏惩罚方式,由Lorentz函数的导函数可知,LRBM并不是通过稀疏惩罚项迫使隐单元学习到特定激活水平的激活概率,而是根据不同的训练任务学习到不同的稀疏水平。从表7可得,尺度参数s的取值范围较SRBM稀疏惩罚因子的取值范围要大的多;表7中当s=0.3而λ取较大值时分类率有所降低,是因为Lorentz函数的导函数在尺度参数s处取得最大值,因此如果将s设置得较小,当隐单元激活概率降到一定水平时,稀疏惩罚项的梯度值仍然很大,故λ越大分类率越低。
综上,虽然当s取较小值时对λ的取值有一定的要求,但是整体来说LRBM中s的取值摄动对模型分类率影响比SRBM中 p取值对分类率的影响要小得多;由Lorentz函数及其导数形式可知,当稀疏系数X趋近于0时,Lorentz函数及其导函数的取值趋于0,这是符合稀疏约束函数的稳健条件的,而SRBM的稀疏约束项则不符合这一条件,故可得LRBM模型的强壮性要好于SRBM。
(5)基于LRBM的稀疏深度置信网模型的实验分析
目前一个RBM很重要的应用,就是将RBM作为一个单元初始化神经网络[20]。将LRBM代替RBM作为深度置信网的组成单元,初始化深度置信网。本文采用文献[20]中报告的网络结构,即使用LRBM初始化一个784-500-500-2 000的网络,来训练MNIST数据集。初始化阶段,使用MNIST数据集的所有训练数据作为网络的训练样本(与文献[20]相同)。其中尺度函数和正则化常数使用前面实验得到的最优参数。初始化后,采用共轭梯度算法精调整个网络(与文献[20]相同),但是迭代步数为50(文献[20]中为200),图9和图10分别为各模型针对不同训练样本数和测试样本数的误差图,图11为各深度模型的迭代误差图。最后使用MNIST数据集的测试结果对精调后的网络进行分类率的测试,最终得到的结果如表8所示。

图9 各模型训练误差曲线图
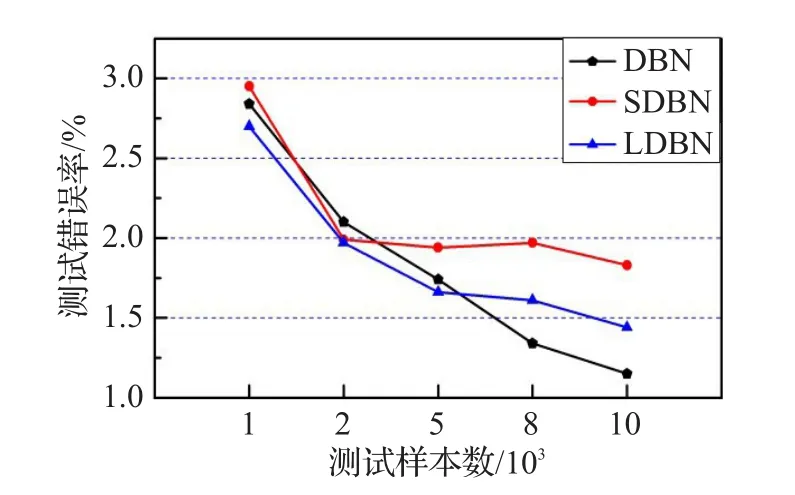
图10 各模型测试误差曲线图

表8 基于RBM、SRBM、LRBM的深度置信网对MNIST数据集的分类率 %
从表8可以看出,经过50步共轭梯度算法精调后的DBN网络的分类率为98.85%,这与文献[20]得到的98.87%非常接近,而SDBN网络得到的分类率为98.17%与文献[10]报告的98.20%同样非常接近;虽然SDBN和LDBN得到的分类率较略低于DBN的分类率,但是三者非常接近,差别非常小。说明使用SRBM或LRBM堆叠而成的深度模型同样实现对数据的高度正确分类。
从图9不难看出,随着训练样本数的增加,所得的分类错误率大大降低。在训练样本数较少时,SDBN和LDBN展示出较好的分类性能,可以有效地解决样本数较少造成的分类精度较低的问题。
图10是在训练样本数均为60 000时得到的分类错误率。随着测试样本数的增加,测试错误率也有所降低,每个模型最大与最小的误差率之间最大差值在2%左右,可见在训练阶段结束以后,各模型分类能力基本稳定。增加测试样本数量并未造成太大的影响。
各深度模型的最终分类率的差异可以忽略不计,但是各深度模型的组成单元对模型精调阶段的影响是不同的。虽然迭代50步所得的结果与迭代200步所得的结果极其接近,但是从图11可以看出DBN网络中使用共轭梯度法迭代50步仍未收敛到固定值上,而SDBN和LDBN则分别只用了37步和30步就收敛到一个固定值上。不但说明了经过稀疏约束后的RBM堆叠而成的深度模型,可以维持分类率基本不变的情况下大幅度加快模型得到最终分类率的速度,而且说明了使用由Lorentz函数作为稀疏约束项的LRBM堆叠而成的深度模型得到最终分类率的速度要快于由SRBM堆叠而成的深度模型。

图11 各模型的迭代误差曲线图
5.2 基于CIFAR-10数据集实验分析
CIFAR-10数据集[21]是由加拿大的一个先进科学项目研究所——加拿大高等研究院(Canadian Institute for Advanced Research,CIFAR)收集的用于普适物体识别的数据集。CIFAR-10数据集是由动物和车辆的图片组成,包含飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船和卡车等10类。每一类由6 000张32×32的彩色图片构成,其中5 000张被保存在训练集中,1 000张在测试集中。图12给出了CIFAR-10数据集的部分样本。

图12 CIFAR-10数据集的部分样本
与MNIST数据集类似,从该数据集中随机选取每类2 000个训练样本作为LRBM以及对比模型的训练样本,并将其分成200组各包括100个样本的小批量数据。
本节将训练模型RBM、SRBM、LRBM,其隐单元均设置为1 000。与前面的实验类似,选取各模型分类率最高的参数进行实验,将LRBM以及其他一些无监督学习模型的输出作为线性分类器的输入,以重复训练20次线性分类器所得的平均分类率评价各无监督学习算法对CIFAR-10数据集的可判别性能。不同的是,这里仅将每类的1 000个样本作为线性分类器的训练样本。表9为各模型间分类精度之间的对比。

表9 各模型的平均分类率 %
如表9所示,在相同样本数的情况下,LRBM分类率均明显优于其他无监督学习模型,较RBM明显提高了约5个百分点。
为进一步比较各模型的特征提取性能,展示模型学习到的特征的好坏。因此,对RBM、SRBM、LRBM横型第一层所学习到的部分特征进行可视化,如图13所示。

图13 各模型学习到的部分特征
图13为对RBM、SRBM、LRBM模型第一层学习到的部分特征进行可视化的结果,不难看出RBM和SRBM学习到的特征类似,用肉眼很难判断各自的好坏,而LRBM学习到的特征中,杂乱无序的特征较其他模型要少一些。
由于目前对深度结构网络各层学习到的特征进行可视化非常困难,当训练集为彩色图像时更难以可视化。因此,将各模型针对CIFAR-10数据集所学习到的特征的可视化效果并不理想,关于深度结构各层特征可视化问题还有待进一步深入的研究。
造成对CIFAR-10数据集分类率远远低于MNIST数据集分类率的原因,主要是相对于MNIST数据集,CIFAR-10数据集每类目标训练样本为明显增加而复杂度却大幅增加。同时,由于无监督算法需要大量的样本进行训练,虽然LRBM在一定程度上改善了这个问题,但是对于样本复杂度远高于MNIST数据集的CIFAR-10数据集,各个无监督学习算法(包括LRBM)的性能会有大幅度下降,可以通过大量增加训练样本数量的方法,来改进上述问题。
6 结束语
在DBN网络中,RBM扮演着特征提取器的角色,因此对RBM的学习算法进行进一步改进,使得其特征提取能力进一步提高。针对这一问题,本文提出了一种稀疏RBM算法,将Lorentz函数引入到RBM中,并作为RBM的稀疏约束正则项,以提高其特征提取性能,实验证明了该算法的有效性。其有效性主要表现在两个方面:
(1)增加了稀疏约束正则项后,提高了数据集的平均分类率,加强了深度网络可视化表示程度,实现了目标分类的可靠性。
(2)由LRBM堆叠组成的稀疏DBN,进一步加强了目标学习的准确性,能够有效地提取数据集中的特征信息,同时提高了目标分类的效率。
对于LRBM模型和深度网络的理论和算法,可得出作为特征提取器具有较优的性能。从理论上讲,LRBM是可以用于提取高分辨率遥感影像中的特征,可以作为后续的研究之一。
参考文献:
[1]Hepner G F,Logan T,Ritter N,et al.Artificial neural network classification using a minimal training set:Comparisontoconventionalsupervisedclassification[J].Photogrammetric Engineering&Remote Sensing,1990,56(14):207-222.
[2]Tzeng Y C,Chen K S,Kao W L,et al.A dynamic learning neural network for remote sensing applications[J].IEEE Transactions on Geoscience&Remote Sensing,1994,32(5):1096-1102.
[3]Serpico S B,Burzzone L,Roli F.An experimental comparison of neural and statistical non-parametric algorithm for supervised classification of remote-sensing images[J].Pattern Recognition Letters,1996,17(13):1331-1341.
[4]Murnion S D.Comparison of back propagation and binary diamondneuralnetworksintheclassificationofa Landsat TM image[J].Computers&Geosciences,1996,22(9):995-1001.
[5]Hinton G E,Sejnowski T J.Learning and relearning in Boltzmann machines[M]//Parallel Distributed Processing:ExplorationsintheMicrostructureofCognition.Cambridge,MA,USA:MIT Press,1986:282-317.
[6]Smolensky P.Information processing in dynamical systems:Foundation of harmony theory,CU-CS-321-86[R].1986.
[7]Hinton G E.Training products of experts by minimizing contrastive divergence[J].Neural Computation,2002,14(8):1771-1800.
[8]Fischer A,Lgel C.Training restricted Boltzmann machines:An introduction[J].Pattern Recognition,2014,47(1):25-39.
[9]Hinton G E,Dayan P,Freyb B J,et al.The“wake-sleep”algorithm for unsupervised neural networks[J].Science,1995,268:1158-1161.
[10]Lee H,Ekanadham C,Ng A.Sparse deep belief net model for visual area V2[C]//Proc of Advances in Neural Information Processing Systems,2007:1416-1423.
[11]Luo H,Shen R,Niu C,et al.Sparse group restricted Boltzmann machines[C]//Proc of the 25th AAAI Conference on Artificial Intelligence,2011:429-434.
[12]Ji N N,Zhang J S,Zhang C X.A sparse-response deep belief network based on rate distortion theory[J].Pattern Recognition,2014,47(1):3179-3191.
[13]Zhou Guoquan,Wang Xiaogang,Chu Xiuxiang.Fractional Fourier transform of Lorentz-Gauss vortex beams[J].Science China,Physics,Mechanics&Astronomy,2013,56(8):1487-1494.
[14]王光新.基于稀疏约束正则化模型的图像提高分辨率技术研究[D].长沙:国防科学技术大学,2008.
[15]Freund Y,Haussler D.Unsupervised learning of distributions on binary vectors using two layer networks[C]//Proceedings of Advances in Neural Information Processing Systems,1992:912-919.
[16]Fischer A,Lgel C.An introduction to restricted Boltzmann machines[C]//Progress in Pattern Recognition,Image Analysis,Computer Vision,and Applications,2012:14-36.
[17]Bengio Y.Learning deep architectures for AI[J].Foundations and Trends in Machine Learning,2009,2(1):1-127.
[18]Sacchi M D,Ulrych T J,Walker C J.Interpolation and extrapolation using a high-resolution discrete Fourier transform[J].IEEE Transactions on Signal Processing,1998,46(1):31-38.
[19]Hoyer P O.Non-negative matrix factorization with sparseness constraints[J].The Journal of Machine Learning Research,2004,5:1457-1469.
[20]Hinton G E,Osindero S,Teh Y.A fast learning algorithm for deep belief nets[J].Neural Computation,2006,18(7):1527-1554.
[21]Krizhevsky A,Hinton G E.Learning multiple layers of features from tiny images[J].Handbook of Systemic Autoimmune Diseases,2009,1(4).

