超高层建筑结构抗风性能研究

李　宇，付　曜，李　琛

(1. 长安大学公路学院，陕西西安　710064； 2. 长安大学建筑学院，陕西西安　710061)

0　引　言

风荷载是超高层建筑结构的主要水平向荷载，特别是对于位于台风多发地区的超高层建筑，其风致振动则成为结构设计要考虑的首要因素。随着许多超高层建筑在全国各地的兴建，其抗风性能问题已成为研究热点[1]。Davenport[2-3]在研究高层建筑等效静力风荷载时提出阵风荷载因子法；Simiu[4-5]提出了计算超高层建筑等效静力风荷载的新方法；Solari[6-7]对超高层建筑结构横风向的风致振动及其计算方法进行了研究；Kasperski等[8-9]针对线性和非线性超高层建筑提出了计算最大分布风荷载的方法；Marukawa等[10]对棱柱形超高层建筑横风向和扭转向的加速度响应进行了研究；全涌等[11-17]对超高层建筑进行了气动弹性模型风洞试验研究，探讨了风致振动和等效静力风荷载的计算方法。

目前，中国现行的《建筑结构荷载规范》(GB 50009—2012)[18]采用风振系数来表征高层建筑顺风向的动力风效应，其计算公式仅适用于规则结构，且仅考虑结构基阶振型。超高层建筑往往具有体型复杂、周围建筑密集、气动力干扰明显等特征，按规范公式计算得到的超高层建筑动力风效应不尽合理。因此，本文在上述学者的研究基础上,将风洞试验与有限元计算分析相结合，以此来计算超高层建筑的风致振动响应(风振系数、结构脉动风时程响应、等效静风荷载等)，进而研究超高层建筑的抗风性能。

1　风洞试验测得各楼层的风荷载

本文首先进行了某超高层建筑的风洞试验以测得结构的风压系数[19]，进而计算出有限元分析所需的各楼层风荷载，为超高层建筑抗风性能研究提供必要数据。

1.1　工程概况

图1为某超高层建筑效果图，包含1#楼(主楼)和2#楼(配楼)，由于所处位置海拔较高，且1#楼(主楼)高达299.3 m，风荷载是其主要荷载之一。为了确保其的抗风安全性，对其进行风洞试验是必要的。

图1　西安环球贸易中心超高层建筑Fig.1　Super High-rise Building of Xi’an Global Trade Center

1.2　试验方法

图2　风洞试验Fig.2　Wind Tunnel Test

风洞试验在长安大学风洞实验室CA-1大气边界层风洞中进行。试验模型为一刚体模型(图2)，具有足够的强度和刚度，在10 m·s-1的试验风速下不发生破坏并且不出现振动，保证了测量的精度，模型的几何缩尺比为1∶280。模型的方位、风向角约定以及坐标轴与风向角的关系如图3所示，即X轴指向90°风向，Y轴指向180°风向，Z轴为竖直向。采样频率、采样时间、样本长度及时间相似比如表1所示。

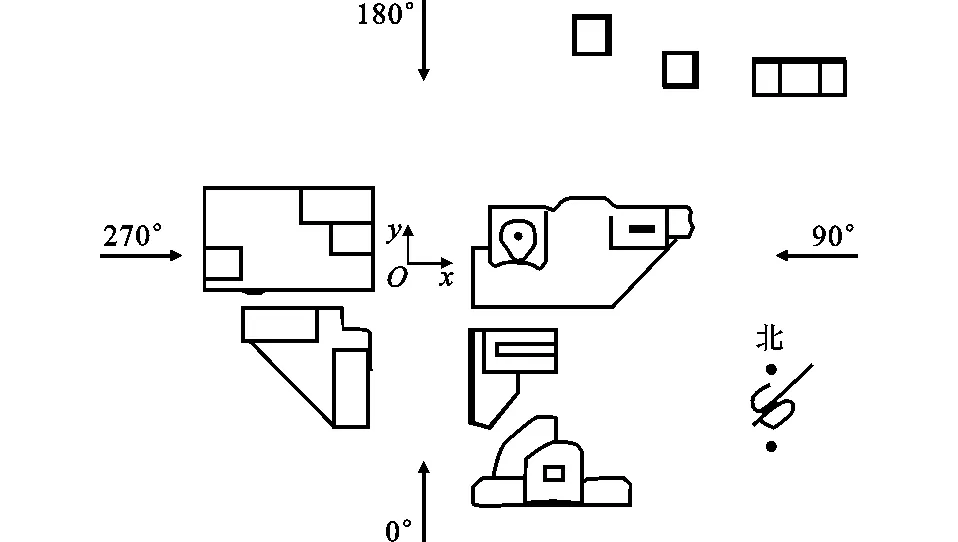
图3　坐标轴和风向角Fig.3　Coordinate Axis and Wind Angle

试验工况为：①全封闭试验，取用D类地貌风场；②风向角为0°～350°，每隔10°设置1个测点，共36个；③1#楼模型共分14个区域进行测压，其中模型楼底第1区高度为60.5 mm，第2～13区每区高度为80.4 mm，第14区高度为43.6 mm，第14区西侧、北侧及西北侧为双面测压，其余为单面测压，共设测点328个；④2#楼模型共分9个区域进行测压，自模型底90 mm起每区高度为60 mm，其中第9区为双面测压，其余为单面测压，共设测点140个。

表1　试验主要参数Tab.1　Main Test Parameters

1.3 各楼层风荷载的计算

通过风洞试验可得到不同风向角下结构各测点的脉动风压系数，再通过积分方法可得到结构每一楼层上的分力。设作用在结构某层上沿X方向、Y方向的总水平风荷载和绕Z轴的总扭转风荷载时程分别为FXm(tm)，FYm(tm)，MZm(tm)，则可以得到各层量纲一的风力系数时程μFX(tm)，μFY(tm)，μMZ(tm)[11-12]，即

(1)

式中：Um为与结构某层同高度的试验风速；ρ为空气密度；tm为模型系统的时间；Hm为结构层高；DXm，DYm分别为X向、Y向的特征尺寸。

根据时间相似比λt可得原型的时间序列tk,p为

tk,p=tk,m/λt

(2)

式中：tk,m为第k个采样时刻的模型时间序列，p代表原型。

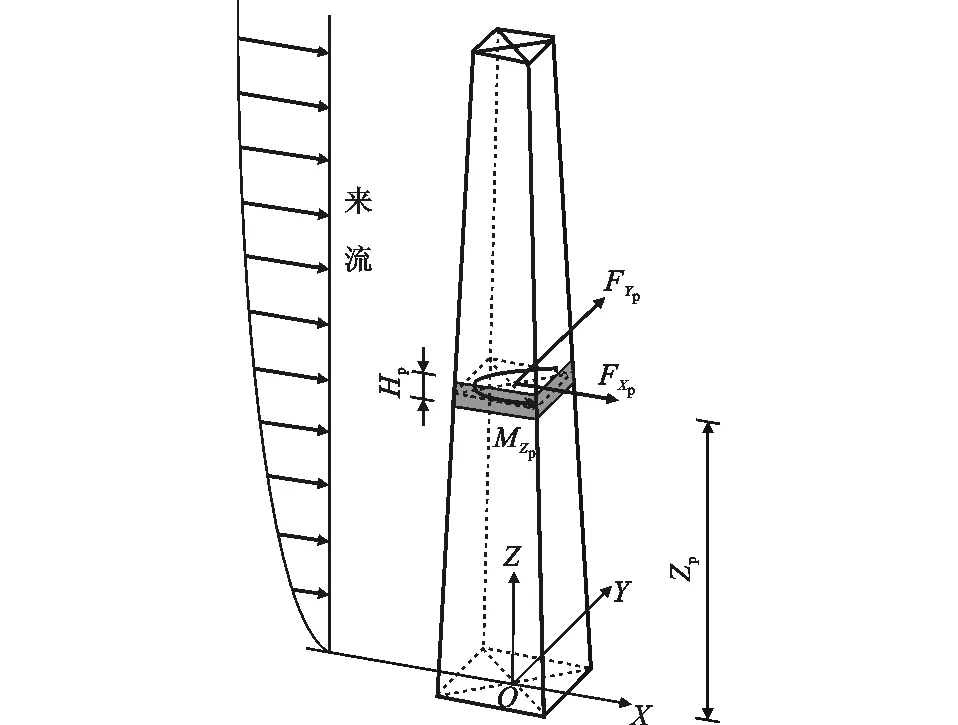
图4　作用在结构上的风荷载Fig.4　Wind Load Applied on Structure

这样把式(1)中的模型系统时间改为实际时间，即可得结构原型的风力系数时程μFX(tm)，μFY(tm)和μMZ(tm)，进而可确定作用在结构原型上的风荷载(图4)。设FXp(tp)，FYp(tp)和MZp(tp)分别为作用在结构原型某层(离地高度为Z，层高为Hp)质心处沿正交轴X，Y方向的水平风荷载和绕Z轴的扭转风荷载时程(图5)，则[14-15]

(3)

图5　顶层风荷载时程(0°风向角)Fig.5　Wind Load Time-history Curve of Top Floor (0° Wind Angle)

式中：μFX(tp)，μFY(tp)，μMZ(tp)应根据某层的具体大小取值；DXp，DYp为结构原型截面特征尺寸；UZ为实际边界层风场中高度Z处的风速。

限于篇幅以下仅给出顶层(第64层，0°风向角)的风荷载时程，其他数据参考文献[19]。在得到上述结果后，即可将风荷载输入至有限元模型，进而采用ANSYS进行超高层建筑的抗风性能研究。

2　有限元模型的建立

超高层建筑具有结构高、柔性大、小阻尼、自振频率低等特点，属于风敏感性结构，在自然风的作用下易发生共振而受损。本文采用“串联多质点系”力学模型来建立1#楼的有限元模型(图6，其中M1，Mi，Mt，Mn分别为第1，i，t，n层楼的质量)每层质点考虑2个方向的平动质量和剪切刚度、绕竖向参考轴的转动惯量和扭转刚度。竖向参考轴取结构每层的质心轴。风荷载考虑2个平动方向的水平力及绕竖向参考轴的扭矩。

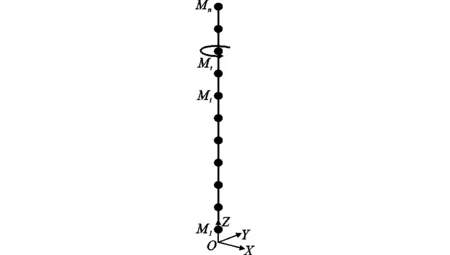
图6　串联多质点系模型Fig.6　Series-wound More Particle Model

3　风振系数的计算

《建筑结构荷载规范》(GB 50009—2012)[18]中结构的风振系数定义为“总风荷载的概率统计值与静风荷载的概率统计值的比值”，其中，总风荷载包括平均风荷载和脉动风荷载两部分。由于该荷载风振系数主要针对以第一振动模态为主的结构提出，对于自振频率分布密集的超高层建筑结构，结构的不同位置、不同构件之间的风振系数存在较大的离散性，因此很难用统一的风振系数来表述整个结构的风振响应特征。通常动荷载可以转化为静荷载与动力效应系数的乘积，其动力效应系数的表示方法有位移风振系数和内力风振系数。已有研究表明[1-19]：位移和内力风振系数沿超高层建筑的表面分布比较均匀，采用它们取代规范中的荷载风振系数后，计算所得的内力基本一致，依然可按照荷载规范所采用公式进行结构风荷载计算。

本文将第1节计算出的1～64层总风荷载时程向量加载到“串联多质点系”有限元模型中的64个楼层所对应的节点进行动力时程响应分析，计算脉动风和平均风所产生的位移和内力响应，并根据式(4)计算1～64层迎风向和横风向的风振系数βZ

βZ=(Rs+Rd)/Rs=1+Rd/Rs=1+gσR/Rs

(4)

式中：Rs为平均风所产生的结构位移或内力响应；Rd为脉动风所产生的结构位移或内力响应极值；g为峰值因子；σR为结构某个响应R(可以是位移、加速度或内力等)的根方差。

在此基础上，本文计算了不同风向角下1#楼“串联多质点系”的64个楼层迎风向和横风向的风振系数(图7)。从图7可知：①当风荷载与超高层建筑的迎风面夹角φ接近90°时，其水平向的最大和最小位移风振系数都发生在结构的中部；②当风荷载与超高层建筑的迎风面夹角在20°～70°之间时，位移风振系数则随着楼层的增高而增加，其峰值则出现在顶层。

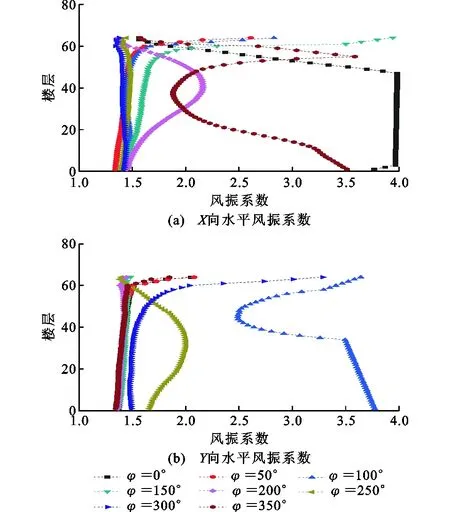
图7　不同风向角下的风振系数Fig.7　Wind Vibration Coefficients with Different Wind Angles

4　结构的舒适度验算

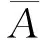
(5)

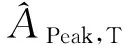
(6)

图8给出了1#楼顶层的加速度峰值随风向角变化的曲线(10年重现期，结构阻尼比为0.01)。从图8可见：

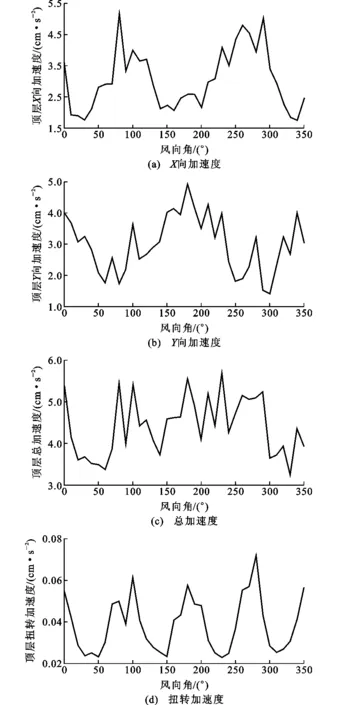
图8　加速度峰值随风向角的变化Fig.8　Variations of Peak Acceleration with Wind Angle

(1)结构X向加速度峰值发生在80°风向角，为0.051 7 m·s-2；Y向加速度峰值发生在180°风向角，为0.049 2 m·s-2；最大总加速度峰值发生在230°风向角，为0.057 m·s-2。可见，上述各加速度峰值都小于高层结构顶部最大加速度限值0.25 m·s-2[11-15]，即此高层建筑结构满足结构舒适度的要求。

(2)超高层建筑的顶层水平加速度峰值一般发生在风荷载与迎风面相垂直的时候，而且其扭转加速度峰值的变化趋势在每个区间(0°～90°，90°～180°，180°～270°，270°～350°)都是先减小后增大。

5　结构的刚度验算

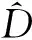
(7)

(8)

图9给出了1#楼顶层位移峰值随风向角变化的曲线(50年重现期，结构阻尼比为0.02)。从图9可见：

图9　位移峰值随风向角的变化Fig.9　Variations of Peak Displacement with Wind Angle

(1)X向位移峰值发生在250°～270°风向角，为10.3 cm；Y向位移峰值发生在210°，为9.95 cm；总位移峰值发生在230°风向角，为12.3 cm。上述位移峰值皆小于结构总高度的0.1%(29.93 cm)，即满足结构刚度验算的要求[11-15]。

(2)超高层建筑的顶层位移峰值也是发生在风荷载与迎风面相垂直的时候，此时迎风面的顺风向位移达到最大值，而其横风向位移则相应地最小。这是因为超高层建筑的前2阶主要振型都是以水平向运动为主。

(3)当风荷载与迎风面呈45°左右的夹角时，超高层建筑的扭转变形达到最大值，这与超高层建筑的第3阶振型以扭转变形为主密切相关。

6　结构的强度验算

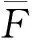
(9)

(10)

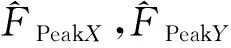
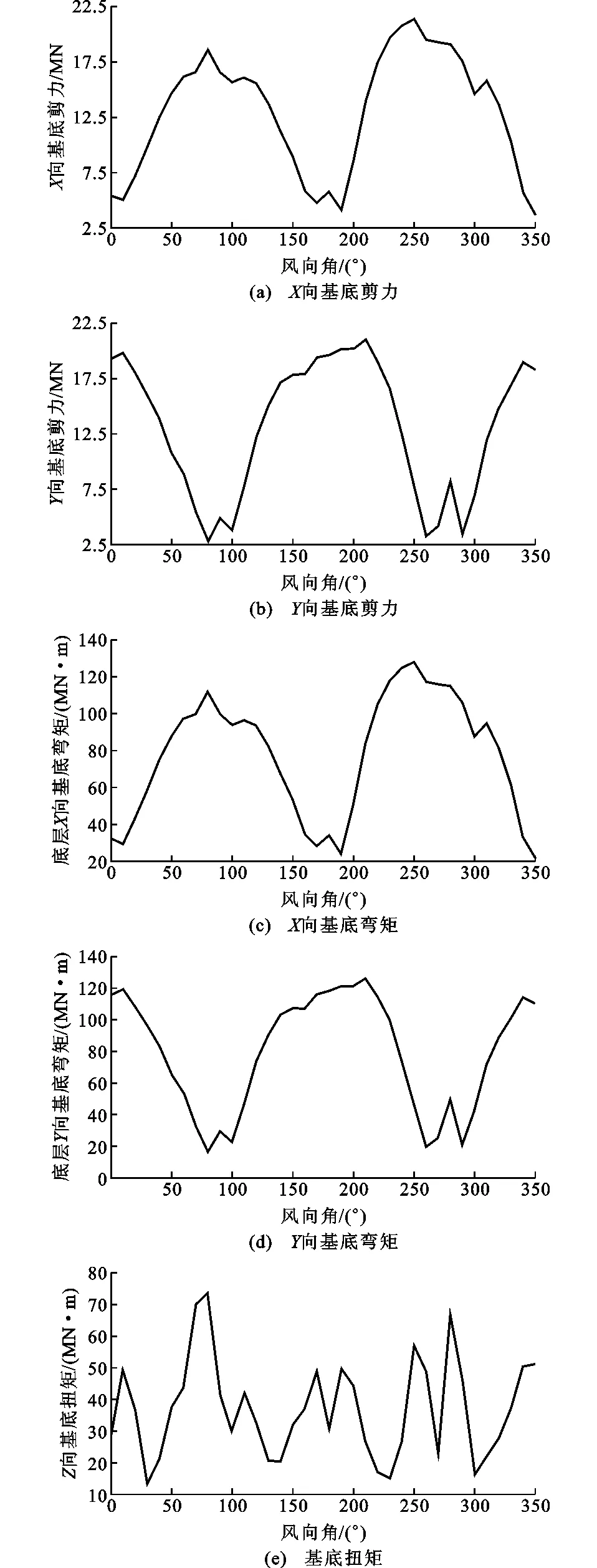
图10　内力峰值随风向角的变化Fig.10　Variations of Peak Internal Force with Wind Angle

图10给出了1#楼基底峰值剪力、峰值扭矩和倾覆力矩随风向角变化的曲线(100年重现期，结构阻尼比为0.04)。从图10可见：

(1)X轴向峰值剪力发生在250°风向角，为21 400 kN；Y轴向峰值剪力发生在210°风向角，为21 000 kN；绕X轴峰值倾覆力矩发生在250°风向角，为128 000 kN·m；绕Y轴峰值倾覆力矩发生在210°风向角，为126 000 kN·m；绕Z轴峰值扭矩发生在80°风向角，为73 600 kN·m。上述内力峰值皆小于规范要求[11-15]，即满足结构强度验算。

(2)超高层建筑的基底内力与风向相关：当风荷载与迎风面相垂直时，迎风面的基底剪力与弯矩达到最大值，而其横风向的基底剪力与弯矩则相应地最小。基底扭矩的峰值发生在风荷载与迎风面的夹角为45°时。

7　等效静力风荷载

如果能用一组静力荷载施加在结构上，使其产生的响应正好与按照随机振动理论计算得到的结构各处极值位移或者内力响应基本相符，那么就可将这组静力荷载作为等效静力风荷载，这是联系结构抗风研究和结构抗风设计的桥梁。根据《建筑结构荷载规范》(GB 50009—2012)[18]第8.1.1条，垂直于建筑物表面上的风荷载标准值应按下式确定

Wk=βZμsμzωo

(11)

式中：Wk为风荷载标准值；μs为风荷载体型系数；μz为风压高度变化系数；ωo为基本风压，10，50，100年一遇的基本风压分别为0.20，0.35，0.40 kPa。

根据公式(11)，本文在考虑了周边建筑的气动干扰效应以及横风向风振等问题的基础上，计算了对应于不同风向角(0°～350°)下“串联多质点系”力学模型1#楼的各层等效静风风压，并乘以相应的几何参数，进而给出以质心为作用点，按内力响应峰值等效的等效静力风荷载FX，FY，MZ(对应于图4所示的模型坐标系)。

图11给出了1#楼的等效静力风荷载随风向角变化的曲线(50年重现期，结构阻尼比为0.04)。从图11可见：各楼层的等效静力风荷载与风向角的变化密切相关，水平等效静力风荷载随着楼层的增加其变化规律较为一致，而扭转等效静力风荷载的变化规律则比较复杂。

图11　不同风向角下的等效静力风荷载Fig.11　Equivalent Aerostatic Force Loads with Different Wind Angles

8　结语

(1)当风荷载与超高层建筑的迎风面夹角接近90°时，其水平向的位移风振系数极值发生在结构中部；当夹角在20°～70°之间时，位移风振系数随着楼层的增高而增加，其峰值出现在顶层。

(2)超高层建筑的顶层水平加速度峰值、顶层水平位移峰值和基底剪力与弯矩都是发生在风荷载与迎风面相垂直的时候，此时迎风面顺风向的变形和内力都达到了最大值，而其横风向的变形和内力则最小。

(3)随着风向角的变化，超高层建筑的扭转加速度峰值在每个区间(0°～90°，90°～180°，180°～270°，270°～350°)都是先减小后增大。特别是当风荷载与迎风面呈45°左右夹角的时候，超高层建筑的扭转变形和基底扭矩达到了最大值，这与超高层建筑的第3阶振型以扭转变形为主密切相关。

参考文献：

[1]克拉夫R W,彭津J.结构动力学[M].王光远,译.北京:科学出版社,1981.

CLOUGH R W,PENZIEN J.Dynamics of Structure[M].Translated by WANG Guang-yuan.Beijing:Science Press,1981.

[2]DAVENPORT A G.Gust Loading Factors[J].Journal of the Structural Division,1967,93(3):11-34.

[3]DAVENPORT A G.The Response of Slender,Link-like Structures to a Gust Wind[J].Proceedings of the Institution of Civil Engineers,1962,23(3):389-408.

[4]SIMIU E.Equivalent Static Wind Loads for Tall Buildings Design[J].Journal of the Structural Division,1976,102(4):719-737.

[5]SIMIU E.Revised Procedure for Estimating Alongwind Response[J].Journal of the Structural Division,1980,106(1):1-10.

[6]SOLARI G.Alongwind Response Estimation:Closed Form Solution[J].Journal of the Structural,Division,1982,108(1):225-244.

[7]SOLARI G.Analytical Estimation of the Alongwind Response of Structures[J].Journal of Wind Engineering and Industrial Aerodynamics,1983,14(1/2/3):467-477.

[8]KASPERSKI M.Extreme Wind Load Distributions for Linear and Nonlinear Design[J].Engineering Structures,1992,14(1):27-34.

[9]KASPERSKI M,NIEMANN H J.The L.R.C.(Load-response-correlation)-method:A General Met-hod of Estimating Unfavorable Wind Load Distributions for Linear and Non-linear Structural Behaviour[J].Journal of Wind Engineering and Industrial Aerodynamics,1992,41(1/2/3):1753-1763.

[10]MARUKAWA H,OHKUMA T,MOMOMURA Y.Across-wind and Torsional Acceleration of Prismatic High Rise Buildings[J].Journal of Wind Engineering and Industrial Aerodynamics,1992,42(1/2/3):1139-1150.

[11]全涌.超高层建筑气动弹性模型的风洞试验研究[D].上海:同济大学,1999.

QUAN Yong.Experimental of Aerodynamic Elasticity of Super-high Rise Buildings in Wind Tunnel[D].Shanghai:Tongii University,1999.

[12]全涌.超高层建筑横风向风荷载及响应研究[D].上海:同济大学,2002.

QUAN Yong.Super High Rise BuiIdings’ Wind Loads and Response in Across Wind Direction[D].Shanghai:Tongii University,2002.

[13]周印.高层建筑静力等效风荷载和响应的理论与实验研究[D].上海:同济大学,1998.

ZHOU Yin.Theoretical and Experimental Investigations on Effective Static Wind Loads on High Rise Buildings[D].Shanghai:Tongii University,1998.

[14]全涌,顾明.超高层建筑横风向气动力谱[J].同济大学学报,2002,30(5):627-632.

QUAN Yong,GU Ming.Power Spectra of Across-wind Loads on Super High-rise Buildings[J].Journal of Tongji University,2002,30(5):627-632.

[15]全涌,顾明.方形断面高层建筑的气动阻尼的风洞试验研究[J].工程力学,2004,21(1):26-30.

QUAN Yong,GU Ming.Wind Tunnel Test Study of Aerodynamic Damping of Super High-rise Buildings[J].Engineering Mechanics,2004,21(1):26-30.

[16]叶丰.高层建筑顺、横风向和扭转方向风致响应及静力等效风荷载研究[D].上海:同济大学,2004.

YE Feng.Study on Along-wind,Across-wind and Torsion Response and Equivalent Static Wind Loads of High-rise Buildings[D].Shanghai:Tongji University,2004.

[17]叶丰.高层建筑顺风向风荷载及其响应研究[D].上海:同济大学,2000.

YE Feng.Study on Along-wind Loads and Responses of High-rise Buildings[D].Shanghai:Tongji University,2000.

[18]GB 50009—2012,建筑结构荷载规范[S].

GB 50009—2012,Load Code for the Design of Building Structures[S].

[19]长安大学风洞实验室.西安环球贸易中心一号楼及二号楼风洞试验[R].西安:长安大学风洞试验室,2014.

Wind Tunnel Laboratory of Chang’an University.Wind Tunnel Test for No.1 and No.2 Building of Xi’an World Trade Center[R].Xi’an:Wind Tunnel Laboratory of Chang’an University,2014.