基于NSCT的乳腺图像分类方法*
胡良田,潘海为,谢晓芹,张志强,冯晓宁
哈尔滨工程大学 计算机科学与技术学院,哈尔滨 150001
1 引言
当今,乳腺癌已成为女性发病率最高的癌症之一。据世界卫生组织报告,在2008年至2012年期间乳腺癌的发病率以及死亡率分别增加了约20%和14%[1]。面对日益严峻的健康形势,技术工作者们提出了一种从自我检测活动到基于医学图像的乳腺癌早期检测技术,特别是对乳腺X线图像的研究,使得乳腺癌的死亡率得到了一定的控制。但是,通过X线摄影所获得的乳腺图像有些会不可避免地包含一些噪音,如与病变区灰度级极其接近的脂肪型乳腺组织,对于这种情况即使有经验的放射科医师都难以准确鉴别出肿瘤的类型(良性、恶性、正常)[2-3],且在密集的乳腺病例中,有这种类型的乳腺患者通常是年轻患者。可见,针对脂肪型乳腺癌肿瘤分类的研究具有很强的实际应用价值和社会价值。
目前,基于乳腺X线图像的分类方法有:(1)Wang等人(2014)提出了基于区域生长检测病变的方法[4];(2)Saki等人(2011)将泽尼克矩(Z-Moments)用作形状描述符的方法[5];(3)Saki等人(2013)采用了突出指数来表示病变边界的几何形状的方法[6];(4)Rouhi等人(2015)在特征提取阶段采用卷积神经网络(convolutional neural network,CNN)分割的策略[7];(5)Sidney等人(2016)提出的通过小波变换法检测和分类乳腺X线图像的方法。
但因为乳腺X线图像并不能很完美地呈现出肿瘤的轮廓,所以以上所提的前4种对肿瘤进行分类的方法都需要医生手动地给出每张图片的肿瘤区域。Sidney等人提出的第5种方法并不需要人工提取肿瘤轮廓,而是通过小波变换将原始乳腺图像分解成一系列不同空间分辨率和频率特性的子图像,反映了原始乳腺图像的局部变化特征。从而可以使用ZMoments从不同的子图像中提取各种特征信息。但小波变换只具有水平、垂直、对角线3个方向细节信息,并且采用下采样的方式对原始乳腺图像进行分解,因此其对原始乳腺图像的边缘及线状特征等线、面的奇异性难以很好地表达[8]。
分类方法作为影响实验效果的重要因素,并不是没有差异的,选择好的分类方法对乳腺图像进行正确的分类是实验成功的关键。Sidney等人对其所获得的实验数据采用不同的分类方法进行实验,并对结果进行比较。发现支持向量机(support vector machines,SVM)的linear核函数具有最好的分类效果。但是Sidney等人没有对其数据进行任何清洗工作,导致数据量大且杂,因此选择好的数据清洗方法也很重要。
针对上述存在的问题,本文提出一种基于非下采样轮廓变换法(nonsubsampled contourlet transform,NSCT)的乳腺X线图像分类方法。对预处理后的脂肪型乳腺X线图像进行NSCT图像分解,得到原始乳腺图像的一系列子图像,然后通过Z-Moments从子图像中提取特征获得大量数据,对这些数据通过奇异值分解(singular value decomposition,SVD)的方法进行清洗处理后再运用不同分类方法对其分类。这样不仅减小了数据量,提升了数据质量,使得分类的准确率和时间效率都优于Sidney等人提出的方法。
本文组织结构如下:第2章为乳腺X线图像的预处理过程;第3章主要介绍本文方法的框架;第4章分为三大部分,第一部分介绍非下采样轮廓变换法(NSCT)的原理及其应用,第二部分提出了Z-Moments的构建过程,第三部分讨论了SVM的分类算法;第5章介绍实验的数据集并展示实验结果;第6章总结本文并展望未来工作。
2 预处理过程
下面主要研究对乳腺X线图像采用数学形态学方法进行预处理的过程。
数学形态学在图像处理中属于非线性滤波方法,且已经发展成为图像处理技术的重要方面。数学形态学有4个基本运算:膨胀(或扩张)、腐蚀(或侵蚀)、开启和闭合,它们在二值图像和灰度图像中各有特点[9-12]。基于这些方法可以组合出很多数学形态学的实用算法,用它可以对图像的形状和结构进行分析处理,包括图像分割、特征抽取、边界检测、图像滤波、图像增强和恢复等。
下面的等式(1)和等式(2)分别是腐蚀和膨胀在数学上的表达式:

其中f:S→[0,1]和g:S→[0,1]是标准化单光谱图像,且S⊆Z2,符号⋃和∨与最大运算操作相关联,符号⋂和∧与最小运算操作相关联,且对∀u∈S,g:S→[0,1]是相应的侵蚀和扩张的结构元素[9-12]。
结合侵蚀和膨胀的数学表达式,可以得到开启的数学表达式γg(f)(u),其运用了先侵蚀后膨胀的原理。其次考虑标准化单光谱图像f:S→[0,1]由结构元素g:S→[0,1]第k次开启操作产生的剩余区域(k≥0)的数学表达式为:

通过以上对数学形态学基本运算的描述,可以得到表达式(4),离散累积密度函数:

离散密度函数,也称为模式谱或形态光谱,它的核心由等式(5)描述[12]。通过形态学理论了解到其保证每个二进制图像具有基于该光谱的独特表示,因此图案或形态光谱可以作为基于形状的非常精确的特征提取器使用。并且模式光谱具有可以忽略乳腺质量边缘的不规则性导致形态光谱的低振幅变化的能力,及其可以在不管肿瘤大小的情况下用作肿瘤形状的独特表示。这些就是形态光谱成为本文对乳腺X线图像进行预处理方法的原因。

为了计算图像的形态光谱,必须执行等式(5)的操作直到算法收敛。数据库中不同的乳腺X线图像需要不同次数的迭代计算得到其形态光谱结果,因此为了避免形态光谱大小不同的问题,将使用7个统计量来表示这些光谱,即平均值、标准差、模式、中值、峰度、最小值和最大值。
3 框架介绍
以下介绍预处理后乳腺X线图像的特征提取和分类框架。
通过乳腺X线图像分类乳腺病变的方法高度依赖于特征提取阶段。本文采用NSCT和Z-Moments的特征提取法,其整体框架如图1所示。使用通过专业临床知识确定的感兴趣区域,对图像进行预处理。多分辨率NSCT和Z-Moments相结合可以混合纹理和形状特征,改善分类阶段的图像表示。
对预处理后的图像进行特征提取的第一阶段NSCT:感兴趣区域作为非下采样塔式滤波器组(nonsubsampled pyramid filter bank,NSPFB)的输入图像,将被分解为低通子带图像(lowpasssubbandimage,LSI)和带通子带图像(bandpass subband image,BSI),以实现图像的多尺度分解;然后利用非下采样方向滤波器组(nonsubsampled directional filter bank,NSDFB)将BSI分解为多个方向子带图像即带通方向子带图像(bandpass directional subband image,BDSI),以实现图像的多方向分解;最后对每一层的LSI重复上述操作,得到输入图像的多层NSCT[13]。一张原始乳腺X线图像经过第一尺度的NSPFB分解得到图像LSI1和BSI2。随后经过第二尺度的NSPFB分解得到图像LSI2和BSI2,以此类推。
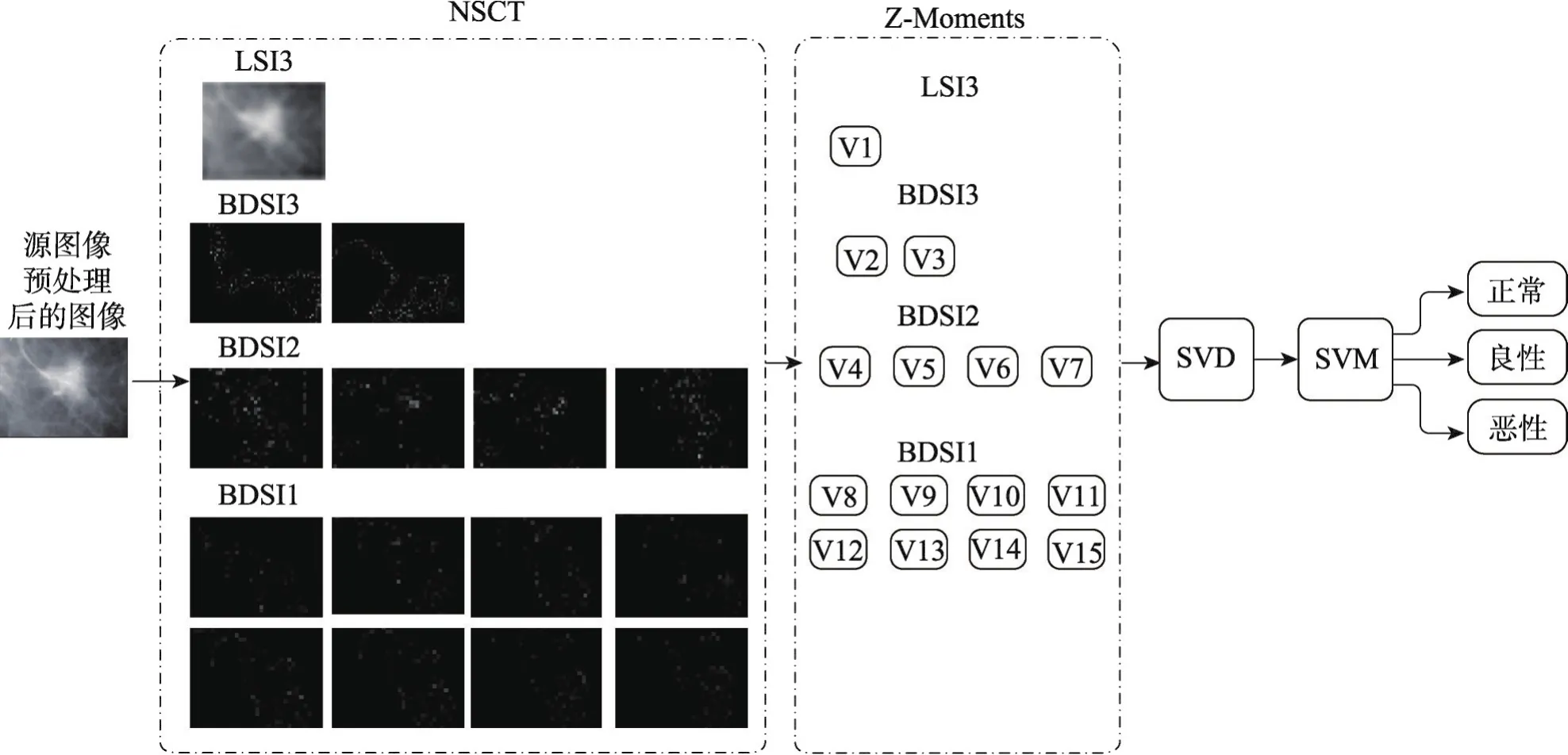
Fig.1 Overall frame图1 整体框架
若对BSIn(n∈1,2,…,n)经过m级方向分解,即可得到2m个与原始图像相同大小的m级的BDSI,称为BDSIm。原始X线图像经过J层NSCT分解后可得到1个LSIJ以及个BDSI,其中mj为尺度j下的方向级数。
根据以上的描述,在此可以定义几个概念:
定义1(低通子带图像LSI)

其中LSIi表示第i尺度NSPFB分解后的LSI,且当i=1时,LSI0表示的是原始乳腺X线图像;函数H0(z)是二通道非下采样滤波器组NSPFB的带通分解滤波器。
定义2(带通子带图像BSI)

其中BSIi表示第i尺度NSPFB分解后的BSI,且当i=1时,LSI0表示的是原始乳腺X线图像;函数H1(z)是二通道非下采样滤波器组NSPFB的带通分解滤波器。
根据上述描述和以前的研究成果表明,此多分辨率图像分解方法能够有效检测乳腺病变,成功分类可疑病变和乳腺组织[13]。
第二阶段将使用Z-Moments对第一阶段所获得的子图进行特征提取,这种方法已经被广泛应用于病变的形状分析[6,14],因为形状对于确定乳腺癌病变的恶性程度是至关重要的[15]。针对每一个由原始乳腺X线图像分解得到的子图,都从中提取32个高维的泽尼克值,因此一张原始乳腺X线图像可以提取到480个特征值。如图1所示。
最后将所提取的480个特征值通过SVD分解进行特征的约简,以获得维度较小的但可以概括全局的特征。因为分类器的学习通常是一个耗时的事情,它可能涉及训练数据的多次迭代[16],涉及到与不同的随机初始条件相结合的交叉验证,测试不同的内核(学习函数),且数据量越大,耗时就会越多。因此本文采用SVD方法提取重要的可以概括全局的特征,从而减少数据量以减少耗时。
以上就是对图1所示的框架的介绍,与其他目前最先进的方法相比,其在准确率和时间效率上都取得了显著的成效。
4 特征提取阶段
下面将详细介绍基于NSCT特征提取的过程和Z-Moments的构建,以及SVM的分类算法流程。
4.1 基于NSCT的特征提取
NSCT是2005年由Cunha等人提出的一种具有平移不变性的轮廓变换[17],其是基于NSPFB和NSDFB的一种变换。下面将详细介绍这两种方法。
4.1.1 非下采样塔式滤波器
非下采样塔式滤波器(NSPFB)不同于2004年由Do和Veterli提出的一种能够较好表示二维信号的数学工具——轮廓变换法中的拉普拉斯金字塔(Laplacian pyramid,LP)多尺度分析[18]。因为LP多尺度分析和离散小波变换在分解原始乳腺X线图像时都采用下采样的方式,导致多尺度分解后的低频图像和高频图像都没有原始图像的尺寸大小,即原始图像的下采样过程在滤波器中会失真,因此使用LP多尺度分解或者离散小波变换都缺乏平移不变性。而NSPFB取消其分解过程中对信号进行的下采样操作,对滤波器进行相应的上采样(插值)操作,减少了原始乳腺X线图像在多尺度分解过程中的失真。
图2给出了一个三层NSPFB的分解过程[18]。通过图2可以看出,每一张乳腺X线图像经过NSPFB都分解为不同尺度的图像。第一尺度分解得到LSI1和BSI1,第二尺度分解得到LSI2和BSI2,以此类推。

Fig.2 NSPFB decomposition process图2 NSPFB分解过程
4.1.2 非下采样方向滤波器
非下采样方向滤波器(NSDFB)是一个双通道的滤波器组,其主要功能是将NSPFB所得的BSI进行树状结构分解。并且BSI若通过一个l元的树状结构分解,则有效地将信号分成了2l个子带,其频带被分割成楔形。离散小波变换也可以进行此过程,但离散小波变换只能提取水平、垂直和对角线3个方向的细节图像,而NSDFB能提取多个方向的细节图像。每个由NSDFB得到的方向子图都和原始乳腺图像大小相同,而不同于离散小波变换的所有带通方向子图之和等于原图。
定义3(带通方向子带图像BDSI)
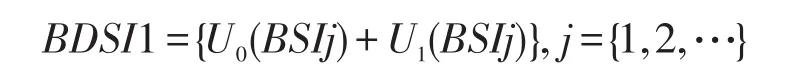
此表示对BSIj进行1级方向分解,将得到2个BDSI1。其中BSIj表示第j尺度NSPFB分解后的BSI,若对BSIj进行2级方向分解,则得到4个BDSI2,其表达式为:

对BSIj进行m级方向的分解以此类推。
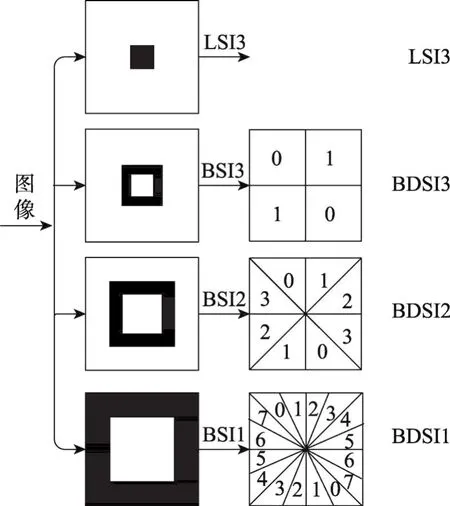
Fig.3 NSDFB decomposition process图3 NSDFB分解过程
如图3,展示的是对不同尺度的BSI进行不同方向分解的过程,因为BSI1相比其他BSIi(i≠1),其图像的结构、轮廓、纹理最为清晰,和原始图像细节最相近,所以对其进行3级方向分解,得到8个BDSI3;BSI2进行2级树状结构分解,得到4个BDSI2;BSI3进行1级树状结构分解,得到2个BDSI1;而最后的LSI3,和原始图像最相似,其不进行树状结构的分解,可直接进行泽尼克矩的构建[18]。
4.2 构建泽尼克矩
通过三层的NSCT将得到的LSI3和所有的BDSI1、BDSI2、BDSI3都作为构建泽尼克矩(Z-Moments)的输入图像。每张原始图像经NSCT分解后都会扩展为15张子图,且其中每个子图都可以构建出有32个值的Z-Moments。Z-Moments的计算过程包括3个步骤:径向多项式的计算,Zernike基函数的计算以及将图像投影到Zernike基函数上的Z-Moments的计算[18-21]。
从输入图像获得Z-Moments的过程开始于Zernike径向多项式的计算[21]。实值一维的径向多项式Rn,m定义为式(6):
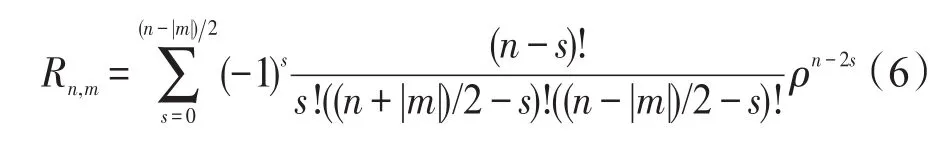
其中,n是非负整数;m是整数,且m满足n-|m|=偶数,|m|≤n;ρ是从原点到向量(x,y)的长度[18,22]。
根据式(6)可知,由单位圆定义的复值二维Zernike基函数为:

复值二维Zernike多项式满足下式正交条件:
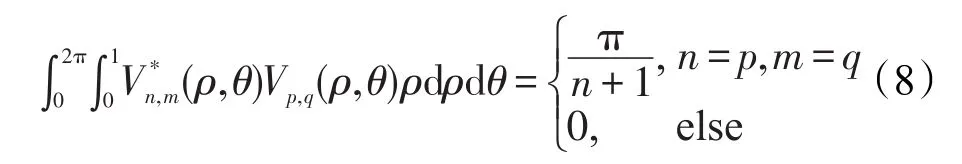
其中,*表示共轭复数。如前所述,正交性意味着在不同的n、m组合成的不同的矩的图像信息是非冗余非重叠的。这个属性使得每个组合的贡献是独一无二的,独立于图像中的信息[19]。其实不同组合形成的特征都具有同样的重要性。由n、m形成的复合Z-Moments被定义为[21]:
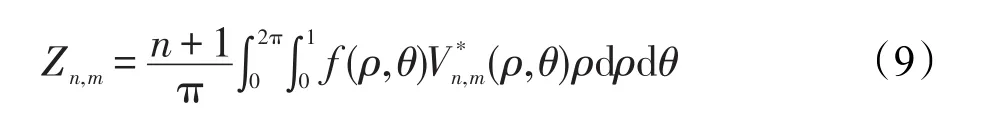
Fig.4 Original image normalized map图4 原始图像归一化映射图
其中,f(c,r)是图像函数,对于数字图像来说,式(9)中的积分可以由求和来代替。此外,图像的坐标必须通过映射变换归一化为[0,1]。图4描绘了映射变换的一般情况。注意,在这种情况下,位于圆的外侧的像素不参与Z-Moments的计算。最终,尺寸为N×N的图像的Z-Moments的离散形式化表示如下[23]:

其中,0≤ρcr≤1和λπ是归一化因子,在Z-Moments的离散实现中,归一化因子必须是通过映射变换到位于单位圆中的所有像素数,其对应于连续域中单位圆的面积[18]。像素(c,r)处的变换距离ρcr和相位θcr由下式给出。请注意,c和r分别表示图像的列数和行数。
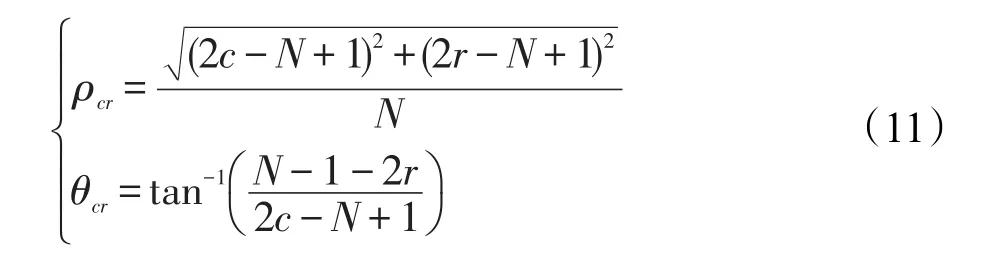
使用式(10)和(11),可以得到只有c、r、m和n的函数的最终方程。事实上,如果图像ROI(region of interest)区域的行数和列数是奇数,它将具有如下协调中心点:

结合式(11)、(12)可以得到以下的初值:
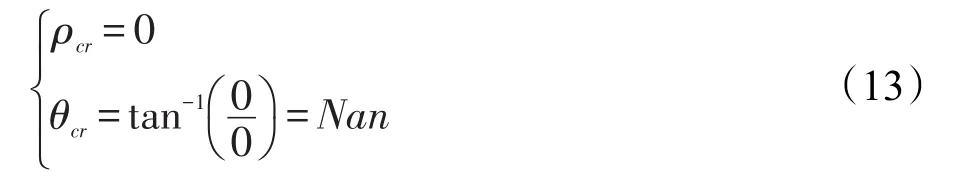
实际上,相位值是未定义的,解决问题的最佳方法是选择图像的行数和列数为偶数。因此,图像将不会有一个中心,并且问题的解将不含任何冗余。
本文选用的是高阶Z-Moments,虽然相比于低阶Z-Moments,高阶Z-Moments不仅有较高的计算复杂度[18,22],且其对噪声的敏感度也较高,因此如果没有精确地选择,可能会降低系统的性能。但是,由于高阶Z-Moments比低阶Z-Moments能更好地描述形状和边缘特征,为了更准确地分析图像的轮廓,本文选择了高阶Z-Moments。表1给出了高阶Z-Moments的n和m的取值。
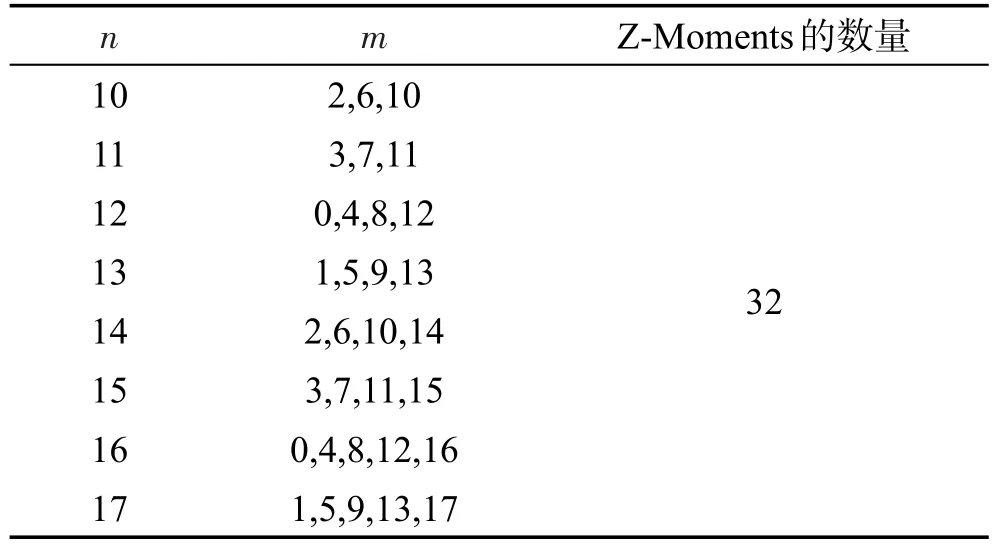
Table 1 Value status table ofn,m表1 n、m取值状况表
通过表1给出的n和m的值,可以从每张低频图像或者高频图像中得到32个值组成的Z-Moments。
4.3 支持向量机的分类
分类算法有很多,本文采用支持向量机(SVM)分类方法,因为通过实验分析,使用SVM的分类效果最好。并且通过Z-Moments的特征提取过程,每张原始的乳腺X线图像都有32×15=480个特征,但因为并不是所有的特征都对图像的分类有用,所以使用SVD方法约简特征,提取可以代表总体95%以上的图像信息的前K个值。这样既减少了数据量,缩短了分类的训练时间,又提高了分类的准确性。SVM的思想是把输入向量映射到高维特征空间,然后在这个高维空间中构造最优分类面,原本线性不可分的问题在高维空间中转化为线性可分。同时为避免出现“维数灾难”,又引入核函数K(xi,xj)=ϕ(xi)ϕ(xj)代替内积运算。
SVM巧妙地解决了高维、非线性问题,且推广性好,存在唯一解。算法1是SVM的算法流程。
算法1基于SVM的分类方法
输入:乳腺X线图像经过预处理、特征提取和SVD分解后得到的特征数据集Fc={zm1,zm2,…,zmn}。
输出:乳腺X线图像所属类别(正常,良性,恶性);训练时间(Train-time),预测时间(Test-time),预测的准确率(Test-rate)。
1.For(i=1;i 2.Read(zmi) 3.Split(Fc)为训练集(TrainFc)和测试集(TestFc) 4.对于TrainFc让其作为SVM模型的输入数据进行训练,计算Train-time并输出 5.基于训练完成的SVM模型,把TestFc作为输入,输出测试这些TestFc应该所属的类别,计算并输出Test-time 6.输出预测类别和真实类别之间的Test-rate 本文使用255张IRMA数据库的脂肪型乳房组织图像,其中233例正常病例(无病变)、72例良性病例和83例恶性病例[10]。IRMA数据集文档不仅详细介绍了各乳腺X线图像成像的扫描方法,还介绍了成像方向是右乳房还是左乳房,对其乳腺病变按照BIRADS的标准分类为良性、恶性、正常[15]。然而,在乳腺X线图像中经常会有人造伪影的存在,例如由指纹引起的常见的凹槽和油脂等,这会给图像的处理带来困难。IRMA数据库通过使用专业临床知识选择的感兴趣区域(ROI)来避免这些情况。 Fig.5 Original breast image图5 原始乳腺图像 图5是IRMA中的8张原始图像,其中有左右不同方向的对比图。当然IRMA医学图像数据库还提供了钙化、结构扭曲和不对称等乳腺X线图像情况,但本文仅针对处理脂肪型乳腺组织的乳腺X线图像。另外,为了在分类应用中使用IRMA数据库,有必要平衡数据集,因此本实验还分别合成了161个良性病例和150个恶性实例。合成方法是基于真实图像特征实例来创建人造实例。 为了验证基于NSCT的乳腺X线图像的分类方法的高效性,本文主要与Sidney等人的实验结果做比较。因此实验采用了不同的分类器或者同种分类器的不同核函数,组合各种不同的处理过程,形成比较实验。 表2列出了各种实验方法。其中加黑的实验方法是本文提出的组合方法,一共4种,接下来将基于这4种类型来分析实验结果。 基于表2中的16种实验方案,本文首先考虑测试集分类结果的准确率,这也是能直观地说明本文方法优于其他方法的指标。 从图6中可以看出,对于SVM的核函数无论是使用linear、polynomial、RBF,或者决策树,相比较而言都是本文方法的准确率更高。对于Sidney所提出的3种不同的离散小波变换,选择Symlet8波的效果在各种分类方法中最优。另外,对于本实验而言,SVM的核函数在选取linear和polynomial时都有较好的实验效果,并且linear核函数的实验效果更优。 Fig.6 Accuracy of test set图6 测试集的准确率 Table 2 Experimental methods表2 实验方法 在注重实验准确率的同时,时间效率也是不可忽略的指标。一个好的分类方法需要综合考虑准确率和时间效率,在平衡两种指标使分类效果达到最优的情况下,才更可能在实践中有所应用。图7给出了各种分类方法的训练时间。 从图7中可以看出,本文方法无论采用哪一种分类方法,其训练集所需的训练时间都明显低于Sidney所提出的3种类型的小波变换。原因在于不同于Sidney等人提出的方法,在特征提取阶段本文方法并没有直接将所得数据作为各种分类器的输入,而是首先对数据进行奇异值分解,从而降低了数据的维度,提高了训练时间的效率。因而本文方法在一定程度上是具有实践意义的。 Fig.7 Training time图7 训练时间 总之,在本文所实现的4种类型的16种实验方法中,无论是本文提出的实验方法,还是Sidney等人提出的实验方法,SVM的linear核函数的方法取得了最好的分类效果。并且针对Sidney等人提出的利用离散小波变换分解图像,也做了基于不同类型的小波变换的对比实验,并且实验效果表示,Sidney提出的Symlet8型离散小波变换具有最好的实验效果,但都不如本文提出的NSCT方法。其主要是由于本文在特征提取阶段采用了高阶Zernike矩,比Sidney等人所采用的低阶Zernike矩能提取到更多能够代表乳腺X线图像的特征,并且通过SVD分解使得特征更具代表性,数据量大大减少,在时间效率上也有很大的提升。 本文提出了一种基于NSCT的乳腺X线图像的分类方法。该方法首先经过NSCT分解将乳腺X线图像的感兴趣区域分解为多分辨的子图,然后用泽尼克矩提取子图中的特征,另外在数据预处理阶段选用了奇异值分解对特征进行约简,以提取重要的可以概括全局的特征。本文方法组合了纹理和形状特征,使用基于SVM的分类算法将乳腺X线图像分类为正常、良性和恶性,实现了乳腺病变的检测和分类。考虑到BIRADS标准,本文将兴趣类别定义为正常(无损伤的乳腺组织)、良性和恶性病变3种分类。通过数学形态学的理论依据证明了模式谱是二值图像的理想和唯一的形状表示。并且本文还使用形态学光谱进行了特征提取实验,并对其进行了评估。实验过程结合了4种类型的分类方法的16种不同算法。 基于本文方法的思想可以在很大程度上处理更加困难的乳腺X线图像,如致密、极度密集和纤维腺性乳腺组织。未来加以改进其也可以应用于其他形式的癌症诊断,或者其他相关的生物医学图像分类问题,如脑磁共振成像、免疫组织化学图像,以及其他形态和纹理都必不可少的复杂的图像分析问题。本文分类方法的总体精度较高,训练时间相对较低,便于快速推广并帮助医生准确诊断病情。 [1]Statistical data for breast cancer,from IARC(International Agency for Research on Cancer)[R].WHO(World Health Orgnization),2013. [2]Rizzi M,D'Aloia M,Castagnolo B.Computer aided detection of microcalcifications in digital mammograms adopting a wavelet decomposition[J].Integrated Computer-Aided Engineering,2009,16(2):91-103. [3]Rizzi M,D'Aloia M,Castagnolo B.A supervised method for microcalcification cluster diagnosis[J].Integrated Computer-Aided Engineering,2013,20(2):157-167. [4]Wang Zhiqiong,Yu Ge,Kang Yan,et al.Breast tumor detection in digital mammography based on extreme learning machine[J].Neurocomputing,2014,128(5):175-184. [5]Tahmasbi A,Saki F,Shokouhi S B.Classification of benign and malignant masses based on Zernike moments[J].Computers in Biology&Medicine,2011,41(8):726-735. [6]Saki F,Tahmasbi A,Soltanian-Zadeh H,et al.Fast opposite weight learning rules with application in breast cancer diag-nosis[J].Computers in Biology&Medicine,2013,43(1):32-41. [7]Rouhi R,Jafarib M,Kasaeic S,et al.Benign and growing and CNN segmentation[J].Expert Systems with Applications,2015,42(3):990-1002. [8]de Lima S M,da Silva Filho A G,dos Santos W P.Detection and classification of masses in mammographic images in a multi-kernel approach[J].Computer Methods and Programs in Biomedicine,2016,134:11-29. [9]Soille P.Morphological image analysis principles and applications[J].Sensor Review,2003,28(5):800-801. [10]Hänni M,Lekka-Banos I,Nilsson S,et al.Quantitation of atherosclerosis by magnetic resonance imaging and 3D morphology operators[J].Magnetic Resonance Imaging,1999,17(4):585-591. [11]Thanh N D,Binh V D,Mi N T T,et al.A robust document skew estimation algorithm using mathematical morpholgy[C]//Proceedings of the 19th IEEE International Conference on Tools with Artificial Intelligence,Patras,Oct 29-31,2007.Piscataway:IEEE,2007,1:496-503. [12]Santos W P,Mello CAB,OliveiraAL I.Mathematical morphology[M]//Digital Document Analysis and Processing.New York:Nova Science,2011:159-192. [13]Gefen S,Tretiak O J,Piccoli C W,et al.ROC analysis of ultrasound tissue characterization classifiers for breast cancer diagnosis[J].IEEE Transactions on Medical Imaging,2003,22(2):170-177. [14]Tahmasbi A,Saki F,Shokouhi S B Z Z.Classification of benign and malignant masses based on Zernike moments[J].Computers in Biology&Medicine,2011,41(8):726. [15]BI-RADSTM(breast imaging reporting and data system)[R].American College of Radiology,2003. [16]Liang Nanying,Huang Guangbin,Saratchandran P,et al.A fast and accurate online sequential learning algorithm for feedforward networks[J].IEEE Transactions on Neural Networks,2006,17(6):1411-1423. [17]CunhaA L,Zhou J P,Do M N.The nonsubsampled contourlet transform:theory,design,and applications[J].IEEE Transactions on Image Processing,2006,15(10):3089-3101. [18]Hwang S K,Kim W Y.A novel approach to the fast computation of Zernike moments[J].Pattern Recognition,2006,39(11):2065-2076. [19]Vapnik V N.The nature of statistical learning theory[M].New York:Springer-Verlag,1995. [20]Li Shan,Lee M C,Pun C M.Complex Zernike moments features for shapebased image retrieval[J].IEEE Transactions on Systems,Man,and Cybernetics:Part A Systems and Humans,2008,39(1):227-237. [21]Li Xin,Song Aiguo.A new edge detection method using Gaussian-Zernike moment operator[C]//Proceedings of the 2nd International Asia Conference on Informatics in Control,Automation and Robotics,Wuhan,Mar 6-7,2010.Piscataway:IEEE,2010:276-279. [22]Wee C Y,Raveendran P,Takeda F.Fast computation of Zernike moments for rice sorting system[C]//Proceedings of the 2007 International Conference on Image Processing,San Antonio,Sep 16-19,2007.Piscataway:IEEE,2007:165-168. [23]Tahmasbi A,Saki F,Shokouhi S B.An effective breast mass diagnosis system using Zernike moments[C]//Proceedings of the 17th Iranian Conference on Biomedical Engineering,Isfahan,Nov 3-4,2010.Piscataway:IEEE,2010:1-4.5 数据集及实验结果与分析
5.1 数据集

5.2 实验结果与分析
5.2.1 测试集准确率的分析


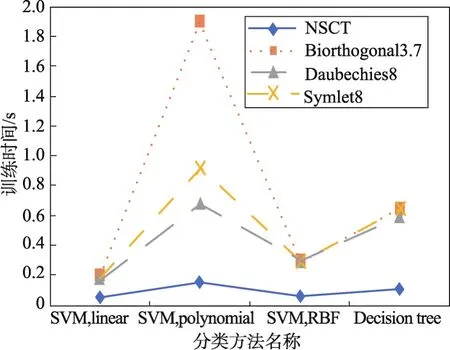
5.2.2 训练集的时间分析
6 结论

