基于优势关系粗糙集和可拓理论的供应商选择方法

许文亮，杨玉中，吴立云，赵　静　XU Wenliang,YANG Yuzhong,WU Liyun,ZHAO Jing

（河南理工大学 能源科学与工程学院，河南 焦作 454000）

(School of Energy Science&Engineering,Henan Polytechnic University,Jiaozuo 454000,China)

0　引言

供应链管理作为20世纪90年代新兴的管理模式，在适应激烈的市场竞争环境和应对多变的客户需求方面有着不容忽视的优势。而供应商作为供应链管理的一个重要组成部分，客观、科学地对供应商进行评选是做好供应链管理、实现供应链价值最大化目标的基础和前提。对于供应商综合能力评选的研究，重点在于两个方面，一是如何让综合评价指标体系尽可能的完整、科学、全面；二是如何让评价方法更为科学、适用。国内外的学者分别从这两方面进行研究，并取得了令人瞩目的成果。

对于评价指标体系的研究，美国的Dickson G.W.[1]首次系统地对供应商评价问题进行了研究，他通过问卷调查的方式分析总结出了23条供应商综合能力评价指标和其重要性排序。在此基础上，学者们从采购物品的属性、供应商所在的行业以及绿色环保等方面进行了研究，对供应商综合能力评价指标及其重要性做出了相应的修改和完善。其中，Choi T Y[2]将供应商同核心产业的关系考虑进去，将供应商的合作关系及潜力补充到综合评价指标中；马士华、林勇[3]等人将综合评价指标进行了分层，下层指标是对上层指标更为细致的描述，且下层指标值的获取更为直接、客观。目前应用的指标体系都是根据具体问题而建立的，想要得到一个能够满足不同领域供应商要求和客户需求的综合评价指标体系，仍需进行不断研究。

对于评价方法的研究，众多学者分别以定性、定量以及定性和定量相结合的分析法提出了众多评价方法。定性的方法主观性太强，定量的方法又过于依赖数据，数据的剧烈变化对结果的影响过大，只有定性和定量相结合的方法才能相互取优，使评价结果更为科学、准确。现有较为成熟的评价方法有很多，各有优势。T.L.Saaty[4]提出的层次分析法利用决策问题的层次结构，将专家们的主观评价值通过数学化的思维过程去确定下层各元素对应上层元素的权重，再根据加权值的大小做出决策。模糊综合评价法和灰色关联法同层次分析法一样，都是先建立决策问题的层次结构，再求出下层各元素对应上层元素的权重，最后比较加权值的大小来作出决策；不同的是，模糊综合评价法通过建立隶属函数来实现评价值定性到定量的转换，灰色关联法根据两个元素间变化趋势建立关联函数并以此来确定彼此间的关联度。由于隶属度函数、关联函数以及判断矩阵的取法不尽相同，也没有一个统一的标准，因此各类改进的层次分析法、改进的灰色关联法、改进的模糊综合法以及三种方法的混合使用大量出现。如彭聪[5]将灰色关联法和层次分析法结合使用，用灰色多层次评价方法对供应商进行了选择。在出现大量评价方法的基础上，学者从不同方面入手研究：叶斌[6]通过指标信息熵值的效用价值确定了内河水运可持续发展能力的评价指标权重，这类研究注重应用科学的方法来确定权重，从而使评价更科学，类似的方法有粗糙集理论、熵增原理等；缪琳[7]运用物元和可拓理论将供应商的风险进行分级和排序，这类研究注重指标值的判别方法，从而使评价更合理，类似的方法有TOPSIS、可拓理论等；李武[8]提出的基于群体理想解的供应商选择多属性决策，这类研究注重集合决策者们意见，从而使评价更能满足需求，这类方法主要有群决策理论等。

本文运用粗糙集理论的科学方法来确定评价指标的客观权重，可拓理论的判别方式来给出评价结果。该方法通过原始数据直接获得指标的客观权重，再将决策组评价值区间化，最大程度上进行综合评价，最后做出决策选择。

1　供应商评价指标体系

作为供应商综合能力评价研究的重点之一，构建一个科学的供应商评价指标体系是评价方法能够应用的基础和前提，但不作为本文研究内容。本文直接选取了一个供应商评价指标体系作为应用。汽车工业绿色供应商选择的指标体系如表1[9]所示。

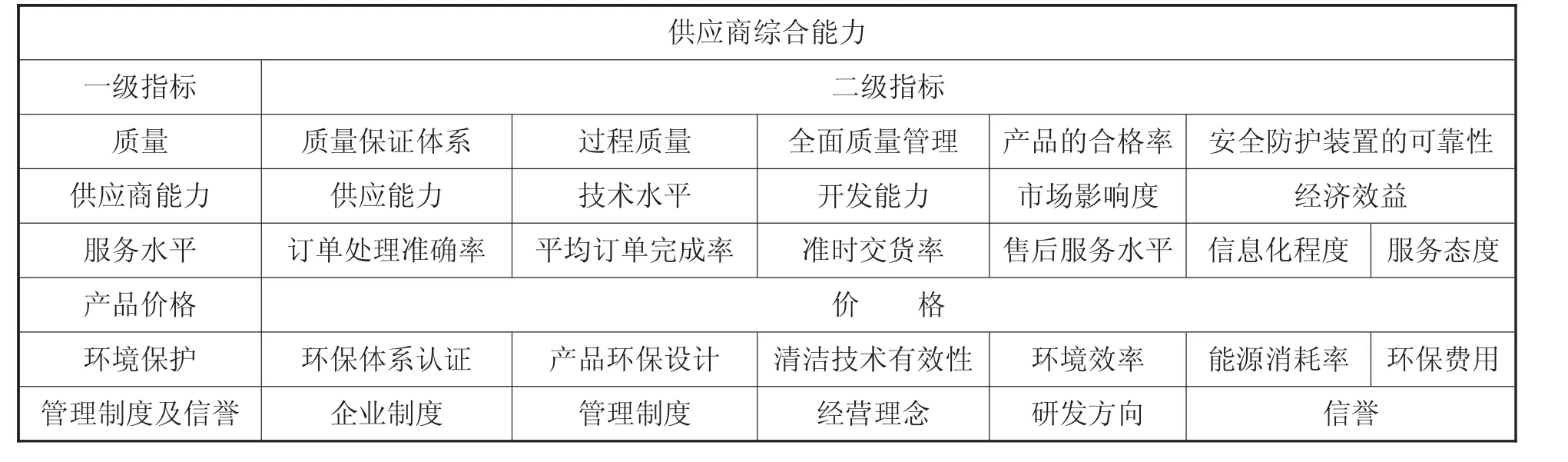
表1　绿色供应商选择的指标体系

2　基于粗糙集和可拓理论的选择方法

供应商评选方法也是供应商综合能力评价研究的重点之一，本文将粗糙集理论和可拓理论的优势结合起来，形成一种新的评价方法。

因为原始数据的量纲不同，且优势关系粗糙集是针对有序的排列，所以对于原始数据，必须要进行预处理使其规范化。

对于数值越大越优的指标：

对于数值越小越优的指标：

其中：i=1,…,m；j=1,…,n。

2.1　优势关系粗糙集确定指标权重

（1） 序信息系统

（2） 优势关系

在序信息系统中，如果B⊆A,x≥By，那么x在B上对y具有优势，记为。称为有序信息系统上的优势关系，其中B⊆A。设B=B1∪B2，其中B1是上向的属性集，B2是下向的属性集[11]。定义对象x在属性集B上的优势集合：

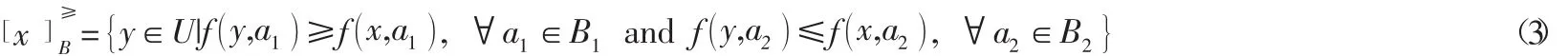
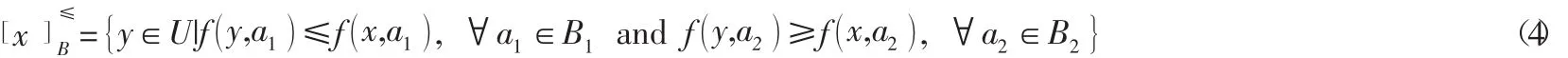
（3） 优势度

对xi,xj∈U利用粗糙集方法计算对象xi在属性集B下优于对象xj的程度为：

RBxi（）的值越大，对象xi在属性集B下越具有优势。按照RBxi（）由大到小排序可以得到对象在属性集B下的优劣次序，记为在属性集B条件下排序得到的一组秩[12]。

（4） 重要性

（5） 归一化确定权重

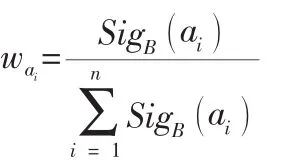
（8）

2.2　可拓判别方法选择供应商

可拓判别方法的基本思想是：根据供应商管理中各指标的实际数据分析，给出一个合理的若干等级划分，由专家意见或是数据库来确定各等级的数据范围，再将待评价对象的数据代入到各等级的集合中进行评定，根据它与各等级集合的综合关联度来确定它的等级，即与哪个等级综合关联度越大，说明它属于那个等级；同等级的综合关联度越高，说明它与该等级集合的符合程度越好。

（1） 构建评价值矩阵

决策组成员对各方案进行指标评价，评价值采用统一标准评分，构建评价值矩阵：

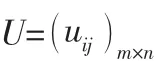
式中：X0=＜a,b＞，X=＜c,d＞，X0⊂X，且无公共端点；

（2）分别计算各方案的关联度

ρ（ x,X0）为点x与区间X0=＜a,b＞的距离；D（ x,X0,X ）为点x关于区间套的位值，即：

则称K（）x 为x关于区间X0，X的关联函数[9]。

（3）分别计算各方案综合关联度

其中：i=1,2,…,m。W是目标权重向量，K是关联函数。

（4）根据综合关联度，确定各方案的优先序。

3　算例分析

某公司计划对某重要部件进行采购，经过该公司成立的供应商选择小组的初选，计划对10家供应商（分别用A～J来表示）进行评价选择，采用表1的评价指标，待选供应商的原始数据和专家评分均取自吴立云、杨玉中[13]的《基于粗糙集—熵理论的绿色供应商选择模型研究》一文中的数据。

3.1　优势关系粗糙集确定客观权重

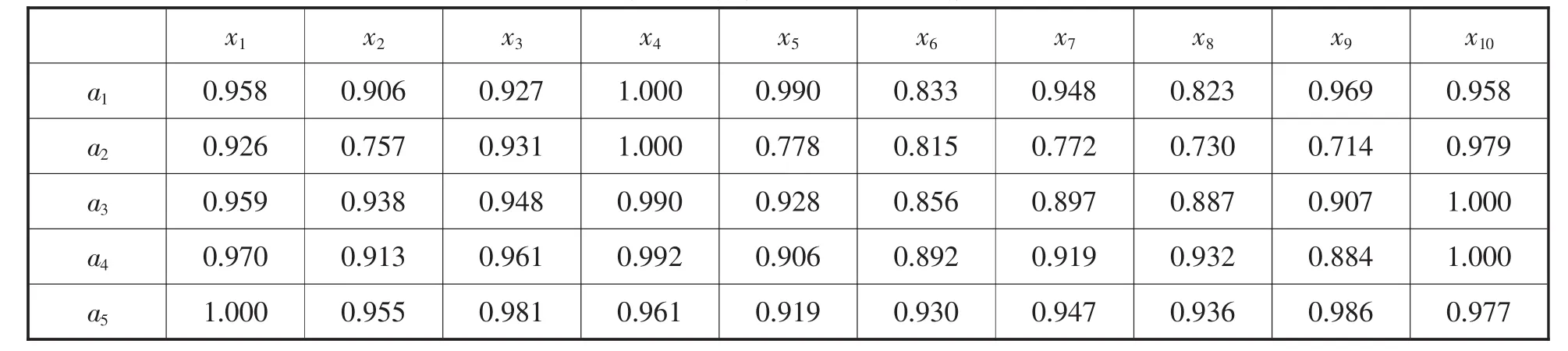
表2　质量指标值规范化处理后信息表

（2） 根据式（3）、式（4） 确定优势关系序数集

（3） 根据式（5） 计算相互优势程度矩阵

（4） 根据式（6） 计算综合优势度

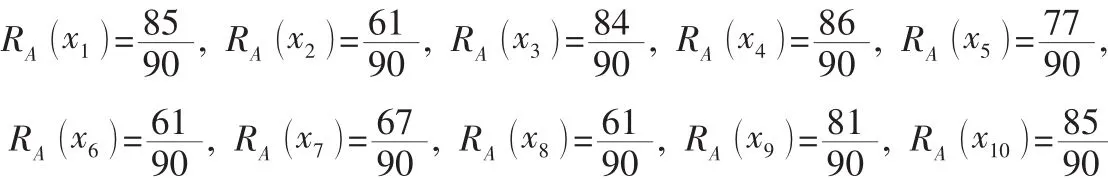
（5）综合优势度重新排序

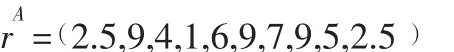
（6）同理计算各条件属性缺失情况下的新秩

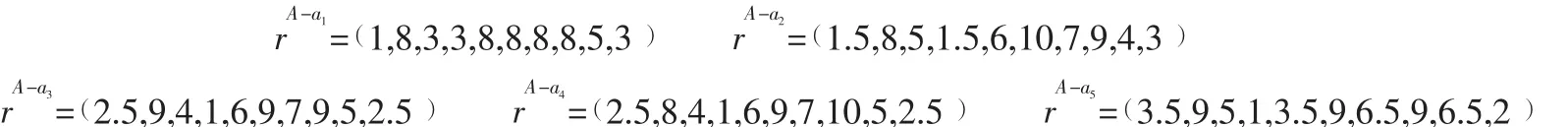
（7） 根据式（7） 计算各条件属性的重要度

“我们建立了学校国防教育基地，与洪洞红军八路军纪念馆结对子，与派出所建立共建单位，邀请所长担任学校国防教育校外辅导员。咱白石小学国防教育的成绩离不开这里得天独厚的红色革命资源，可以说是立足本地，挖掘本校和本地的地方资源来对学生进行国防教育。”程主任打开了话匣子，继续为编辑介绍。

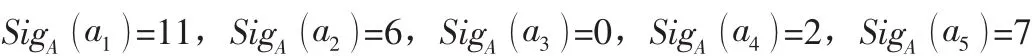
（8） 根据式（8） 计算指标权重

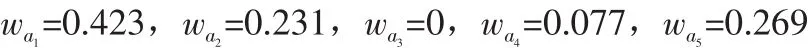
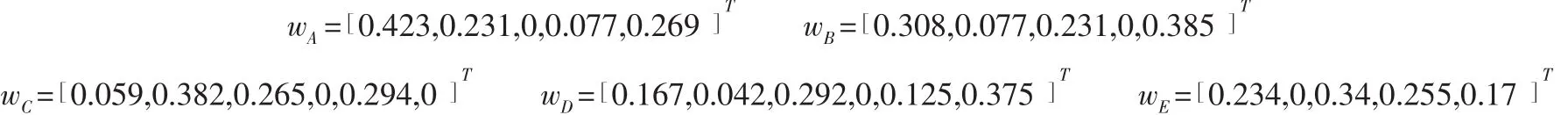
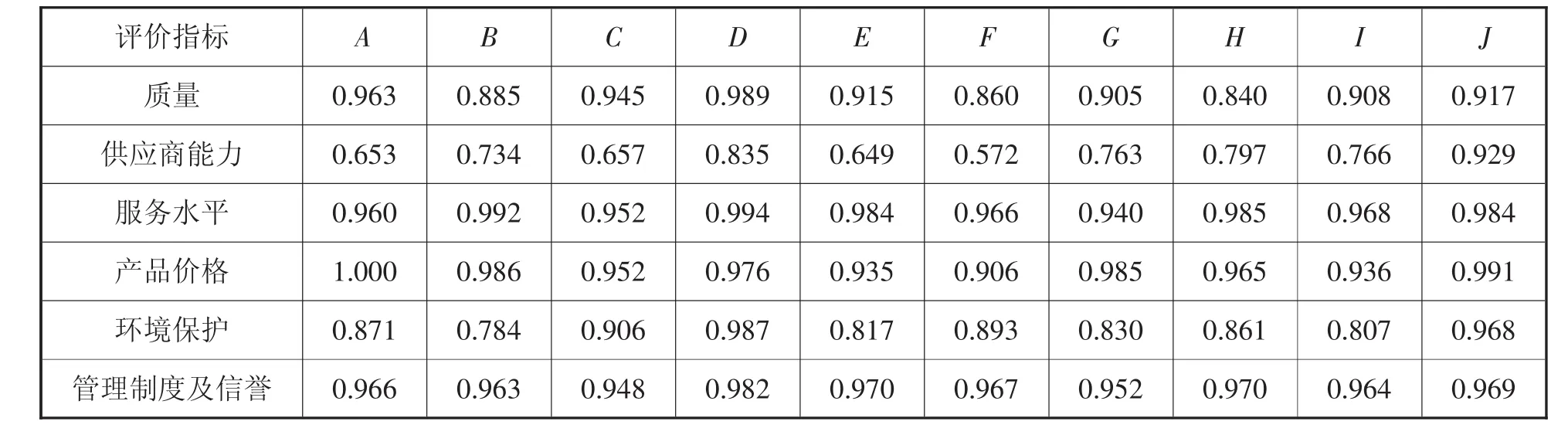
表3　供应商一级指标信息表

同理，使用优势关系粗糙集可以得到一级指标的客观权重为：

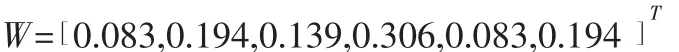
3.2　可拓判别方法选择供应商

（1） 构建评价值矩阵

评价值采用统一标准评分，评价值取0～10之间，并划分8～9.9之间的为好，5～8之间的为一般，1～5之间的为差，获得的评价值矩阵为：

（2） 计算关联度

由可拓理论确定的经典域和节域：

根据式（9）、式（10）、式（11） 计算关联度：

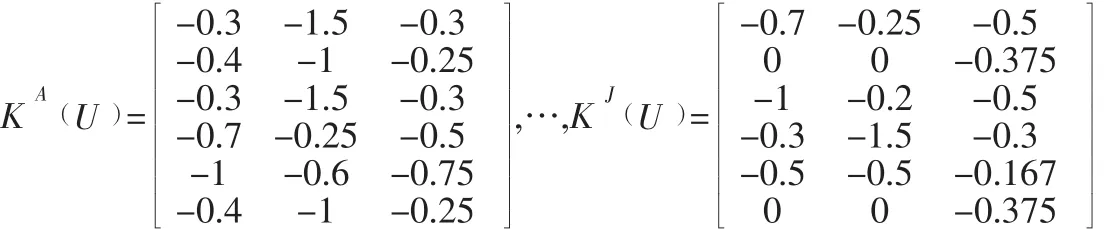
式中：KA（）U 表示对A供应商的各项指标关于三个等级的关联度。

（3） 计算综合关联度

根据式（12）计算综合关联度：

（4）对总评价值进行优先排序

根据评价准则可知，供应商A、B、D、H和I属于好，供应商C、E、G属于一般，供应商F、J属于差。根据总评价值的大小，所有供应商的优劣顺序为：

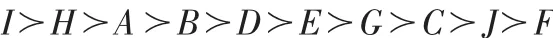
4　结论

通过结合应用粗糙集和可拓理论的方法对供应商进行评选，可以得出如下结论。

（1）基于优势关系粗糙集和可拓理论的方法可以给出参选供应商的等级划分，以及在各个等级中的分值大小。

（2）运用优势关系粗糙集对权重确定的客观性，可拓理论以区间描述主观评价的不确定性，结合了主、客观意见，使最终结果更加合理。

（3）结合可拓理论方法的应用，可以充分发挥可拓理论区间等级划分的优势。

（4）在应用优势关系粗糙集确定权重的过程中，出现了某些指标权重为零的现象，说明该模型还需要进一步进行改进。

参考文献：

[1]Dickson G W.An Analysis of Vendor Selection Systems and Decision[J].Journal of Purchasing,1966,2(15):1377-1382.

[2]Choi T Y,Hartley J L.An exploration of supplier selection practices across the supply chain[J].Journal of Operations Management,2012,14(4):333-343.

[3] 林勇，马士华.供应链管理环境下供应商的综合评价选择研究[J].物流技术，2000(5):30-32.

[4]Saaty T L.Decision making for leaders:the analytical hierarchy process for decisions in a complex world[J].European Journal of Operational Research,1982,42(1):107-109.

[5] 彭聪.灰色多层次评价方法在战略供应商选择中的应用[J].重庆交通大学学报（社会科学版），2012(1):60-63.

[6] 叶斌.基于改进熵值法的内河水运评价研究[D].成都：成都理工大学（硕士学位论文），2012.

[7] 缪琳.基于物元和可拓理论的供应商风险评价研究[D].大连：大连海事大学（硕士学位论文），2012.

[8] 李武.供应商选择群决策建模与多源多时段采购优化[D].武汉：华中科技大学（博士学位论文），2009.

[9] 吴立云，杨玉中.汽车工业绿色供应链管理理论及应用[M].北京：电子工业出版社，2015.

[10]张文修，梁怡，吴伟志.信息系统与知识发现[M].北京：科学出版社，2003.

[11]Greco S,Matarazzo B,Slowinski R.Rough sets theory for multi-criteria decision analysis[J].European Journal of Operational Research,2001,129(1):1-47.

[12]吕跃进，张旭娜，韦碧鹏.基于优势关系粗糙集的模糊综合评价的权重确定[J].统计与决策，2012(20):44-46.

[13]吴立云，杨玉中.基于粗糙集—熵理论的绿色供应商选择模型研究[J].工业工程与管理，2011,16(2):34-39.