基于模拟退火和粒子群改进的图像分割FCM方法

陆振宇 夏志巍 卢亚敏 黄现云

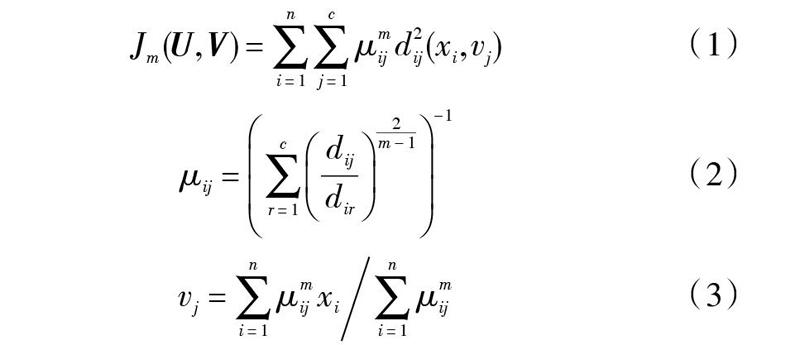
摘 要： 针对模糊C均值聚类（FCM）算法在分割图像时需要事先给出聚类数和容易陷入局部极小值的问题，提出一种新的FCM算法。首先，利用粒子群算法更新FCM的聚类中心，以加强算法的搜索能力，提高收敛速度；其次，根据模拟退火准则决定是否接受新的聚类中心，以得到当前迭代下的全局最优值；最后，设定有效性函数寻找图像的最佳聚类数，使算法具有自适应判断图像类别个数的能力。实验结果表明，该算法具有较好的全局收敛性，并且在未知聚类数的情况下能自适应寻找图像的最佳分类个数。

关键词： 自适应图像分割； 模拟退火算法； 粒子群算法； 模糊C均值； 聚类中心； 全局最优

中图分类号： TN911.73?34 文献标识码： A 文章编号： 1004?373X（2018）07?0036?05

Improved FCM method for image segmentation based on simulated

annealing and particle swarm optimization

LU Zhenyu1， 2， XIA Zhiwei1， LU Yamin1， HUANG Xianyun1

（1. School of Electronic & Information Engineering， Nanjing University of Information Science and Technology， Nanjing 210044， China；

2. Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment， Nanjing 210044， China）

Abstract： Since the traditional fuzzy C?means （FCM） algorithm needs to give the clustering numbers in advance and is easy to fall into local minimum for image segmentation， a novel FCM algorithm based on simulated annealing algorithm and particle swarm optimization （PSO） is proposed. The PSO algorithm is applied to update the clustering center of FCM to enhance the search ability and convergence rate of the algorithm. And then the simulated annealing rule is used to decide whether to accept the new clustering center or not， so as to obtain the global optimal value of current iteration. The validity function is set to find the optimal clustering numbers of the image， and make the proposed algorithm have the ability to adaptively judge the numbers of an image category. The experiment results demonstrate that the algorithm has perfect global convergence， and is able to adaptively find the optimum catelory numbers of the image in the case of the unknown clustering numbers.

Keywords： adaptive image segmentation； simulated annealing algorithm； particle swarm optimization； fuzzy C?means； clustering center； global optimization

0 引 言

图像分割是根据一定的准则把图像分割成几个互不重叠且各具特色的区域。目前图像分割方法主要有：基于阈值的分割方法，如最大类间方差的自适应阈值分割[1]、基于粒子群优化的多级阈值分割[2]；基于边缘检测的分割方法，如拉普拉斯算子[3]、结构化森林[4]；基于区域生长和分裂合并的分割方法，如区域生长与神经网络相结合的方法[5]、水平集与区域生长相结合的方法[6]；结合特定理论的分割方法，如基于分水岭的标号法[7]、深度卷积神经网络方法[8]。

聚类分割方法属于区域分割方法，它是一种无监督的统计方法，在图像分割领域应用非常广泛。FCM分割方法具有程序实现简单、不需要人为干预等方面的优势，但传统的FCM算法在求解目标函数时采用最速下降法，易使得迭代過程陷入局部最优解。此外，对图像进行分割前必须预先给出图像的聚类个数，可扩展性较差。

针对这些问题，许多学者提出了很多改进的方法。针对目标函数求解时易陷入局部极值的问题，文献[9]提出粒子群与FCM融合（PSOFCM）的方法；文献[10]提出捕食者?食饵者微粒群与FCM融合（PPPSOFCM）的方法。针对如何自适应判定图像最优聚类数的问题，文献[11]提出基于数据集模糊划分模式的划分系数来确定聚类数；文献[12]提出基于紧密度和分离度这两个指标的有效性函数[VXB]来确定最佳聚类数。

基于以上两个问题的综合考虑，本文提出一种自适应的模拟退火粒子群FCM算法，该算法在已有的FCM聚类算法中融合了模拟退火、粒子群和有效性函数。首先在优化FCM目标函数时，利用粒子群算法更新FCM的聚类中心。其次，根据模拟退火的Metropolis准则继续调整聚类中心，使得算法在每次迭代时都能达到全局最优。最后，引入有效性函数，通过计算图像在不同类别数下的有效值，判定图像的最佳聚类数，使得算法在未知类别数的情况下得到合理的分割结果，进一步提升算法的自适应性。利用改进的方法对仿真图像和自然图像进行实验，实验结果表明，本文算法不仅能够达到全局最优，而且可以在未知聚类数的情况下自动寻找图像的最佳分类个数。

1 FCM算法

FCM方法是将样本空间[X={x1，x2，…，xn}]的样本点分成[c]个类别， 其目标函数为：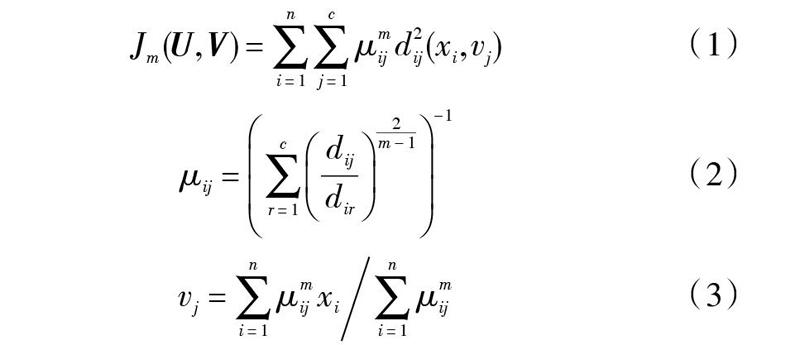

式中：[U=（μij）n×c]是隶属度矩阵；[μij]是样本点[xi]隶属于第[j] 类的值；[m（m>1）]是模糊指数；[V=（v1，v2，…，vc）]是聚类中心值的矩阵；[vj]表示第[j]个聚类中心；[d2ij（xi，vj）=xi-vj]是样本点[xi]到聚类中心[vj]的欧氏距离。

该算法首先确定聚类数[c]和初始化隶属度矩阵，然后通过式（2），式（3）反复更新聚类中心和隶属度矩阵，当达到一定精度时，就得到各类的聚类中心和隶属度。

该算法有以下缺点：对初始值敏感，很大程度上依赖初始聚类中心的选择，当初始聚类中心严重偏离全局最优聚类中心时，用FCM很可能陷入局部极小值。且必须预先给定聚类数[c，]但对于大多数样本往往不知道最佳聚类数。

2 PSOFCM算法

基于粒子群的模糊C均值聚类算法（PSOFCM）的图像分割通过PSO算法优化FCM的聚类中心，在一定程度上避免了传统的FCM对初始值敏感、容易陷入局部最优的缺点，同时图像分割的效果也得到了提高，性能也比传统的FCM方法更加稳定。

矩阵[Z=（Z1，Z2，…，ZN）T]是[N]个粒子的位置矩阵，其中[Zl=（zl1，zl2，…，zlc）]作为PSO中的一个粒子，表示一个聚类中心的集合。通过式（2）可以计算隶属度矩阵[U，]将FCM算法的目标函数作为PSO的适应度函数：

式中：[vlj]是第[l]个粒子的速度在第[j]维上的分量；[Pl=（pl1，pl2，…，plc）]是第[l]个粒子的最佳位置；[Pg=][（pg1，pg2，…，pgc）]是全体粒子的最佳位置；[w]是惯性系数；[c1，c2]是学习因子，一般取2。

该算法通过式（5），式（6）改变每个粒子的位置即聚类中心的取值从而产生多种聚类结果，直到找到可接受的簇中心，即适应度函数达到终止条件或整个循环达到最大循环次数。此算法与FCM算法的最大区别在于不再使用梯度下降方法而是使用PSO来确定聚类中心。

PSOFCM算法主要通过粒子群的速度和位置公式来更新FCM算法中的聚类中心，该算法加强了FCM的全局搜索能力并提高了收敛速度，但仍然没有有效解决FCM易陷入局部极值的问题和需要事先给定聚类数的缺点。

3 本文方法

首先在FCM算法中加入模拟退火粒子群算法，利用粒子群算法的速度公式更新FCM的聚类中心，并用模拟退火算法的Metropolis准则来判断是否接受新的聚类中心。然后引入有效性函数，计算不同聚类数下的最优值所对应的有效值。最后根据有效值得到最佳的类别数和最优的分割结果。

3.1 改进的模拟退火粒子群与FCM的融合（SAPSOFCM）

N. Metropolis等人在1953年提出模拟退火算法，其思想是通过模拟高温物体退火过程的方法来找到优化问题的全局最优或近似全局最优解。为了解决PSOFCM易陷入局部极值的缺点，在PSOFCM方法中引入模拟退火算法，即在每次迭代过程中，若粒子的适应度小于该粒子之前的适应度则接受新值，反之以概率[P（T）]来接受恶化解。

[P（T）=exp（-ΔfT）] （7）

式中：[T]为当前温度；[Δf=fit（U，Z（k）l）-fit（U，Z（k-1）l）]，[k]为迭代次数。

这样粒子的适应度会偶尔向增加的方向发展，有利于跳出局部极小区域。随着假想温度的降低，系统活动性降低，最终以概率1稳定在全局最优值。

SAPSOFCM方法步骤如下：

Step1：初始化参数，对初始温度[T0、]温度下降系数dec、群体规模[N、]学习因子[c1，c2、]惯性系数[w]等赋初值，粒子群的最大迭代次数为[kP，]模拟退火的最大迭代次数为[kS]。随机产生[N]个初始位置，設[k=1，][i=1]。

Step2：根据式（4）求出各粒子的适应值，若当前粒子的适应度小于该粒子最佳位置的适应度，则用[Zl]替代[Pl；][Pg]取所有粒子中适应度最小的最佳位子。

Step3：根据式（5），式（6）更新粒子群的速度及位置，并根据Metropolis准则决定是否接受新值。

Step4：若[fit（U，P（k）g）-fit（U，P（k-1）g）<ε]或[k>kP，]则进入下一步。否则转入Step2且[k=k+1]。

Step5：进行退火操作[T=dec?T]且令[k=0]。

Step6：若[i>kS，]则进入下一步；否则转入Step2且[i=i+1]。

Step7：得到最小有效值对应的隶属度矩阵，根据最大隶属度原则得到分割图像。

此方法在分割图像时用粒子群算法的速度和位置公式改变聚类中心，并用模拟退火算法的Metropolis准则来判断是否接受新的聚类中心，使得该方法能够以一定的概率跳出局部极值，从而达到全局最优值。

3.2 自适应的SAPSOFCM方法

虽然SAPSOFCM算法解决了模糊C均值聚类易陷入局部极值的缺点，但仍然需要预先给出聚类数。人们在给出聚类数时，往往凭借经验，有时并不能得到很好的分割结果。若在SAPSOFCM算法中引入有效性准则函数，则该算法能够自适应地找到最佳聚类数。

首先确定聚类数[c]的范围，因为图像最少要分成两类，最多分割成最大灰度值的根号，所以取[cmin=2，cmax=15。]然后在[c]取不同值的情况下调用SAPSOFCM方法分别对图像进行聚类，求出不同聚类数条件下的聚类中心值及其对应的隶属度矩阵。最后调用式（8）求出不同聚类数对应的有效值。最小有效值对应的聚类数即为最佳聚类数。

通过有效性准则函数确定最优聚类数，本文选取文献[13]提出的[VWSJ]函数进行仿真实验，其定义如下：

式中：[Pg=（Pgj）1×c]表示聚类中心向量；[Pgj]是第[j]个聚类中心；上标[S]表示样本空间[X]的维度；[xpj]表示数据[xj]的第[p]维值；[σ（X）p]表示样本集[X]的第[p]维数据方差，在本文中[X]是一维数据空间，即[S=1]。当[VWSJ（U，Pg，c）]达到最小值时，说明分类的效果最好。

3.3 方法步骤

综上，本文方法的总体步骤如下：

4 实验结果

本实验的测试环境为CPU酷睿2.5 GHz，内存8 GB，用Matlab 2012a编程实现。在合成图像和Berkeley大学数据库中的图像进行对比实验，以验证本文方法在图像分割中的效果。

其中，初始参数设置为[c1=1.9，][c1=1.8，][w=0.7，][N=30，][T0=5 000，]dec=0.9。

图1是对仿真图像的实验，以验证本文方法能否找到最佳聚类数。图1a）和图1c）是待分割图像，都包含5个区域，图1a）中5个区域的灰度值有较明显的差异，但图1c）中上面2个区域和中间圆形区域的灰度值非常接近。使用本文方法对图1a）和图1c）进行分割，其结果如图1b）和图1d）所示。从结果中可以看出，本文方法能自动检测出图中的5个区域，能够在未知聚类数的情况下自适应地得到最佳聚类数。

为验证本文方法的效果，选择经典的Camera和Berkeley大学图像库中一张自然图像176039进行测试。分别用本文方法，PSOFCM和FCM方法对这些图像分割3次。

图2，图3显示了不同方法在各个图像上的3次分割結果。其中第1行是原始待分割图像，第2行～第4行分别是本文方法，PSOFCM方法以及FCM方法得到的3次分割结果。

从图中可以看出，由PSOFCM方法和FCM方法得到的3个分割结果差异较大，且大部分分割结果不符合实际需求。而本文方法所得的分割结果符合人类视觉系统的特点，且3次分割结果非常接近。这些结果表明本文方法的分割结果非常稳定。

表1给出了不同方法在各个图像上运行3次所得的目标函数值，其中最优值用粗体标出。从表中可以看出，由本文方法所得的分割结果所对应的目标函数值最小，且3次都能达到最小。

5 结 论

鉴于FCM方法进行图像分割时有对初始值敏感易陷入局部极值且需要事先给出聚类数的缺陷，本文提出了基于模拟退火粒子群算法的自适应FCM方法。首先使用粒子群算法的速度公式和位置公式来更新聚类中心，加强算法的全局搜索能力，提高收敛速度；然后以模拟退火准则来判断是否为新的聚类中心，使得该方法能够以一定的概率接受恶化解，从而跳出局部极值的陷阱达到全局最优解；最后通过有效性准则函数来计算不同聚类数下的有效值，最小有效值所对应的聚类数则为最佳聚类数。通过合成图像的实验结果表明，本文方法能够在未知聚类数的情况下自适应地寻找最佳聚类数；对自然图像的分割结果表明，本文方法能够达到全局最优并且具有很好的稳定性。该方法具有一定的实用价值。

参考文献

[1] JUMB Vijay， SOHANI Mandar， SHRIVAS Avinash. Color image segmentation using k?means clustering and Otsu′s adaptive thresholding [J]. International journal of innovative technology and exploring engineering， 2014， 3（9）： 72?76.

[2] LIU Yi， MU Caihong， KOU Weidong， et al. Modified particle swarm optimization?based multilevel thresholding for image segmentation [J]. Methodologies and application， 2015， 19（5）： 1311?1327.

[3] KUMAR Kalyan， SASMITA Jena， SAROJANANDA Mishra. Edge detection of satellite images： a comparative study [J]. International journal of innovative science， engineering & technology， 2015， 2（3）： 75?79.

[4] DOLLAR P， ZITNICK C L. Fast edge detection using structured forests [J]. IEEE transactions on pattern analysis and machine intelligence， 2015， 37（8）： 1558?1570.

[5] ROUHI Rahimeh， JAFARI Mehdi， KASAEI Shohreh， et al. Benign and malignant breast tumors classification based on region growing and CNN segmentation [J]. Expert systems with applications， 2015（42）： 990?1002.

[6] ZHAO Yuqian， WANG Xiaohong， WANG Xiaofang， et al. Re?tinal vessels segmentation based on level set and region growing [J]. Pattern recognition， 2014， 47（7）： 2437?2446.

[7] ZHANG Xiaodong， JIA Fucang， LUO Suhuai， et al. A marker?based watershed method for X?ray image segmentation [J]. Computer methods and programs in biomedicine， 2014， 113（3）： 894?903.

[8] ZHANG Wenlu， LI Rongjian， DENG Houtao， et al. Deep convolutional neural networks for multi?modality isointense infant brain image segmentation [J]. Neuro image， 2015， 108： 214?224.

[9] 陈曦，李春月，李峰，等.基于PSO的模糊C?均值聚类算法的图像分割[J].计算机工程与应用，2008，44（18）：181?182.

CHEN Xi， LI Chunyue， LI Feng， et a1. Image segmentation based on PSO and fuzzy C?means clustering algorithm [J]. Computer engineering and applications， 2008， 44（18）： 181?182.

[10] 周鲜成，申群太.基于空间邻域信息的模糊聚类图像分割[J].武汉理工大学学报，2009，31（1）：102?105.

ZHOU Xiancheng， SHEN Quntai. Fuzzy C?means clustering algorithm based on spatial information for image segmentation [J]. Journal of Wuhan University of Technology， 2009， 31（1）： 102?105.

[11] BEZDEK J C. Pattern recognition with objection function algorithms [M]. New York： Plenum Press， 1981.

[12] XIE X L， BENI G. A validity measure for fuzzy clustering [J]. IEEE transactions on pattern analysis & machine intelligence， 1991， 13（8）： 841? 847.

[13] SUN H J， WANG S G， JIANG Q S. FCM?based model selection algorithms for determing the number of cluster [J]. Pattern recognition， 2004， 37（10）： 2027?2037.