基于广义延拓逼近的GPS卫星信号多普勒频移估计方法

唐青松 王兆瑞

摘 要：对并行码相位捕获GPS衛星信号时多普勒频移的栅栏效应进行研究。为了减小栅栏效应的影响，提高多普勒频移的捕获精度，提出用广义延拓逼近法来提高多普勒频移的估计精度，并在不增加算法运算量的基础上，对此方法进行优化，进一步降低了噪声对捕获多普勒频移精度的影响，仿真结果验证了该方法的有效性。

关键词： 栅栏效应； 多普勒频移； 广义延拓逼近； GPS； 卫星信号； 捕获精度

中图分类号： TN911.7?34 文献标识码： A 文章编号： 1004?373X（2018）07?0024?05

Doppler shift estimation method of GPS satellite signals

based on generalized extended approximation

TANG Qingsong1， 2， WANG Zhaorui2

（1. University of Chinese Academy of Sciences， Beijing 100012， China；

2. National Astronomical Observatories， Chinese Academy of Sciences， Beijing 100012， China）

Abstract： The picket?fence effect of Doppler shift when the parallel code phase is utilized to capture the GPS satellite signal is studied. In order to reduce the influence of picket?fence effect and improve the acquisition precision of Doppler shift， a generalized extended approximation method is proposed to improve the estimation accuracy of Doppler shift. The method is optimized while maintaining the algorithm computation amount to further reduce the impact of noise on the acquisition accuracy of Doppler shift. The simulation results verify that the method is effective.

Keywords： picket?fence effect； Doppler shift； generalized extended approximation method； GPS； satellite signal； acquisition precision

0 引 言

为了提高计算效率，通常采用FFT算法对采样信号的频谱进行计算，设数据点数为[N=Tdt=Tfs，]则计算得到的离散频率点为[X（fi）， fi=ifsN，i=0，1，2，…，N2，]这样就只能看到频谱的一部分，因此会使一部分有用的频率成分被漏掉，此种现象被称为栅栏效应。在导航信号的并行捕获中，实际的多普勒频移值不会恰好在信号的采样点上，由于栅栏效应的影响，实际的多普勒频移值会被漏过去，在对采样信号做FFT变换时就必然会产生较大误差，影响最后多普勒频移的估计值。广义延拓逼近法是一种综合了插值法和拟合法优点、具有约束条件的数值逼近方法，本文尝试将此方法应用于捕获过程中对多普勒频移的精确估计，同时在基本广义延拓逼近方法的基础上，为了进一步降低噪声对捕获精度的影响，提出一种优化的广义延拓多普勒频移估计方法，实现了对多普勒频移的精确捕获。

1 广义延拓逼近法

广义延拓逼近法由施浒立首先提出[1]，在随后的发展中得到不断完善，文献[2?5]分别将广义逼近法用于GPS导航的高程拟合、定位增强和精密星历等方面。相比于插值法和拟合法，其主要优点是在分段边界点上满足插值条件，使得分段之间的变化具有一定的协调性，另外又利用分段周围节点（包括内点）将每个分段进行延拓，实现分段最佳拟合，从而可以吸取插值法和拟合法的优点，将两者结合起来，提高数值逼近精度。

已知函数[u]的一组离散数据[uj，xjuj=u（xj），xj∈Ω，][j =1，2，…，n，]运用分片逼近的思想，将[Ω]划分为[m]个互不重叠的子区域[Ωe，]子区域有[r]个节点。在[Ω]上构造一个近似函数[U，]满足条件[U（X）=ui，i=1，2，…，n。]根据广义延拓的思想，将单元域[Ωe]进行延拓，得到延拓域[Ω′e。]设延拓域[Ω′e]内有[s]个节点，其中属于单元域[Ωe]内的有[r]个节点，且[r

[Ue（x）=j=1tkejbej（x）] （1）

式中：[be1，be2，…，bet]是[Ωe]上的一组基函数；[ke1，ke2，…，ket]为待定系数；[t]为逼近函数项数，且[r

式中：[bij=bj（xi）；η]为[r]个拉格朗日乘数法参数列向量；[k]为[t]个待定参数列向量；[u]为广义延拓域内[s]个节点的值组成的列向量；[uI]为单元域内[r]个节点值组成的列向量。

对式（4）进行矩阵求逆运算，可以解出逼近函数中的待求系数，确定单元域上的插值函数，之后在单元域内进行插值计算。对每个子区域[Ωe]均按上述方法求解，最后将各个分片函数拼接起来，就可以得到总域上的逼近函数[U（X）。]

2 基于广义延拓逼近的多普勒频移估计方法

2.1 算法思想

由对频偏进行一维搜索的精捕获可以看到，要逼近的图形接近一个抛物线，不失一般性，可以假设广义差值函数为二次型[6]：

最后得到总域的逼近函数为：

由粗捕获可以得到误差较大的多普勒频移值[fr，]然后在临近的区域[fr-500 Hz， fr+500 Hz]内选取[f0=fr-500， f1=fr-250， f2=fr， f3=fr+250， f4=fr+500，]分别设为[xi-2，xi-1，xi，xi+1，xi+2，]分别计算对应的相关值[y（xi-2），y（xi-1），y（xi），y（xi+1），y（xi+2），]如图1所示，以单元域[Ω]为例，在单元域[Ω]上的点为[xi，xi+1，]在扩展域[Ω]上的点为[xi-1，xi+2，]根据广义延拓逼近函数的定义可知，所求函数[Ui（x）]在单元域[Ω]上的延拓需要满足以下条件：

式（8）可以采用拉格朗日乘数法，即求解带条件约束的极值。

即：

2.2 算法的优化

经过精确捕获后的相关函数值与频率误差的关系是辛格函数[6]，在最大值周围的函数图形是凸函数，峰值点落在样值点的最大值和次大值点之间[7?8]。由于噪声的存在，样值点的取值一定会存在误差，如果严格通过存在误差的点，会降低结果的精度。由于只是求最大值，所以只要求在最高值点左右两个单元域内构造的函数平滑不出现断层即可。可以让求取的逼近函数[Ui（x）]只通过最大值点，这样虽然会使左右单元域和其他单元域的连接处产生断层，但最大值点左右两侧的单元域内构造的函数依然平滑，不影响对峰值点的估算，而且这种改进会降低噪声对构造函数的影响，提高峰值点的估算精度。

优化后的广义延拓进行逼近需满足如下条件：

式中[xmax]是所有样值点中[y（x）]取得最大值的频点。

3 数字仿真实验

3.1 运算量的对比分析

目前，GPS接收机中精捕获的方法最有代表性的有：加长数据FFT法和相位检测法，按照复数乘法的次数进行运算量对比[9]。

在仿真中，1 ms中采样[N=]5 000点的数据。

1） 由于之前的粗捕获已经计算过[f0=fr-500， ][f2=fr， f4=fr+500]的值，所以广义延拓逼近只需要计算[f1=fr-250， f3=fr+250]两个频点的值即可。复数乘法的次数是[2N=]10 000次。

2） 加长数据FFT法，为了达到想要的估计精度，必须将粗捕获的步长进行细化，要达到10 Hz的分辨率需要100 ms的连续数据。在1 ms中采样5 000点的数据，100 ms中包含500 000个数据点，在末尾添上24 288个0，构成[N=524 288]长的序列。所需复数乘法运算次数为[N2log2N=]4 980 736。

3） 相位检测法：该方法所需复数乘法次数为[8N=]40 000次。

三种精捕获方法的计算量见表1。

由表1可见，基于广义延拓逼近的多普勒频移估计方法的运算量比目前常用的两种方法都要少，如果以1 ms采样5 000点的数据为例，可以得到其减少比例分别为498倍和4倍，计算效率提高得非常明显。

3.2 仿真实验

由于对频偏进行一维搜索的精捕获虽然计算量很大，不适合用于真正的接收機，但是由于这种方法可以通过控制步长从而控制得到多普勒频移值的估计精度，所以将这种方法设为广义延拓插值法的对比组。对PRN#2的卫星信号进行仿真，在信噪比SNR=-20 dB的情况下，对标称[Fif=]2 MHz的中频信号进行精捕获，设置多普勒频移为4 859.3 Hz。图2为在最大样值点左右两个单元域内用广义延拓逼近法构造的函数图形。

分别对频偏一维搜索的精捕获（步长为10 Hz）、广义延拓逼近法精捕获、优化的广义延拓逼近法精捕获仿真100次，并分别计算与真实多普勒频移的误差、方差等，结果分别如图3和表2所示。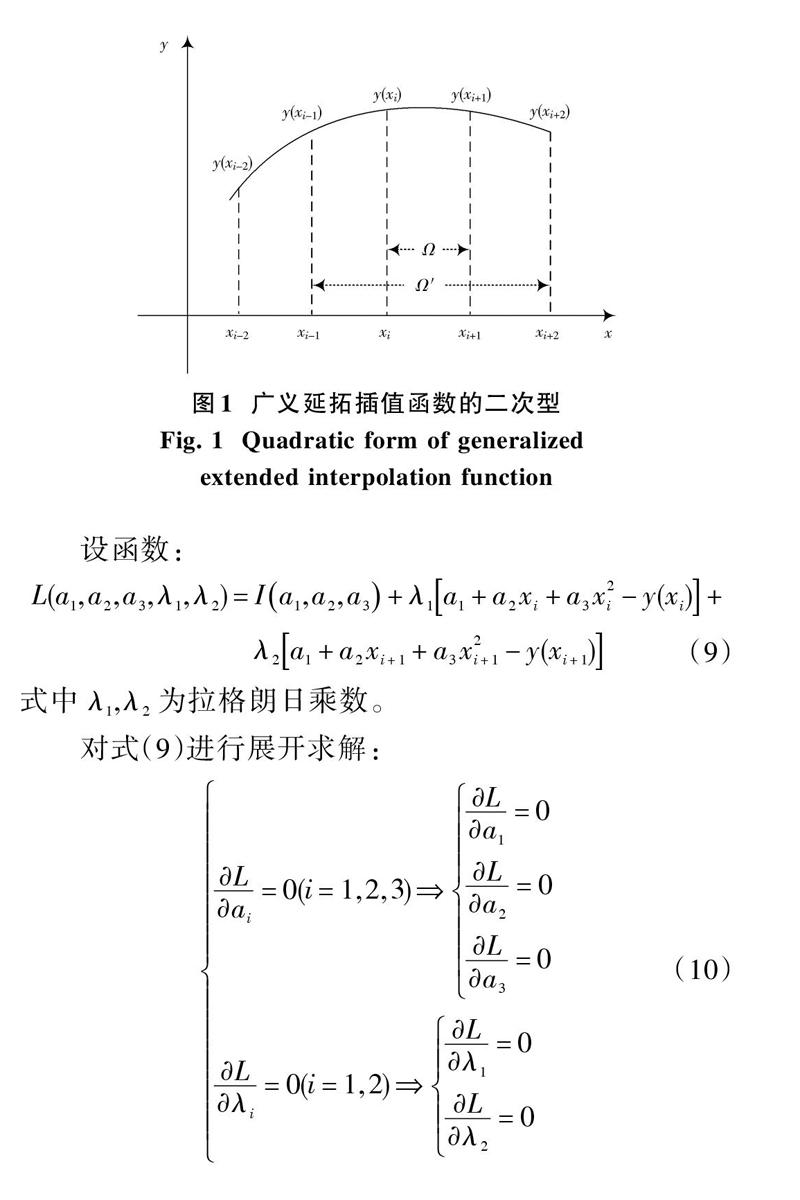

通过图3和表2可知，优化后的广义延拓逼近法误差值远低于以10 Hz为步长对频率进行一维搜索的误差值，且得到的估计频率能够使卫星信号落到跟踪环路的搜索范围内。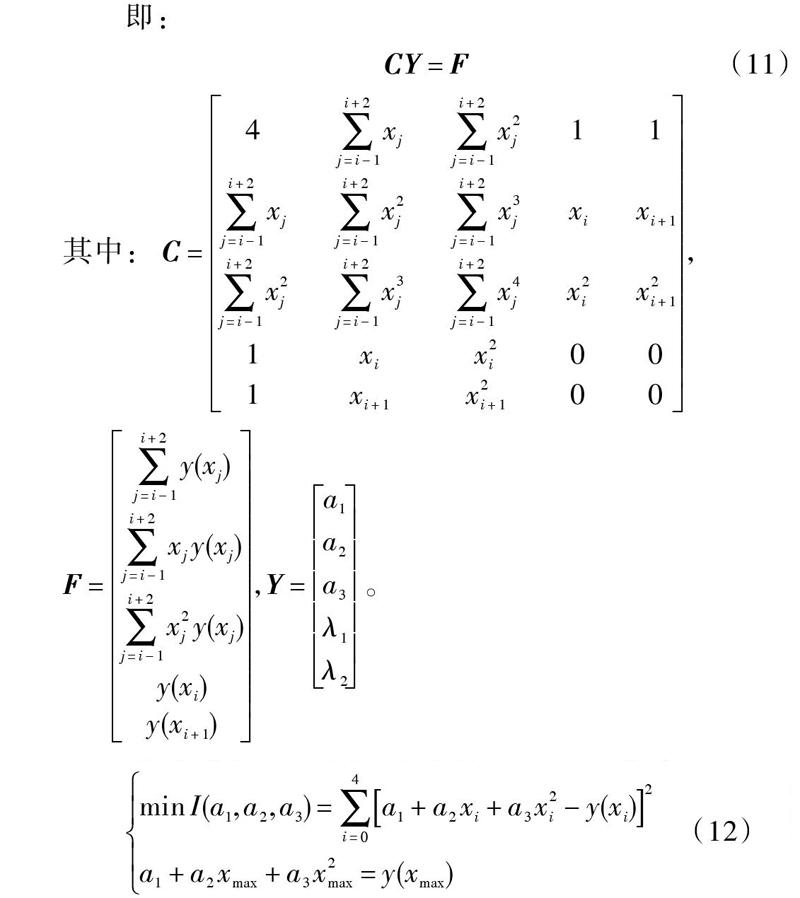

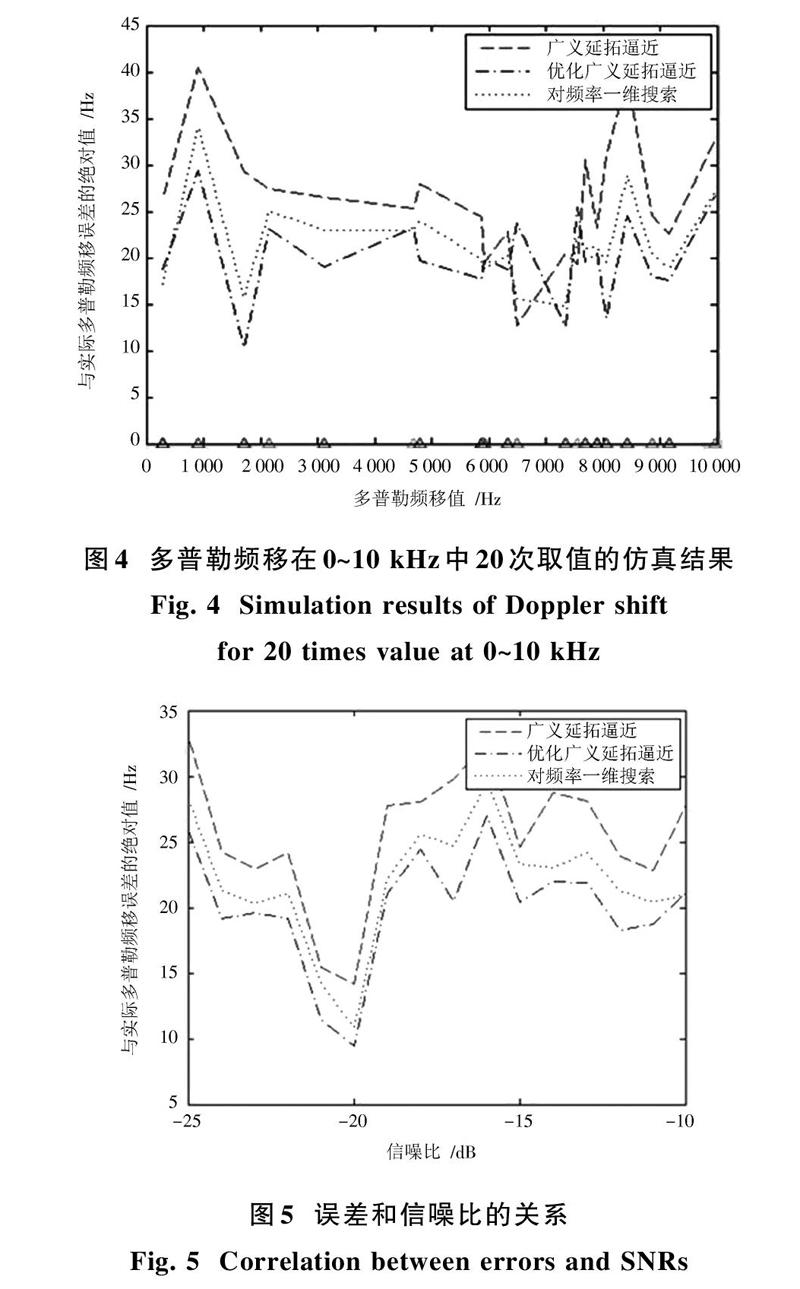
信噪比为-20 dB时，在0～10 kHz的多普勒频移中随机选取20个值，并分别对这些多普勒频移值进行100次估计，结果取与真实多普勒频移误差的绝对值的均值，其仿真结果如图4所示。信噪比从-25～-10 dB变化时，分别对上述三种精捕获方法进行100次仿真，取结果绝对值的均值，其仿真结果如图5所示。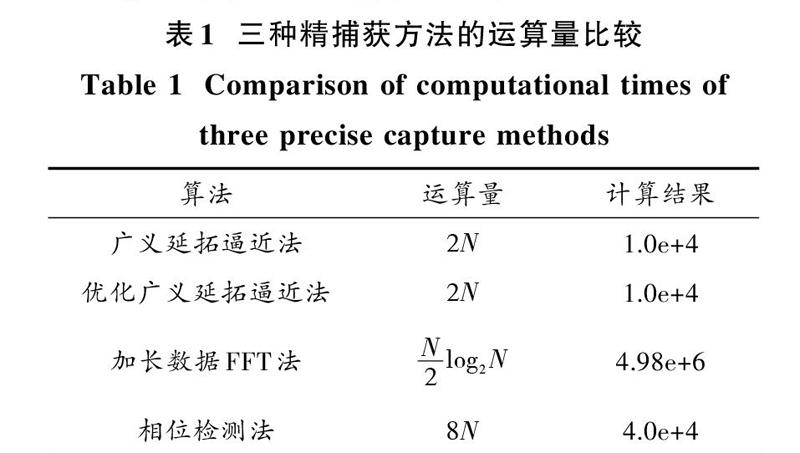

由图4和图5可以看到多普勒频移值在0～10 kHz随机变化，信噪比在-25～-10 dB随机变化时，优化后的广义延拓逼近法得到的多普勒频移估计值的误差最小。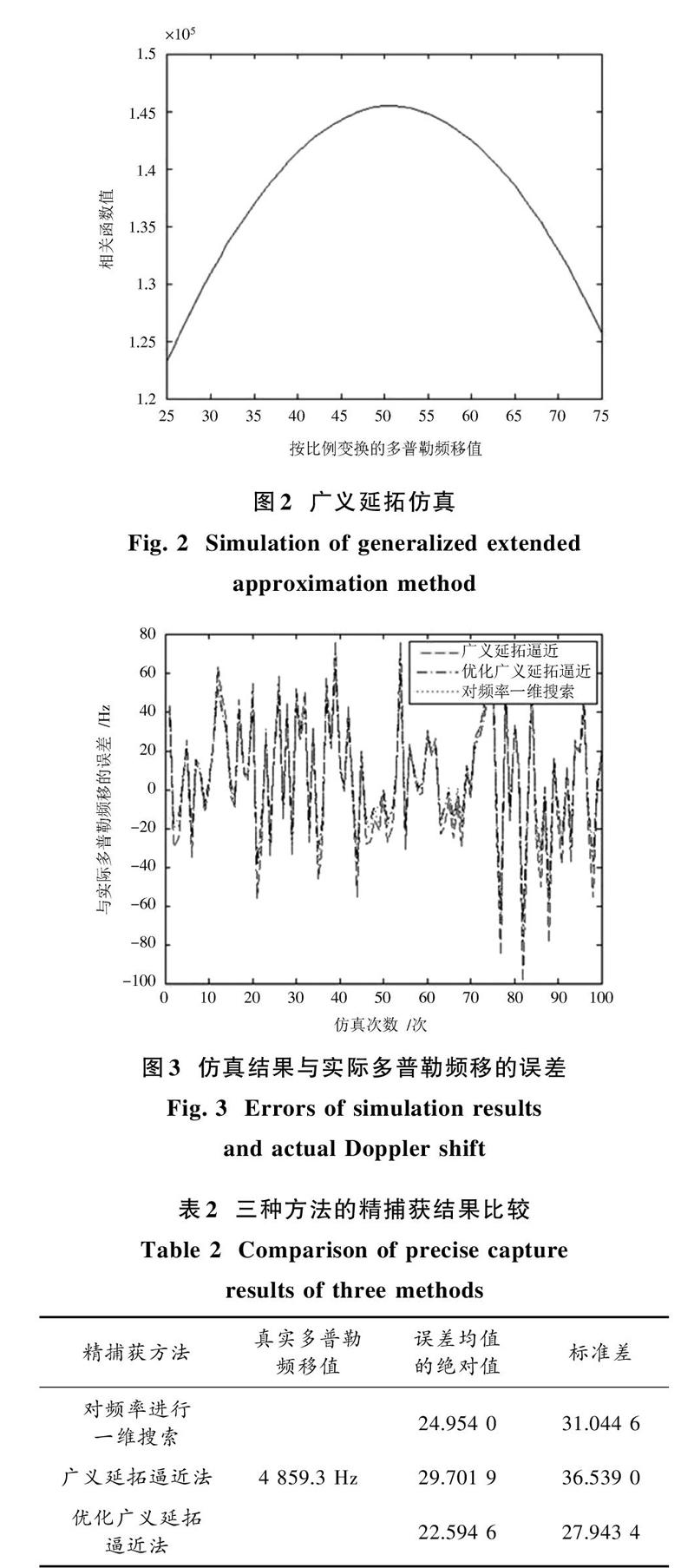

4 结 语

本文针对并行捕获多普勒频移存在的栅栏效应，采用广义延拓逼近法提高捕获的多普勒频移的精度，在不增大运算量的基础上对广义延拓逼近算法进行优化，降低了噪声对捕获精度的影响。并对优化前后的两种方法进行仿真，仿真结果证明了广义延拓逼近方法得到的估计频率能够使卫星信号落到跟踪环路的搜索范围内，而且优化后方法的抗噪声能力得到了较大的增强。

参考文献

[1] 施浒立.工程科学中的广义延拓逼近法[M].北京：科学出版社，2005.

SHI Huli. Generalized extension method in engineering science [M]. Beijing： Science Press， 2005.

[2] 林国钻，邱斌.基于广义延拓逼近法的GPS高程拟合[J].海洋测绘，2015，35（5）：35?37.

LIN Guozuan， QIU Bin. GPS elevation fitting based on genera?lized extended approximation method [J]. Hydrographic surve?ying and charting， 2015， 35（5）： 35?37.

[3] 杜晓辉，施浒立，裴军，等.广义延拓插值法在CAPS虚拟卫星定位中的应用[C]//第三届中国卫星导航学术年会电子文集—S05卫星导航增强与完好性监测.广州：中国卫星导航系统管理办公室学术交流中心，2012：130?135.

DU Xiaohui， SHI Huli， PEI Jun， et al. Application of CAPS virtual satellite positioning based on generalized extended approximation [C]// 2012 China Satellite Navigation Conference. Guangzhou： Communication Center of China Satellite Navigation System Management Office， 2012： 130?135.

[4] 刘成，施浒立，王兆瑞，等.一种基于接收机钟差广义插值法的卫星定位增强算法[J].宇航学报，2013，34（2）：186?192.

LIU Cheng， SHI Huli， WANG Zhaorui， et al. An enhanced satellite positioning algorithm based on generalized interpolation method of receiver clock error [J]. Journal of astronautics， 2013， 34（2）： 186?192.

[5] 申俊飞，郑冲，陈金春.广义延拓插值法在卫星精密星历中的应用[J].导航定位学报，2014，2（3）：55?57.

SHEN Junfei， ZHENG Chong， CHEN Jinchun. Application of generalized extended approximation method in precise epheme?ris [J]. Journal of navigation and positioning， 2014， 2（3）： 55?57.

[6] 刘长松，苟鹏飞，来逢昌，等.GPS频域相关捕获算法的Matlab/C实现[J].微电子学与计算机，2009，26（4）：193?196.

LIU Changsong， GOU Pengfei， LAI Fengchang， et al. The Matlab/C implementation of frequency domain correlation acquisition algorithm in GPS [J]. Microelectronics & computer， 2009， 26（4）： 193?196.

[7] 刘银恩.高精度频率估计算法研究[D].南京：南京理工大学，2007.

LIU Yinen. Study on high?precision frequency estimation algorithm [D]. Nanjing： NUST， 2007.

[8] 龚岳洲，周新力，孙小东，等.一种高精度的Rife算法[J].无线电工程，2013，43（2）：30?33.

GONG Yuezhou， ZHOU Xinli， SUN Xiaodong， et al. A high?precision Rife algorithm [J]. Radio engineering， 2013， 43（2）： 30?33.

[9] 曾庆喜，王庆，朱国良，等.一种GPS信号多普勒频移的精确捕获算法[J].数据采集与处理，2009，24（2）：223?226.

ZENG Qingxi， WANG Qing， ZHU Guoliang， et al. Precise acquisition algorithm for GPS signal Doppler frequency shift [J]. Journal of data acquisition & processing， 2009， 24（2）： 223?226.

[10] ZIENKIEWICZ O C， TAYLOR R L， ZHU J Z. The finite element method： its basis and fundamentals [M]. Butterworth： Heinemann， 2010.

[11] SHEPARD B D. A two dimensional interpolation function for irregularly spaced data [C]// Proceedings of 1968 the 23rd ACM National Conference. New York： ACM， 2010： 517?524.