利用AP-SSVM算法识别GIS的局放缺陷类型

高强，刘齐，张军阳，许永鹏(. 上海交通大学 电气工程系，上海　0040；.国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳　0006)

0　引　言

局部放电(Partial Discharge，PD)检测是对气体绝缘组合开关(Gas Insulated Switchgear, GIS)开展绝缘情况评估的关键方法。PD将引起绝缘老化，导致绝缘故障，严重影响使用寿命。但是GIS内部不同的缺陷类型对绝缘影响的差异性较大，因此在GIS绝缘故障诊断中，缺陷类型的识别非常关键[1-4]。

支持向量机(SVM)已在缺陷识别中得到了一定的应用。如文献[5]采用FCM聚类算法提取特征参数，再将这些特征参数输入SVM进行识别。文献[6]提出了过程功率谱信息熵SVM的故障诊断方法。文献[7]提出了小波包变换和SVM相结合的识别方法。通过小波包分解及重构进行特征提取，再带入SVM中进行准确分类。文献[8]提出了一种基于熵特征和SVM的识别新方法。首先提取局放信号的多维熵特征参数，再通过基于二叉树的SVM进行模式识别。

本文提出一种基于AP-SSVM算法的GIS缺陷类型识别方法，首先利用小波包变换对GIS局放信号进行分解，并提取时频信息熵特征；然后采用AP聚类算法对各子频带的时频信息熵特征进行聚类，实现特征参数的优化，最后将这些特征参数输入训练好的自建议支持向量机(SSVM)分类器以识别GIS的缺陷类型。

1　特征提取

1.1　小波包变换

小波变换是一种灵活的，扩展性好的时频分析方法，但是当信号在高频区分布紧密时，小波变换的分辨率难以提高。而小波包变换在每个尺度上频率带宽相同，可以保证变换不会增减原始信号的信息，还能根据被检测信号的特征，自适应地选择恰当的频带分析，所以小波包变换在中高频的处理上比小波变换的分解更精确，效果更好，非常适合处理非稳态信号[9]。以针尖缺陷的局放信号为例，小波包分解获取的各子带系数如图1所示。

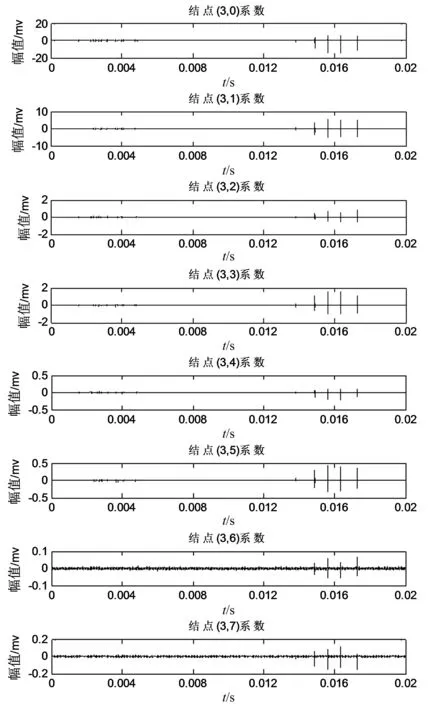
图1　小波包分解各子带系数图

1.2　AP聚类

对小波包分解后的GIS局放信号进行傅立叶变换，得到对应的频率系数，提取时域和频域信号的信息熵，并进行AP聚类[10]。AP聚类与FCM聚类等算法相比，初始约束条件较少，无需定义类的数目，在迭代的过程中会自动选择合适的聚类中心并识别出类中心的个数。

首先提取某类缺陷的50组小波包分解后子带系数的时频信息熵[11]，并进行归一化处理，再进行AP聚类，然后对分类后的子带系数进行排序，提取排名在前的若干子带系数，以及各聚类集合的minkowski距离[12]。

2　自建议支持向量机

2.1　基于先验知识的SVM

在以先验知识为基础的SVM中，测试数据的标记可根据∀x,D1x≤d1约束，其中x属于{+1}类；如果D2x≤d2那么x属于{-1}类[13]。根据经典SVM，不满足这些约束的测试数据会被标记。此外，建议可以以一种更普遍的方式表达，例如任何属于建议区域i的x，class(x)=-1；任何属于建议区域j的x，class(x)=+1，这些建议区域通常是数据输入空间中的凸多面体区域。考虑一般的建议，如Dx≤d⟹z(wx-b)≥1，其中z=+1表明x属于+1类而z=-1同样表明类别。

2.2　自建议SVM

使用专家的先验知识，有一个逐步增加的使用建议集。然而，也有一些在实际应用中的困难，比如这些知识如何以约束条件的形式表述。此外，这些方法包括新的参数，从而提高了SVM的计算成本。另一方面，集合算法是迭代的程序，增加了计算成本，却并不是总能提高SVM的性能，有时甚至会使性能下降。

本文提出了一个非迭代的方法，从训练阶段提取后续的知识。在传统的SVM方法中，测试阶段从训练阶段获取的唯一信息是第一类支持向量或超平面位置。后续的知识可以是关于第一类支持向量的深层信息，即从第二类支持向量中提取的知识。而且传统的SVM忽略了训练阶段中没有被内核线性地分开的训练数据。它会通过引入公差参数的目标函数和约束条件发生。但是，如果数据与测试集中的错误分类数据类似或相同，它将再次被错误分类，因为与错误分类数据接近的数据是不确定的。这种错误分类是不合理的，因为它是由于训练阶段可用的数据和信息被SVM算法忽略造成的。

我们首先定义错误分类的数据集MD，在训练阶段按如下形式：

(1)

在式(1)的右边，我们可以使用任何SVM决策函数和内核。MD集合可以是空的，但实验结果表明，出现错误分类的数据，在训练阶段是一种普遍现象。

对于MD中的每个xi，邻域长度(NL)定义为：

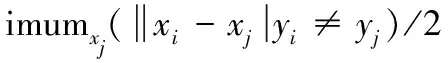
(2)

式中：xj,j=1,…,N,是不属于MD集中的训练数据。

如果训练数据通过使用映射函数被映射到一个更高的维度，那么xi和xj之间的距离可以参考相关内核k并根据下面的方程计算，

(3)

以NL的结果为基础，对测试集中的每个xk，建议权重AW(xk,j)(其中J=+1或-1)按照如下方法计算：

(4)

这些AW代表测试数据有多么接近错误分类数据。总之，自建议SVM(SSVM)步骤概括为：

(1)训练阶段

首先进行普通的SVM训练，再通过式(1)发现MD集。如果MD是空的，进入测试阶段或通过式(2)为MD的每一项计算NL。

(2)测试阶段

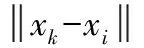
3　局放试验模型

GIS的PD试验平台示意图如图2所示。主要包括380 V/50 Hz无局放高压电源、126 kV GIS和最高采样率为20 GHz、有效带宽为2.5 GHz的示波器。

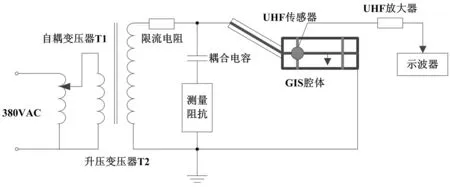
图2　GIS的PD试验平台示意图

(1)高压导体突出物模型

GIS高压导体表面上的金属突出物会导致突出物附近的局部电场畸变，引发典型的尖-板电晕放电。在正常工作电压下，该缺陷可放电稳定，可一旦有暂态过电压(雷电过电压或操作过电压)发生，则可能会引发击穿故障。模型制作示意图如图3(a)所示。

(2)悬浮电极模型

本模型通过在一圆柱形环氧树脂内放置一金属而制成。环氧树脂上表面加高压，下表面接地，模拟GIS中的悬浮电极放电。模型制作示意图如图3(b)所示。

(3)外壳底部自由金属微粒模型

自由金属微粒是导致GIS故障的最主要原因。本模型采用金属小球，放置于上下两电极之间。模型制作示意图如图3(c)所示。

(4)绝缘气隙模型

气隙放电也称为气泡放电，是绝缘子在浇注过程中受热不均而造成的一种绝缘子内常见的绝缘缺陷。本模型通过在一圆柱形环氧树脂内密封一段柱状气隙而制成。模型示意图如图3(d)所示。

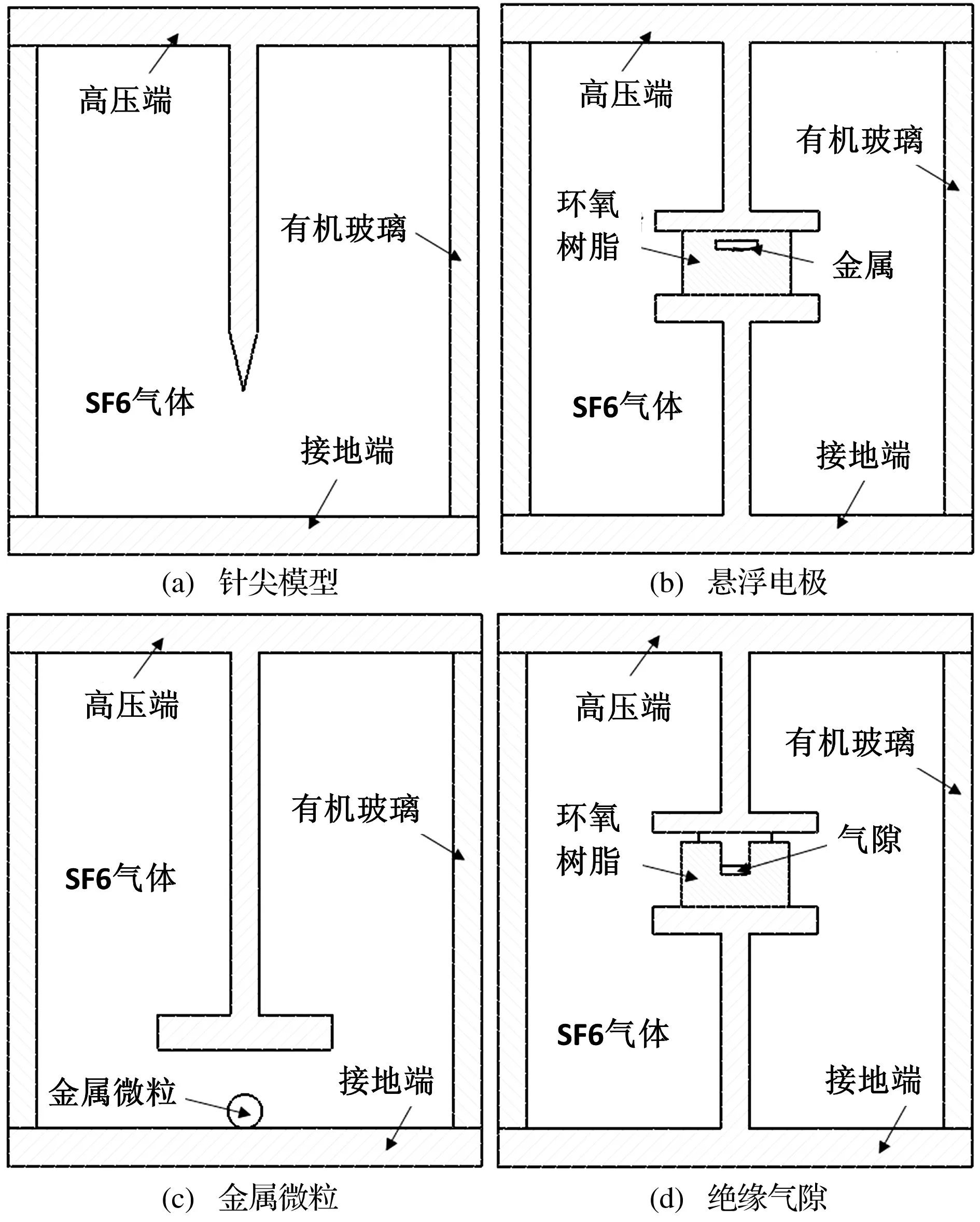
图3　四种GIS典型缺陷模型示意图

图4为高压导体突出物、悬浮电极、自由金属微粒和气隙等4种典型缺陷模型的局放UHF时域信号和频谱分析。

图4　典型缺陷模型的局放UHF信号

对上述4种缺陷模型局放UHF信号进行时域和频域分析，可以发现，对电晕放电UHF信号频谱分析可见，UHF信号频谱主要分布在350 MHz～450 MHz之间以及700 MHz～1.1 GHz之间；对悬浮放电UHF信号频谱分析可见，UHF信号频谱主要分布在350 MHz～500 MHz之间；对金属微粒放电UHF信号频谱分析可见，外置UHF信号频谱主要分布在300 MHz～500 MHz之间，与悬浮放电类似，500 MHz以下低频段分量增强，而高频段分量有所衰减；对气隙放电UHF信号频谱分析可见，外置UHF信号频谱主要分布在300 MHz～500 MHz之间。

4　信号研究

对4种缺陷类型产生的GIS局放信号进行小波包分解，并提取时频信息熵特征；然后采用AP聚类算法对各子频带的时频信息熵特征进行聚类，以AP聚类数为3为例，GIS各缺陷的局放信号的时频域聚类情况如图5所示。并计算各缺陷类型的minkowski距离，结果如表1所示。

图5　GIS缺陷典型信号的AP聚类图

将不同缺陷的GIS局放信号进行小波包分解，对各小波包系数进行时频分析，提取信号时域和频域的信息熵，经过AP聚类后，确定最优小波包系数，并将对应的信息熵分别带入SVM，AP-SVM和AP-SSVM分类器模型，进行20次独立测试，不同缺陷类型下各模型的平均识别准确率如图6所示。

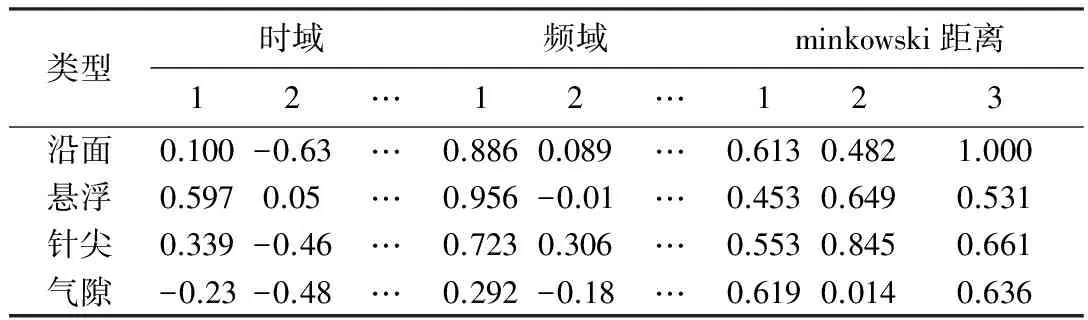
表1　不同缺陷类型的minkowski距离及时频坐标

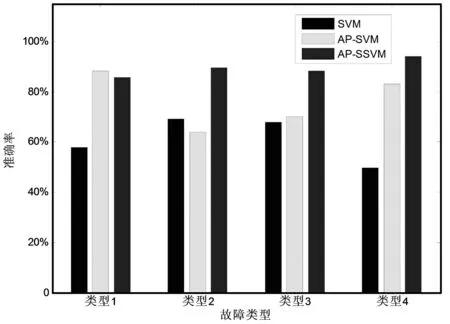
图6　不同缺陷类型下各模型的平均识别准确率

从图6中，我们可以发现，针对各种缺陷类型，AP-SSVM的平均识别率分别为85.58%，89.65%，88.17%，93.96%，在故障类型2，3，4方面，平均识别率比SVM，AP-SVM提高10.93%以上，尤其是在故障类型2方面，平均识别率提高20.41%，在故障类型1方面，虽然比AP-SVM的平均识别率低2.56%，基本属于持平状态。

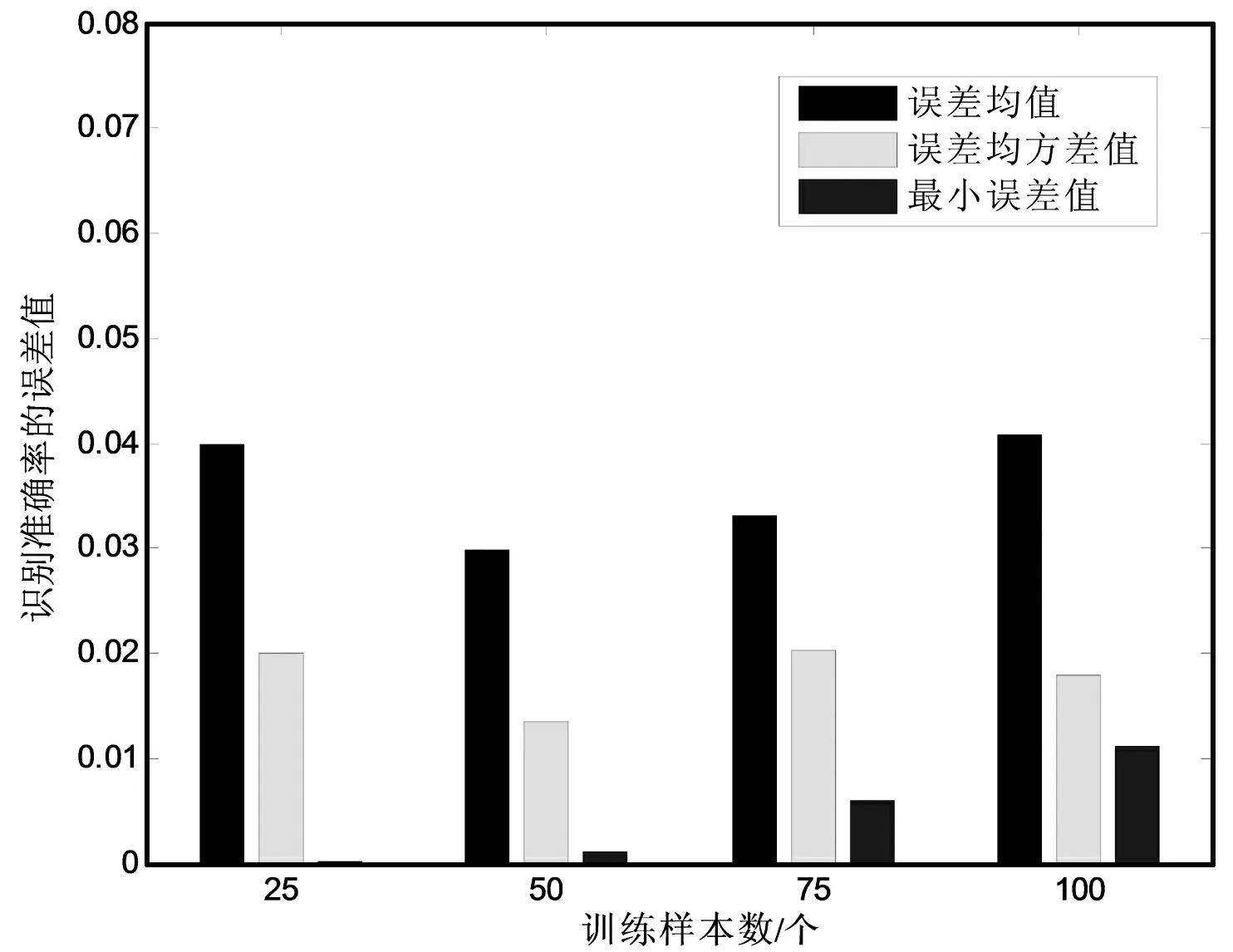
图7　不同训练样本数对应的识别准确率误差图

不同训练样本数对应的识别准确率误差均值，误差均方差，最小误差值如图7所示。可以发现，伴随训练样本数增加，最小误差值也在逐渐变大，当训练样本数为25时，最小误差值为0.000 1，而当训练样本数为100时，最小误差值为0.011 2。在误差均方差方面，当训练样本为50时，误差均方差最小为0.013 5，当训练样本为75时误差均方差最大为0.020 3，说明本文提出的AP-SSVM稳定性较好。误差均值方面，在训练样本为50时，误差均值最小为0.029 9，在训练样本为100时，误差均值最大为0.040 8。

通过各缺陷类型的平均识别准确率和不同训练样本情况下的误差情况可以发现，本文提出的AP-SSVM算法能够有效的识别GIS的缺陷类型，且识别效果稳定性强。

5　结束语

本文利用AP-SSVM算法识别GIS的缺陷类型，得到如下结论：

(1)采用小波包变换对GIS局放信号进行分解，并提取时频信息熵特征；然后采用AP聚类算法对各子频带的时频信息熵特征进行聚类，实现特征参数的优化，实验数据表明，提取的特征参数能够有效的描述GIS局放信号。

(2)通过自建议支持向量机(SSVM)分类器以识别GIS的缺陷类型，实验数据表明，识别精确度优于SVM和AP-SVM，能够达到85%以上，识别误差均值也保持在0.04以下，具有较好的实用性和推广性。

参考文献：

[ 1 ] 丁登伟, 唐诚, 高文胜, 等. GIS 中典型局部放电的频谱特征及传播特性[J]. 高电压技术, 2014, 40(10): 3243-3251.

[ 2 ] 唐炬, 曾福平, 范庆涛, 等. 基于荧光光纤检测 GIS 局部放电的多重分形谱识别[J]. 高电压技术, 2014, 40(2): 465-473.

[ 3 ] 张晓星, 舒娜, 徐晓刚, 等. 基于三维谱图混沌特征的 GIS 局部放电识别[J]. 电工技术学报, 2015, 30(1): 249-254.

[ 4 ] 律方成, 金虎, 王子建, 等. 主分量稀疏化在 GIS 局部放电特征提取中的应用[J]. 电工技术学报, 2015, 30(8): 282-288.

[ 5 ] 李庆辉, 李艾华, 苏延召, 等. 结合 FCM 聚类与 SVM 的火焰检测算法[J]. 红外与激光工程, 2014, 43(5): 1660-1666.

[ 6 ] 费成巍, 白广忱, 李晓颖. 基于过程功率谱熵 SVM 的转子振动故障诊断方法 [J]. 推进技术, 2012, 33(2): 293-298.

[ 7 ] 朱艳伟, 但扬清, 陈东海, 等. 小波包变换和支持向量机在孤岛与扰动识别中的应用[J]. 高电压技术, 2014, 40(8):2343-2347.

[ 8 ] 李一兵, 葛娟, 林云. 基于熵特征和支持向量机的调制识别方法[J]. 系统工程与电子技术, 2012, 34(8): 1691-1695.

[ 9 ] 陈伟根, 谢波, 龙震泽, 等. 基于小波包能量熵的油纸绝缘气隙放电阶段识别[J]. 中国电机工程学报, 2016, 36(2): 563-569.

[10] 周琼, 贠志皓, 丰颖, 等. 风电接入下基于 AP 聚类的无功功率—电压控制分区方法[J]. 电力系统自动化, 2016,40 (13): 19-27.

[11] 陈伟根, 谢波, 龙震泽, 等. 基于小波包能量熵的油纸绝缘气隙放电阶段识别[J]. 中国电机工程学报, 2016, 36(2): 563-569.

[12] 徐德刚, 徐戏阳, 陈晓, 等. 基于 Minkowski 距离的一致聚类改进算法及应用研究[J]. 湖南大学学报 (自然科学版), 2016, 43(4): 133-140.

[13] 贾嵘, 张欣伟, 徐其惠, 等. 基于 LS-SVM 回归的频域分析法及其在局放窄带干扰抑制中应用[J]. 电力自动化设备, 2009 (9): 50-53.