计及分布式能源影响的母线净负荷预测方法研究

黄静，陆春良，张俊，吴华华，罗欣，申鸿伟(.国网浙江省电力公司，浙江 杭州　30007； . 北京清软创新科技股份有限公司，北京　00085)

0　引　言

母线负荷预测是电力系统的一项日常基本工作,准确的预测结果对于指导电网安全经济调度具有重要意义[1]4。以母线负荷为主要研究对象的母线负荷预测技术难度较大。因为电网中母线数目众多，且各个母线负荷波动频繁、变化模式复杂、变化规律各不相同。

迄今为止已提出了多种各具特点的母线负荷预测方法，其中包括考虑了气象条件的方法[2-5]，考虑了周末与节假日效应的预测方法[6-7]，以及考虑了小水电的预测方法[8]。文献[9-12]在考虑分布式电源并网的影响的同时，分别采用了夏季和冬季典型负荷曲线比较、建立等效模型、最小二乘支持向量机和混沌理论等方法进行了相关研究。以上方法对分布式发电功率接入后的母线负荷预测方法进行初步的研究和探讨，但均为单一方法或模型的应用，未能考虑母线负荷的多样性和含分布式能源发电功率接入的母线净负荷剥离。

本文提出了一种结合了两阶段还原的母线净负荷预测和自适应预测策略的预测思路，从而考虑了分布式能源发电功率接入后对母线净负荷的影响。该预测思路可以帮助电力企业充分了解分布式能源接入对母线净负荷的影响，从而为发电计划的制订提供更为精确的理论依据。

1　母线净负荷预测思路

电力负荷是一个非线性，且与多种因素相关的动态复杂研究对象。不同负荷成份变化的相关影响因素不同且发展变化的模式也各有特点。本文采用文献[13]提出两阶段还原法，将母线净负荷分解为母线负荷需求与风电上网功率分别预测。对于母线负荷需求可利用自适应的母线短期负荷预测技术进行预测；对于风电功率，通过分析风电功率特性，利用特殊方法单独预测，然后将两部分预测结果合成并还原出母线净负荷，其思路为分解→预测→还原。该方法的总体思路如图1所示。

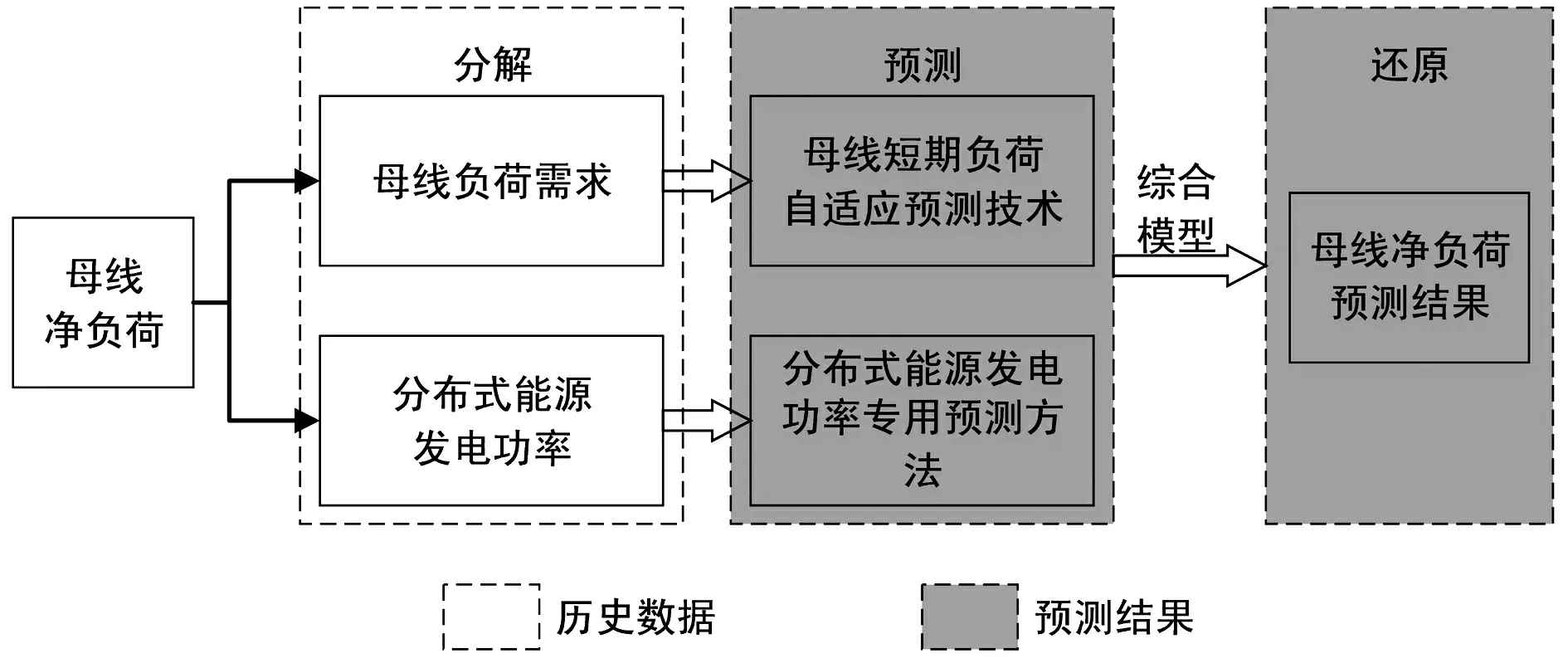
图1　两阶段还原法的总体思想

通过对母线负荷的特性进行分析，发现母线负荷体量小，不同的母线所载用户的用电类型不同时，其负荷曲线差异性很大，这是负荷产生机理的外在表现。考虑以上特点，为了能够对不同的母线负荷类型具有广泛的适用性，本文采用自适应预测技术对母线负荷进行预测。另外本文只考虑风电作为接入的分布式能源的场景，故针对风电功率时序曲线的非平稳性，本文采用ARIMA方法就其时序性和自相关性建立数学模型，对风电上网功率进行短期预测。

预测过程的具体步骤为：(1)首先根据母线净负荷与分布式能源发电功率历史数据，分解出母线负荷需求的历史数据；(2)选择合适的方法预测各种分布式能源发电功率时序曲线；(3)应用自适应预测技术预测母线负荷需求时序曲线；(4)合成以上预测结果得到该母线的净负荷，通过综合最优模型预测得到网供负荷。

图2　计算过程

2　母线负荷的自适应预测技术

该技术分为自适应训练环节和预测环节。其中，自适应训练过程是最复杂、耗时最多的环节。文献[14]中以某省220 kV母线为例，200节点的网络每次自适应训练的整体计算次数达13万余次。因此，本文采用已建成的软件平台每日凌晨进行计算来自适应得选择预测方法及各预测方法的模型参数。

2.1　自适应预测技术的抽象描述

短期母线负荷预测的精度还与预测方法和模型的选择紧密相连。目前常用的负荷预测方法有时间序列法、神经网络法、支持向量机法、组合预测方法等，短期母线负荷由于每个节点供电的用户数较少，节点负荷易受单个用户用电模式的影响较大，其负荷变化模式易变，不能用同一方法适用于所有母线，对于同一母线在不同时期也可能需要改变模型参数或更换模型来适应其趋势变化。

本文根据预测行为的时间分界特点，将时间区间作如下定义，如图3所示。

图3　预测时间序列关系图

(1)

G={i|i∈[d1,d2]}

(2)

V={i|i∈[d3,d4]}

(3)

F={i|i∈[d5,d6]}

(4)

式中：i代表日期；H代表历史区间包括历史模拟区间G和虚拟预测区间G，由历史负荷起始日d1到结束日d4所形成，包含了预测行为所需的历史样本日期；以G为已知对V的预测称为虚拟预测[1]16-17；F代表未来的预测区间，由未来负荷起始日d5到结束日d6所形成的，包含了所有待预测日期。

利用图3所示的虚拟预测原理，自适应预测过程可以抽象表达为:

(5)

(6)

2.2　自适应训练的实现过程

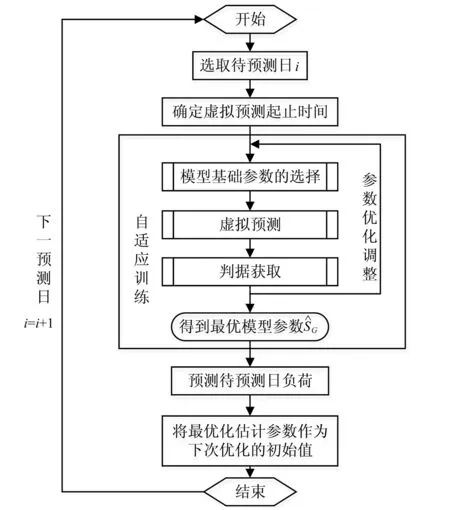
图4　自适应预测技术的逻辑框图

3　基于ARIMA的风电功率预测方法

文献[15]146对风电机组的输出功率时序曲线进行了自相关和偏相关分析，从分析结果可以看出，各被测风电机组的输出功率时序曲线均为非平稳时间序列，并且在进行了二阶差分处理后变为平稳时间序列。文献[15]148是从一个58台风电机组的风电场中抽选4台风机的输出功率时序曲线进行分析。本文选择某总装机为97.5 MW的风电场为例进行分析，该风电场包含33台1.5 MW风机和24台2.0 MW风机，对其中17台1.5 MW风机和12台2.0 MW机组的输出功率时序曲线进行自相关和偏相关分析，经过N阶差分处理后得出结论均能与文献[15]153相同，说明风电机组输出功率时序曲线若为非平稳时间序列，在经过N阶差分后可变为平稳时间序列的特征具有一定的代表性。故本文采用累积式自回归-移动平均模型对风电功率时序曲线进行预测。

对于非平稳性时间序列，Box-Jenkins预测方法的模型为累积式自回归-移动平均模型( Auto-RegressiveIntegrated Moving Average Model，ARIMA) 。考虑到风力发电上网功率的非平稳性[15]147，本文应用ARIMA模型对其进行预测，预测过程如图5所示。

图5　ARIMA预测流程

ARMA(p,q)的模型结构如下：

(7)

式中：xt为随机变量;p为自回归模型阶数;q为移动平均模型阶数;φ1，φ2，…φp为自回归系数;θ1，θ2，…θq为移动平均系数;εt为随机干扰项。应用AIC准则进行模型定阶，选择p、q值[16]。

4　实例分析

4.1　实例介绍

本文以省含风电接入的某220 kV变电站2#变压器高压侧的母线净负荷为测算实例来进行预测，该风电场的开机总容量为97.5 MW。预测时间段选择为风资源较丰富的春季一整周的时间进行预测，具体日期为2015年4月13日至2015年4月19日。风电场的开机总容量为97.5 MW，风力发电功率转入比例为100%。采用北京清软创新科技股份有限公司的母线负荷预测系统中的自适应预测技术结合本文风电功率预测算法结果，应用两阶段还原的思想对计及风力发电影响的母线净负荷进行了预测。

历史母线负荷选择预测日前三个星期的历史母线负荷需求数据，并重点考虑同类型日的历史数据，在虚拟预测时将同类型日的历史数据置前并根据训练结果给予较大权重。本文风电功率预测则也选择了前三个星期的历史数据，从而对未来日96点的母线净负荷进行预测。

4.2　考核指标

在预测结果考核指标的选择上，本文针对母线分别采用了国网同业对标中所应用的引用误差(%)、日母线负荷预测准确率(%)和日母线负荷预测合格率(%)；针对风功率分别采用均方根误差(RMSE)、平均绝对误差(MAE)、相关性系数(r)和最大预测误差(δmax)。需要特别说明的是，在最基本的引用误差计算中，负荷基准值本文采用同状态估计误差统计中的功率基准值，220 kV电压等级对应的负荷基准值为305 MVA。

4.3　结果分析

本文采用对应的省某 220 kV 变电站的历史数据，对2015年4月13日开始的一周进行母线净负荷预测。通过考核指标对母线预测结果进行统计分析，得到的母线净负荷预测准确率和合格率如表1所示。

表1　母线净负荷预测准确率和合格率

表1的统计结果来自母线净负荷预测的引用误差的计算结果，引用误差随时间的分布情况如图6所示。2015年4月17日的预测准确率在该周内最低。从图6可以看出，只有25个时刻的预测误差均小于5%，所以其合格率也较低，具体原因在结合风电功率预测结果分析后作进一步说明。

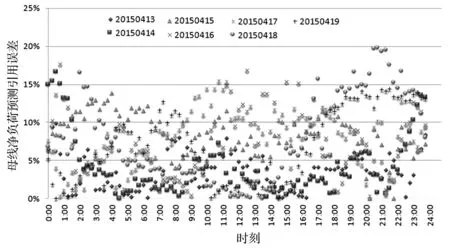
图6　母线净负荷预测引用误差分布

通过4.2节介绍的考核指标对风功率预测结果进行统计分析，得到表2。

表2　风功率预测考核指标统计结果

从表2的数据中可以看出，2015年4月15日、16日、18日和19日的风功率预测均方根误差较大，但结合表2的统计结果发现，应用本文预测方法进行的母线净负荷预测结果并未受到很大影响，即在风功率预测结果较为不理想的情况下，仍然能够对母线净负荷进行较为精确的预测，证明了本文方法的鲁棒性及其应对风电上网功率不确定性的能力。

另对2015年4月17日的实际值和预测值进行对比发现，预测各个时刻的母线净负荷均比实际值低，这是由于在风功率预测结果较好的情况下，母线负荷需求的预测结果比实际低造成的。针对以上情况调整自适应训练的启动时间，每日凌晨0:00开始对母线负荷预测算法库进行自适应训练，及时根据最新的历史负荷发生值更新算法参数后，再对未来日进行预测，预测结果准确率会有一定幅度的提升，母线净负荷预测准确率提升为91.27%，合格率提升为26.04%。

5　结束语

从本文的分析可以看出，风电等分布式能源的发电功率接入母线后对母线净负荷产生了很大的影响。本文基于以上分析提出了一种基于两阶段还原的母线净负荷预测方法。从而实现对于较为稳定的母线负荷需求采用自适应预测策略进行精确预测，并且同时结合了分布式能源发电功率预测结果。实例验证结果证明，本文方法应用于含有风电接入的母线负荷预测，在一定程度上提高了母线净负荷的预测结果。下一步可以考虑其他形式分布式能源接入对母线净负荷的影响。对于风电接入的情况，还可以考虑应用气象情况和地理信息的风功率预测方法和更长时间的历史数据进行训练，通过提高风功率预测的准确率来进一步提高母线净负荷预测的准确率。

参考文献：

[ 1 ] 康重庆,夏清,刘梅.电力系统负荷预测[M].北京:中国电力出版社,2007.

[ 2 ] 康重庆,周安石,王鹏,等.短期负荷预测中实时气象因素的影响分析及其处理策略[J].电网技术,2006,30(7):5-10.

[ 3 ] 朱陶业,李应求,张颖,等.提高时间序列气象适应性的短期电力负荷预测算法[J].中国电机工程学报,2006,26(23):14-19.

[ 4 ] 张凯,姚建刚,李伟,等.基于功率谱分解和实时气象因素的短期负荷预测[J].电网技术,2007,31(23):47-51.

[ 5 ] 赵德应,李胜洪,张巧霞.气温变化对用电负荷和电网运行的影响初步探讨[J].电网技术,2000,24(1):55-58.

[ 6 ] 刘敦楠,何光宇,范旻,等.数据挖掘与非正常日的负荷预测[J].电力系统自动化,2004,28(3):53-57.

[ 7 ] 刘皓明,余昆,梁进国,等.特殊节假日的短期负荷预测新方法[J].电力需求侧管理,2006,8(5):14-16.

[ 8 ] 金义雄,段建民,杨俊强,等.含有山区小水电负荷的气象回归短期负荷预测技术[J].继电器,2007,35(14):54-58, 69.

[ 9 ] 赵海洲. 分布式电源并网对电网负荷预测的影响[J]. 设备管理与维修, 2015,36(S1):32-33.

[10] 马亚辉.含分布式电源的综合负荷建模方法研究[D].湖南:湖南大学,2013.

[11] 颜宏文,李欣然.基于差分进化的含分布式电源母线净负荷预测[J].电网技术,2013,37(6):1602-1606.

[12] 刘熙哲.基于混沌理论的含分布式电源系统负荷预测研究[D].长沙:长沙理工大学, 2011.

[13] 徐玮,罗欣.用于小水电地区负荷预测的两阶段还原法[J].电网技术,2009,33(8):87-92.

[14] 赵燃，陈新宇.母线负荷预测中的自适应预测技术及其实现[J].电网技术,2009,33(19):55-59.

[15] 惠小健,王震.基于ARMA的风电功率预测[J],现代电子技术,2016,39(7):145-148.

[16] 李婧娇,戴长春,王正风,等.基于规律性分析的超短期负荷预测方法研究[J].计算机仿真,2014,31(7):136-139.