基于多机组并联的10 kV电网有源滤波器扩容方法
王玲,代东旭,马志骐,陈超楠,孙文(.国网辽宁省电力公司本溪供电公司,辽宁 本溪 7000; .河海大学 电气工程学院,江苏 南京 0000)
0 引 言
供电电能质量的问题近些年来越来越引起人们的重视[1]。一方面随着我国配电网中各种变流器设备、变频调速装置、电弧炉以及电气化铁路等以非线性、冲击性和不平衡为特征的新型负载的不断增加,造成电网中无功电流大量远距离传输、电压电流崎变严重、三相系统明显不平衡,甚至引起电压的波动和闪变[2-4]。另一方面,伴随现代工业自动化生产和计算机技术的快速发展,各种新型用电设备对电能质量愈加敏感[5-6]。不仅低劣的供电质量会导致产品质量降低,而且供电的中断所造成的经济损失也十分巨大。因此,如何进一步提高电能质量已成为当前迫切需要解决的重要问题。有源滤波器[7-8](Active Power Filter,简称APF)正是在上述背景下被提出的,然而,受限于电力电子器件单体容量限制,单机APF无法满足10 kV输电网络大容量补偿需求。
本文提出一种基于多机并联技术的10 kV电网有源滤波器扩容方法,考虑到10 kV电网负载侧特有的中压、大电流特性,采取变流器并联技术实现APF装置容量提升。建模可知,并联APF电路模型中存在低频环流通路,从而影响并联APF控制系统电流内环运行特性,为此采取零序电压修正方式实现并联APF环流限制。最后,10 kV/1 MW工程样机对APF并联补偿技术进行可行性验证,装置投入后10 kV网侧电流总畸变率降低为3.1%,且谐波分量均集中在两倍开关频率及其倍频段。
1 单机组APF系统等效建模
图1(a)所示为多机组并联APF系统结构图,图中APF通过10 kV/660 V降压变压器连接公共接入点(PCC),k组逆变器共用直流滤波电容C。APF基本思路是在PCC处注入与谐波电流相位一致、幅值反向的补偿电流,以保住电网输入端电流低畸变率。图1(b)中给出了单组逆变器单元理想开关模型,图中p、n分别为直流侧正、负母线。功率器件的开关函数定义如下:

图1 多机组并联APF系统原理
(1)
以直流母线的n端为参考点,根据基尔霍夫电压、电流定律建立三相变换器的开关函数模型为:
idc=[sasbsc][iaibic]T
(2)
[uaubuc]T=[sasbsc]〗Tudc
(3)
(4)
式中:udc、idc分别为直流侧的电压、电流;L为APF交流侧的滤波电感;ua、ub、uc分别为APF交流侧a、b、c相电压;ia、ib、ic分别为APF交流侧a、b、c相电流;sa、sb、sc分别为变换器a、b、c相的开关函数;uan、ubn、ucn分别为电网a、b、c相电压;uno为逆变器p端相对于三相电网0点的参考点的电压。
2 多机组APF系统环流特性分析

图2 多机组并联APF系统环流原理
图2所示为多机组并联APF系统环流分析示意图,为了便于分析并联APF系统环流流通路径,定义Ckj为第j逆变器第k相的环流。至此,可将k组APF单元的a相环流表示为:
(5)
同理,将a相环流表达式推广至bc相,可得abc三相k组单元环流表达式为:
(6)
式中:d1k、d2k、d3k分别为PWM调制主、次、零矢量占空比。
分析式(6)可知,直流母线电压udc和交流电压eabc为环流主要激励源。此外,由于采取不同的并联控制策略和PWM调制方法,使得k组APF单元出现不同的PWM开关状态,从而造成并联系统出现多组环流通路。在各PWM整流单元阻抗一致的情况下,环流大小将仅与各PWM整流器单元占空比有关,与其他因素均无关系。
3 载波移相系统环流抑制方法
为了提升APF系统对于高频谐波电流的补偿能力,需要采取较高的PWM开关频率以提升电流内环带宽。然而,考虑到开关器件的开关损耗特性,需对单组APF单元最大PWM开关频率加以限制。基于上述原因,采取载波移相PWM调制方式实现等效开关频率提升。图3中以两机组APF并联为例,给出了载波移相PWM工作原理。由图3可知,虽然两机组APF调制信号m*相同,由于三角载波互差180°,对应的PWM1、PWM2信号存在一定的差异。该差异将造成两组APF电流纹波脉动时刻移位,最终实现双机组APF网侧电流纹波脉动频率提升。
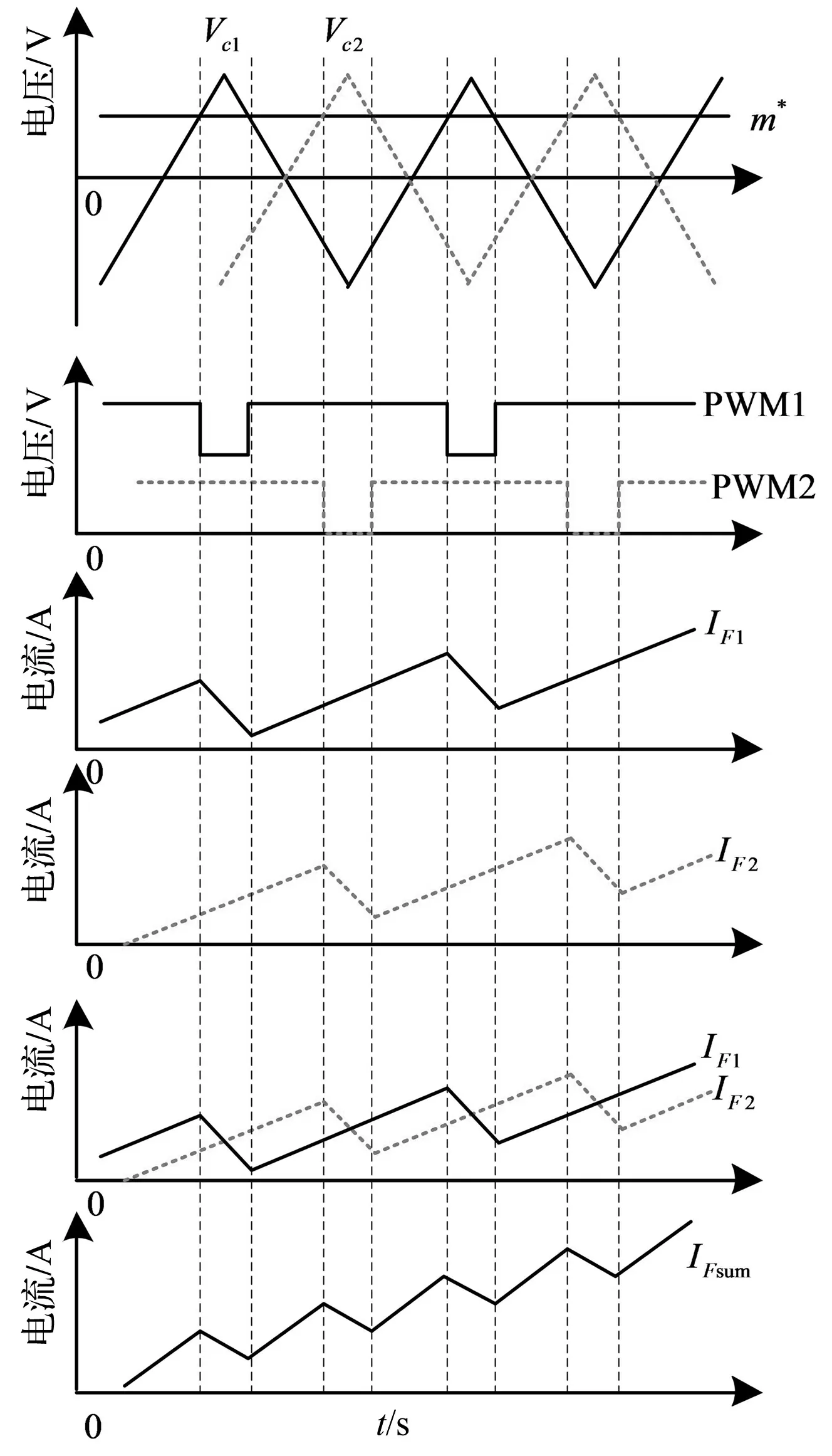
图3 载波移相PWM工作原理
从APF机组零序电流的数学模型式(6)可以看出,零序电流的变化率由两个APF机组的零序占空比之差决定。并网逆变系统中通常采用的SPWM方式,采用非零矢量Vi(i=1,2,…,6)和零矢量Vi(i=0,7)来合成控制矢量,如图4所示。设非零矢量的占空比分别为d1、d2,零矢量占空比为d0,则:
d0=1-d1-d2
(7)

图4 零矢量占空比修正原理
在七段式SPWM调制方式中通常对零矢量的作用时间t0、t7进行等值分配,引入环流控制变量y后,将零矢量V7的时间修正为(d0/2-2y)T,零矢量V0的时间修正为(d0/2+2y)T,其中变量y满足:
(8)
此时,零矢量V0、V7占空比的取值范围均为[0,d0],且满足两者之和为d0。当2个变换器的给定电流相等时,电流调节器输出的电压给定值基本相等,即逆变器1、2单元的非零矢量占空比等效,零序电流在dqz旋转坐标系下的数学模型简化为:
(9)
式(9)表明,APF并联系统z轴与dq轴完全解耦,且为一阶惯性环节,因此可选用PI调节器作为零序环流调节器。图5所示为多机组APF并联系统控制框图。
4 实验验证
为验证所提多机组APF并联系统的可行性和有效性,搭建了图6所示的双100 kW并联APF系统测试平台,图中两机组分别为APF1和APF2,测试平台谐波源以二极管整流单元进行模拟。
首先,为验证APF对于电网谐波补偿能力,图7中给出了APF补偿前后网侧电流测试结果。首先,从图7(a)中电流补偿前二极管整流桥a相电流iah可知,其呈典型的6脉动特性。在图7(b)中iah频谱分析结果中,iah总畸变率达到23.4%,且低频谐波分量含量较大,且多集中在6倍、12倍频段;图7(a)中APF系统a相给定电流iaf,iaf通过APF系统注入电网后,网侧电流ia呈标准正弦波形态,在图7(c)中ia频谱分析结果中,ia低频谐波分量得到了有效抑制,其总畸变率仅为3.1%,且多分布于30倍频以上的高频段。由此可见,APF系统对于优化网侧电流品质具有积极意义。

图6 双100 kW并联APF系统测试平台

图7 APF补偿前后网侧电流测试结果
其次,为验证双100 kW并联APF系统均流效果,图8中给出了采取环流抑制方法前、后APF系统测试结果。图8(a)中为无环流抑制环节,ia1、ia2出现一定的幅值偏差,最大达到100 A。此时,APF1机组,存在过电流风险。图8(b)中为有环流抑制环节,此时APF1和APF2注入的a相电流幅值、相位均一致,其最大电流误差仅为20 A,可见文中提及的修正零序电压环流抑制方法的可行性。图8(c)中给出了并联前端口线电压uab1、uab2及并联后端口线电压uab,并联前uab1、uab2均呈现3阶梯PWM特性。采取PWM载波移相后,相位差使得线电压uab阶梯数增多,更多的阶梯数下PWM波形品质明显提升,进一步说明了SPWM载波移相技术对于提升APF系统等效开关频率的积极性。

图8 环流抑制单元投入前、后运行结果
5 结束语
本文提出了一种基于多机并联技术的10 kV电网谐波抑制方法,并双100 kW并联APF系统测试平台对所提方法进行性能验证,可以得出以下结论:
(1)将并联载波移相PWM技术应用于多机APF系统中,可有效提升系统等效开关频率,保证并网逆变系统电网接入端口的电流品质;
(2)零矢量占空比调节法在无需改变电路拓扑的前提下,可有效降低并联逆变系统中的零序环流,保证了多机APF并联系统安全、稳定运行。
参考文献:
[1] 国家电网公司促进新能源发展白皮书(2016)[J]. 国家电网报,2016,11(6):58-62.
[2] 刘振亚. 构建全球能源互联网推动能源清洁绿色发展[J]. 华北电业, 2015,30(6):4-7.
[3] ALFONSO GIL J C, PEREZ E,ARINO C, et al. Optimization algorithm for selective compensation in a shunt active power filter[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6):3351-3361.
[4] 张雪珍,王少杰,王文华. 一种新型谐波电流双闭环控制策略[J]. 电气自动化,2016,38(4):24-26.
[6] 国网江苏省电力公司. 统一潮流控制器工程实践:南京西环网统一潮流控制器示范工程[M]. 北京:中国电力出版社, 2015.
[7] 党存禄,张艳超,周明星. 注入式混合型有源电力滤波器谐波检测方法研究[J]. 电气自动化,2012,34(1):90-93.
[8] 任磊, 姜齐荣, 魏应冬. 有源滤波器对电压源型非线性负荷稳定性分析[J]. 电力电子技术, 2016, 50(10):52-56.

