基于改进HHT算法的GIS机械振动信号时频分析

郑浩， 朱胜龙， 欧阳昱， 李檀(. 安徽省电力公司，安徽 合肥　300；. 山东大学 电气工程学院，山东 济南　5006)

0　引　言

气体绝缘金属封闭开关设备(Gas Insulated Switchgear，GIS)会产生多种机械缺陷，例如螺丝松动、断路器操作机构失灵、互感器振荡等。因此通过监测机械故障来诊断GIS内部早期缺陷能够提高GIS的运行稳定性。GIS内部故障产生的振动信号通过介质传递至GIS筒体，对于运行中的GIS设备，常在筒体表面放置传感器，接受传递过来的振动信号，从而检测GIS是否运行异常，即发生故障。由于振动信号检测法抗干扰能力强，并且与电网中广泛使用的超高频检测法可以形成互补，用来检测中低频信号，方便可靠。

但是，现阶段对于GIS的故障研究仍多集中于局部放电[1]方向，采集的振动信号也多为频率较高的电磁波信号，对存在更广泛的、频率较低的机械故障信号研究较少。由于GIS结构的复杂性，对现场运行中的GIS的振动特性[2-5]更少研究，文献[2]40中，徐天乐等人对运行中的GIS的振动信号进行了实测，但数据获取困难且数据量有限，未能分析出GIS具体的故障问题。文献[3]17中，程林等人对正常和异常的混合型高压开关设备(Hybrid Gas Insulated Switchgear, HGIS)振动信号进行多次检测处理，并从统计角度得出对应振动幅值和次数关于频率的相关图，但并没有指明故障问题。

常用的处理振动信号时频的方法是希尔伯特黄变换(Hilbert-Huang Transformation, HHT)算法，即对经过经验模态分解(Empirical Mode Decomposition， EMD)算法预处理后得到的信号进行希尔伯特变换(Hilbert Transformation, HT)处理，但经验模态分解作为一个成熟的分析时频信号的方法，仍然存在不少问题，其中比较严重的就是易产生虚假分量和模态混叠现象。具体表现在：(1)一个单独的本征模态函数(Intrinsic Mode Function，IMF)中含有全异尺度；(2)相同尺度出现在不同的IMF中。因此本文提出基于改进的HHT算法理论振动信号时频分析方法，即将总体集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)算法用于信号的预处理。

本文对GIS设备表面的振动信号进行测量，并构造螺丝松动和基于绕组变形的互感器振荡两种常见的GIS机械故障，多次检测三种工况(正常信号、螺丝松动、互感器振荡)下的GIS振动信号，引入改进的HHT方法来处理GIS机械振动信号，对三种振动信号进行时频分析，以使该种针对非线性非平稳信号的处理方法能够更广泛更深入地应用于振动信号处理领域。

1　EMD和EEMD的原理

1.1　经验模态分解[6-8]

经验模态分解方法是将复杂的信号分解成若干IMF，从而使通过HT获得的瞬时频率能够应用到实际中。IMF须满足以下两个条件，即：① 整个数据段内，极值点和过零点的个数应当相等或最多相差1；② 在任何一点，局部极大值点形成的上包络线和局部极小值点形成的下包络线的均值为零，即信号关于时间轴局部对称。具体的处理方法是：

首先根据原始信号函数s(t)的极大点和极小点求出其上包络v1(t)及下包络v2(t)的平均值:

(1)

然后求出s(t)与m的差值h，即:

s(t)-m=h

(2)

再将h看作新的s(t)重复以上操作，进行迭代，直至h满足IMF条件时，此时记作:

c1=h

(3)

将c1看作一个新的IMF，作:

s(t)-c1=r

(4)

将r看作新的s(t)，重复以上过程，依次得到c2，c3，c4…，直到r(t)基本呈单调趋势或|r(t)|很小可视为测量误差时即可停止。此时，

(5)

即将原信号分解成了n个IMF,分别是c1，c2，c3，c4…，cn，和一个剩余分量r。

经验模态分解仍然存在不少问题，其中比较严重的就是易产生虚假分量和模态混叠。因此，在EMD算法的基础上，提出了EEMD算法。

1.2　总体平均经验模态分解

针对EMD所出现的问题，EMD的提出者通过对EMD分解的白噪声结果统计特性的大量研究[9]，发现除一阶分量外，每阶IMF的功率谱都呈现相同的带通特性，而且前一阶IMF的平均频率近似为后一阶的2倍；同时还发现信号会出现频率混叠现象。基于上述分析，提出了将白噪声加入到分解信号中补充一些缺失的尺度，从而提出了总体平均经验模态分解思路。

因此，EEMD主要算法结构与EMD算法基本相同：将原始信号筛分成固有模态函数，由于筛分过程中出现了模态混叠现象，因此在筛分过程中给信号添加一个高斯白噪声信号w(t)，为每次EMD分解后剩余分量的时域分布提供一致的参考结构。

1.3　总体平均经验模态分解具体步骤

(1)通过给原始信号x(t)叠加一组高斯白噪声信号w(t)获得一个总体信号：

X(t)=x(t)+w(t)

(6)

(2)对X(t)进行EMD分解，得到各阶IMF分量：

(7)

(3)给原始信号加入不同的白噪声wi(t)，重复步骤(1)和(2)。

(8)

(4)利用高斯白噪声频谱零均值原理，消除高斯白噪声作为时域分布参考结构带来的影响，此时IMF分量Cn(t)可表示为:

(9)

EEMD所加的高斯白噪声次数服从式(10)

(10)

式中:ε为高斯白噪声的幅值；N为总体个数；εn表示原始信号与各阶的IMF相加后之间的误差。为了保证谐波检测算法的快速性，一般选取ε为0.01，N=200。

(5)因此，最后原始信号x(t)可分解为:

(11)

2　改进的HHT算法基本原理

2.1　Hilbert变换

对每个经过EEMD得到的IMF做Hilbert变换，

xi(t)=Ci(t)

(12)

(13)

得到解析信号，

z(t)=xi(t)+iyi(t)=a(t)eiθ(t)

(14)

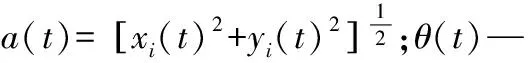
瞬时频率按下式计算

(15)

2.2　Hilbert谱

对每个IMF做HT得到:

(16)

此时忽略了残余项，上式称为Hilbert谱，记作

(17)

进一步定义边际谱

(18)

边际谱能够从统计意义上表征整组数据各个频率点的积累幅值分布。

3　GIS振动信号检测试验平台

本文试验利用某开关厂整套的110 kV单相分箱GIS设备。在GIS断路器操动机构与隔离开关连接螺丝和互感器处设置异常振动源，包括螺丝松动和基于绕组变形的互感器振荡。试验实物及故障设置位置如图1所示(故障1为螺丝松动，故障2为互感器绕组变形)。利用外置的压电式加速度传感器在GIS窥视孔下侧检测三类振动信号(正常，螺丝松动，互感器振荡)，振动测试平台如图2所示。

图1　试验平台实物图及故障设置点

图2　振动测试平台

4　基于改进HHT算法的GIS振动信号分析

4.1　时域图分析

图3(a)、(b)、(c)分别为示波器在GIS正常、故障1、故障2时采集的振动信号时域图，从时域图来看，螺丝松动和互感器振荡两种工况下的振动信号幅值均大于正常振动信号，并且螺丝松动故障下，振动信号幅值增幅明显。直观上看，互感器振荡下的振动信号密集程度最高，推测有倍频信号叠加。

图3　三种工况下的GIS振动信号时域图

4.2　平均经验模态分解(EEMD)

三组振动信号经过简单去噪处理后，通过上文的EEMD分解得到三种工况(如图4所示)下GIS振动信号的本征模函数组，各图自上而下依次为各个本征模函数(imf)和残余分量(res.)。本征模态分量相应包含了从高到低不同频率段的成分，并且随原始信号的变化而变化。

图4　振动信号EEMD分解

4.3　希尔伯特谱分解和HHT边际谱分析

通过希尔伯特变换后可以得到希尔伯特黄谱和边际谱。通过边际谱可以更直观的看出幅值随频率分布的变化。与正常运行下的振动信号的HHT边际谱(图5a)相比，故障1(图5b)和故障2(图5c)下GIS振动信号的HHT边际谱中可以非常清晰地看到故障特征，螺丝松动故障在基频100 Hz处存在振荡现象，并且幅值明显高于正常运行时的幅值，互感器振荡信号的能量主要集中于140 Hz～160 Hz和440 Hz～460 Hz范围，其幅值远高于正常运行下基频100 Hz左右的幅值。综合希尔伯特黄谱分析，可以得出两种故障的特征判据。

图5　振动信号边际谱

5　结束语

本文应用改进的HHT分析方法分析处理GIS设备振动信号。利用HHT方法，在实验室内，通过对GIS设备设置两种常见的机械故障(即螺丝松动和互感器振荡)，运用该方法对GIS设备三种工况(正常、故障1、故障2)下振动信号进行分析研究。得出以下结论：

(1)基于EEMD的时域分析，得到本征模函数组，可以获得振动信号的各成分幅值和相位情况，避免了虚假分量和模态混叠现象的出现，使得结果更加准确。

(2)基于改进的HHT分析，可得到三种工况振动信号幅值和频率的分析，得到不同故障下振动信号的特征判据。

(3)正常振动信号的频谱分布在100 Hz附近，频带较窄；螺丝松动故障振动信号的频谱同样分布在100 Hz附近，频带较宽，且幅值明显高于正常振动信号；互感器振荡故障振动信号的频谱分布在140 Hz～160 Hz和440 Hz～460 Hz范围。

上述说明，基于改进HHT算法的方法对GIS设备的机械振动信号进行时频分析是有效的。通过模拟不同类型的机械故障，最终能够建立GIS机械故障诊断数据库。

参考文献：

[1] RUDD S, MCARTHUR S D, JUDD M D. A generic knowledge-based approach to the analysis of partial dischargedate[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(1)：149-156.

[2] 徐天乐，马宏忠，陈楷，等. 基于振动信号HHT方法的GIS设备故障诊断[J]. 中国电力，2013, 39(3):39-42.

[3] 程林. 特高压GIS/HGIS设备振动诊断方法研究[J]. 电力建设，2009, 30(7):17-19.

[4] 黄金剑，杨宝琨. 基于振动信号的GIS机械状态检测系统及其应用[J]. 广西电力，2015, 38(5): 55-59.

[5] 李天云，赵妍，季小慧，等.HHT方法在电力系统故障信号分析中的应用[J].电工技术，2005,20(6)：87-91.

[6] 陈隽，徐幼麟. HHT方法在结构模态参数识别中的应用[J]. 振动工程，2003,16(3): 383-388.

[7] 李婷，蒋庆，蔡晋辉，等. 小波消噪-HHT的四通阀故障诊断[J]. 中国计量，2009,20(3): 235-239.

[8] WU ZHAOHUA, HUANG NORDEN E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Date Analysis, 2011,1(01):1-41.

[9] 朱宁辉，白晓民.基于EEMD的谐波检测方法[J].中国电机工程学报，2013，33(7):92-98.