基于相空间重构和SVR的磨煤机故障预测研究
李德忠, 杨 柳, 胡 蓉, 任资龙, 谢小鹏, 向春波
(湖南大唐先一科技有限公司, 长沙 410007)
电站磨煤机作为锅炉燃烧制粉系统的核心设备,其工作状况对整个电厂系统运行的安全和经济性具有重要的影响。在火力发电机组等效非计划停运的所有影响因素中,磨煤机故障是主要原因之一,其故障直接影响了锅炉机组运行稳定性、燃烧经济性和机组出力。因此,研究磨煤机的故障诊断具有重要意义[1]。
由于火电厂磨煤机运行环境的复杂性,磨煤机的故障过程中存在着不确定性:同一故障类型表现为多种不同的故障征兆;往往不同故障类型也可能产生不同的故障征兆;不同故障征兆之间往往也存在相互关联的关系。传统的故障诊断方法往往很难取得理想的效果[2]。
近年来,在机器学习领域中备受瞩目的支持向量回归机(SVR)在许多领域得到了成功的应用,显示出巨大的优越性:SVR计算的复杂度与训练样本变量的维数无关,能有效解决高维问题。目前广泛使用的统计故障诊断方法包括主元分析法(PCA)、Fisher判别分析法(FDA)和独立成分分析法(ICA)[3]。这些方法都是线性降维方法,即假设变量之间满足线性相关关系,可通过降维和提取独立变量来实现故障诊断;但对于磨煤机这种复杂过程,变量之间往往呈现出强耦合性和非线性关系,需采用非线性方法对磨煤机进行故障诊断[4-6]。因此,笔者采用SVR对火电厂数据进行预测。
1 预测模型
1.1 标准化处理
采用标准分数对数据进行处理,可以反映一个数据距离平均数的相对标准距离,公式如下:
(1)
式中:xij为第i条数据的第j个测试特征。
通过式(1)对数据进行标准化之后消除了量纲对数据的影响,原始数据低于平均值的时候为负数,高于平均值的时候为正数。标准化后的每一列数据的平均值为0,方差为1,而且近似服从正态分布。
1.2 基于频率分布的一阶向前差分去噪法
因为数据的差分值反映了数据的波动情况,笔者研究了设备各个指标的一阶向前差分绝对值的频率直方分布图,发现差分绝对值小的部分频率高,差分绝对值大的地方频率却很低, 因此差分绝对值比较大的部分所对应的数据更容易是异常数据。算法的基本思想是:
ci=xi+1-xi
(2)
di=|xi+1-xi|,i=1,…,n-1
(3)
式中:xi为第i条测试数据。
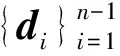
这种方法既可以找出孤立异常点还可以找出连续s个点以内的异常段,去掉的异常点用线性插值补全。
(3) 线性插值补全。
设去除的异常点为xi+1,xi+2,…,xi+s(s≥1),则由线性插值法得出去除的异常点补全后对应的点为:
(4)
1.3 SVR模型
SVR采用结构风险最小化原则,通过适当的非线性变换将输入空间变换到一个高维特征空间,把在这个特征空间中寻找线性回归最优超平面归结为求解凸规划问题,并求得全局最优解。SVR具有很好的泛化能力。
在SVR中,通常采用如下的ε不敏感损失函数,即
(5)
式中:f(x)为学习函数;(x,y)为训练样本;ε为拟合精度。
SVR的目标是寻找一个函数f(x)=ωTφ(x)+b(φ(x)为x到高维空间的非线性映射函数;ω为学习函数的广义参数;b为分类阈值),使得它与所有训练点的实际输出yi的背离尽可能不超过ε,同时函数尽可能平坦。当误差小于ε时,对其不予考虑,只考虑大于ε的误差,多出的误差通常用松弛因子ζi和ζi*表示。
给定训练样本(xi,yi)(i=1,2,…,l),其中xi∈Rm,yi∈R。根据结构风险最小化准则,SVR模型的优化目标为:
约束条件为:
式中:C为用于控制对超出ε的样本的惩罚程度。
SVR模型的一个重要概念是核函数,由Mercer定理可得,核函数K(xi,xj)和φ(x)满足:
K(xi,xj)=φ(xi)·φ(xj)
(6)
原始优化问题可以转化为对偶问题:
约束条件为:
对应的KKT(Karush-Kuhn-Tucker)条件为:
当所有的拉格朗日算子αi和αi*满足KKT条件时,解是最优的。
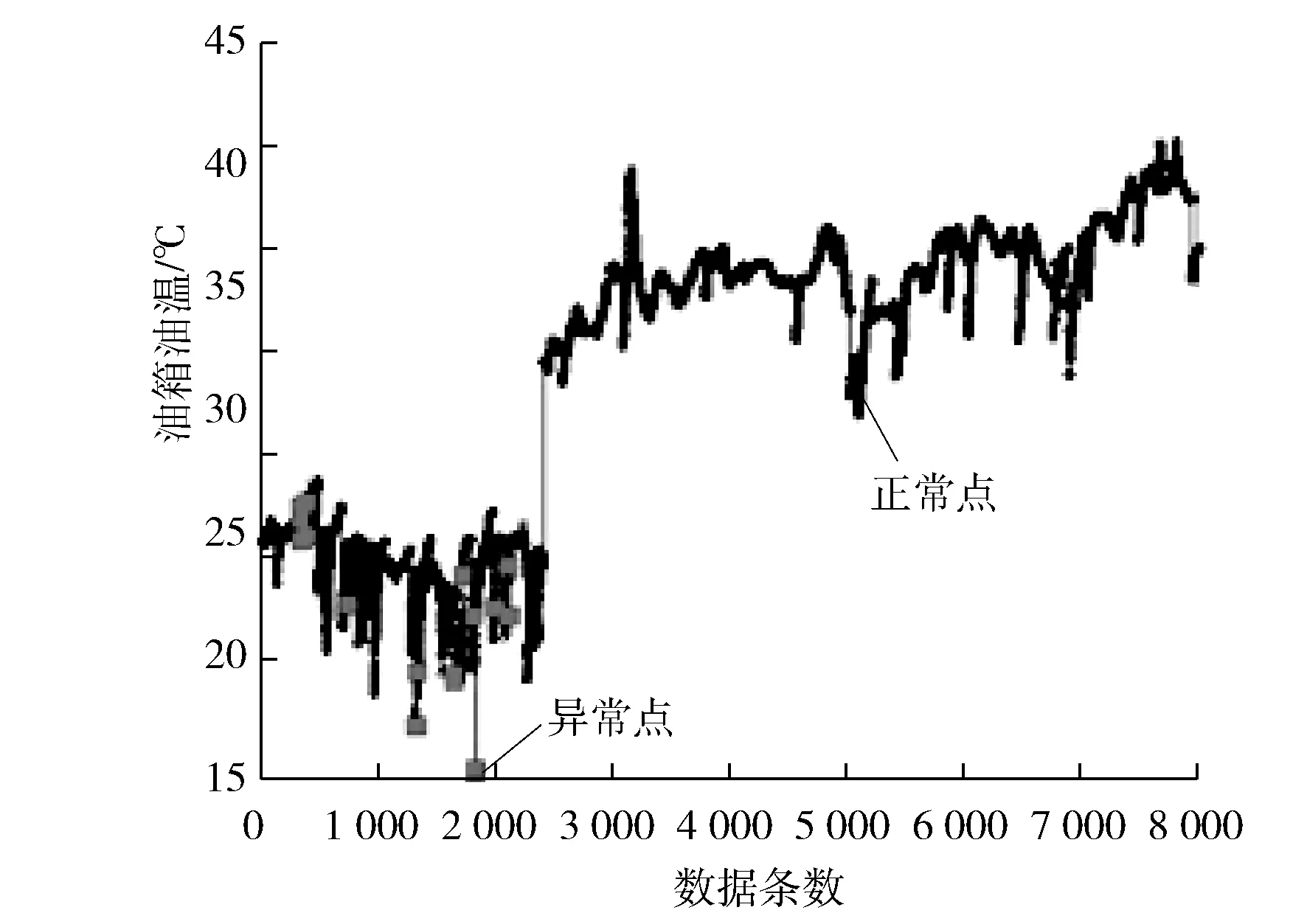
由KKT条件可以看出:当αi=0且αi*=0时,训练点(xi,yi)是位于ε带子区域(f(x)±ε)之内(包括边界);当0<αi 求出αi和αi*(i=1,…,l)后,偏置项b的求取方法为:当0<αi 通过SVR模型可得到回归函数如下: (7) 式中:βi为系数,βi=αi-αi*(i=1,…,l)。 训练样本数据采集于某电厂320 MW机组磨煤机的实际生产过程。输入参数为磨煤机的电动机电流、润滑油温度、油位变化、减速润滑油温、油箱油温、左侧轴承温度1、左侧轴承温度2、右侧轴承温度1、右侧轴承温度2、油箱油位、小牙轮轴承温度1和小牙轮轴承温度2共12个参数。选取一年的数据作为试验数据,共8 000。 实际上数据的采集往往不完整,导致数据缺失的因素有很多,例如传感器故障、通信线路及人为等因素都会导致一些数据的不完整[5]。采用一阶向前差分去噪法对训练样本进行了异常数据剔除和缺失数据修补。图1为样本数据中磨煤机油箱油温的数据剔除情况。 图1 磨煤机油箱油温的数据异常点 12个指标的数据剔除情况见表1。笔者为了消除量纲对数据的影响,避免个别特殊变量在故障诊断中占主要地位,对原始数据进行了标准化处理。 表1 训练样本数据中各指标中异常数据的个数 假设某一设备的训练样本是M维多变量时间序列{x1,x2,…,xN},xi=(x1i,x2i,…,xMi),N表示样本个数。根据时间延迟的思想,多变量时间序列延迟相空间重构的相点为: (8) (9) 映射fi即为前面所叙述的根据SVR所得出的预测函数。 为了验证相空间重构与SVR模型磨煤机故障预测的性能,研究通过在Matlab平台上的仿真试验对所提的方法进行评估。文献[7]认为径向基函数在处理非线性样本时比线性函数好,而多项式核函数因其参数较多,且当其阶次较高时会导致数值计算困难,将消费大量资源和时间,所以笔者采用通用径向基函数作为SVR模型的核函数,C=10,宽度系数σ=0.1。 在试验中,分别对12维数据进行训练,得到相应的预测模型,再对测试样本进行预测。图2为以磨煤机油箱油温的训练结果。从图2中可以看出:磨煤机油箱油温的预测值和真实值之间的误差较小,各维参数训练后的最大均方根误差为8.76。图3为测试数据中磨煤机油箱油温的预测结果。 图2 训练样本中真实值、预测值及误差 图3 测试数据中真实值、预测值及误差 由图3可见:预测值与真实值基本吻合,预测效果较好,测试集所有维度的最大均方根误差为0.8。预测结果表明提出的基于SVR数据预测方法可以达到预期效果。采用这种SVR预测方法,将磨煤机运行的历史数据作为样本进行训练,获得训练模型,再将从分布式控制系统(DCS)采集的特征参数输入模型进行实时的预测,通过预测值与真实值之间的比对,可为电站磨煤机故障实时监测与预测提供一种重要的手段。 为了评估模型的逼近能力,采用均方根误差XRMSE进行评价,其计算公式如下: (10) 式中:yt*为yt的逼近值。 为了评价模型的预测效果,采用均方根相对误差XRMSRE进行评价,其计算公式如下: (11) 训练集的最大均方根误差为8.76,测试集的最大均方根误差为0.8(见表2),均满足预测要求。 表2 各指标训练和测试结果均方根误差 为了满足大型机组的安全经济运行,笔者提出一种基于相空间重构和SVR的在线估计和监测方法。通过现场设备实时采集的数据,采用SVR实现对设备的实时动态建模,能够实时对参数进行预测,发现异常实现故障早期预警。通过某电厂320 MW机组的数据仿真,验证了该磨煤机状态监测方法的准确性和有效性。基于相空间重构和SVR的磨煤机故障诊断模型,为电站磨煤机故障实时诊断与预测提供了一种重要的手段,具有快速和适应范围广等优点。 参考文献: [1] 杨雁梅. 电站磨煤机状态监测与故障诊断的研究[D]. 北京: 北京交通大学, 2007. [2] 陈斌源, 朱军. 基于径向基函数神经网络的中速磨煤机故障诊断[J]. 发电设备, 2011, 25(5): 323-326. [3] 纪舜尧. 主元分析在电厂故障诊断中的应用[D]. 北京: 华北电力大学, 2014. [4] 刘定平, 叶向荣, 陈斌源, 等. 基于核主元分析和最小二乘支持向量机的中速磨煤机故障诊断[J]. 动力工程, 2009, 29(2): 155-158. [5] 韩平, 王天堃, 孟永毅. 基于LS-SVM的一次风机振动在线监测及故障预警研究[J]. 机电工程, 2016, 33(5): 629-632. [6] 韩中合, 焦宏超, 徐搏超, 等. 基于EEMD样本熵和SVM的振动故障诊断研究[J]. 汽轮机技术, 2015, 57(6): 457-460. [7] LIN H T, LIN C J. A study on sigmoid kernels for SVM and the training of non-PSD Kernels by SMO-type Methods[J]. Submitted to Neural Computation, 2003,27(1):15-23.2 预测参数选取及评估方法

3 仿真试验及结果
3.1 设备数据多变量时间序列的相空间重构
3.2 SVR训练及预测
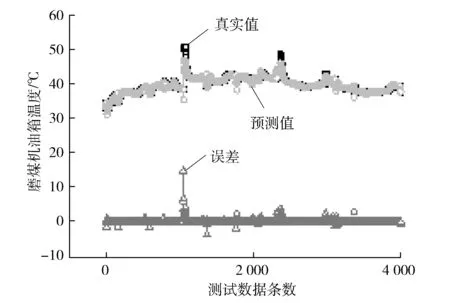
3.3 模型评价
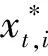
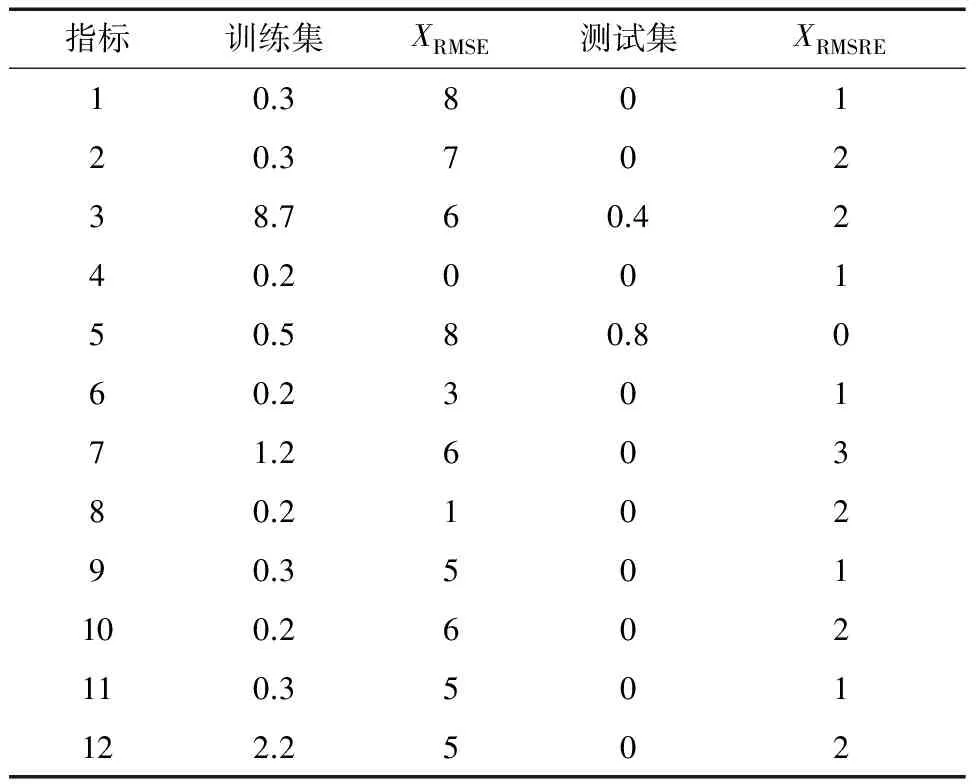
4 结语

