基于Na2HPO4·12H2O相变储能热管理的储热过程研究
张怡秋,程 傲,李小波
基于Na2HPO4·12H2O相变储能热管理的储热过程研究
张怡秋,程 傲,李小波
(华中科技大学能源与动力工程学院,湖北 武汉 430074)
文章研究了水合盐相变储能材料Na2HPO4·12H2O在发热器件热管理上的应用。在储热块的封装中,为了解决水合盐导热性能差的问题,将Na2HPO4·12H2O填充在泡沫金属中以增强其换热;并采用不同厚度的铜片均热板对发热源的均热效果进行测试。通过测试在不同加热功率下均热板中心与边缘位置的温度,发现其温差随均热板厚度增大而减小。在6 W功率加热下,若使均热板温差不超过4 ℃,则均热板厚度应不小于0.5 mm;设定陶瓷片热点温度不超过70 ℃时,30 mm×30 mm×7 mm的储热块可以维持大概10 min。在非稳态储热过程的模拟中,由于Na2HPO4·12H2O具有两个明显的相变区间,传统的考虑单相变点的模拟方法无法给出准确的温度响应,因此采用等效热容法考虑两个相变点进行了数值模拟,结果表明,低功率加热时,采用两个相变点的方法精度更高;而在高功率时,两种方法区别不大。
十二水磷酸氢二钠;相变储能热管理;等效热容法
随着电子器件的高功率及轻薄化发展,其散热问题变得日益严峻,并直接影响电子元器件的使用性能与寿命,也逐渐成为限制电子设备进一步发展的主要瓶颈之一。电子设备一般具有间歇式的工作特点,其平均功耗可能比较低,短时间功耗却可以很高,而在热设计中,必须匹配最大的散热量,以保证设备能在所有工况下正常工作。为了解决这个矛盾,利用热储能技术的热管理技术被认为在此类应用中具有重要的前景[1-4]。
相变材料主要分为无机类(结晶水合盐、熔融盐、金属合金等)、有机类(石蜡、烷烃、脂肪酸等)和有机无机复合相变材料等[5]。在以往的相变储能热管理研究中,大多采用石蜡、烷烃、脂肪酸类相变材料。石蜡、烷烃、脂肪酸类材料具有性质稳定的优点,被诸多文献所报道研究[5-14]。无机水合盐是中低温相变的一类重要材料,具有单位体积熔化潜热大的优点,在轻薄电子器件的热管理中相比其它材料具有先天的优势。这里需要特别说明,无机水合盐的脱水以及结晶过程,属于热化学过程,本文所说的无机水合盐相变不是指一般的物理中的固液“相变”,而是广义上的两种物质以及其形成的化合物在相图上的相互转化。无机水合盐相变材料使用较多的主要是碱及碱土金属的卤化物、硝酸盐、硫酸盐、磷酸盐、碳酸盐及乙酸盐等[15-17]。另外,由于此类相变储能材料的导热系数普遍比较低,在增强材料导热系数方面,金属泡沫、纳米碳管、石墨烯等高导热添加物被广泛研究[18-20],改进后的导热系数一般随高导热添加物比例的增大而增大。其中,TAN等[21]在PDAs的储热单元中填充正二十烷相变材料,可维持PDAs芯片温度低于所允许的温度上限50℃超过2 h,成功实现了相变材料在电子器件热管理中的应用。高学农等[22]以PEG1000为相变材料,膨胀石墨(EG)为载体基质,采用物理吸附法制备出导热系数高、热响应速度快的PEG1000/EG复合相变材料,研究表明,散热器填充复合相变材料后的散热性能明显优于填充前。BABY等[23]选择一种有机相变材料用于电子器件热管理,设计铝翅片增强散热器的导热性能,实验结果良好。王杰利等[24]提出了一种封装有金属泡沫和相变材料的复合式散热器。此外,合金材料用于相变储能热管理也有一些报道[25]。
水合盐类相变储能材料具有较高的单位体积储能密度,而水合盐用于相变储能热管理的研究尚不充分,因此本文采用十二水磷酸氢二钠(Na2HPO4·12H2O)作为相变材料,研究了其在发热器件热管理上的应用。具体内容包括:制造Na2HPO4·12H2O复合相变储热块,采用不同功率加热来检验储热块的储热能力,并探究均热板厚度对其加热表面温差的影响。同时采用等效热容法[26]研究了十二水磷酸氢二钠这种具有两个相变区间的材料在储热工程中的温度响应,并与实验对比。
1 实验原理
十二水磷酸氢二钠(Na2HPO4·12H2O)是一种较好的低温高储能密度材料[27]。文献显示其熔点为35.5 ℃,质量计相变潜热为280 kJ/kg,体积计为426160 kJ/m3 [3]。研究发现,Na2HPO4·12H2O在35 ℃左右脱水成Na2HPO4·7H2O,Na2HPO4·7H2O在43 ℃左右脱水成Na2HPO4·2H2O,具有两个不同的相变温度[28]。我们试验中采用的十二水磷酸氢二钠(Na2HPO4·12H2O),纯度为99.0%,购买于国药集团化学试剂有限公司;泡沫金属采用泡沫铜,厚度为7 mm,孔隙率约为94.4%;底部和加热片贴合的铜片厚度分别为0.2 mm、0.5 mm和1.0 mm;封装用环氧灌封胶购买于奥斯邦(中国)有限公司;温度数据用KEITHLEY 2700进行采集;热电偶为K型;发热源采用陶瓷加热片,由直流稳压电源供电。
储热模块的制备过程如下:①分别采用厚度为0.2 mm、0.5 mm、1.0 mm的铜板作为均热板,铜板长宽留有余量,中间放上事先准备的30 mm×30 mm×7 mm尺寸的模具,四周用环氧灌封胶封装,固化24 h达到需要强度;②将尺寸为30 mm×30 mm×7 mm的泡沫铜浸没入融化的Na2HPO4·12H2O液体中,将浸没过的泡沫铜填入制作好的模型中,稍作冷却;③在缝隙处填入融化的Na2HPO4·12H2O液体,全程采用的电子天平称量,确保各储热块中泡沫铜和Na2HPO4·12H2O的质量及比例一致,分别为4.80 g和13.30 g;④完全冷却后,在模型的上方加入环氧灌封胶封装,最后固化24 h,制成复合相变材料储热块。
储热模块的热管理测试如图1所示。在储热块的均热板正中心涂导热胶放置10 mm×10 mm的电阻加热片,加热片和铜板之间正中心布置热电偶1,距离中心15 mm的位置布置热电偶2,均热板朝下,下加泡沫保温层,分别给电阻加热片加2 W、4 W、6 W的功率,热电偶通过数据采集仪连接计算机采集并记录温度随时间的变化,采集间隔为1 s。
2 实验结果
对均热板厚度为1.0 mm、0.5 mm和0.2 mm的储热块,分别加上2 W、4 W和6 W的功率,记录了均热板正中心和15 mm位置温度,如图2所示,图2(a)~(c)分别表示了1.0 mm、0.5 mm和0.2 mm厚的均热板分别在2 W、4 W和6 W的加热功率下的温度曲线。
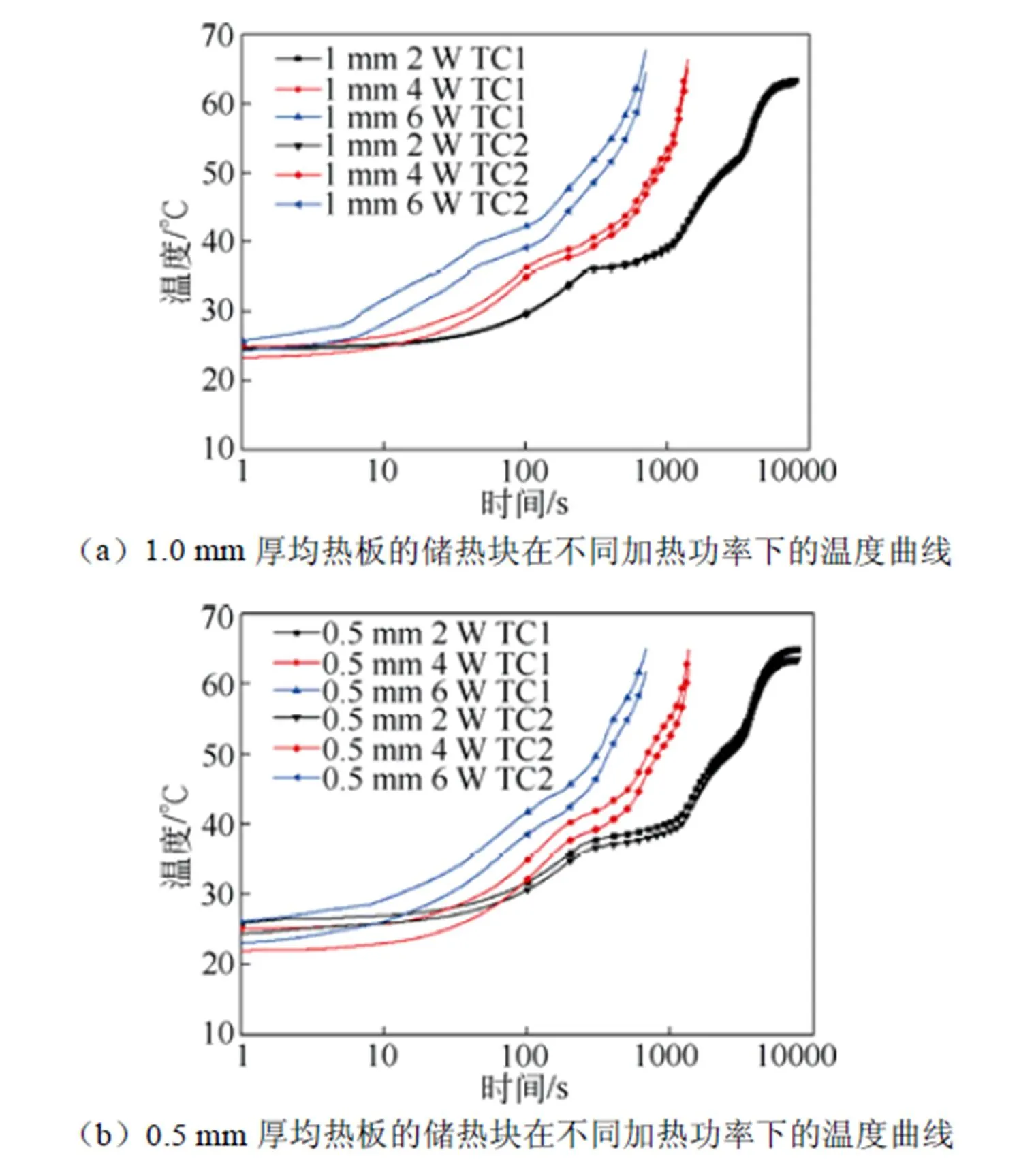
由图2(a)可以看出,1.0 mm厚的均热板在低功率2 W加热下,温差很小,只有0.5 ℃左右,在4 W加热功率下温差也只有1.0 ℃左右,6 W时有3.0 ℃,可见,1.0 mm的均热板能有效均热,减少加热时带来的局部温升高的问题。
由图2(b)可以看出,0.5 mm厚的均热板在低功率2 W加热下,温差也很小,只有1.0 ℃左右,在 4 W加热功率下温差2.5 ℃左右,6 W时也只有 3.0 ℃,可见,0.5 mm的均热板也能在高功率加热时有效均热,减少局部温升高的问题。
由图2(c)可以看出,0.2 mm厚的均热板在低功率2 W加热下,温差达到了4.0 ℃左右,在4 W加热功率下温差有8 ℃,6 W时甚至高达12 ℃,可见,0.2 mm的均热板并不能有效均热,在热源面积较小、高功率加热条件下热源位置的温度会过高。
为了直观的了解均热板厚度与温差的关系,当储热块相变平稳时,取中心测温点TC1温度为40 ℃的时刻,测温点TC1与边缘测温点TC2温差,绘制温差与均热板厚度关系图,如图3所示。
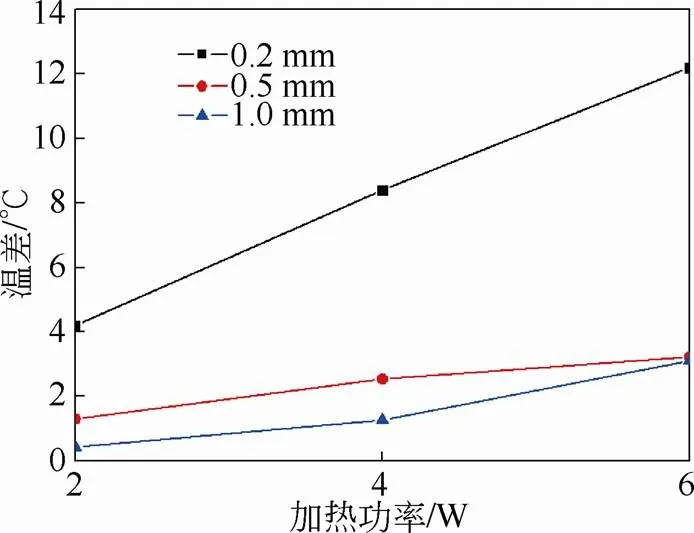
图3 温差与均热板厚度关系图
由图3可以看出,随着均热板厚度的增加,温差呈现先降低后逐渐平稳的趋势,这说明一定的均热板厚度能有效满足在高功率加热条件下均热的效果,若要求此储热块在6 W的加热功率下,均热板的温差不超过4 ℃,则0.5 mm厚均热板可以满足要求。
在储热块体积一定时,储能模块的有效工作时间随着加热功率的增加逐渐变短,设定陶瓷片热点温度不超过70 ℃,满足电子器件热管理需求,实验观察到此时相变材料都已融化完全,在低功率2 W加热时,储热块的储热时间较长,高达4600 s,在较高功率6 W加热时,持续时间约为10 min,2 W时对流散热影响比较大,6 W加热10 min过程中,加入的热量为3600 J,而13.3 g的材料相变潜热约为3724 J,与结果基本一致。
3 理论模拟
对于凝固/融化问题,传热微分方程表示为式(1)
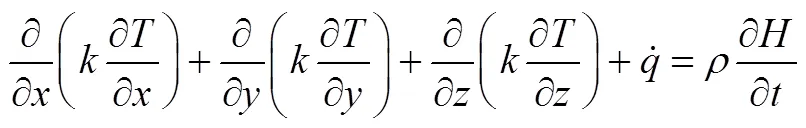
焓定义为显焓和相变潜热量Δ之和:
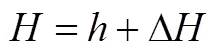
可得:

代入式(1)中得式(4)

定义式(5)为等效热容
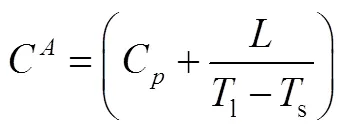
则:
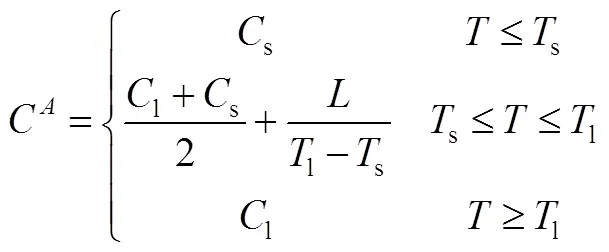
将式(6)代入式(4),得到等效热容法的传热微分方程式(7)
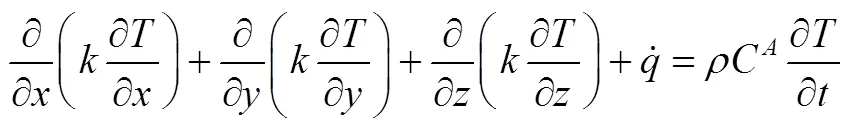
通过求解式(7)可得到温度场的分布。
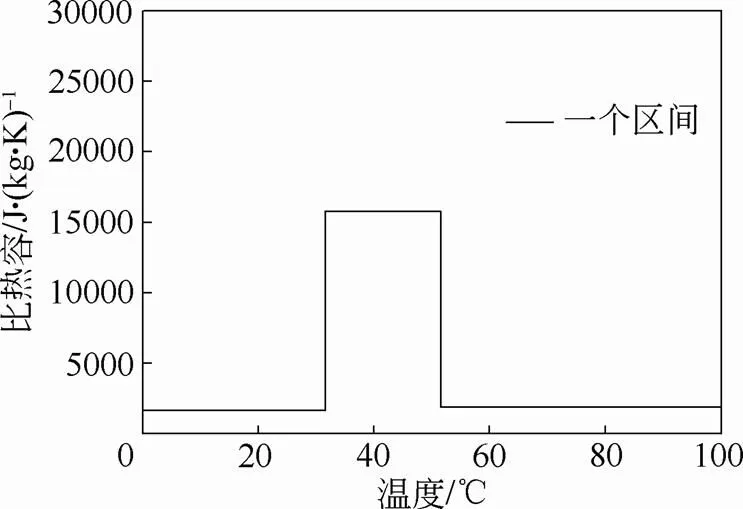
采用等效热容法进行仿真计算,将材料相变区间视为一个整体,以及视为两个连续的区间,相变区间及相变潜热使用文献[3, 28]数据,得表1。将数据输入软件COMSOL中。两种方法的等效热容图如图4所示。
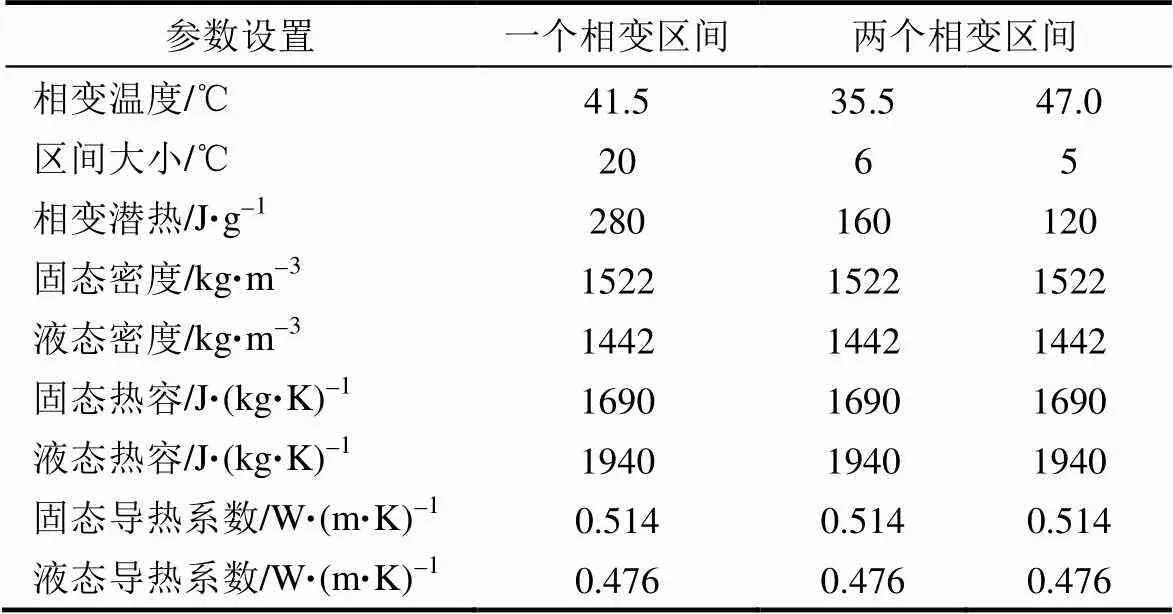
表1 材料模拟参数设置表
在COMSOL软件中构造储热块的三维几何模型,其中只对比1.0 mm厚均热板的储热块瞬态加热过程,模型采用上下两层体结构,分别由上面30 mm×30 mm×7 mm的复合材料和下面30 mm×30 mm×1 mm的均热板组成。上层体中泡沫铜设置为孔隙率为94.4%多孔介质,泡沫铜和均热板都采用系统默认的铜材料物性参数,四周和上面的封装材料做简化处理,边界条件设置自然对流换热,均热板底面正中心1 cm×1 cm的面积设置热流入口,因此热流密度分别是2 W/cm2、4 W/cm2和6 W/cm2,底面其余部分设为绝热表面,仿真计算,取均热板正中心测温数据,得到结果如图5(a)~5(d)所示,这些分别表示1.0 mm厚的均热板在2 W、4 W和6 W的加热功率下,视为一个整体和视为两个连续的相变区间,温度曲线与实验测得的数据对比。

图5 1.0 mm厚均热板的储热块在不同加热功率下视为一个区间和两个区间仿真结果对比图
由图5可以看出,图5(a)在2 W低功率加热下,运用两个连续的相变区间仿真计算的结果更接近真实结果,因为此时双相变点被充分考虑;图5(b)在4 W较高功率下,视两个连续的相变区间的仿真结果基本拟合真实结果,一个区间的拟合稍有偏差,且三条曲线斜率在相变过程中变化不大,说明随着功率增大,材料双相变点的影响逐渐变小;图5(c)在6 W高功率下,视为一个整体和两个连续的相变区间的仿真结果都接近真实结果,且不能完全拟合,因为此时传热速率和周围环境对流换热的影响大于双相变点的影响。
可见,对于非固定相变点的材料的仿真,低功率加热时应考虑多个相变点的影响,视为两个连续的相变区间计算,精度更高;高功率加热时视为一个相变区间也可以得到高精度结果,且计算更节约时间。
4 结 论
本文构造了不同厚度均热板的Na2HPO4·12H2O-泡沫铜储热块,在不同功率下加热,得到均热板中心与边缘温度及温差。实验测试结果表明,储热块可以维持CPU在较高加热功率6 W下工作10 min;均热板温差随厚度增大而减小,在6 W加热功率下,若使温差不超过4 ℃,则厚度应不小于0.5 mm。
对于非固定相变点材料Na2HPO4·12H2O,采用等效热容法分别视为一个整体和视为两个连续的相变区间进行仿真计算。结果表明,低功率加热时,分为两个连续的相变区间计算精度更高;高功率时,两种方法都接近实验结果,视为一个相变区间计算效率更高。
[1] FARAJI M, QARNIA H E. Passive cooling of protruding electronic components by latent heat of fusion storage[J]. Journal of Electronic Packaging, 2009, 131(5): 1-10.
[2] AGYENIM F, HEWITT N, EAMES P. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS)[J]. Renewable and Sustainable Energy Reviews, 2010, 14(2): 615-628.
[3] 张寅平, 胡汉平, 孔祥东, 等. 相变贮能——理论和应用[M]. 合肥: 中国科学技术大学出版社, 1996.
ZHANG Yinping, HU Hanping, KONG Xiangdong, et al. Phase change storage theory and application[M]. Hefei: University of Science and Technology of China Press, 1996.
[4] AI HALLAJ S, SELMAN J R. Thermal modeling of secondary lithium batteries for electric vehicle/hybrid electric vehicle applications[J]. Marine Electric & Electric Technology, 2004, 110(2): 341-348.
[5] ABHAT A. Low temperature latent heat thermal energy storage: Heat storage materials[J]. Solar Energy, 1983, 30(4): 313-332.
[6] DINCE R, IBRAHI M. Thermal energy storage: Systems and applications[M]. 2nd ed. New York: Wiley, 2011.
[7] HAWES D W, FELDMAN D, BANU D. Latent heat storage in building materials[J]. Energy & Buildings, 1993, 20(1): 77-86.
[8] LANE D G A. Low temperature heat storage with phase change materials[J]. International Journal of Ambient Energy, 1980, 1(3): 155-168.
[9] SASAGUCHI K, VISKANTA R. Phase change heat transfer during melting and resolidification of melt around cylindrical heat source(s)/sink(s)[J]. Journal of Energy Resources Technology, 1989, 111(1): 43-49.
[10] FELDMAN D, SHAPIRO M M, BANU D. Organic phase change materials for thermal energy storage[J]. Solar Energy Materials, 1986, 13(1): 1-10.
[11] DIMAANO M N R, WATANABLE T. The capric-lauric acid and pentadecane combination as phase change material for cooling applications[J]. Applied Thermal Engineering, 2002, 22(4): 365-377.
[12] ROXAS-DIMAANO M N, WATANABLE T. The capric and lauric acid mixture with chemical additives as latent heat storage materials for cooling application[J]. Energy, 2002, 27(9): 869-888.
[13] SARI A, KAYGUSUZ K. Thermal performance of palmitic acid as a phase change energy storage material[J]. Energy Conversion & Management, 2002, 43(6): 863-876.
[14] SARI A, KAMIL K. Thermal energy storage system using some fatty acids as latent heat energy storage materials[J]. Energy Sources, 2001, 23(3): 275-285.
[15] ZALBA B, JOSE M M, CABEZA L F. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications[J]. Applied Thermal Engineering, 2003, 23(3): 251-283.
[16] NAUMANN R, EMONS H H. Results of thermal analysis for investigation of salt hydrates as latent heat-storage materials[J]. Journal of Thermal Analysis, 1989, 35(3): 1009-1031.
[17] BELTON G, AJAMI F. Thermochemistry of salt hydrates[R]. Philadelphia. 1973-05-01.
[18] CHEN Z, GU M, PENG D. Heat transfer performance analysis of a solar flat-plate collector with an integrated metal foam porous structure filled with paraffin[J]. Applied Thermal Engineering, 2010, 30(14): 1967-1973.
[19] PINCEMIN S, OLIVES R, PY X, et al. Highly conductive composites made of phase change materials and graphite for thermal storage[J]. Solar Energy Materials & Solar Cells, 2008, 92(6): 603-613.
[20] FUKAI J, KANOU M, KODAMA Y, et al. Thermal conductivity enhancement of energy storage media using carbon fibers[J]. Energy Conversion & Management, 2000, 41(14): 1543-1556.
[21] TAN F L, TSO C P. Cooling of mobile electronic devices using phase change materials[J]. Applied Thermal Engineering, 2004, 24(2/3): 159-169.
[22] 高学农, 刘欣, 孙滔, 等. 基于复合相变材料的电子芯片热管理性能研究[J]. 高校化学工程学报, 2013(2): 187-192.
GAO Xuenong, LIU Xin, SUN Tao, et al. Study on the thermal management performance of electronic chip with composite phase change material[J]. Journal of Chemical Engineering of Chinese Universities, 2013(2): 187-192.
[23] BABY R, BALAJI C. Experiment investigations on phase change material based finned heat sinks for electronic equipment cooling[J]. International Journal of Heat and Mass Transfer, 2012, 55(5/6): 1642-1649.
[24] WANG J L. Experiment study of hybrid heat sink sintered with mental foams filled with phase change materials[J]. Journal of Engineering Thermophysics, 2011, 32(2): 295-298.
[25] KRISHNAN S, GARIMELLA S V. Thermal management of transient power spikes in electronics-phase change energy storage or copper heat sinks?[J]. Journal of Electronic Packaging, 2004, 126(3): 363-374.
[26] VOLLER V R, SWAMINATHAN C R, THOMAS B G. Fixed grid techniques for phase change problems: A review[J]. International Journal for Numerical Methods in Engineering, 1990, 30(4): 875-898.
[27] HOFMANN S, DUCATI C, REBERTON J. Low-temperature growth of carbon nanotubes by plasma-enhanced chemical vapor depostion[J]. Applied Physical Letter, 2003, 83(17): 79-83.
[28] HERBERT K, RAINER T. Development of media for dynamic latent heat storage for the low-temperature range. Part 1: Thermal analyses of selected salt hydrate systems[J]. NASA Sti/recon Technical Report N, 1985, 85(2): 132-146.
Thermal management based on Na2HPO4·12H2O phase change heat storage
ZHANG Yiqiu,CHENG Ao,LI Xiaobo
(College of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, Hubei, China)
Salt hydrate based thermal energy storage material, Na2HPO4·12H2O, was studied for thermal management of electronics. Such a material usually has a poor thermal conductivity and hence was filled in a metal foam to enhance the thermal conductivity. Copper sheets with varying thickness were used to study the heat spreading effects on the heating module. With different levels of heating power, the temperature difference between the middle and the edge of the copper spreader was monitored. The results showed that an increase in the thickness of the copper sheet decreases the temperature difference. With 6W heating power, a 0.5 mm thick copper sheet should be used if the required temperature difference is less than 4℃. A heat storage module with a dimension of 30 mm×30 mm×7 mm could work for 10 minutes without overheating above 70℃. Simulations were performed with both one-melting-point model and two-melting-point model. The results showed that the two-melting point model worked better than the one-melting-point model at a low power, whereas little difference between the two models were seen at high powers.
Na2HPO4·12H2O; phase change thermal management; apparent heat capacity method
10.12028/j.issn.2095-4239.2017.0156
TK 02
A
2095-4239(2018)02-0282-06
2017-11-06;
2017-11-26。
张怡秋(1994—),女,硕士研究生,研究方向为高导热复合相变材料的储能,E-mail:zyiqiu@foxmail.com;
李小波,副教授,主要研究方向为热储能,微纳米尺度传热等,E-mail:xbli35@hust.edu.cn。

