锂电池注液工艺中电解液驱替的格子Blotzmann模拟

俞 涛，李顶根，张晓军，戴克文



锂电池注液工艺中电解液驱替的格子Blotzmann模拟

俞 涛1，李顶根1，张晓军2，戴克文2

（1华中科技大学能源与动力工程学院，湖北 武汉 430074；2辽宁陆海石油装备研究院有限公司，辽宁 盘锦 124010）

锂离子动力电池注液工艺中，电解液的驱替效率直接影响后续工艺中固体电解质界面膜（SEI）的成型质量。采用随机生长四参数法，对锂离子电池多孔电极微观结构进行了重构；基于改进的伪势格子Boltzmann模型研究电池注液工艺中的非混相驱替；仿真分析了锂离子电池多孔电极结构的壁面润湿性和孔隙率对驱替效率的影响。研究表明，多孔电极的润湿特性对驱替效率有显著影响，随着接触角增大而驱替效率降低；在单一孔隙率的多孔介质中，随着孔隙率增加而驱替效率增高，被驱替相残留越少，驱替效果越好；但当电解液流经负极和隔膜交界面处时，因两侧润湿特性和孔隙率有差异，会使得电解液在两侧的驱替效率不同，孔隙率大的一侧在垂直流动方向会产生渗流，降低另一侧的驱替效率，产生气泡，影响到SEI膜的成型。

格子Boltzmann；伪势模型；电池注液；驱替效率；

目前，锂离子电池因其高能量密度和高比功率等特性被广泛应用到电动汽车中。而随着其大规模应用，锂离子电池热失控的安全问题成了制约其发展的重要瓶颈。通过对锂离子电池热失控机理的研究发现，SEI膜热分解是热失控中重要环节，而锂离子电池注液工艺中电解液驱替效率直接影响到后续化成工艺SEI膜成型质量[1]。格子Boltzmann方法作为一个新兴的流体力学模拟方法，适合模拟多组分流体在多孔介质中输运，当前格子Boltzmann在多孔介质中的研究集中在单一多孔介质中，尺度涉及到REV尺度、孔隙尺度、宏观区域尺度，探究因素也包括了多孔介质孔隙率、粒径分布等，对多相流在复杂多孔介质区域中的输运研究尚少。注液工艺中电解液驱替过程则是一种非混相驱替过程，该问题涉及到复杂的流体间相互作用和流固间相互作用，而格子Boltzmann方法作为一种连接微观方法和宏观方法桥梁的介观方法被广泛应用在多相流驱替问题中[2-4]。因此本工作采用一种改进的伪势格子Boltzmann模型来研究电解液在复杂电池多孔电极中的非混相驱替问题。

1 模型建立

1.1 多孔介质构建

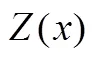
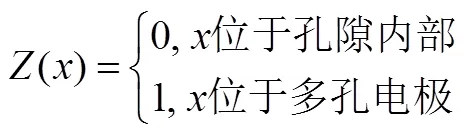
锂离子电池电极由活性材料、固体添加物组成，重建过程中将活性材料和固体添加剂都看作固体电极。如图1所示，图1(a)为锂离子电池负极FIB/SEM照片；图1(b)为重构的多孔电极结构，白色表示多孔电极，黑色表示孔隙区域。

1.2 ShanChan两组分格子Boltzmann模型

SHAN和CHAN[6]在1993年提出一种基于均场理论的多相多组分格子Botlzmann模型，在该模型中，流体间相互作用力采用伪势函数来反应，从而推导出非理想状态方程，所以该模型也被称为ShanChan伪势模型。该模型对微观层面的各种相互作用进行了直观的描述，能够反映多组分多相流的流体动力学的物理本质，使得模型适用于混相和非混相的流体系统[7-8]。而一直以来，研究者们在提高SC计算模型的广度和效率上做了许多改进，如YUAN等[9]和YU等[10]通过改变伪势函数中的有效密度表达式，使得SC模型能够模拟具有大密度比系统。

ShanChan伪势模型中认为多孔介质中存在多种组分，组分的格子Boltzmann方程如式(2)所示

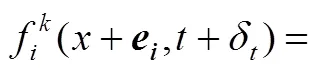
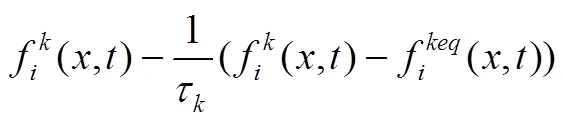
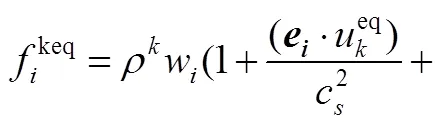
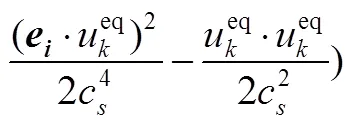
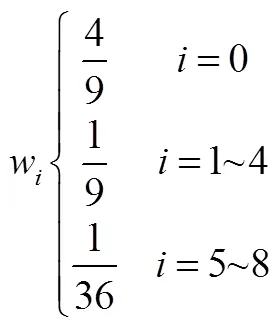
在ShanChan伪势模型中，通过对平衡态分布函数中速度的影响来体现分子间作用力。

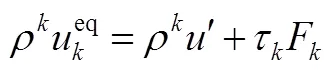
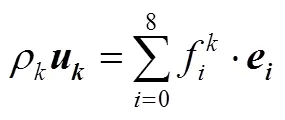
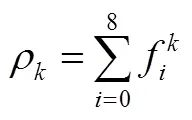
而上述式(2)～式(8)可以通过Chapman-Enskog分析恢复至不可压Naiver-Stokes方程。

ShanChan模型作为一种伪势模型，组分在处受到周围组分分子的作用力使用以下公式来描述

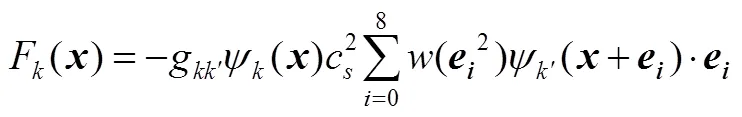
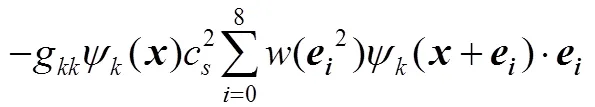
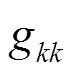
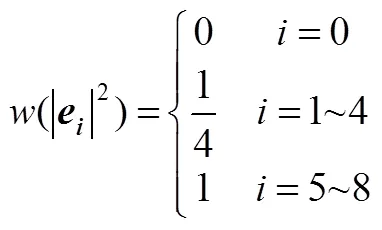
组分在处受到的固体壁面和流体间作用力则采用以下形式来描述

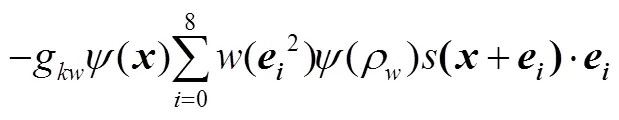
1.3 模型验证

2 模拟结果与分析

图2 泊肃叶流验证

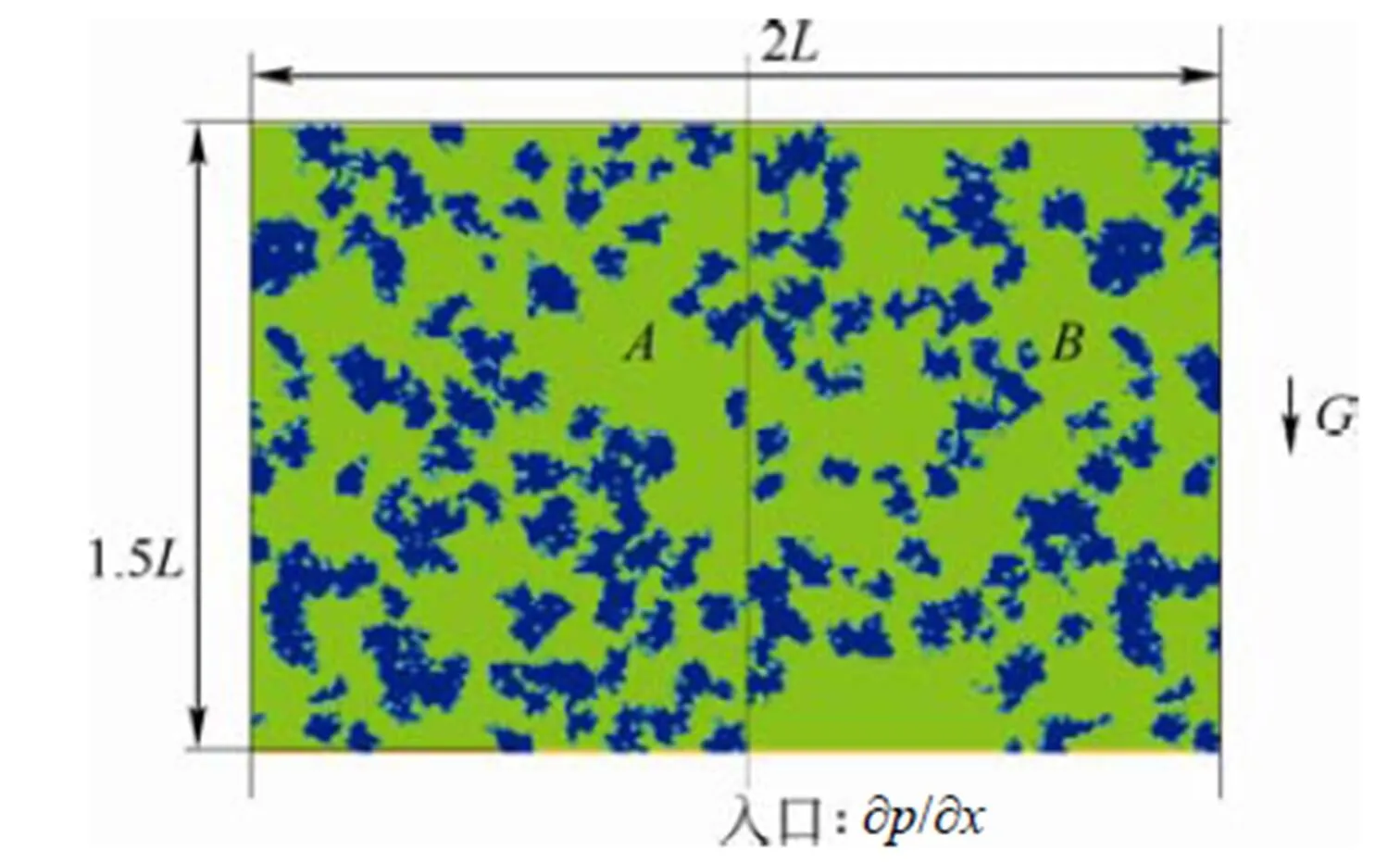
图3 电极结构示意图

2.1 润湿性对注液中电解液驱替的影响

图4 接触角变化

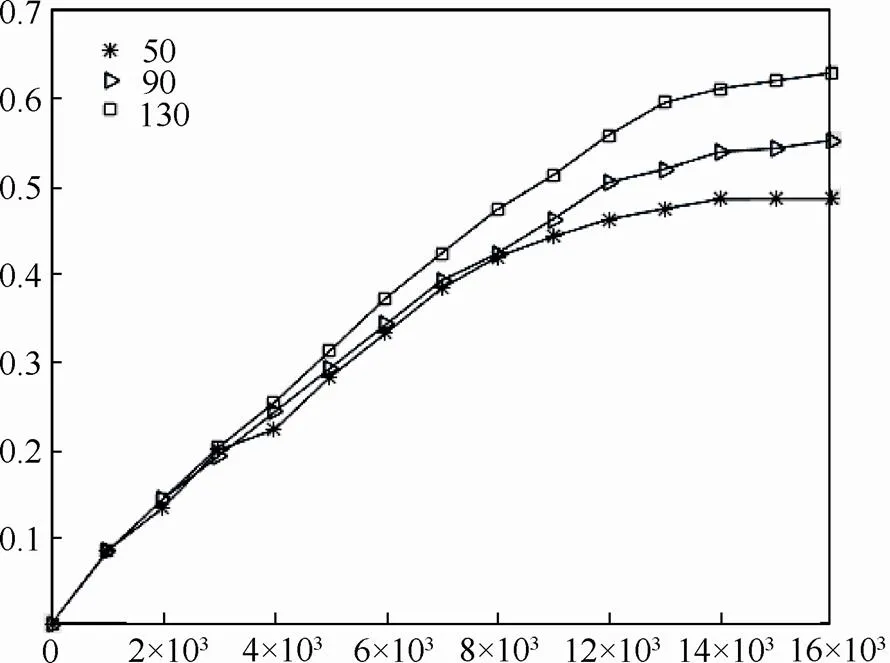
图5 不同润湿性下饱和度曲线

当壁面处于润湿性强的时候，即三相接触角小时，电解液具有较强的黏附力，难以和壁面脱离，并且更容易在压力驱动下在多孔电极内部流动，随着接触角的增加，驱替的效果越来越差。当接触角大于90°后，壁面呈现非润湿性，黏附力变小，电解液更快流经多孔电极，容易与残余空气形成气泡结构从而影响到电解液的分布。从模拟结果来看，接触角越大，电解液的饱和度曲线更快达到最大值，驱替时间减小，但驱替效率变差。综上所述，减小接触角对驱替过程有利。

2.2 孔隙率对注液中电解液驱替的影响

采用LBM模拟当电解液经过两种不同孔隙率多孔介质时饱和度曲线变化，A区域多孔介质孔隙率为0.55，B区域多孔介质孔隙率为0.65。图8为该情况下两个区域饱和度曲线图，多孔电极A区域的饱和度曲线较之单一孔隙率情况下，整体有所左移，而多孔电极B区域的饱和度曲线较之单一孔隙率情况下，整体有所右移。因为电解液在孔隙率较大的区域中，流动较快，沿着孔隙率大的区域中的大孔道流动，而在两种多孔介质直接接触的地方，存在横向渗流，孔隙率大区域中的电解液会向未饱和的孔隙率小的区域渗透，从而使得孔隙率小的区域提前饱和。但这种从侧向进入多孔介质区域的电解液会和多孔介质一起形成对小孔隙区域中电解液的阻塞，所以在孔隙率小的区域形成气泡，使孔隙率小的区域的最大饱和值较之没有渗流存在时有所降低，而大孔隙率区域则并不会因为横向渗流的存在而使得最大饱和值降低，只会因此而推迟达到最大饱和值的时间，时间推迟大概30%左右。

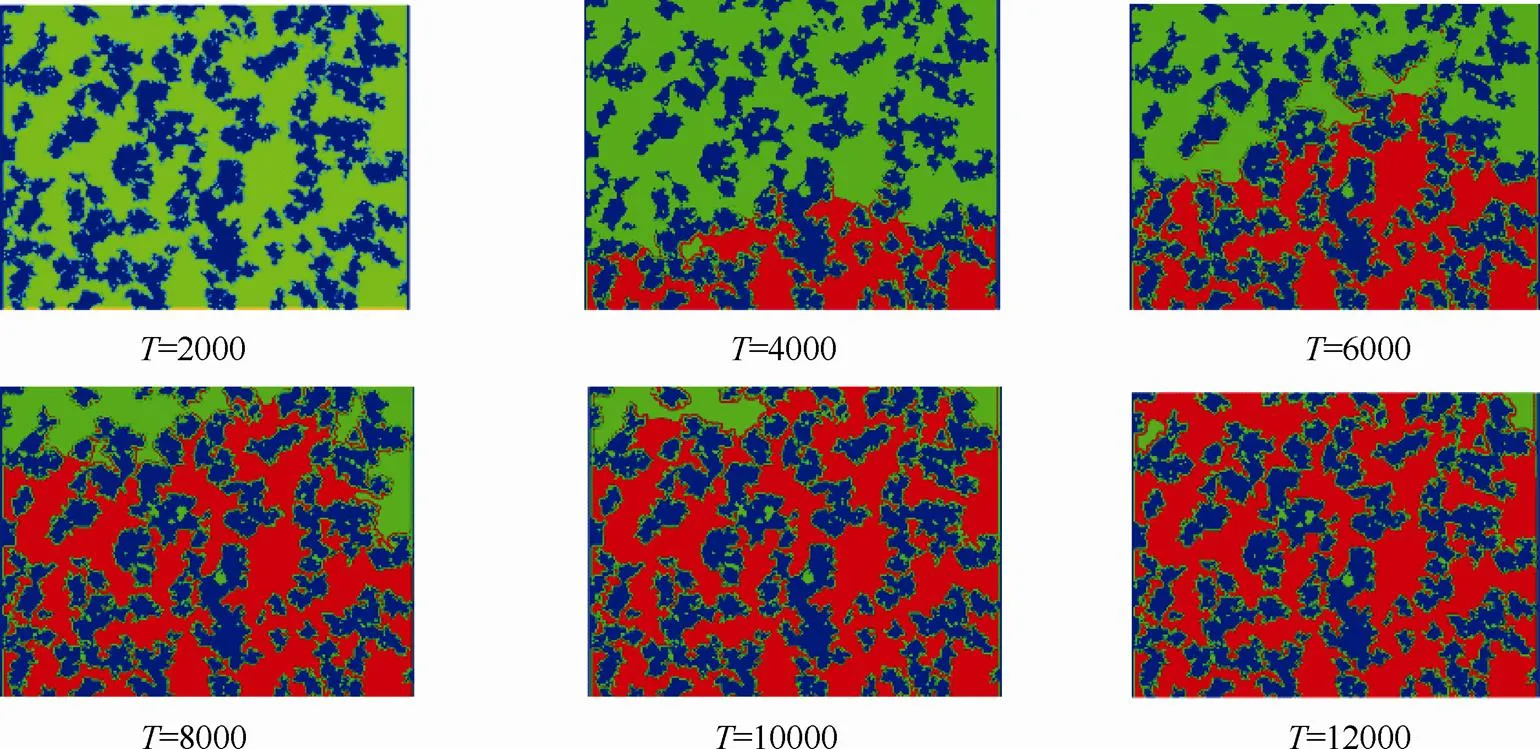
图6 电解液输运随时间变化

图7 不同孔隙率下的饱和度曲线

3 结 论

研究表明：①壁面润湿性的增强，会使饱和度曲线提前达到饱和，并增大饱和度曲线的最大值，意味着驱替的时间减少，但饱和度曲线并不能达到孔隙率，这是因为多孔介质和电解液会阻挡残余空气排出的通路，从而在电池中形成微小气泡，影响到SEI膜的形成，降低驱替效率；②孔隙率越大，会使饱和度曲线最大值与孔隙率之间的差值越小，说明孔隙率越大的多孔介质，越难以形成微小气泡结构，越容易让电解液填满整个孔隙区域；③电解液流经不同孔隙率的多孔介质时，在孔隙率较大的区域流动较快，所以会产生横向渗流，影响到孔隙率小的区域的驱替效果，会使小孔隙率区域更快达到饱和度曲线的最大值，但此时最大值小于电解液流经单一孔隙率多孔介质时的饱和度曲线最大值，说明产生的横向渗流和多孔电极一起影响到了电解液驱替残余空气的效果，而大孔隙率区域则更慢达到饱和度曲线最大值，但此时最大值与单一孔隙率时的饱和度曲线最大值相近，说明这种流动并不会影响到大孔隙率区域。

但研究尚未对多孔电极孔隙结构进行更加真实的重构。真实情况中，锂离子电池负极石墨材料为片层结构；在三维模型下，电解液在多孔电极中较之二维模型下具有更多的流通通路；电极多孔介质实质应由正负极材料与黏结剂黏合构成。未来将采用新方法对电极三维结构进行重构，并建立三维格子Boltzmann非混相驱替模型，届时，可以分别考虑黏结剂和材料的不同物性对输运的影响。

[1] 罗庆凯, 王志荣, 刘婧婧, 等. 18650型锂离子电池热失控影响因素[J]. 电源技术, 2016, 40(2): 277-279.

LUO Qingkai, WANG Zhirong, LIU Jingjing, et al. Influencing factors of thermal runaway of 18650 lithium ion battery[J]. Chinese Journal of Power Sources, 2016, 40(2): 277-279.

[2] INAMURO T, YOSHINO M, OGINO F. Lattice Boltzmann simulation of flows in a three-dimensional porous structure[J]. International Journal for Numerical Methods in Fluids, 2015, 29(7): 737-748.

[3] LIU H, KANG Q, LEONARDI C R, et al. Multiphase lattice Boltzmann simulations for porous media applications[J]. Computational Geosciences, 2016, 20(4): 777-805.

[4] CHAI Z, HUANG C, SHI B, et al. A comparative study on the lattice Boltzmann models for predicting effective diffusivity of porous media[J]. International Journal of Heat & Mass Transfer, 2016, 98: 687-696.

[5] WANG M, PAN N. Numerical analyses of effective dielectric constant of multiphase microporous media[J]. Journal of Applied Physics, 2007, 101(11): 227-243.

[6] SHAN X, CHEN H. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical Review E Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1993, 47(3): 1815.

[7] 谢驰宇, 张建影, 王沫然. 多相非牛顿流体驱替过程的格子Boltzmann模拟[J]. 计算物理, 2016, 33(2): 147-155.

XIE Chiyu, ZHANG Jianying, WANG Moran. Lattice Boltzmann modeling of non-newtonian multiphase fluid displacement[J]. Chinese Journal of Computational Physics, 2016, 33(2): 147-155.

[8] LI C, ZHANG L, KANG Q, et al. Nanoscale simulation of shale transport properties using the lattice Boltzmann method: Permeability and diffusivity[J]. Sci. Rep., 2015, 5: 8089.

[9] YUAN P, SCHAEFER L. Equations of state in a lattice Boltzmann model[J]. Physics of Fluids, 2006, 18(4): 329.

[10] YU Z. A novel lattice Boltzmann method for direct numerical simulation of multiphase flows[D]. Columbus: The Ohio State University, 2009.

The lattice Boltzmann simulation of electrolyte displacement in battery injection process

YU Tao1, LI Dinggen1, ZHANG Xiaojun2, DAI Kewen2

(1Huazhong University of Science and Technology, Wuhan 430074, Hubei, China;2Liaoning Petroleum Equipment Research Institute Co., Ltd., Panjin 124010, Liaoning, China)

In the process of lithium-ion power battery electrolyte injection, the electrolyte displacement efficiency directly affects the forming quality of the solid electrolyte interface (SEI) in the subsequent process. Microstructure of porous electrode in lithium-ion battery were reconstructed by four random growth parameter method, and an improved pseudo potential lattice Boltzmann model was used to simulate immiscible displacement in battery liquid injection process to investigate the effect of wall wettability and porosity of electrode structure in lithium-ion cell on the displacement efficiency. Research shows that the wetting property of porous electrode has a significant influence on the displacement efficiency. With the increase of contact angle, displacement efficiency decreases. In single porosity zone, with porosity increases, the displacement efficiency is enhanced and less material is left. However, when the electrolyte flows through the interface between the anode and separator, because of difference of wetting characteristics and porosity, the electrolyte shows different displacement efficiency. The higher porosity zone has seepage in the vertical direction of flow, which reduces the displacement efficiency in other side and formed bubbles to affect the formation of SEI.

lattice Bolztmann; pseudo potential model; battery injection; displacement efficiency

10.12028/j.issn.2095-4239.2017.0165

TM 911

A

2095-4239（2018）02-0276-06

2017-11-20；

2017-12-29。

国家科技支撑计划项目（2015BAG17B02）。

俞涛（1992—），男，硕士研究生，从事锂离子动力电池安全问题研究，E-mail：hustyutao92@foxmail.com；

李顶根，博士，副教授，从事锂离子动力电池热失控研究，E-mail：lidinggen@sina.com。