Ford-Fulkerson算法在建设工程项目进度协调中的应用

刘 卿

上海前滩国际商务区投资（集团）有限公司 上海 200126

在目前社会上项目工期紧、劳动力资源紧缺成为普遍现象的大环境下，如何更科学、有效地进行项目进度控制，成为我们需要研究的问题。建筑工程是一项复杂的工程，融合了很多项目管理及管理学的知识体系，不仅要求整个团队有技术及措施，还需要具备相应的管理技巧[1-2]。

解决资源冲突是项目进度管理中的重中之重，这不仅能够使有限资源得到充分运用，同时也能有效控制资源型工期进度。

1 项目概况

前滩某商办项目二期，位于上海市浦东新区前滩地区，总用地面积17 224 m2，总建筑面积130 618.5 m2，地上84 299.7 m2，地下46 318.8 m2，地上建筑为2栋核心筒-钢框架结构高层办公塔楼，以及4栋钢框架结构的商业裙房，整体地下室3层，作为民防工程及地下车库。项目由地面架空钢结构连廊连接塔楼及裙房。其中，办公塔楼地上21层，建筑高度为99.35 m；商业裙楼地上2～3层，建筑高度15.5 m。办公塔楼外立面长55.5 m，宽31.3 m，首层大堂层高5.5 m，2～21层层高4.5 m，屋顶层幕墙檐口高3 m，幕墙顶高98.5 m，各楼层外立面带不规则彩釉图案（图1）。

图1 项目效果图

项目于2014年4月开工，2015年6月完成±0 m节点，2015年12月结构封顶，2016年12月完成幕墙封闭，2017年10月通过各项竣工验收，2018年1月正式交付使用。

2 进度计划及劳动力配置研究

2.1 幕墙施工部署及进度计划

标准层幕墙配置钢化彩釉夹胶中空玻璃，每一层幕墙单元板块数量为124块，2层至屋顶层，共21个作业层，每栋塔楼共计2 604块彩釉单元幕墙。

根据工况要求，2层以上为连续单元幕墙体系，首层大堂采用独立单元幕墙体系，由于大堂需要供大型材料设备进出，故该区域幕墙封闭工作后置，本文不研究其进度协调问题。

根据现场施工方案布置，外立面区域布置大型垂直运输工具，即塔吊、施工电梯，每一层分别影响6块和7块单元不能连续施工，故每一个标准层的施工段可连续施工的单元幕墙为111块，影响范围为2～21层，塔吊区域和施工电梯区域单元板块最晚在屋顶层单元板块吊装之前封闭，分别有120块和140块单元。

根据本项目幕墙加工及安装的工艺流程，按每5个标准层为一个工艺批次，最后塔吊、施工电梯及屋顶层为一个工艺批次。

根据施工部署，需对2栋塔楼依次进行幕墙深化设计和单元板块加工、单元连接件及2层打底框安装、标准层单元板块安装、塔楼口及货梯口单元板块安装封闭、屋顶层单元板块安装。

塔楼幕墙规模如表1所示。

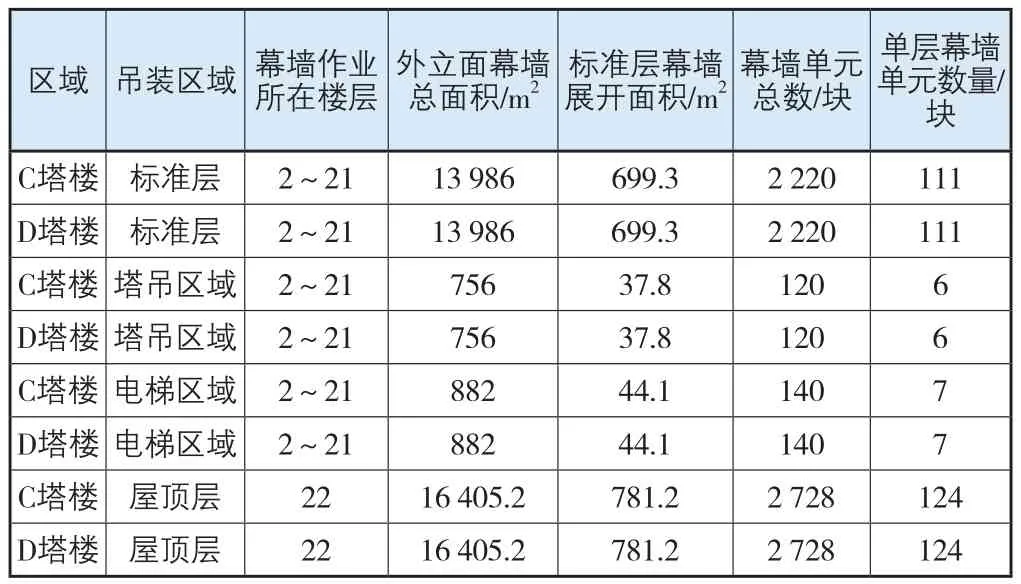
表1 塔楼幕墙单元板块规模

塔吊区、施工电梯区以及最后的屋顶层体量与一个标准层相差无几，该批次约等同于3个标准层的工作，最后形成幕墙吊装的关键工作及工期计划（图2）。

图2 幕墙吊装工期计划

该进度计划中，幕墙加工占据了关键线路，同时为保证2栋塔楼的整体形象进度，2栋塔楼幕墙的加工工作交替进行，吊装工作也交替穿插进行，是非关键线路工作，用时标网络图表述，理论上存在很多自由时差，进度计划有很大的弹性量，在不考虑劳动力投入限制的情况下看似合情合理。

2.2 劳动力资源需求配置研究

依据LD/T 73.4—2008《建设工程劳动定额》[3]：“劳动力定额是总结某一段时期内先进生产方法的手段，通过对施工生产过程的观察、分析综合制定的。它比较科学地反映出生产技术和劳动组织的先进合理程度，所需的资源的前提是满足普遍的平均先进水平，具有相对稳定，并根据生产力的提高逐步完善。”

由于单元板块在工厂自动化流水线加工，故工厂劳动力资源配置不影响项目现场施工进度。本次研究现场安装的劳动力资源限制条件下的进度协调问题，研究其中体量最大、工期持续最长并最具代表性的标准层吊装期间的进度。

在《建设工程劳动定额》中，明框幕墙的基本劳动力需求为每10 m2需求3.511工日，标准层施工的劳动力强度基本投入总量为240工日，根据图2计划，每标准层需要6日安装流水节拍，每标准层幕墙吊装的每日劳动力基本需求为40工。

根据施工工艺，幕墙单元板块现场完成吊装需要2类工种。第1类为运输工，其作用为从地面堆场将单元板块运输至起吊位置，并将单元板块牢靠固定在缆风绳索吊钩上。第2类为包括指挥司号在内的紧密配合吊装的工人，其作用是通过操作顶层滑轨及卷扬机，将单元板块进行垂直起吊并水平移位到工位，并进行一列辅材安装及板块精确就位、矫正、复核、固定等工作。

根据工程特点并参考市场常规取值，考虑施工单位实际的工效时间及成本，控制总劳动力工日投入量常规经验比值为：安装∶运输=6∶1，人数取整=34∶6。

本项目标准层幕墙吊装需要的最大工日为240工日，其中需要运输工36工日，活动持续6 d，则每天需要6人；幕墙安装施工需要安装工204工日，活动持续6 d，则每天需要34人。每个单体需要的2种资源如表2所示。

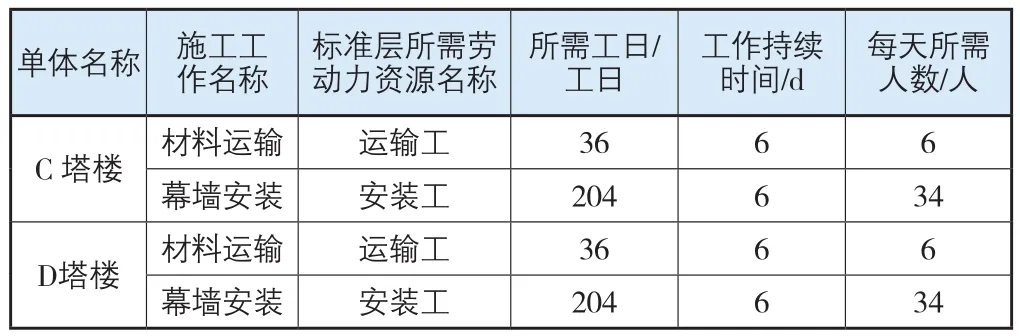
表2 塔楼标准层施工劳动力资源需求

在施工单位投标文件及施工组织设计的现场劳动力计划表中，安装工单日投入最大人数限制为60人，运输工单日投入最大人数限制为10人。在实际项目中，可能因施工单位对项目的理解以及技术、管理水平存在一定差距，故我们有必要对劳动力计划进行校验和复核。

3 劳动力资源限制复核

我们采用“最大流问题”对每项资源的投入进行复核研究，首先研究2个单体标准层平行施工时各工序工作的劳动力问题。

3.1 标准层安装工

任一个单体工程的标准层幕墙安装工在每天内投入不超过34工，完成此项工作均需204个工日，2个单体劳动力限制共60人，求解能否在6 d内如期完成。

依据上述建立模型方程：

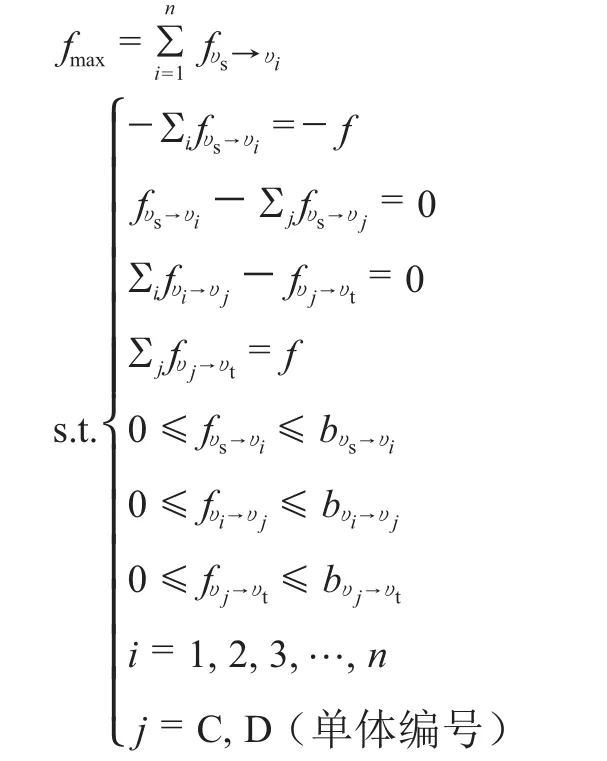
方程中υs节点表示起点，υt节点表示终点；υi（i=1～m）分别表示发生在第1天、第2天、第3天、…、第n天（n为计划工期）的工作，从υs到υi弧的流量表示为所投入在第i天针对所有单体的劳动力当天人数，记为，每天所有单体劳动力最大限制数记为，且应满足。

υj（j=C、D）表示第i天完成 j单体的工作状态，从υi到υj弧的流量表示第i天在j单体工作上所投入的当天劳动人数，记为，每天j单体的劳动力最大投入数记为，且应满足。

从υj到υt弧的流量表示j单体在第1天至第n天累计的工日数，记为，而根据前文劳动力资源需求配置，j单体此项工作完成任务需要的总工日数记为，且应满足。

根据以上分析，将工程用计划网络图表示（图3）。

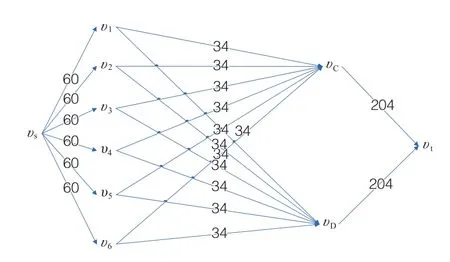
图3 标准层幕墙安装6 d最大流网络图

根据数学模型，我们要研究在不超过劳动力限制条件下，现有的劳动力计划能否保证工期的问题，我们采用福德-富克逊算法[4]进行计算，其中：bυs→υi=60，bυi→υj=34，bυj→υt=204。

先为网络分配一个任意初始流，除υs及υt节点，每个节点流入和与流出和一致，标在图中弧旁的括号内（图4）。

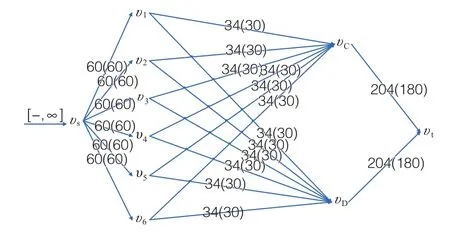
图4 标准层幕墙安装6天最大可行流网络图

为υs标记[－,∞]，S={υs}，S={υ1,υ2,υ3,υ4,υ5,υ6,υC,υD}，可以得出，从S到S的 正向弧都是饱和弧，且逆向弧都是零流弧，因此S中 的点均不可标记，所以，当前可行流是最大流，且不存在增广链。

最小割集为：{(υs,υ1), (υs,υ2), (υs,υ3), (υs,υ4),(υs,υ5), (υs,υ6)}，最大流量fmax=最小割集容量=360。

我们得到2个单体标准层幕墙吊装工作平行施工，在6 d内的每日劳动力分配结果。从网络图中我们发现，fυC→υt，fυD→υt均未全部达到其最大流量204，其意义就是所投入的劳动力无法全部完成应有的任务，要增加工作天数。

设工作天数为7 d，并重新进行复核计算。通过迭代，在满足的前提下，我们得出一个最大可行流网络图（图5），并得出劳动力分配的可行解（表3）。所得的结果反映了2个单体的施工同步进行，按现有的劳动力资源限制及劳动力投入，至少需要7 d能将一个标准层的工作全部完成。如若标准层幕墙吊装工作持续7 d，每天劳动力投入量可以低于60人的限制数。

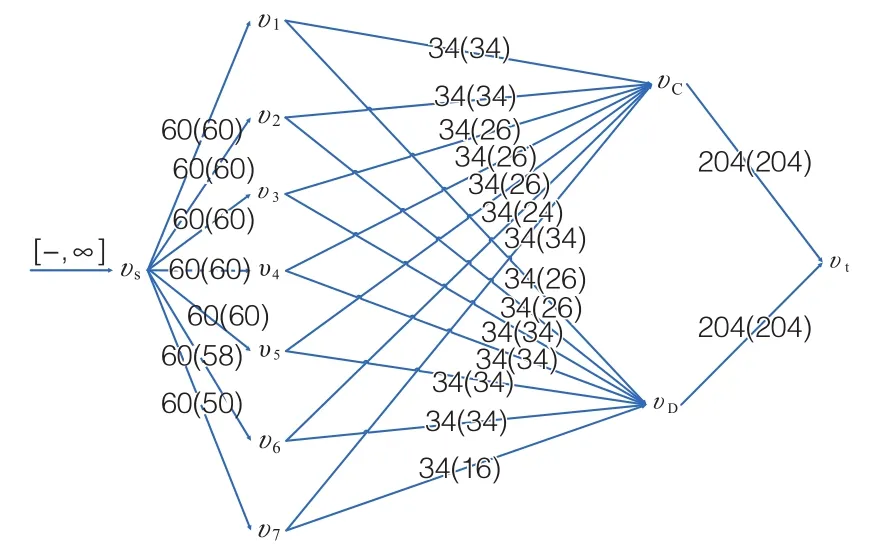
图5 标准层幕墙安装7 d最大可行流网络图（安装工）

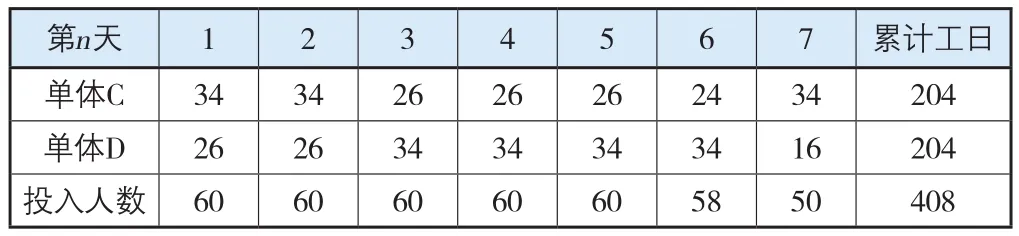
表3 标准层幕墙安装工7 d工期劳动力分配可行解

利用福德-富克逊算法也可以反推试算每天投入人数上限的最低值：

1）设人数限制为59，即：bυs→υi=59，bυi→υj=34，bυj→υt=204。得出劳动力分配结果（具体验算过程同上文），如表4所示。

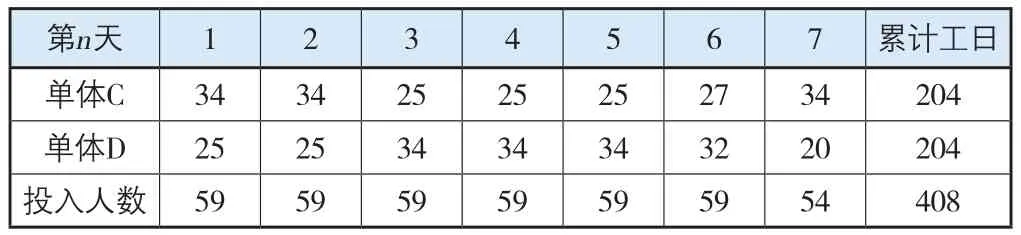
表4 安装工59人限制的7 d工期劳动力分配可行解

2）设人数限制为58，即：bυs→υi=58，bυi→υj=34，bυj→υt=204。得出劳动力分配结果可行解，如表5所示。

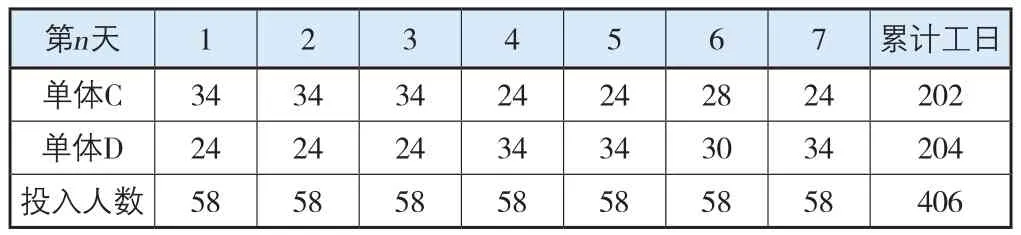
表5 安装工58人限制的7 d工期劳动力分配可行解

存在fυj→υt＜bυj→υt且Σjfυj→υt=406，说明已突破59人的最低限制。

3.2 标准层运输工

任一个单体工程的标准层运输工在每天内投入不超过6工，完成此项工作均需36个工日，2个单体劳动力限制共10人，考虑资源比重比较大的安装工程持续了7 d，先求解能否在7 d内如期完成。

通过验算，对各单体标准层运输工进行复核，bυs→υi=10，bυi→υj=6，bυj→υt=36，通过迭代，我们得出一个7 d工期前提下的最大可行流网络图（图6）。可知fmax=70＜72，且fυD→υt=34，未达到其最大流量36，我们可以得出人工的投入量略微不足，解决措施是要么再延长1 d工期，要么提高劳动效率。

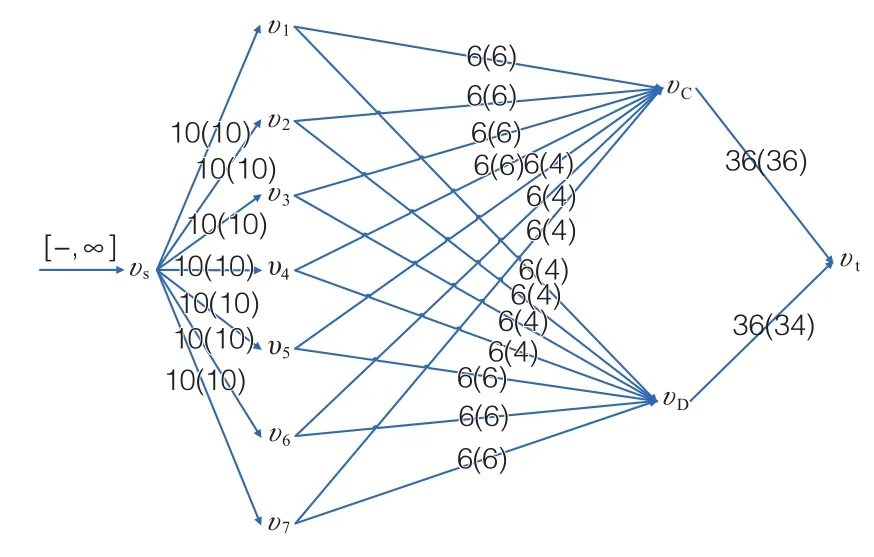
图6 标准层幕墙安装7 d最大可行流网络图（运输工）

因为fυD→υt仅仅与最大流量相差2个工日，假设每天增加1个劳动力配置上限数量，通过福德-富克逊算法，对各单体标准层运输工再次复核，bυs→υi=11，bυi→υj=6，bυj→υt=36，得出运输工的工期及劳动力分配结果，就明显可以满足7 d的工期需求（表6）。也可以得出一个定论，如果提高运输工作10%的效率，也能满足现有10个运输工限制条件下7 d的施工任务。

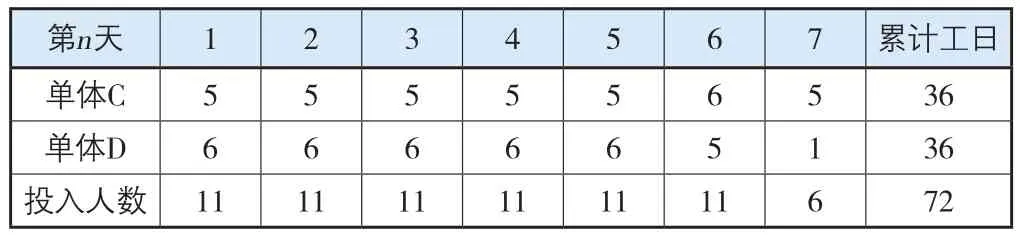
表6 运输工11人限制的7 d工期劳动力分配可行解

通过对劳动力资源限制的复核，在当前2种工种的劳动力限制的条件下，2个单体平行施工时，不能在6 d计划工期内全部完成。首先，安装工及运输工作需要分别采用延长工种时长。其次，如按7 d的工期，安装工投入量则相对比原计划多，对决策者而言，可以视具体情况对存缺口的工种进行岗位调剂。当然，另外一点说明原有工期计划没有充分考虑劳动力资源的协调问题，资源限制会对工期计划产生影响。

4 资源限制型进度对比及调整优化

原进度计划（见图2）通过与Microsoft Project 2016软件资源—工期优化功能进行相比，在Project甘特图的对应任务中分配资源，并在资源分配表设置劳动力上限，再用软件检查劳动力超限，最后进行软件资源分层优化，得出Project软件优化之后的进度计划，显然进度还延后了半个月（图7）。

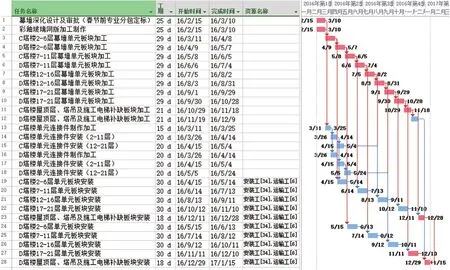
图7 Project软件资源—工期优化横道图

由于现场劳动力投入是一个相对固定值，如果劳动力分配不均，必然会出现劳动力瓶颈，很大程度上会影响实际工作推进，如果非关键线路的工作延迟时间大于自由时差，一定程度上又会转换成关键线路，最后影响总工期，该计划并未考虑幕墙工艺样板施工及整改复核的时间。

通过前文的劳动力复核，我们得出在2个单体平行施工的最不利条件下，每天的劳动力需求都是一个比较均衡并紧凑连续的进程，充分发挥了劳动力的效率。

平行施工的每一批次每一标准层每天的劳动人数按照表4及表6所得的可行解投入，我们发现在前道工序的工作面及材料供应及时的前提下，2个工种每天的投入量没有存在任何超限情况，劳动力总数不变，进度节点有保障，且从项目决策层角度出发，更注重前期的工艺样板的复核确认，通过优化我们得到了更切实际、也更经济有效的项目进度计划（图8）。

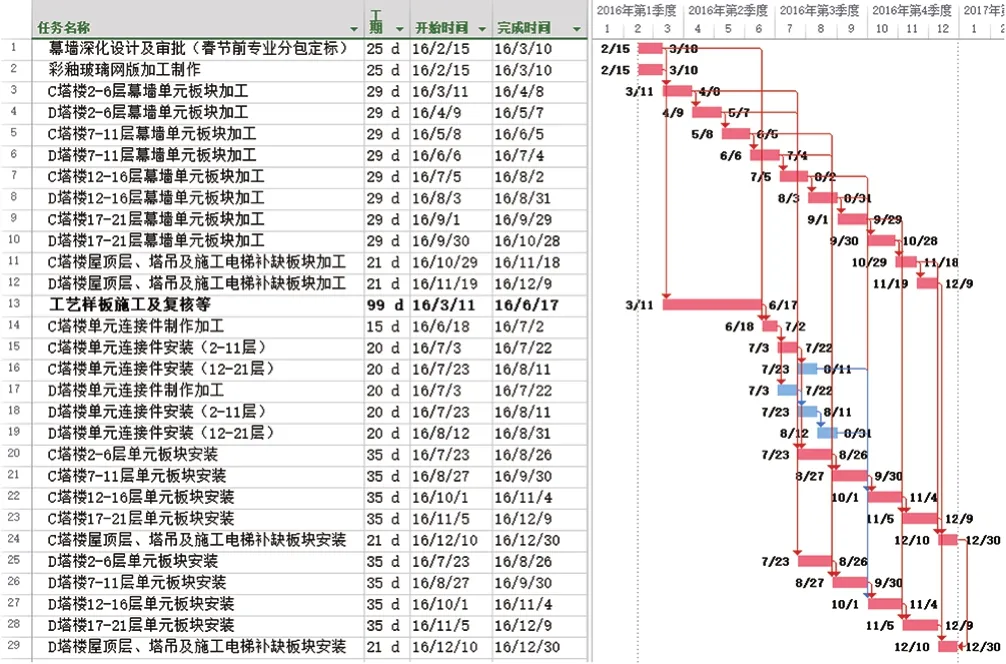
图8 结合最大流算法的资源—工期优化横道图

5 结语

在多任务平行施工的状态下，势必会受到不同劳动力资源限制。因为有工期要求，不能随意延长工期，但一旦出现劳动力瓶颈，就必须得调整计划以满足资源限制，并力求影响最小值。

受篇幅及研究所限，本文所得出的结果未能详尽及充分地体现出其对整个项目起到的作用有多大，还值得更深层次的研究。但采用最大流的数学计算模型，能够有效地解决在工期相对紧张、所需资源受到投入限制条件下，多单体同时施工时的劳动力资源分配问题，相对于当前一些学术理论的计算方法，该模型更加直观、有效地阐述劳动力分配的过程[5-10]，更值得项目精细化管理借鉴。研究的内容也可为地产开发企业在当前经济背景及普遍资源限制环境下进行进度控制工作提供借鉴，具有时代特点和现实意义。