基于 Sobol’法的轨道车辆平稳性的全局灵敏度分析

邵永生，李成，成明

(苏州大学 轨道交通学院，江苏 苏州 215131)

高铁作为一种快捷、安全的交通方式，近十多年来发展迅速，技术日趋成熟，行车安全和速度都已得到较好保障，人们乘车时开始更多关注舒适度和平稳性等运行品质。各国评价运行品质的标准不同，如欧洲的E. Sperling指标、日本的舒适度系数和英国的乘坐指数等。其中Sperling平稳性指标在国际上得到广泛认可和应用，故本文采用 Sperling指标作为车辆运行平稳性的评价指标。乘车舒适度受车辆运行过程中产生的各种振动影响，车辆振动的大小不仅与线路质量有关，还和车辆走行部分的结构参数有关。不同的参数变化对平稳性的影响不同，参数的不确定性所引起的结构响应的不确定性程度称为随机参数的灵敏度[1]。参数灵敏度分析方法分局部灵敏度分析法和全局灵敏度分析法2种。局部灵敏度分析方法[2−3]主要有直接求导法、格林函数法和有限差分法，局部法应用范围有限，不能考虑参数分布的影响，主要应用于微分方程较易推出、线性或者非线性较弱的系统。全局灵敏度分析方法主要有Sobol’法、Morris法和傅里叶幅值检验扩展法等。全局灵敏度分析[4]较之于局部灵敏度分析，参数的变动范围可以扩展到整个定义域，不仅能考虑参数的概率分布，而且各个参数可以同时变化，从而可以考虑到各个参数之间的交互作用。其中Sobol’法作为经典的全局灵敏度分析方法，与其他全局灵敏度分析法相比，它能采用与计算一阶灵敏度类似的方法快速简便地计算出高阶交叉影响项[5]，已广泛应用在航空、武器、汽车等领域。刘鑫等[6]基于 Sobol’法对人体不同部位角度对人体头颈部损伤响应的影响进行了灵敏度分析，结果表明，人体头颈部角度和体位角对人体损伤响应有着重要影响；WAN等[7]采用Sobol’法对洪水预报模型的4个不同目标函数进行灵敏度分析，为研究更复杂的水文模型奠定了基础；于德介等[8]将 Sobol’法引用到结构动力分析中，得出了软、硬弹簧和线性阻尼对传递率的影响规律，其结果为系统的优化设计提供了依据。然而，目前尚未有Sobol’法应用于轨道车辆平稳性分析的研究报道。鉴于Sobol’法的分析优势，本文将Sobol’法引入到轨道车辆平稳性的灵敏度分析中。首先基于轨道车辆垂向模型，采用虚拟激励法和三角级数反演理论求解Sperling指标；建立Sperling指标与各参数间的关系，并通过Sobol序列对影响平稳性的11个参数随机采样；然后分析车辆垂向模型平稳性的灵敏度，得到Sperling指标关于各参数的一阶灵敏度及总灵敏度；最后选取车体质量和一系悬挂刚度作为目标参数进行优化分析。筛选出影响车辆平稳性的主要参数，摒弃影响较小的参数，从而减少后续参数优化的工作量，为优化车辆系统模型参数提供参考。

1　Sobol’灵敏度分析方法

Sobol’法最早于1993年提出，是一种基于方差的蒙特卡洛法[9−10]，其基本思想是将函数 f(y)分解成2n个递增项之和，通过对模型参数采样，计算出模型输出响应的各项偏方差和总方差，从而求得各阶灵敏度。当 n维单元体的参数域为 In时， In=将函数 f(y)分解为2n个递增项之和，具体表达如下：

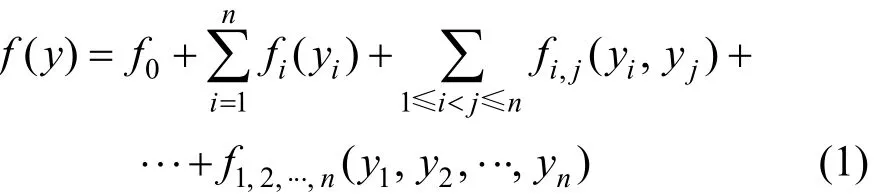
f0为常量，各子项对其所包含任意变量的积分为0，即

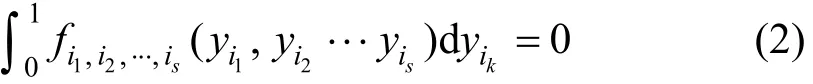
其中：k=1, 2, …, s，由式(1)～(2)可知，式(1)中的所有加数项之间都是正交的且可以表示为函数 f (y)的积分：

由此类推，即可求出式(1)中的其他高阶项。将式(1)的左右两边分别在整个参数域 In内平方并积分，结合式(2)得到

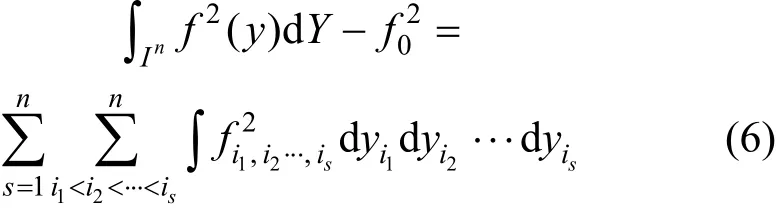
则总方差为

偏方差为

由式(6)可知

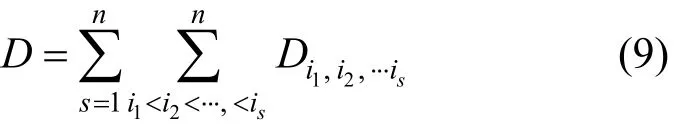
最后得到各阶灵敏度指数

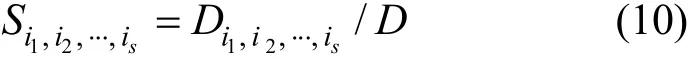
针对车辆垂向模型的平稳性问题，上式中，Sim为第im个参数的一阶灵敏度，反映的是第im个参数单独变化时对平稳性的影响。相应地，Sim,in为一个二阶全局灵敏度系数，反映的是第im个和第in个参数同时变化时对平稳性的影响。以此类推，总灵敏度值为该参数的各阶灵敏度值之和，不但反映了参数单独变化时的作用，还包含该参数与其他参数交互作用的影响[5]。故当某一参数的一阶灵敏度和总灵敏度值相差较大时，即可认为该参数与其他参数之间存在明显的交互作用。

2　轨道车辆垂向模型

建立如图1所示的轨道车辆垂向模型，该模型简化成一个以速度v在轨道上运行的10自由度多刚体系统[11]。

模型由车体、2个转向架和4个车轮组成，其中，Mc，Mt和Mw分别是车体、转向架、车轮的质量，Jc和Jt为车体和前后转向架的转动惯量，K1，K2，C1和 C2分别是一系悬挂和二系悬挂的弹簧刚度和阻尼系数。lc和 lt是车辆定距之半和转向架轴距之半。垂向模型中，总共考虑车辆系统的 10个自由度，分别是：车体的垂向位移Zc和转角θc，前转向架的垂向位移 Zt1和转角θt1，后转向架的垂向位移Zt2和转角θt2，4个轮对的垂向位移Zw1，Zw2，Zw3和 Zw4。

图1　车辆垂向模型示意图Fig. 1　Sketch of vertical model for railway vehicle

运用达朗贝尔原理，分别得到车体浮沉和点头运动、前后转向架浮沉和点头运动、4个轮对点头运动的振动微分方程，联立方程，得到其矩阵形式为

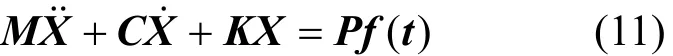
其中：M，C和K是系统的质量、阻尼和刚度矩阵；X 是系统的虚拟位移响应向量是输入激励矩阵；f (t)是不平顺位移激励向量其中为激励时延，v是车辆行驶速度。

3　基于虚拟激励法的Sperling平稳性指标

虚拟激励法[12−13]较之于传统的随机振动方法，其最大优点在于计算时使随机激励下随机结构振动响应的“双随机问题”转换成“单随机问题”，使得计算工作量大为减少。基于第2节所建立的轨道车辆模型，可以认为任意二车轮均受到来自于轮轨的相同随机激励，但其间存在一个时间差。

假设系统受到4点异相位平稳随机激励 f (t)

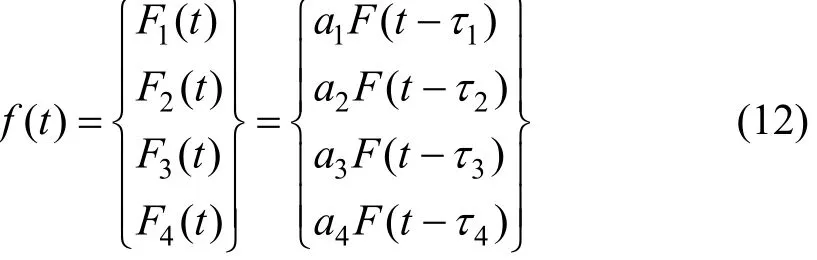
其中：F(t)是轨道随机不平顺的时间历程函数；ai(i=1，2，3，4)代表各点的作用强度，由于 4个轮对输入点的强度一样，故令ai=1，则相应的虚拟激励为

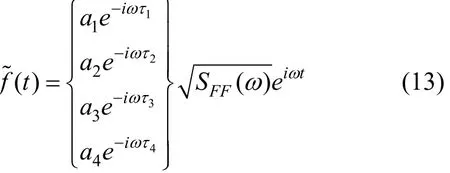
SFF(ω)为 F(t)的自谱密度，将式(13)代入式(11)，得到系统虚拟位移响应

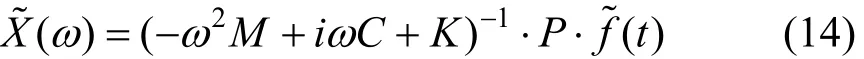
然后分别得到系统位移响应的功率谱矩阵SXX(ω)和垂向加速度功率谱密度矩阵 SX˙X˙(ω)为

根据式(16)求得的系统垂向加速度功率谱密度矩阵 SX˙X˙(ω)，将车体的垂向加速度功率谱密度记为 SX˙X˙(ω,1)。依据三角级数反演理论，采样频率ω处的振动加速度为

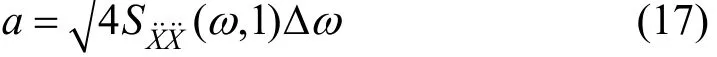
式中：Δω为采样频率间隔。令ω=2πf，将加速度a代入Sperling公式，则频率f 处的平稳性指标为

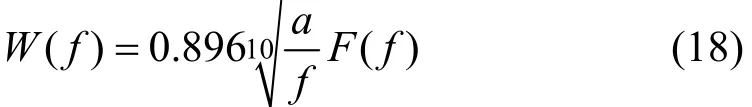
F ( f )是与频率有关的修正系数

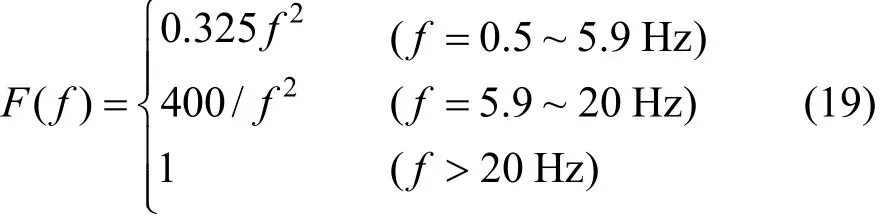
由于车辆振动是随机的，加速度和频率都会随时间的变化而变化，因此需要将频率分组，统计出每个频段下的平稳性的指标，然后得到整个频段下的Sperling指标为

表1　HSC车辆模型参数Table 1　Parameters of HSC vehicle model

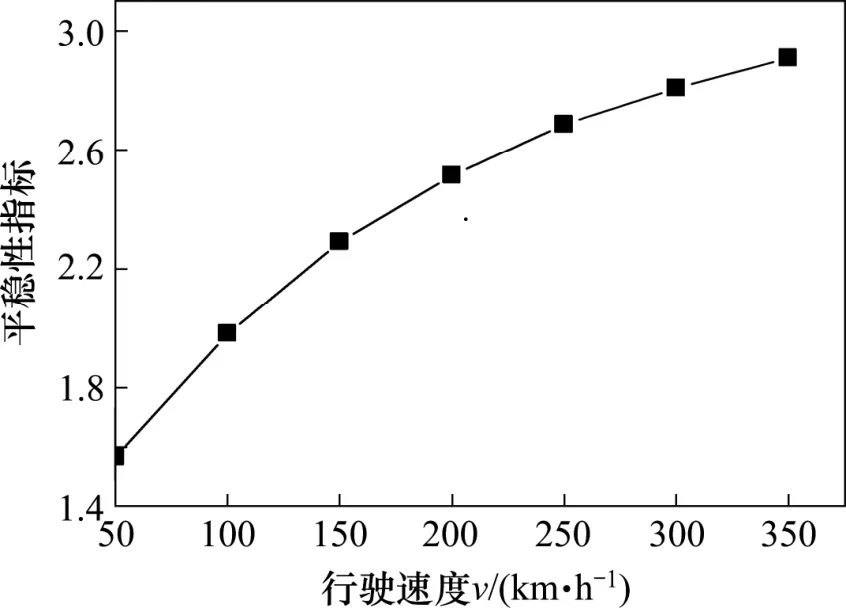
图2　不同速度下的Sperling指标Fig. 2　Sperling index versus speed

采用高速车辆HSC的模型参数(见表1)，运用虚拟激励法求得不同速度下的Sperling指标，如图2所示。可以看出，Sperling指标和列车运行速度呈正相关关系，且随着列车速度的提高，Sperling指标的增幅趋于平缓。例如，当列车速度从50 km/h增加到200 km/h时，平稳性指标增大60.56%；当列车速度从200 km/h增加到350 km/h时，平稳性指标增大15.71%。这就表明，当高铁速度进一步提升时(比如高于250 km/h)，由于列车速度提高所导致的乘车舒适度降低程度有所减缓。

4　数值算例分析

4.1　灵敏度分析

采用Sobol’法进行灵敏度分析前，应先给定参数的变化区间及概率分布，本文以Sperling指标为目标函数，选取德国高速低干扰轨道谱作为轨道不平顺输入激励，对影响Sperling指标的11个参数进行分析，假定各个参数分布均匀，所选各个参数分布范围见表2。

根据表2，采用Sobol序列对各个参数随机采样。Sobol序列为低差异序列，属于拟蒙特卡罗法，但与传统蒙特卡罗法比较，它采样更均匀，可以扩展到任意维度，是一个稳定的、覆盖率非常好的序列[14−15]。设定采样的样本量N=2 000，采用Sobol’法分别计算了低速(v=50 km/h)、中速(v=200 km/h)和高速(v=350 km/h)3种情况下车辆模型参数对Sperling指标的一阶灵敏度和总灵敏度，如图 3所示。

图3中横坐标1～11代表车辆模型的11个参数，分别是车体质量、转向架质量、车轮质量；车体和前后转向架的转动惯量；一系悬挂弹簧和悬挂阻尼、二系悬挂刚度和悬挂阻尼；车辆定距之半和转向架轴距之半。

表2　车辆模型参数分布范围Table 2　Range of vehicle model parameters

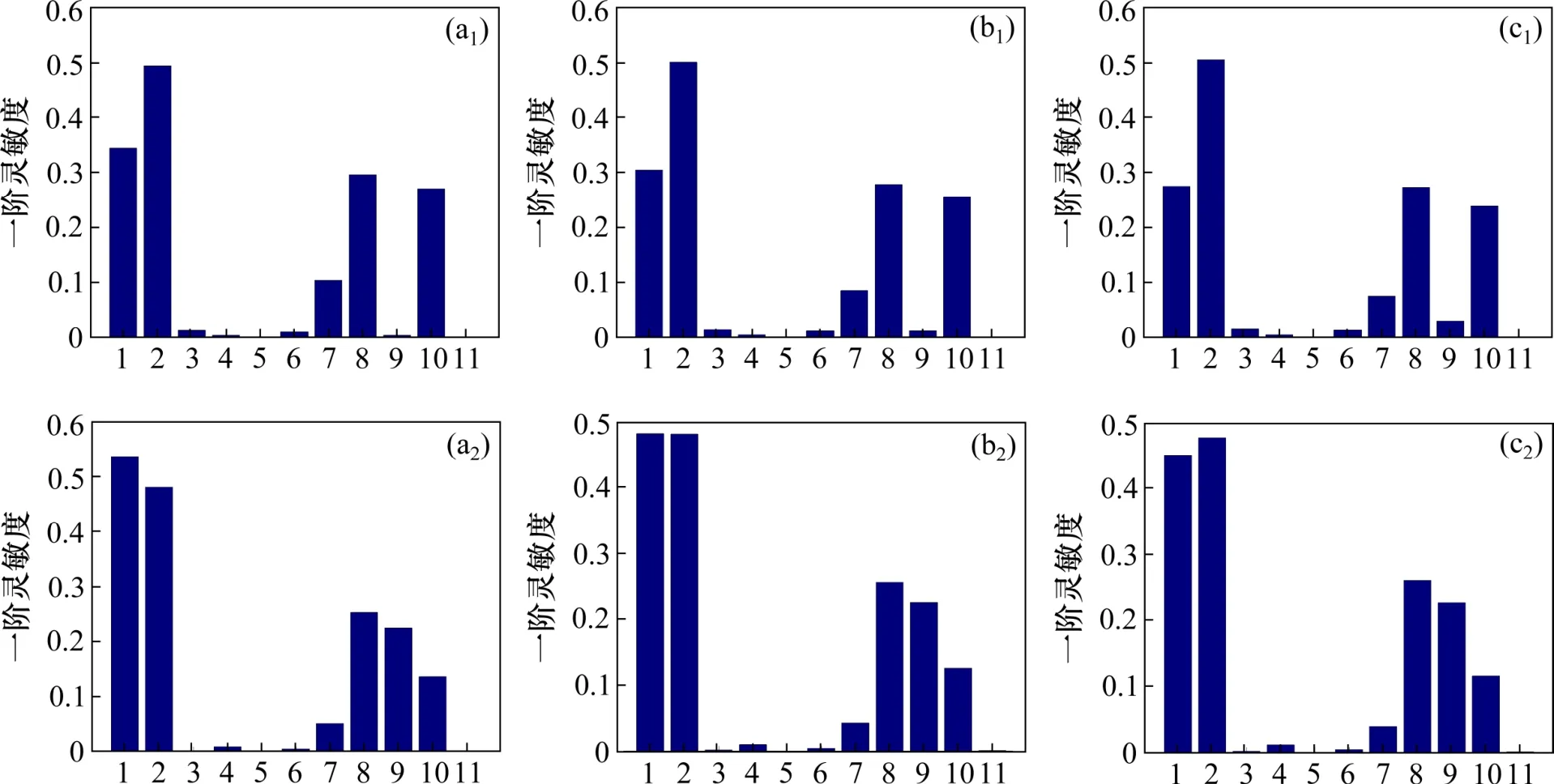
图3　不同速度下的一阶灵敏度及总灵敏度Fig. 3　First order sensitivity and total sensitivity with respect to speed

从图3可以看出，低速时车体质量的总灵敏度值大于构架质量的总灵敏度值，说明在各参数交互耦合作用下，车体质量对Sperling指标的影响程度高于构架质量对Sperling指标的影响程度。然而随着列车速度的提高，车体质量对Sperling指标的影响程度逐渐小于构架，这说明列车速度的提高，逆转了相关参数在列车平稳性中的重要性。总的来说，3种速度下的灵敏度图只是略有差异但相差不大，这说明Sperling指标的主要影响因素受速度改变的影响相对较小。

不考虑交互作用时，车体质量对Sperling指标的影响最大，其次是转向架质量、二系悬挂刚度、车辆定距之半和一系悬挂阻尼。考虑参数间交互作用时，车体质量和转向架质量对Sperling指标的影响都很大，其次是二系悬挂刚度、二系悬挂阻尼和车辆定距之半。转向架点头惯量与转向架轴距之半的一阶灵敏度和总灵敏度都很小，说明这2个参数对平稳性的影响可忽略不计。车体质量和二系悬挂阻尼的一阶灵敏度值和总灵敏度值相差较大，表明这2个参数与其他参数之间存在明显的交互作用。为了与已有文献结果进行对比，仅在车辆模型的一、二系悬挂参数中进行比较，发现对Sperling指标影响最大的是二系悬挂刚度，这与文献[2]的结论一致，说明Sobol’法应用在轨道车辆平稳性灵敏度分析中是可行的。

4.2　参数优化及讨论

从以上全局灵敏度分析结果可以看出，车体质量对平稳性影响较大，一系悬挂刚度对平稳性影响较小。因此，本节以这2个具有代表性的参数为目标参数进行优化对比分析。以速度v=350 km/h的高速车辆模型为例，假定其他参数为固定参数，考虑各个参数的交互作用，分别求出车体质量和一系悬挂刚度在定义域范围内的Sperling平稳性指标如图4和图5所示。

图4　平稳性指标与车体质量关系图Fig. 4　Relationship between ride quality index and vehicle mass

从图4和图5可以看出，平稳性指标和车体质量呈负相关关系，和一系悬挂刚度呈正相关关系。考虑到平稳性指标越大，平稳性能越差，因此，为了提高列车运行平稳性，优化模型参数时，可以采取提高车体质量，降低一系悬挂刚度的途径。此外，平稳性指标在车体质量定义域内变化了 0.122，在一系悬挂刚度定义域内变化了 0.006，这表明车体质量变化对平稳性的影响大于一系悬挂刚度变化对平稳性的影响，与灵敏度分析得到的结果吻合，进一步验证了Sobol’法应用在轨道车辆平稳性灵敏度分析中的准确性。

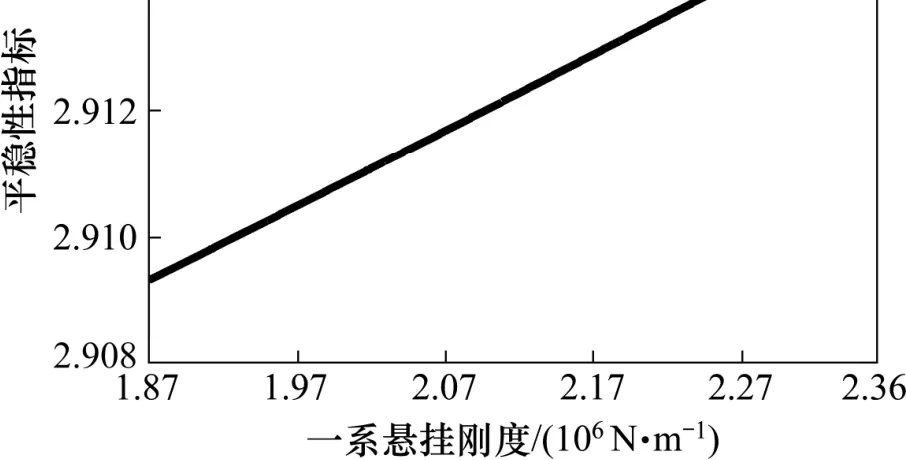
图5　平稳性指标与一系悬挂刚度关系图Fig. 5　Relationship between ride quality index and the first suspension stiffness

5　结论

1) 列车速度和运行平稳性呈负相关关系，但随着速度进一步提升，平稳性降低程度有所减缓；车体质量、转向架质量、二系悬挂刚度和车辆定距之半对Sperling平稳性指标影响较大；转向架点头惯量与转向架轴距之半对平稳性影响较小；车体质量和二系悬挂阻尼与其他参数交互作用明显；平稳性指标和车体质量及一系悬挂刚度分别呈负相关和正相关关系。

2) 相比于局部灵敏度分析方法，Sobol’法不仅允许所有参数共同变化且变动范围可扩展到整个定义域，而且考虑了各参数之间的交互作用，更深入地分析了各个参数对平稳性的影响。

3) 通过 Sobol’法对轨道车辆模型平稳性进行全局灵敏度分析，甄选出影响车辆平稳性的部分重要参数，减少参数优化工作，提高优化效率，为车辆模型设计和参数优化提供理论依据。

参考文献：

[1] 李双, 余衍然, 李成, 等. 随机悬挂参数下轨道车辆平稳性的全局灵敏度分析[J]. 铁道学报, 2015, 37(8):29−35.LI Shuang, YU Yanran, LI Cheng, et al. Global sensitivity analysis on the ride quality of railway vehicle with stochastic suspension parameters[J]. Journal of the China Railway Society, 2015, 37(8): 29−35.

[2] 韩林山, 李向阳, 严大考. 浅析灵敏度分析的几种数学方法[J]. 中国水运(下半月), 2008, 8(4): 177−178.HAN Linshan, LI Xiangyang, YAN Dakao. Analysis of the sensitivity analysis of several mathematical methods[J]. Journal of China Water Transport, 2008, 8(4):177−178.

[3] 张保, 孙秦. 结构特征值灵敏度的半解析伴随变量法[J]. 机械科学与技术, 2013, 32(8): 1221−1224.ZHANG Bao, SUN Qin. The semi-analytical adjoint variable method of structural eigenvalue sensitivity[J].Mechanical Science and Technology for Aerospace Engineering, 2013, 32(8): 1221−1224.

[4] Chu Y, Hahn J. Global sensitivity analysis[J].Encyclopedia of Systems Biology, 2013, 43(6): 841−842.

[5]聂祚兴, 于德介, 李蓉, 等. 基于 Sobol’法的车身噪声传递函数全局灵敏度分析[J]. 中国机械工程, 2012,23(14): 119−123.NIE Zuoxing, YU Dejie, LI Rong, et al. Global sensitivity analysis of auto bodies’ noise transfer functions based on Sobol' method[J]. China Mechanical Engineering, 2012, 23(14): 119−123.

[6] 刘鑫, 张志勇, 刘桂萍. 基于Sobol法的载人空降人体头-颈部损伤响应特性研究[J]. 振动与冲击, 2012,31(14): 133−136.LIU Xin, ZHANG Zhiyong, LIU Guiping. Characteristics of human head-neck injury response to manned airdrop based on Sobol method[J]. Journal of Vibration and Shock, 2012, 31(14): 133−136.

[7] WAN H, XIA J, ZHANG L, et al. Sensitivity and interaction analysis based on Sobol’ method and its application in a distributed flood forecasting model[J].Water, 2015, 7(6): 2924−2951.

[8] 于德介, 李睿. Sobol’法在非线性隔振系统灵敏度分析中的应用研究[J]. 振动工程学报, 2004, 17(2): 210−213.YU Dejie, LI Rui. Application of Sobol’ method in sensitivity analysis of nonlinear vibration isolation system[J]. Journal of Vibration Engineering, 2004, 17(2):210−213.

[9] Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J].Mathematics and Computers in Simulation, 2001, 55(1):271−280.

[10] Korayem M H, Taheri M, Rastegar Z. Sobol method application in sensitivity analysis of LuGre friction model during 2D manipulation[J]. Scientia Iranica, 2014, 21(4):1461−1469.

[11] 孟建军, 杨泽青, 蒲光华, 等. 基于虚拟激励法的轨道车辆垂向振动响应分析[J]. 中国铁道科学, 2012, 33(2):89−94.MENG Jianjun, YANG Zeqing, PU Guanghua, et al.Analysis of vertical vibration response of railway vehicle based on pseudo-excitation method[J]. Journal of China Railway Science, 2012, 33(2): 89−94.

[12] WANG Y, WANG S, HUANG L. Random vibration analysis for impellers of centrifugal compressors through the pseudo-excitation method[J]. International Journal of Computational Methods, 2015, 12(4): 1−16.

[13] 孙建梅, 叶继红, 程文瀼, 等. 考虑空间相干的虚拟激励法在大跨度空间结构随机振动分析中的应用[J]. 铁道科学与工程学报, 2007, 4(5): 11−21.SUN Jianmei, YE Jihong, CHENG Wenrang, et al.Application of the pseudo-excitation method with spatial coherence in random vibration analysis of long apan apace structures[J]. Journal of Railway Science and Engineering, 2007, 4(5): 11−21.

[14] CHEN W, YAN H, PEI X, et al. A Quasi Monte Carlo probabilistic load flow method of distribution system containing distributed generation and electric vehicle charging load based on Sobol sequence[C]// Electricity Distribution(CICED),2016ChinaInternational Conference on IEEE, 2016: 1−7.

[15] 万华平, 任伟新, 王宁波. 高斯过程模型的全局灵敏度分析的参数选择及采样方法[J]. 振动工程学报, 2015,28(5): 1−7.WAN Huaping, REN Weixin, WANG Ningbo. A Gaussian process model based global sensitivity analysis approach for parameter selection and sampling methods[J]. Journal of Vibration Engineering, 2015,28(5): 1−7.