阿志河悬索桥塔梁纵向连接方式与参数分析
刘 鑫,王小松,但莎琦
(重庆交通大学 土木工程学院,重庆 400074)
大跨径悬索桥在活载、纵向静阵风、地震荷载等不对称荷载作用下,加劲梁梁端和索塔塔顶会产生纵向水平位移[1-2]。随着交通流量的增大,根据JTJ 021—89《公路桥涵设计通用规范》[3]设计的悬索桥可能出现塔梁相对位移和塔顶水平位移过大的现象,造成支座、伸缩缝破坏等病害。为研究大跨径悬索桥合理的塔、梁纵向加固方式,本文以阿志河大桥为工程背景,基于JTG D60—2015《公路桥涵设计通用规范》[4]开展漂浮体系大跨径悬索桥采用弹性约束体系和限位约束体系在不同荷载工况下的桥梁静力学和动力学分析。
1 工程概况
阿志河大桥位于六盘水市境内,是一座预应力混凝土加劲梁悬索桥(见图1),主缆计算矢跨比1/9。主缆跨径布置为镇宁岸75 m(无吊索)、主跨283 m和水城岸90 m(无吊索)。主缆中心距为14 m,吊索间距为5 m(近塔吊索距塔中心线6.5 m)。大桥设计车辆荷载为汽车-超20级,挂车-120,桥址区地震烈度属Ⅵ度。本文采用通用有限元软件MIDAS/Civil建立阿志河大桥全桥有限元模型,对索塔与主梁间的连接体系进行模拟分析。
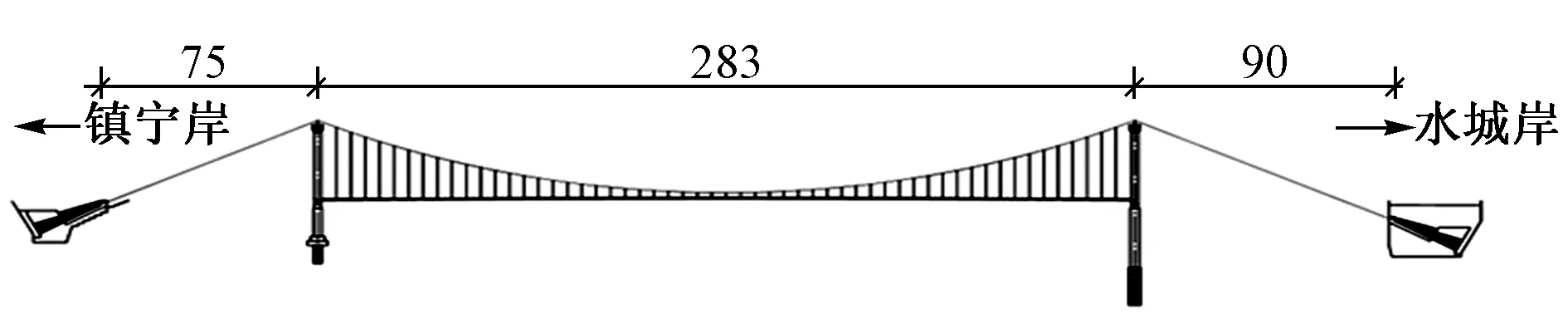
图1 阿志河大桥立面(单位:m)
2 弹性约束体系
为了减小静力反应和地震反应作用下主桥产生过大的梁端位移,在主塔横梁和主梁之间设置弹性索,形成弹性约束体系[5]。采用弹性约束体系进行静动力分析时,弹性索的刚度取值对悬索桥结构内力、梁端位移以及整体抗震性能的影响很大。不同弹性刚度时,结构在静力作用下和地震作用下的桥梁响应分别见图2 和图3。
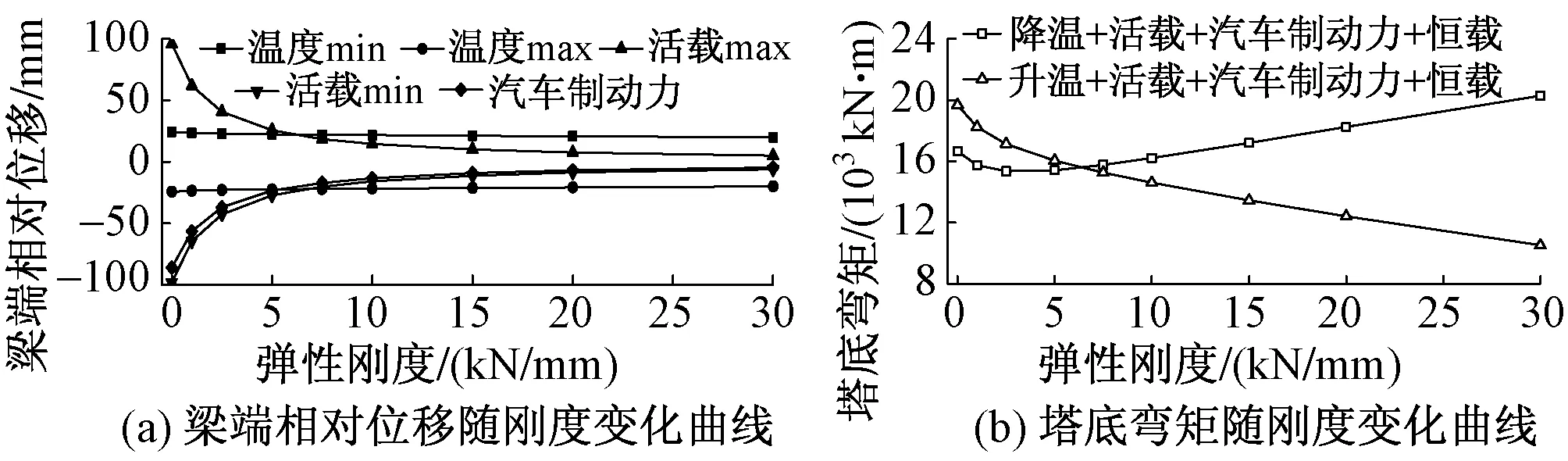
图2 不同弹性约束刚度下的桥梁响应(静力作用下)
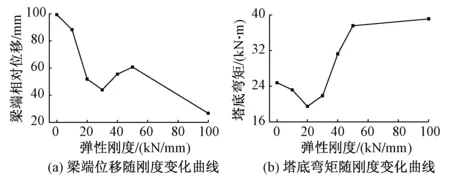
图3 不同弹性约束刚度下的桥梁响应(地震作用下)
由图2和图3可知:
1)随着塔梁弹性约束刚度的增大,塔梁相对位移在静力和地震作用下总体呈现减小的趋势。当弹性刚度为0~10 kN/mm时,塔梁相对位移在各项静力作用下变化比较明显,达到10 kN/mm后,逐渐趋于稳定。当弹性刚度达到100 kN/mm时,地震作用下塔梁相对位移减幅达73%。
2)升温与其他静力荷载工况组合作用有利于塔底受力,塔底弯矩随塔梁弹性刚度的增大而减小。当弹性刚度达到30 kN/mm时,塔底弯矩减幅达47%;在降温与其他静力荷载工况组合作用下,塔底弯矩随塔梁弹性约束刚度的增大而增加,弹性刚度在5 kN/mm左右塔底弯矩出现最小值。在地震作用下,弹性刚度达到50 kN/mm后,塔底弯矩变化趋于平稳,在20 kN/mm左右,塔底弯矩出现最小值。
根据分析结果可知,主塔横梁和主梁之间的弹性索刚度取15 kN/mm时,不仅可以减小塔梁相对位移,而且可以兼顾索塔受力。
3 阻尼限位约束
阻尼限位约束体系为动力阻尼和额定行程量的弹性限位组合的结构体系。考虑到2个索塔与主梁之间相对运动的非同步性,结合主梁与索塔横梁的构造形式,在镇宁岸及水城岸主梁端部与索塔横梁处纵向布置2个限位阻尼器(全桥共计4个)。
3.1 限位阻尼器额定行程(初始间隙)的确定
限位阻尼器的额定行程是控制荷载组合效应的重要参数,应尽可能取小值以有效抑制主梁端部的纵向位移,控制伸缩缝的位移量。当前镇宁岸及水城岸主梁端部均无纵向约束,不考虑限位阻尼器时,主梁端部相对于索塔横梁的纵向位移如表1所示。
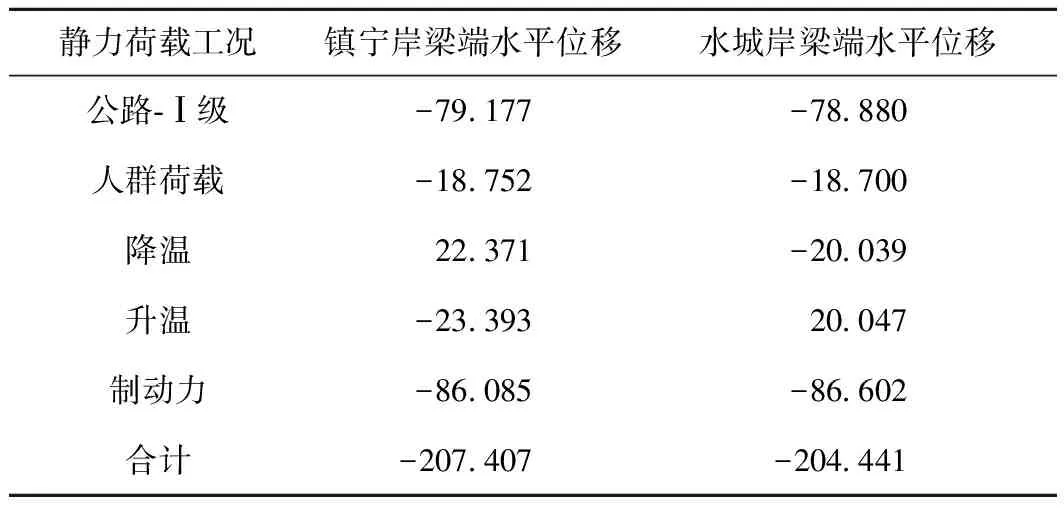
表1 各静力荷载工况下塔梁相对水平位移 mm
由表1可知,无纵向约束时两岸主梁端部位移在静力工况组合下最大相对位移均超过200 mm,远超过设计水平位移量80 mm。为此,拟定各限位阻尼器的额定行程(初始间隙)为30 mm,通过静力、地震反应确定限位阻尼器的各项性能指标。
3.2 限位阻尼器弹性刚度参数分析
在荷载作用下,当主梁端部与索塔横梁的相对位移达到额定行程(初始间隙)后,阻尼器进入弹性限位状态[6]。此时,阻尼器的弹性刚度开始约束主梁与桥塔横梁的相对运动,该状态下塔梁连接装置的作用相当于一个具有初始间隙的非线性弹簧。
在布置限位阻尼器后,阻尼器弹性刚度取值对静力反应的影响见图4,其中,塔顶纵向位移、主梁端部相对位移、塔底弯矩由公路-Ⅰ级、人群荷载、升温和制动力共同作用时经非线性分析计算得到。
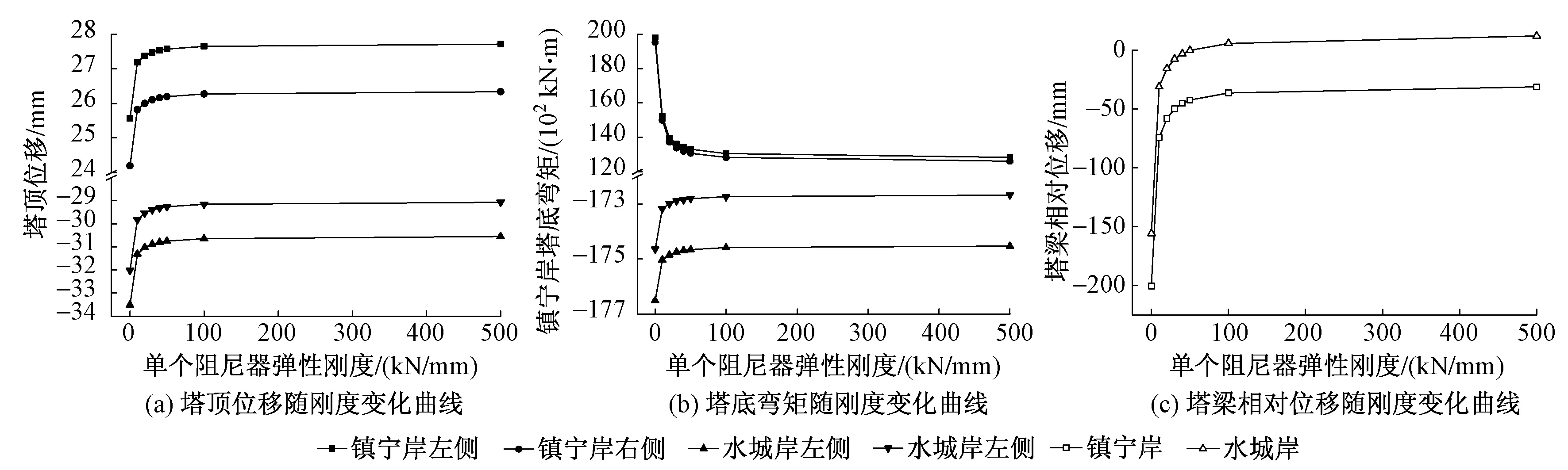
图4 阻尼器弹性刚度取值对静力反应的影响
由图4可知,限位阻尼器的弹性刚度为0~100 kN/mm 时,主梁端部与索塔相对位移变化非常剧烈,随后则趋于平坦。塔顶位移及塔底弯矩随弹性刚度变化趋势与塔梁相对位移变化趋势保持一致。随着限位阻尼器弹性刚度的增大,镇宁岸塔顶纵向位移变大,而水城岸塔顶纵向位移变小,总体变化幅值较小,不超过8%。水城岸塔底弯矩变化幅度较小,镇宁岸塔底弯矩减小的趋势较为显著,当弹性刚度达到100 kN/mm后,减幅达34%。主梁端部相对位移减小的趋势明显,当弹性刚度达到100 kN/mm后,两岸两端位移减幅达82%。
根据分析结果可知,阻尼器弹性刚度取30 kN/mm时,可以减小静力作用下塔梁相对位移以及塔底弯矩。
3.3 限位阻尼器阻尼系数分析
黏滞型阻尼装置是一种速度相关型阻尼装置,其阻尼力-位移滞回曲线近似矩形。动力特性稳定,且不改变结构固有特性,在额定行程内不增加结构刚度,只提供附加阻尼[7],其输出方程为
F=CVα
式中:F为阻尼力;C为阻尼系数;V为最大反应速度;α为速度指数。
阻尼系数取值对地震反应的影响见图5。
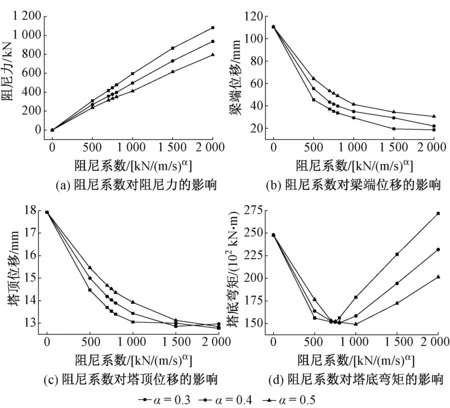
图5 阻尼系数取值对地震反应的影响
由图5可知:
1)当α一定时,随着C的增大,塔顶位移和塔梁相对位移总体减小。当C>1 500 [kN/(m/s)α]时,塔顶位移塔梁相对位移变化趋缓,塔顶位移减幅超过28%,塔梁相对位移位移减幅超过69%;
2)当α一定时,塔底弯矩随C的增大呈先减小后增加的趋势,C在750 [kN/(m/s)α]左右时,塔底弯矩达到最小值;主塔塔底弯矩最大值与最小值之比大于1.632;
3)当C一定时,α越小,塔梁相对位移越小,三者数值相差总体也越小。而塔顶位移在C达到2 000 [kN/(m/s)α]后趋于一致;
4)当C一定时,α越小,阻尼力越大,三者数值相差也越大;
5)当C<750 [kN/(m/s)α]时,α越大,主塔塔底弯矩越大;当C>750 [kN/(m/s)α]时,α越大;主塔塔底弯矩越小。
兼顾悬索桥塔底受力和梁端位移的原则,根据分析结果初步选取单个阻尼器的动力设计参数为阻尼系数C=1 000 [kN/(m/s)α],速度指数α=0.4。
4 塔梁纵向连接方式性能比较
阿志河大桥为阻尼限位约束体系、弹性约束体系和漂浮体系时的静动力效应的综合比较见表2。
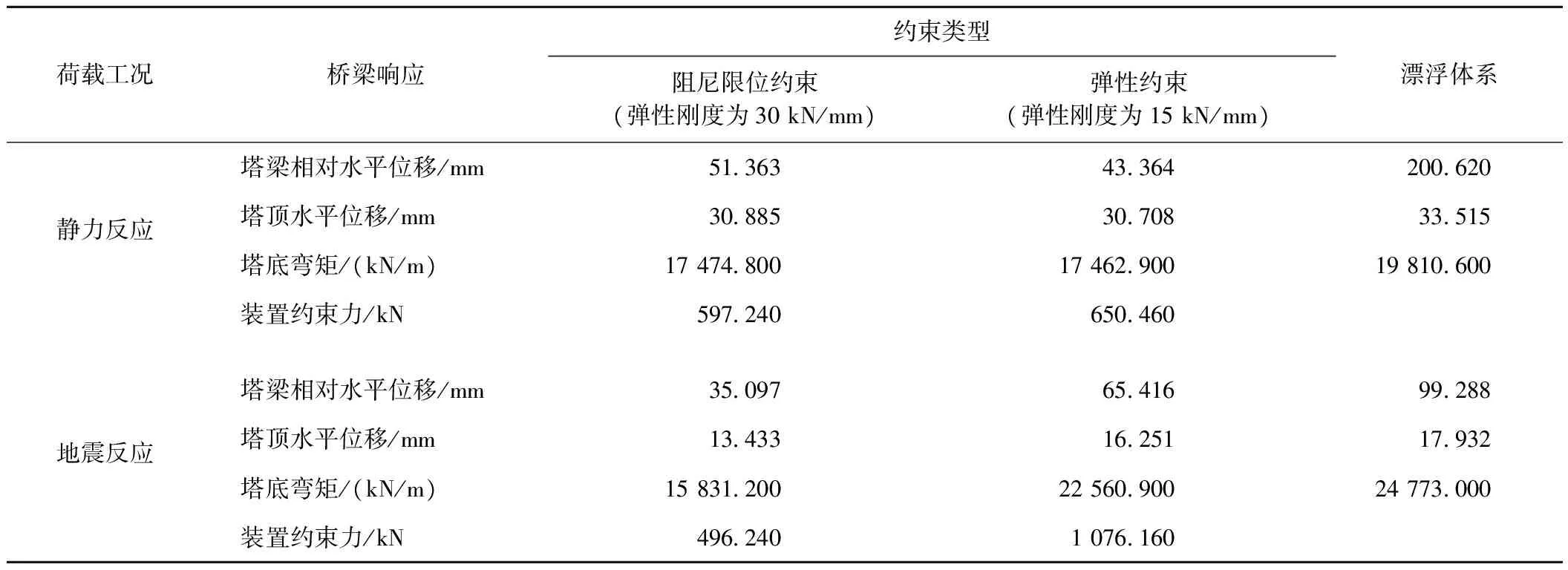
表2 2种约束体系与漂浮体系的综合比较
由表2可知:
1)就静力效应而言,阻尼限位约束体系和弹性约束体系对于桥梁各项响应值几乎一致,2种约束体系与漂浮体系相比,塔梁相对水平位移减小幅度超过74%,塔顶水平位移和塔底弯矩也有一定程度的减小。
2)就地震效应而言,阻尼限位约束体系与弹性约束体系、漂浮体系相比,塔梁相对水平位移减小幅度超过46%,塔底弯矩减小幅度超过30%。同时,阻尼限位约束体系装置约束力约为弹性约束体系的46%,减小了主塔在地震反应中的受力。
5 结论
1)对于阿志河大桥而言,漂浮体系不是一种理想的结构体系,其在静力和地震反应中均产生较大的塔梁相对水平位移及塔底弯矩。
2)阻尼限位约束体系和弹性约束体系均能有效地降低塔梁相对水平位移和塔底弯矩。
3)与弹性约束体系相比,阻尼限位约束体系在地震反应中桥梁各关注项目的响应值均较小,同时有效提高了桥梁刚度、改善了结构阻尼。虽然弹性约束造价低廉,经济性较好,阻尼限位约束制造和维护困难,但阻尼限位约束在静力反应中允许一定的自由位移,考虑到主塔受力,在新桥设计与梁端相对水平位移过大的旧桥加固项目中推荐使用阻尼限位约束体系。
[1]肖汝诚.桥梁结构体系[M].北京:人民交通出版社,2013.
[2]齐东春,汪洪星.空间缆索悬索桥主缆扭转的模型试验[J].铁道建筑,2016,56(2):14-17.
[3]交通部公路规划设计院.JTJ 021—1989公路桥涵设计通用规范[S].北京:人民交通出版社,1989.
[4]中华人民共和国交通运输部.JTG D60—2015公路桥涵设计通用规范[S].北京:人民交通出版社,2015.
[5]谢群华.约束体系对大跨度斜拉桥抗震性能的影响研究[J].现代交通技术,2016,13(3): 40-2.
[6]徐利平,张喜刚,裴岷山,等.苏通大桥主桥结构体系研究[C]//中国公路学会桥梁和结构工程分会2004年全国桥梁学术会议论文集.北京:人民交通出版社,2004:20-25.
[7]陈永祁,马良喆.桥梁用液体黏滞阻尼器的减振设计[C]//第十八届全国桥梁学术会议论文集.北京:人民交通出版社,2008:877-885.

