永定河大桥主桥钢箱梁高腹板稳定性研究
张 为
(北京市市政工程设计研究总院有限公司,北京 100082)
长安街西延永定河特大桥位于“神州第一街”长安街与北京“母亲河”永定河的交汇处。桥梁结构形式为高低拱形钢塔、横梁连接分离钢箱斜拉刚构组合体系桥。
桥梁中线与河道中线斜交角为57.40°。主桥全长639 m,双向八车道。桥梁标准宽度47 m,局部全宽54.90 m(高塔处)。桥梁面积 31 174 m2。索塔采用全钢结构,高塔位于桥面上部高度约为112 m,南北塔倾斜角分别约为61°和71°。主梁采用全焊接分离式变截面钢箱,中间用横梁联结,横梁间距3 m,车行道部分为正交异性钢桥面板。中跨主梁宽度从54.9 m至47.0 m再至53.7 m渐变,梁高从10.51 m至3.3 m渐变,边跨主梁宽度为47 m,梁高3 m。主纵梁中孔钢梁由跨中的单箱四室变化至塔根部的单箱五室,塔根部钢箱腹板板厚40 mm,跨中板厚16 mm。每个腹板在单侧设置纵肋和横肋,并均设于腹板变厚度一侧。横肋为T形肋,设置在相邻隔板中间,其腹板距离钢箱顶底板400 mm。纵肋采用板肋和T肋相结合的方式,梁根部最多7根,至跨中逐渐减少为3根[1]。
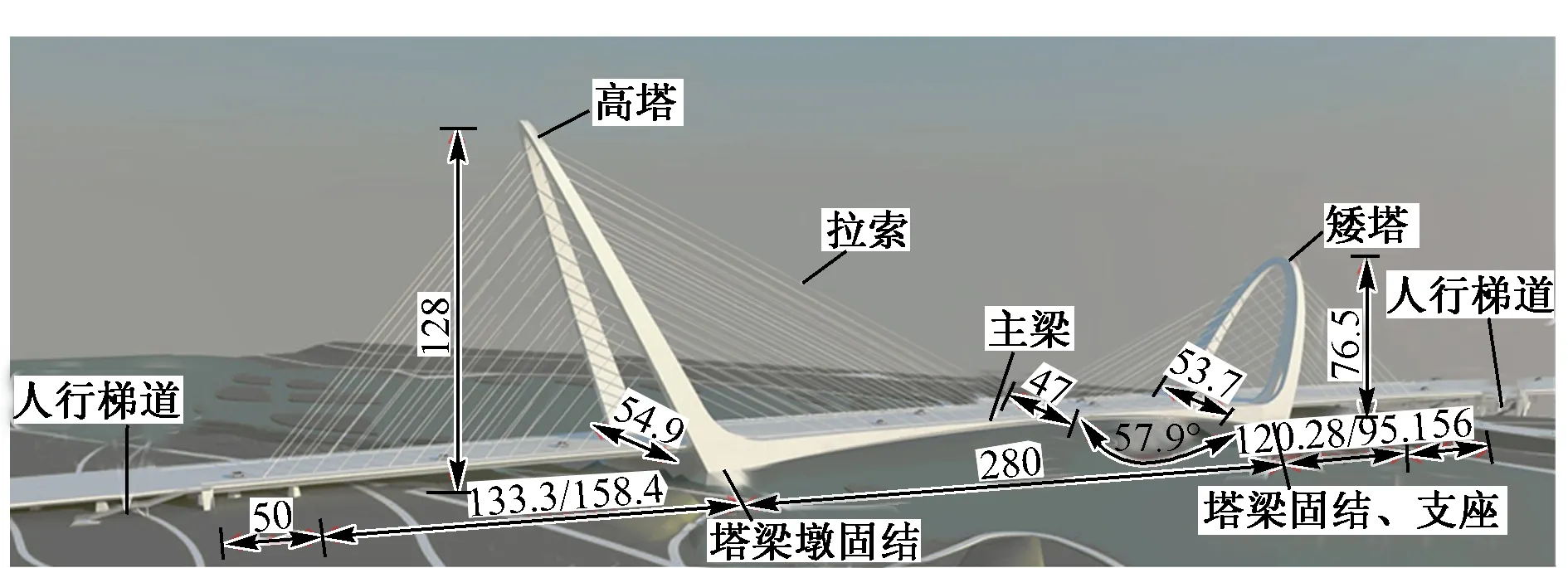
图1 永定河特大桥主桥三维模型(单位:m)
永定河大桥钢箱梁腹板最大高度为10.51 m,是国内已建和在建桥梁工程中钢箱高度最大的桥梁结构,超过了采用9 m梁高的崇启大桥,故其高腹板稳定性问题需深入研究。
1 钢箱梁腹板稳定性研究方法概述
钢箱梁腹板受力较为复杂,其不但承受剪力和扭矩产生的剪应力,同时还要承受弯矩产生的弯曲应力及轴力产生的压应力。这使得钢箱梁腹板的稳定性问题变得更为突出[2-3]。通过总体强度计算及根据相关规范要求确定腹板最小厚度后,提高腹板稳定临界应力的措施主要有增加板厚和设置加劲肋2种方式,其中设置加劲肋的效果显著。横向加劲肋主要用于防止腹板剪切失稳和集中力作用导致的应力集中问题。纵向加劲肋的主要作用是防止腹板在弯曲压应力作用下的压弯失稳。腹板厚度不应过小,需在加劲肋与腹板用料之间寻找一个平衡点。
诸多国内外钢结构设计规范对于钢箱梁腹板加劲肋设计给出了相关规定(见表1),包括GB 50017—2003《钢结构设计规范》[4]、JTG D64—2015《公路钢结构桥梁设计规范》[5]、TB 10002.2—2005《铁路桥梁钢结构设计规范》[6]、《道路桥示方书·同解说Ⅳ钢桥篇》(日本钢桥规范)[7]、BS 5400(英国规范)[8]。
设置加劲肋的目的在于使腹板划分为不同的区格,每个区格均要满足要求,才能确保不发生腹板局部屈曲。对于钢箱梁腹板,根据弯矩和剪力的分布可知,靠近梁端部的区格主要受剪力作用,而在跨中附近的区格则主要受弯曲正应力作用,其他区格则常受正应力和剪应力的联合作用。

表1 各规范对腹板横向和纵向加劲肋构造要求
注:b0,hs为加劲肋的伸出肢肢宽;h,h0为腹板的计算高度;tw,ts为加劲肋的肢厚;Ic为加劲肋对腹板中线的惯性矩;δ,t均为腹板板厚;a为横向加劲肋的间距;Iz,Iy分别为横向、纵向加劲肋截面惯性矩;I1为加劲肋截面惯性矩,单侧设置时对腹板连接线惯性矩,双侧设置时对腹板中心线惯性矩;A1为加劲肋截面面积;b为加劲板宽(腹板高);n为被加劲肋分隔的局部板件数目;It纵肋对腹板截面的惯性矩;γv,req为加劲肋临界刚度比,γv,req=30a/b;横肋对腹板截面的惯性矩γv,req=8a/b;b1为加劲肋间距;δy为腹板材料屈服强度。
关于腹板区格的稳定性验算,各国规范要求大同小异,在此不一一赘述。值得一提的是,GB 50017—2003和BS 5400均考虑了横向应力作用的影响,而日本钢桥规范和JTG D64—2015则没有考虑横向应力作用。针对永定河大桥的特殊结构体系所造成的主梁受力特点,需充分考虑横向应力作用,且JTG D64—2015中腹板稳定性验算的内容同样参考了日本规范,故本文后续主要参照GB 50017—2003和日本钢桥规范。
2 钢箱梁高腹板加劲肋刚度验算
2.1 纵肋刚度验算
永定河特大桥钢腹板水平方向铺设的纵肋采用单侧扁钢。腹板纵肋的刚度验算主要参照我国规范GB 50017—2003中4.3.6(4)条及日本钢桥规范中10.4.7(1)条。对腹板纵肋进行刚度验算,主梁纵肋设计值与需求值的对比见图2。
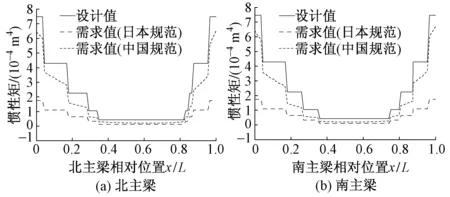
图2 主梁纵肋设计值与需求值的对比
2.2 横肋刚度验算
永定河特大桥腹板竖向设置的横肋考虑了2种方案:方案1是双侧T型钢加劲肋设计,方案2是单侧T型钢加劲肋设计。验算主要采用GB 50017—2003 4.3.6(3)条及日本的钢桥规范10.4.4条。方案1和方案2分别对腹板垂直方向铺设的横肋进行刚度验算,北主梁横肋设计值与需求值的对比见图3。
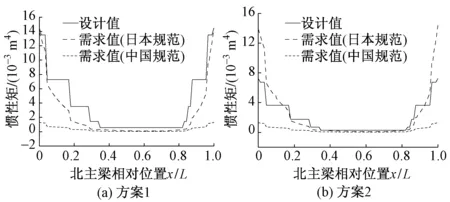
图3 北主梁横肋设计值与需求值的对比
由图3可知,当横肋采用单侧T肋时,刚度验算满足我国规范设计要求,但采用日本规范对刚度进行验算时,临近高塔和矮塔部分的主梁梁段略有不足。
2.3 高腹板最小厚度及纵肋位置合理性验算
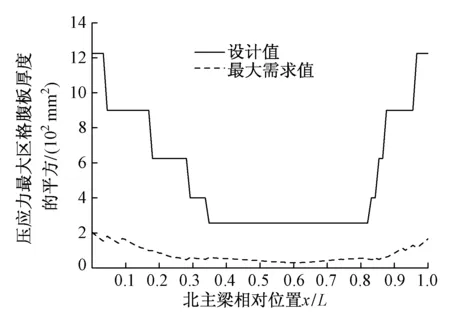
图4 北主梁压应力最大区格腹板厚度设计值与 需求值对比
腹板厚度设计参照日本钢桥规范10.4.2条,对腹板的最小板厚进行验算。按照公式计算所需腹板厚度的平方并与当前设计腹板厚度的平方对比(遍历所有内力组合计算腹板厚度需求值,筛选出各截面位置处腹板厚度的最大需求值)。北主梁压应力最大区格腹板厚度设计值与需求值对比见图4。可知,在压应力最大区格内,最大需求的腹板厚度小于设计值,故满足设计厚度以及纵肋位置的合理性验算要求。
3 钢箱梁高腹板稳定性区格验算
腹板板块受纵向弯曲应力、横向应力、剪应力的屈曲交叉影响,参照GB 50017—2003 4.3.4条对腹板各区格进行局部稳定性验算。针对受压翼缘与纵肋之间区格、受压纵肋之间区格的稳定性验算,GB 50017—2003 只给出了受压翼缘与纵肋之间区格的稳定性验算方法,对受压纵肋之间的区格稳定性验算则没有给出明确规定。而文献[9]提出:“所有内侧的腹板板块(即不与翼缘毗连者)都可按在面内有约束处理”,即受压纵肋之间区格也可按受压翼缘与纵肋之间区格的稳定性验算方法进行验算,将受压应力较大的纵肋视作受压翼缘即可。
由于纵肋均布,在同一截面上的各区格高度相同,故在同一截面处的正应力σ、剪应力τ、局部压应力σc的临界值相同。剪应力根据规范要求取腹板平均剪应力,同一截面处各个区格的剪应力相同,各截面处只需考虑正应力最大的区格即可,σc经计算取11.57 MPa。图5给出了北主梁受压区格最不利稳定性验算结果,可见在各组合工况下,其稳定性系数均<0.7,满足规范要求。
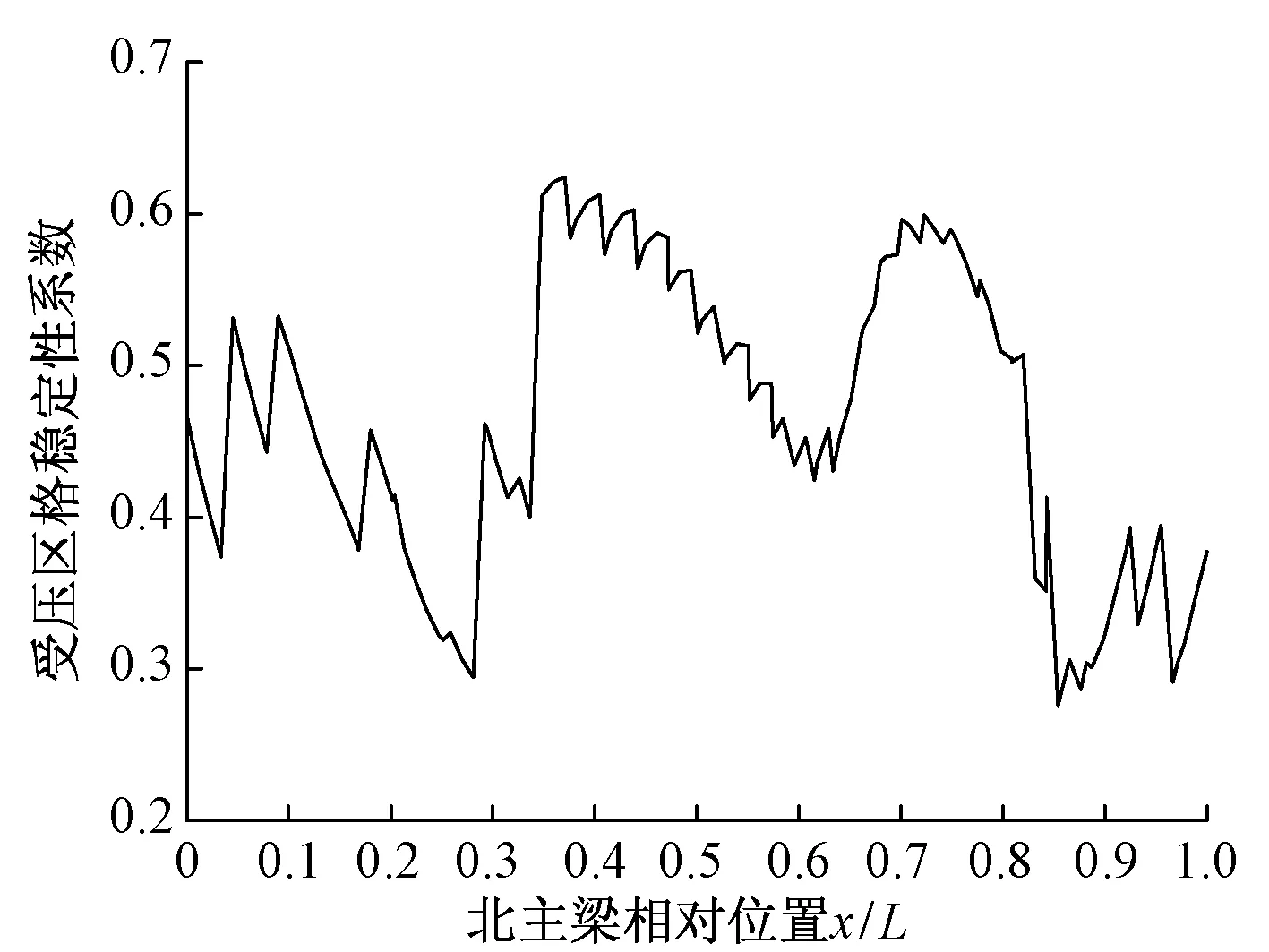
图5 北主梁受压区格最不利稳定性验算结果
4 钢箱梁高腹板稳定性有限元分析
4.1 高腹板局部稳定性模拟的主要问题
钢箱梁腹板的局部稳定性模拟需要考虑的主要问题为几何非线性、材料非线性、结构的初始几何缺陷和残余应力[9]。第2类稳定问题的实质是极限承载能力的问题,失稳方式为极值点失稳,失稳荷载为极限荷载,其整体和局部稳定相互影响的问题是一个整体-局部非线性相关稳定性承载力问题。利用有限元软件ABAQUS建立桥梁结构有限元模型,单元采用S4壳单元。
4.1.1 腹板的初始缺陷
采用构件一阶屈曲模态作为初始缺陷的形态,考虑TB 10212—98《铁路钢桥制造规范》对腹板局部变形精度的要求,结合欧洲规范[10]的建议,幅值取允许制造偏差的80%作为初始缺陷引入。引入方法为先计算结构一阶屈曲模态,并输出位移结果的二进制文件,进而通过关键字*IMPERFECTION 在后续极限承载力分析前引入模型。
4.1.2残余应力及其分布
根据文献[11]可知,对于本桥,沿焊缝方向考虑2类残余应力:①垂直于焊缝方向的残余应力,焊缝影响范围300 mm内为拉应力,两侧为压应力;②平行于焊缝方向的残余应力,腹板中部为拉应力,两端为压应力。假定焊缝处拉应力区域拉力的大小与压应力区域压力的大小数值相等,拉应力大小等于钢材的屈服强度。由于残余应力在构件内部是自相平衡的内应力,不会对构件总截面产生轴向的拉力或压力,故残余压应力σR的计算公式为
式中:C为与焊接方法有关的试验参数,取值范围7.5~12.5 kN/mm2;AW为焊缝面积,取400 mm2;Ag为区格总面积;σy为正应力。
计算得σR=80.7 MPa。采用预定义应力场考虑残余应力影响。
4.2 有限元计算结果
选取塔根部截面的F2腹板中的一个节段作为研究模型。腹板高10.5 m,节段宽3 m,根据文献[10]对有效宽度的规定,顶板有效宽度 1 633 mm,底板有效宽度 1 542 mm。
4.2.1弹性屈曲分析
弹性屈曲分析时,对腹板加载端节点采用MPC-Beam技术,模拟横隔板对加载边的限位作用,保证整个加载边始终保持直线。对控制点施加节点集中力,集中力取该截面上翼缘折算应力的1/4,约为25 MPa时的等效力,其值为8.75 MN。计算得一阶屈曲模态特征值为18.090,对应屈曲轴力为158.29 MN。垂直肋板的加劲作用使得腹板仅在受力侧产生屈曲;水平肋板的加劲作用,使得各个区段内产生相互交替出现一个半波。
4.2.2极限承载力分析
高腹板极限承载力分析荷载系数与加载点位移关系曲线见图6。极限荷载系数为13.144,极限承载力为115.01 MN。极限荷载下高腹板的屈曲变形如图7所示,表现为肋间腹板的翘曲变形,在加载方向丧失承载力。
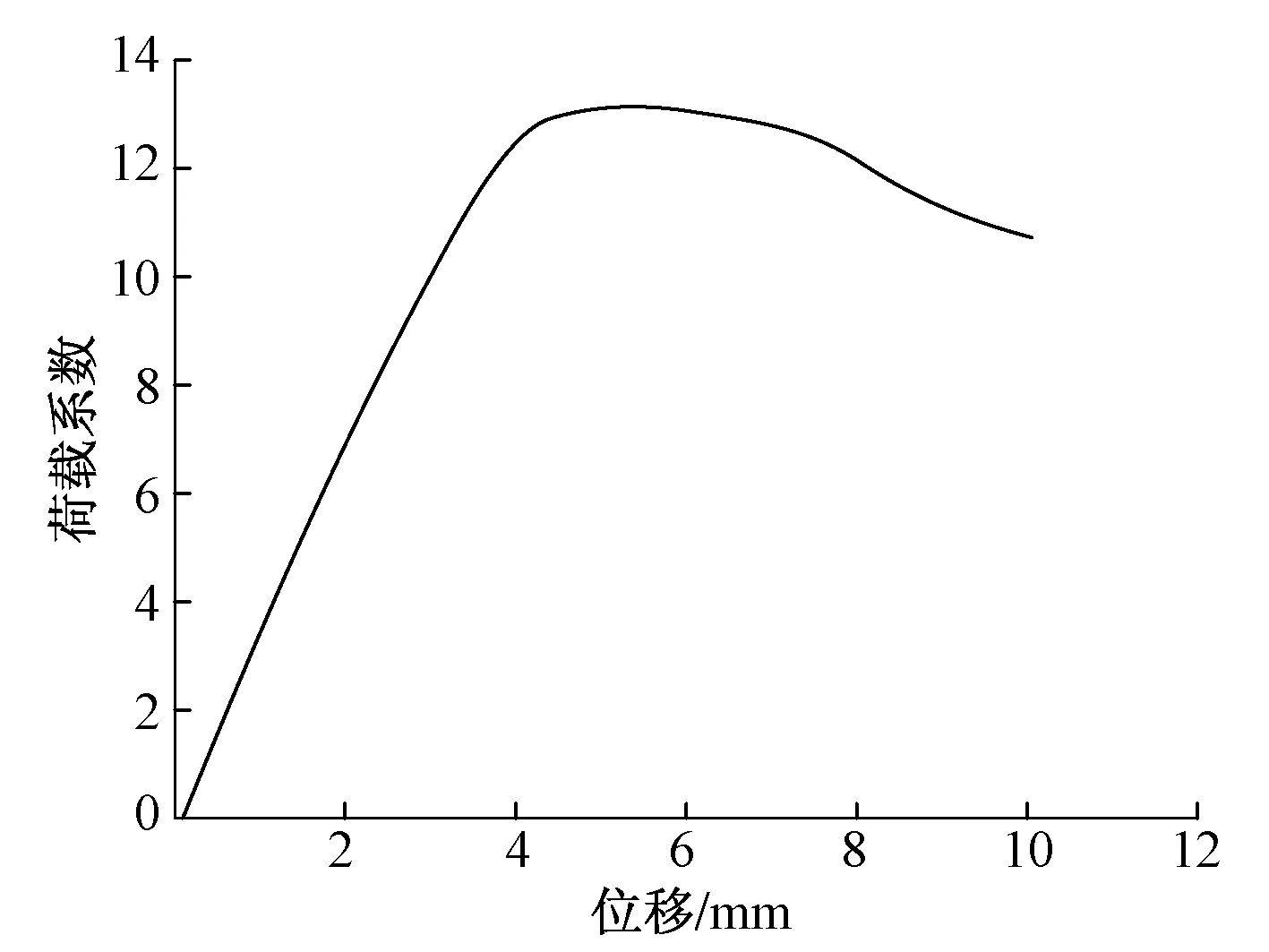
图6 高腹板极限承载力分析荷载系数与位移的关系曲线
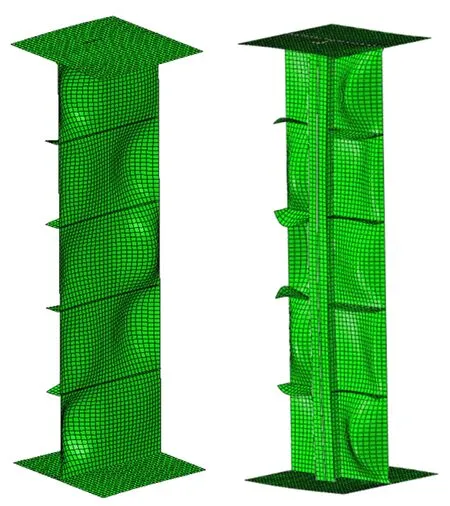
图7 极限荷载下高腹板的屈曲变形示意
4.2.3双侧横肋方案
相比于单侧横肋方案,双侧横肋布置的计算结果主要不同之处为:①一阶屈曲模态特征值为18.659,相对单侧布置提高约3.15%;②双侧布置方案极限荷载系数为13.261,相对单侧布置提高约0.89%,提高幅度较小。
5 结论
本文结合国内外相关规范对永定河特大桥钢箱梁高腹板的稳定性进行验算,并与有限元计算结果进行对比分析。主要结论如下:
1)根据永定河特大桥及各规范的特点可知,钢箱梁高腹板的强度验算参照我国《钢结构设计规范》和《公路钢桥设计规范》;腹板纵横肋的刚度验算参照我国《钢结构设计规范》及日本的《道路桥示方书·同解说》;高腹板最小厚度及纵肋位置合理性验算参照日本的《道路桥示方书·同解说》;高腹板区格稳定性验算参照我国《钢结构设计规范》。验算结果均满足要求。
2)钢箱梁高腹板横肋双侧布置T肋可同时满足我国及日本规范要求,纵肋、横肋均有较大刚度,使用辅助钢材较多,经济性较差;单侧布置T肋,可满足我国规范要求,但无法满足日本规范中对于主梁两端靠近桥塔处的刚度需求。竖向稳定性在实际成桥状态下并无较高要求,而顺桥向受压稳定性两者相差不大,综合经济性因素及遵循少焊原则,推荐采用单侧布置T肋方案。
3)腹板屈曲稳定性分析需重点考虑第2类稳定的非线性因素影响,包括初始几何缺陷、材料非线性、残余应力、大变形等。永定河大桥高腹板计算所得非线性屈曲系数大于全桥非线性屈曲系数,验证了高腹板局部失稳不会先于整体失稳。
[1]曾志斌,郭辉.长安街西延( 三石路—古城大街) 道路工程——永定河特大桥主桥钢结构稳定性研究[R].北京:中国铁道科学研究院,2015.
[2]赵秋,王欣南.桥梁钢箱梁腹板设计计算方法探讨[J].钢结构,2013,28(4):32-36.
[3]武芳文,张庆开,李长学.曲线桥单箱多室钢箱梁制作技术与质量控制[J].铁道建筑,2016,56(3):21-24.
[4]中华人民共和国建设部,中华人民共和国国家质量监督检验检疫总局.GB 50017—2003钢结构设计规范[S].北京:中国计划出版社,2003.
[5]中华人民共和国交通运输部.JTG D64—2015公路钢结构桥梁设计规范 [S].北京:人民交通出版社,2015.
[6]中华人民共和国铁道部.TB 10002.2—2005铁路桥梁钢结构设计规范[S].北京:中国铁道出版社,2005.
[7]日本土木学会.道路桥示方书·同解说[S].东京:日本土木学会,2012.
[8]BS 5400-3:2000Steel,Concrete and Composite Bridges-Part 3:Code of Practice for Design of Steel Bridges[S].Brussels:CEN,2000.
[9]陈骥.钢结构稳定理论与设计[M].北京:科学出版社,2006.
[10]BS EN 1993—2:2006Eurocode 3-Design of Steel Structures-Part 2:Steel Bridges [S].Brusseds:CEN,2006.
[11]SUKHEN C.The Design of Modern Steel Bridges[M].Blackwell Science Ltd,a Blackwell Publising Company,2003.

