用简单的方法验证点电荷概念的相对性

孔　文

（安徽大学江淮学院，安徽　合肥　230031）

点电荷本质上就是带电体，是一个没有大小形状的集合点.而电荷又全部集中在这个几何点上.事实上，任何带电体都有大小和形状，真正地点电荷是不存在的，它像力学中的“质点”概念一样，纯属一个理想化模型[1].不过，当我们在研究带电体激发的电场分布及相互作用时，如果带电体本身的几何限度比起它们之间的距离小得很多，那么，带电体的形状、大小的电荷分布对带电体之间的相互作用的影响就可以忽略不计.在此情况下，我们仍可以把带电体抽象成点电荷模型.也只有这样，“电荷之间的距离”这一概念才有完全的确定的意义[2].故从此角度看，点电荷又是一个相对性概念.为了能对点电荷的相对性认识的更加充分，更加深刻.我们从电偶极子、线带电体、面带电体、球带电体的特殊场点来计算场强分布特点.

1　点电荷电场强度

设在真空中有一个静止点电荷q，则距为r的P点的电场强度，可由库伦定律求得.在P点放一试探电荷q0，可知，作用在q0上的电场力是

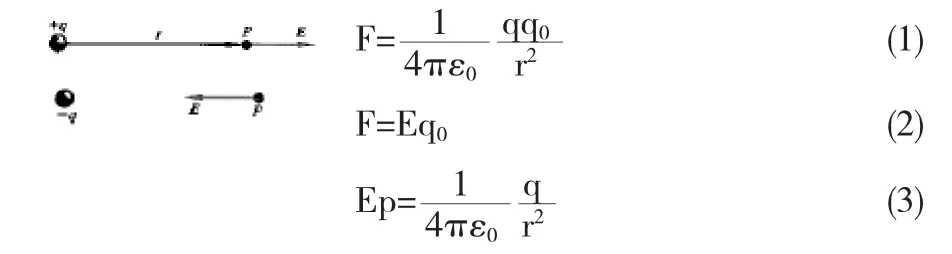
由（3）可知，点电荷q在真空中任意一点激发的电场强度大小，与点电荷电量成正比，与点电荷到该场点的距离的平方成反比.

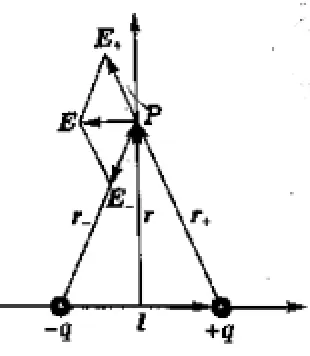
2　同性等量点电荷在中垂线上电场强度

设在真空中有两个等量同性点电荷，电量均为q；q1q2距离21，O为中点，到O的距离为r.

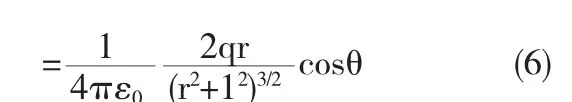
讨论，当 r≫1，即 limr→∞(r2+12)=r2；limθ→0cosθ=1 可得，

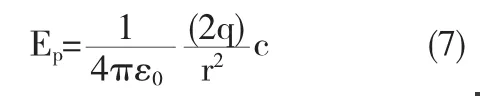
由（7）可见，当P点沿中垂线离开O点的距离比点电荷系本身的大小大的多时，P点的电场强度与一个电量为2q的在O点的点电荷电场强度相等，即验证了点电荷概念的相对性.完全可以把该模型当做点电荷模型来处理相关问题.

3　有限长线带电体电场强度

3.1　带电直导线在延长线上电场强度

设真空中有带电直导线长1，带电量Q（均匀带电），在导线的延长线上电场强度满足何种分布规律?若满足一定的条件，线点电荷场强分布模型是否又可转化为点电荷模型.

P点距导线一段端的距离是d，另一端为O点向右建立x轴坐标系，在导线任意位置取一个点电荷dq，dq到O点的距离是x，则dq在P点的场强

根据电场叠加原理

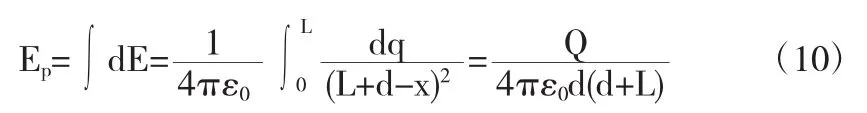
讨论，若满足 d≫L，limd→∞d(d+L)2=(d+L)2

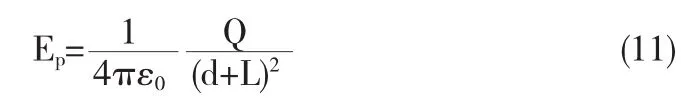
由(11)可见，当场点P距导线的一端的距离远大于导线自身长度时，P点的场强与把所有电量Q集中在O点的一个点电荷在同样场点的场强相等.验证了点电荷概念的相对性.完全可以把该模型当做点电荷模型来处理相关问题.

3.2　带电直导线在中垂线上电场强度

设真空中有带电直导线长2L，带电量Q（均匀带电），O是导线中点，P到O的距离为r.导线的中垂线上电场强度满足何种分布规律?若满足一定的条件，该模型模型是否又可转化为点电荷模型.

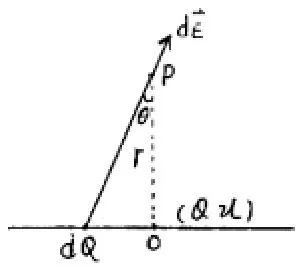
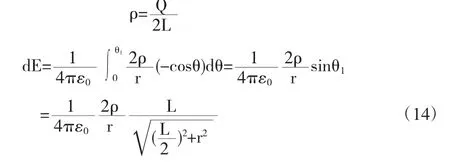
由(15)可见，当导线中垂线上场点P距导线的距离远大于导线自身长度时，P点的场强与把所有电量Q集中在O点的一个点电荷在同样场点的场强相等.验证了点电荷概念的相对性.完全可以把该模型当做点电荷模型来处理相关问题.

3.3　带电圆周导线在轴线上电场强度

设Oyz平面内有一半径为R的圆环，均匀带有电量Q，则轴线上任意一点P的电场强度满足何种分布规律？若满足一定的条件该模型模型是否又可转化为点电荷模型.

讨论，若 x≫R；limx→∞(x2+r2)3/2=x3

由(19)可见，当带电圆周导线轴线上场点圆心的距离远大于导线自身长度时，P点的场强与把所有电量Q集中在O点的一个点电荷在同样场点的场强相等.验证了点电荷概念的相对性.完全可以把该模型当做点电荷模型来处理相关问题.

4　有限大带面带电体电场强度

设Oyz平面内有一半径为R的圆盘，均匀带有电量Q，则轴线上任意一点P的电场强度满足何种分布规律？若满足一定的条件该模型模型是否又可转化为点电荷模型.

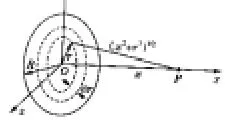
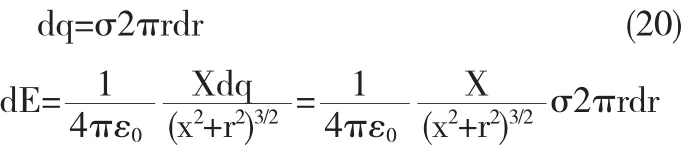
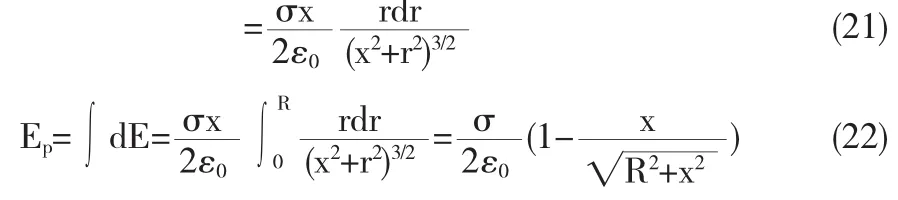
讨论，若x≫R，利用二项式定理展开

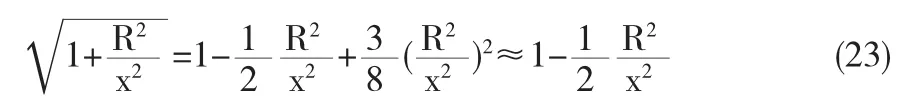
将（23）代入（4-3）Ep=

由(24)可见，当带电圆盘轴线上场点距圆心的距离远大于自身大小，P点的场强与把所有电量Q集中在O点的一个点电荷在同样场点的场强相等.验证了点电荷概念的相对性.完全可以把该模型当做点电荷模型来处理相关问题[3].

5　带电球体外场电场强度

设带电球体均匀带电电量Q，球体半径为R，球体外任意一点P的电场强度满足何种分布规律？

由(26)可见，球体外P点的场强与把所有电量Q集中在圆心点的一个点电荷在同样场点的场强相等.验证了点电荷概念的相对性.完全可以把该模型当做点电荷模型来处理相关问题.

6　结束语

通过以上几个特殊的模型我们不难发现，当场距远大于带电体自身的尺寸时，不管带电体所带电量有多大，在特殊场点上的电场分布无一例外的都是满足点电荷电场强度分布.这里值得一提的是，虽然本文所选的模型具有一定的特殊性（所带电荷对称分布），所讨论的场点也是特殊位置，但是不可否认的是，原则上总可将带电梯看成是由无数个点电荷元所组成的连续点电荷系.[4]然后在利用适用点电荷相互作用规律的库伦定律，通过求和或者积分求出电场分布，其结果也可以证明电场分布与源电荷的电量成正比与场距的平方成反比的结论，这个结论另做讨论.

参考文献：

〔1〕孔祥鲲.基于MATLAB构建点电荷系的电势与电场强度分布图[J].实验技术与管理，2007，24（10）.

〔2〕刘耀康.用计算机绘制点电荷对的电场线[J].大学物理，2005，24（8）.

〔3〕程守洙.普通物理学[M].北京：高等教育出版社，2006.

〔4〕韩家华.大学物理学[M].合肥：安徽大学出版社，2009.