机床导轨形位误差不确定性对加工误差的影响*

马雅丽，李阳阳

(大连理工大学 机械工程学院，辽宁 大连　116024)

0　引言

中国制造2025将高档数控机床列为十大重点领域，高精机床亦是机床行业发展的重点。导轨是机床重要的零部件，其误差直接影响机床的加工精度，因此在机床设计阶段分析导轨的误差是很有意义的。

机床的加工误差体现在刀具切削点实际位置与理想位置的偏差，是由各类误差传递与耦合而成，其中零部件的几何误差产生的误差占了很大部分。程强[1]等基于多体系统理论，提出了关键性几何误差源识别的方法，可以有效地识别对机床空间误差影响较大的零部件几何误差因素。基于多体系统和齐次坐标变换理论，粟时平[2]和杨建国[3]建立了五轴机床的精度模型。Majda[4]采用有限元方法将导轨形位误差等效为弹簧单元变形量，分析了导轨形位误差对运动误差的影响。考虑形位误差、热误差、弹性变形，Rahman[5]基于齐次坐标变换建立了机床空间误差模型。

然而，零件加工之前误差是未知的，具有不确定性，导致整机误差的不确定性。因此，考虑形位误差的不确定性进行机床加工误差的分析更符合工程实际。文献[6]考虑支承件材料密度、弹性模量和载荷的不确定性，提出了支承件多目标优化设计方法。当系统参数分布函数未知或者系统性能函数不可导时，常用的方法是采样统计法。采用蒙特卡洛模拟方法，崔鑫磊[7]等研究了支杆长度误差和轴承游隙对6-UPS并联机构动平台位姿误差的影响。余治民[8]等采用蒙特卡洛模拟与响应面法相结合的方法，提出了几何公差建模方法。

上述研究成果中的误差建模，多基于参量的确定性分析，缺少从参量不确定性的角度出发建立误差分析模型。因此，本文采用不确定性分析方法建立导轨误差与机床加工误差耦合分析模型。以区间参数和小位移旋量描述形位误差的不确定性，并基于蒙特卡洛方法模拟形位误差的实际变动分布范围。在进一步建立的导轨运动部件的运动误差模型基础上，最终建立了导轨误差与机床加工误差的分析模型。通过实例分析了导轨几何误差对机床加工误差的影响规律，为机床部件的精度分配提供支撑。

1　导轨形位误差不确定性分析

形位误差是指单一实际要素对其理想要素的变动量，包括形状误差和位置误差。导轨的形位误差直接影响运动零部件的运动误差，进而通过误差传递导致机床的加工误差。本节旨在建立导轨形位误差的不确定分析模型。

1.1　导轨形位误差矢量

形位误差可概括为点、线、面等基本几何要素相对理想要素的变动量。在三维空间中，误差变动量可描述为沿3个坐标轴的平动和绕3个坐标轴的转动，分别用d=(u,v,w)和θ=(α,β,δ)表示平动和转动的微小变动矢量，两组矢量的合成矢量D=(d,θ)= (u,v,w,α,β,δ)称为小位移旋量，简称旋量。u,v,w,α,β,δ为旋量的旋量参数。

不同类型误差的旋量特征不同。若几何要素沿某一个自由度方向运动时，其运动轨迹不产生新的误差扫掠实体，此时该方向的旋量参数为零。

1.2　导轨形位误差矢量变动区间

导轨形位误差在形位公差形成的公差带内变动。根据设计要求，导轨的形位误差主要包括安装主基准面的平面度误差、侧基准面的垂直度和平行度误差。其中主基准面A平面度公差为TA，宽度和长度分别为a和d；侧基准面B垂直度公差为TB，高度和长度分别为c和d；C平行度公差为TC，如图1所示。

图1　导轨安装基面尺寸及公差

以平面度误差为例，DT=(0,vT,0,αT,0,δT)为平面度误差的旋量，则其旋量参数变动区间为：

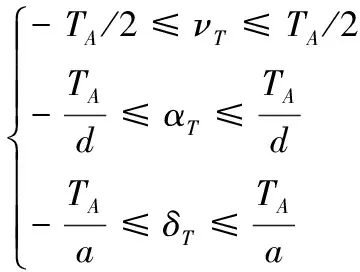
(1)

安装主基面内任意一点y方向坐标可以表达为：

(2)

其中，△yT表示A面内任意两点之间y方向的距离。对于限制在TA带内的矩形平面来说，极值情况发生在矩形平面的顶点处，因此，平面度误差旋量参数约束为：

-TA/2≤xδT+zαT≤TA/2

(3)

-TA/2≤νT+xδT+zαT≤TA/2

(4)

其中,x、z取值为A面的4个极限点位置，在图1中是安装主基面的4个顶点位置坐标。

1.3　基于蒙特卡洛模拟导轨形位误差的不确定性

导轨形位误差具有不确定性，其分布函数是未知的，常常用统计参数进行描述。因此，本文提出了基于采样统计法来模拟导轨不确定的形位误差。蒙特卡洛方法是一种通过对随机变量的统计实验和随机模拟来求解问题近似解的方法[9]。运用蒙特卡洛方法，对导轨形位误差旋量参数进行抽样实验，保留满足约束条件的随机数，去除不满足约束条件的随机数。以平面度误差旋量参数为例，具体步骤如下：

(1)确定平面度误差旋量参数的分布模型。形位误差由许多相互独立的随机因素互相影响，呈现无规则变化，因此可以假定其统计特性符合正态分布的变化规律，概率密度函数为：

(5)

其中，μ为算术平均值，σ为均方差。

(2)确定平面度误差旋量参数的均值与方差。可知概率密度函数中x的值出现在μ±3σ区间内的概率为99.73%，通常认为正态分布的分布范围是±3σ。根据旋量参数变动区间公式(1)，旋量参数vT，αT,δT的均值与方差分别为(0,TA/6)，(0,TA/3d)，(0,TA/3a)。

图2　平面度误差的抽样流程

(3)根据抽样要求对平面度误差旋量参数进行抽样，旋量参数抽取规则共有6种变动顺序。按照6种顺序分别进行抽样，可以得到总量为6×M3的满足约束范围的平面度误差旋量参数样本。以变动顺序(αT→δT→vT)为例，总的抽样流程如图2所示，采样样本总数为M3。

同理，也可以获取导轨垂直度误差旋量DZ=(μZ,0,0,0,βZ,δZ)和平行度误差旋量DY=(μY,0,0,0,βY,δY)样本。导轨的综合位姿偏差是由主基准面和侧基准面共同决定的，根据安装导轨的主从关系，最终左侧导轨和右侧导轨的位姿偏差旋量为(μZ,vT,0,αT,βZ,δT)和(μY,vT,0,αT,βY,δT)。

2　运动零部件不确定性运动误差建模

导轨的形位误差与运动误差会改变与滚动体的接触状态，进而影响滚动体的弹性变形量。本节将运动零部件的位姿误差与导轨形位误差等效为滚动体的弹性变形，结合赫兹接触理论建立运动零部件的静力平衡方程以及运动零部件的运动误差求解模型。

2.1　运动误差描述

滚动导轨副联接的零部件的结构如图3所示，其中导轨是固定零部件，滑块以及滑块上固定在一起的部件为运动零部件。

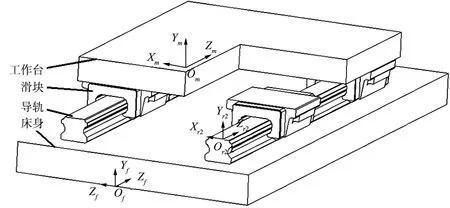
图3　滚动导轨副结构示意图

运动零部件的运动误差可以用滑块的位姿误差表示，其相对于理想位置有5个自由度误差(忽略沿着导轨运动方向的定位误差)，即X方向的水平位移误差δx、Y方向的竖直位移误差δx、绕X轴的角度误差εx、绕Y轴的角度误差εy和绕Z轴的角度误差εz。忽略角度误差的二阶小量，则滑块的位姿误差变换矩阵ΔTs可以描述为：

(6)

以双列四滚道导轨为例，假如第i个滑块第j列滚道第k个滚动体所在对应位置滑块滚道的曲率中心坐标是(xijk,yijk,zijk)T，则其位姿误差在水平和竖直方向的偏差量分别为δijkx和δijky可以表达为：

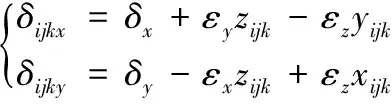
(7)

2.2　运动零部件运动误差等效模型

导轨形位误差和滑块位姿误差反映为滑块和导轨滚道曲率中心的偏移量，将形位误差和滑块位姿误差等效为滚动体的弹性变形，根据赫兹公式建立滑块的静力平衡方程。理想状态下，滚动体弹性变形之前的滑块与滚动导轨的几何关系如图4所示。

图中，Og和Oh分别是导轨和滑块滚道曲率中心。则导轨滚道的曲率中心与滑块滚道的曲率中心的距离L为：

L=|Og-Oh|=(2f-1)Da

(8)

此距离在X和Y方向上的分量分别为Lx0=(2f-1)Da*cosγ，Ly0=(2f-1)Da*sinγ。式中Da是滚动体公称直径，f是滑块和导轨滚道半径与滚动体直径的调整系数。

实际上，导轨滚道曲率中心有水平和竖直方向的偏移量Δijkx和Δijky；滑块滚道曲率中心有水平和竖直方向的偏移量δijkx和δijky,变形之后滚动导轨的几何关系如图5所示。

图4　滚动导轨几何关系

图5　变形后滚动导轨几何关系

因此，变形后滚动体的变化量为：

(9)

一般情况下，滚动导轨通过加大滚动体直接预紧，因此，若滚动体直径增量λ，其实际变形量为：

(10)

2.3　运动零部件的静力平衡方程

基于赫兹接触理论的弹性回复力与其弹性变形之间的关系，建立滑块在外载荷、重力以及所有滚动体回复力下的力和力矩平衡方程。根据赫兹接触公式，滚动导轨中单一滚动体弹性变形Δ与弹性回复力大小P之间的关系为：

P=(2η)-3/2Δ3/2

(11)

式中，η为与滚动体直径和滚道曲率有关的接触系数[10]。由公式(10)和(11)可以得到滚动直线导轨的接触力Pijk，在X和Y方向上的接触分力Pijkx和Pijky为：

Pijkx=Pijkcosβijk,Pijky=Pijksinβijk

(12)

其中，βijk是变形之后的接触角，βijk=artan|Lijky/Lijkx|。对于滑块而言，各个滚动体到滑块坐标原点的矢径可以记为rijk(rijk=(Xijk,Yijk,Zijk))。滑块在自身重力、外载荷、所有滚动体的弹性支反力下处于平衡状态，则滑块的弹性支反力及其合力矩与所受外力和外力矩的平衡方程为：

(13)

(14)

(15)

(16)

(17)

基于得到的滚动导轨形位误差旋量参数样本，联合方程(8)～方程(17)，可以得到运动零部件的运动误差。

3　机床加工误差不确定性模型

3.1　零部件之间的运动误差变换矩阵

根据多体系统理论，零部件Bj和零部件Bi相邻运动体之间有三个平动和三个转动的位置变化关系。在理想运动时，当零部件Bj是由零部件Bi先后沿着三轴平动的位移分别是uij,vij,wij和绕着三轴转动角度是αij,βij,δij，则根据齐次坐标变换理论，零部件Bi上坐标系Oi-XiYiZi到零部件Bj上坐标系Oj-XjYjZj变换矩阵为：

(18)

其中，c=cos,s=sin。在实际运动中，零部件Bj和零部件Bi存在着运动误差，包括三轴平动误差δx，δy，δz和三轴转动误差εx，εy,εz。根据公式(6)可知，零部件Bj和Bi之间的运动误差矩阵为：

(19)

3.2　机床加工误差不确定性建模

(20)

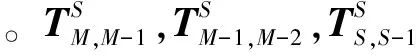
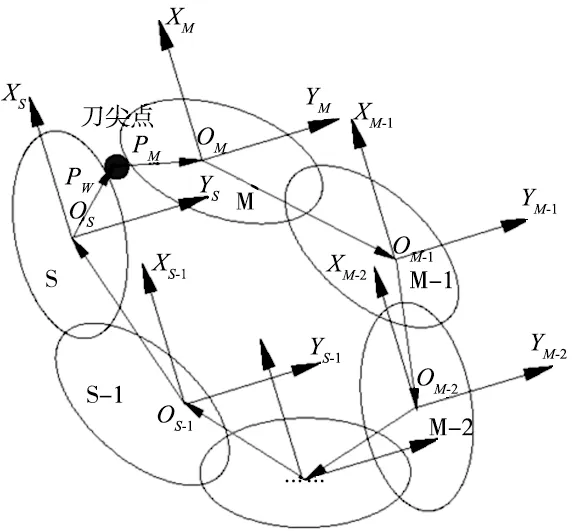
图6　机床零部件坐标系变换关系

(21)

E=Pw-Pw′

(22)

4　实例求解与分析

4.1　加工中心结构

以某车铣复合加工中心为例，计算机床不确定的加工误差，其结构如图7所示。为了研究各导轨形位误差对机床加工误差的影响，假定不同零部件同一类型的形位公差值相同。

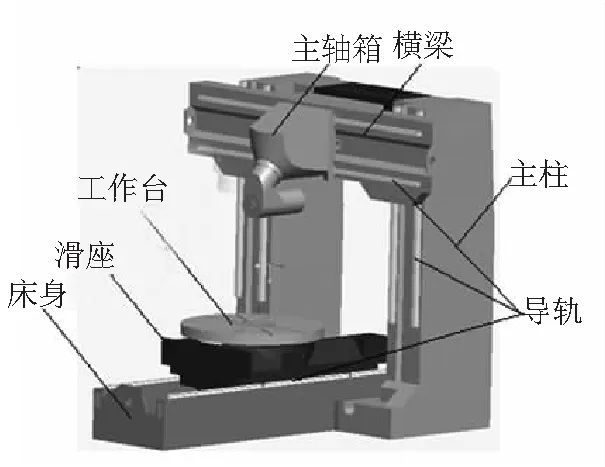
图7　复合加工中心三维模型

4.2　导轨平面度公差的影响

在导轨TB和TC为定值0.01mm时，根据建立的模型，探究机床加工误差与导轨TA的变化关系，结果如图8所示。可以看出，加工误差的分布宽度与平面度公差呈线性变化，但是平均值总体变化不大。从数值上分析，随着导轨TA从0.01mm增大到0.05mm时，机床三向加工误差在平均值附近的出现的概率减小，分散范围逐渐增加。其中，X向加工误差达到0.07mm；Y向加工误差达到0.05mm；Z向加工误差达到0.08mm。

图8　不同平面度公差下机床加工误差分布图

选择平均值、方差、最大值和最小值典型统计参数分析机床三向加工误差随导轨形位公差的变化规律，如图9所示。在图9a中，随着导轨TA的增加，三向误差的平均值变化不是很明显；三向误差的标准差逐渐线性增加，即误差的分布范围逐渐增加，而且Z向离散程度更大一些。在图9b中，可以看出随着导轨平面度公差的增加，三向误差的最大值呈线性增加，最小值呈线性减小，其中Z向加工误差的最大值比X向和Y向的加工误差最大值大。

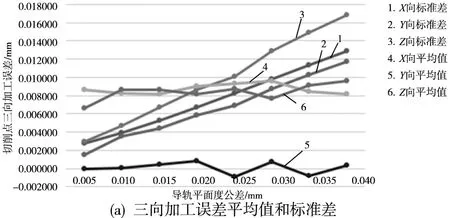
图9　机床加工误差典型参数变化情况

为了比较机床三向加工误差的敏感性，本文引入变异系数CV来比较平均值不同的观测样本的敏感性，其计算公式是样本标准差与平均值的比值：

(23)

变异系数越大，敏感性越高。根据公式，机床三向加工误差的变异系数随着TA的变化情况如图10所示。可以看出，虽然Z向误差的标准差更大一些，但是Y向的变异系数明显大于X和Z向，即Y向加工误差离散程度更明显，敏感性更高。

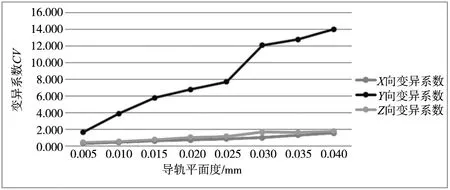
图10　机床三向加工误差敏感性分析

4.3　导轨平面度和垂直度公差的综合影响

机床加工误差的极值能够反映加工零件的合格率，探究导轨TA和TB对机床三向加工误差极值的综合影响，结果如图11所示。在图中，机床加工误差的极值正相关于导轨TA和TB，但从斜率分析导轨TA的影响程度更大。图11a中，X向最大加工误差达到了0.07mm；图11b中，Y向最大加工误差达到了0.05mm; 图11c中，Z向最大误差达到了0.09mm。

图11　导轨平面度和垂直度公差对机床加工误差的影响

4.4　导轨平行度和垂直度公差的综合影响

根据建立的机床加工误差不确定性模型，探究导轨TC和TB对机床加工误差极值的综合影响，结果如图12所示。可以看出，平行度公差和垂直度公差对加工误差有同等程度的影响作用，而且对Y向敏感方向影响作用不是很大。与图11对比可以看出，导轨TC和TB对机床三向误差的影响程度远不如导轨TA。因此，在保证加工误差的同时为了减轻零件的加工难度，可以适当的提高平行度和垂直度公差。

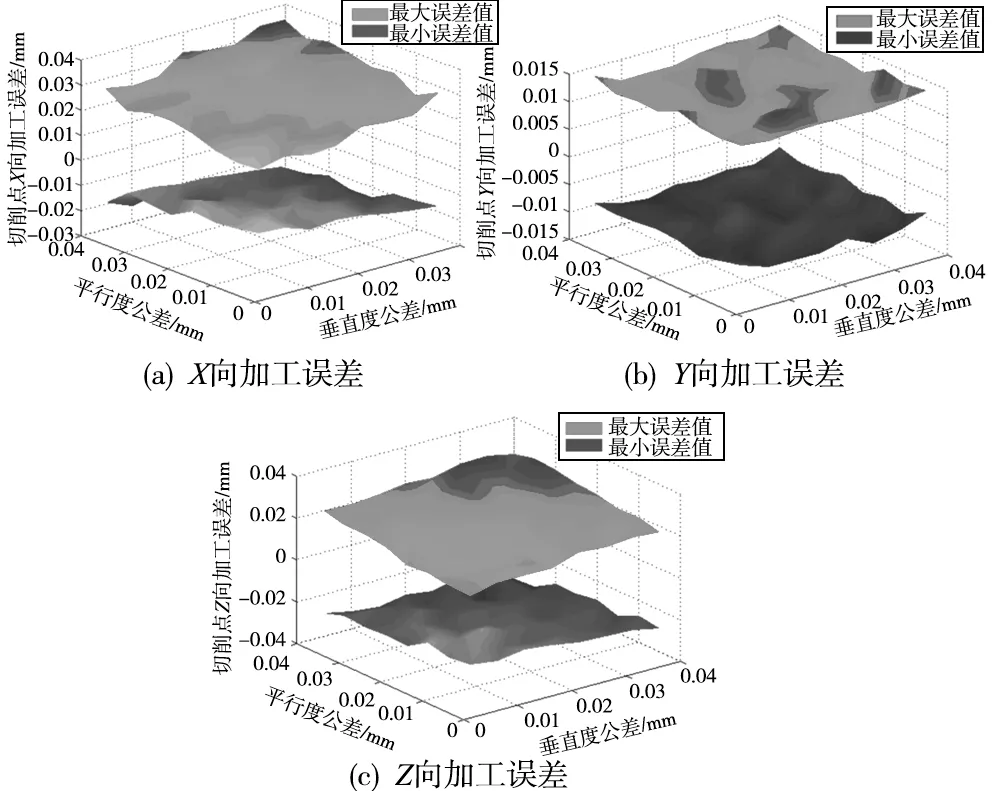
图12　导轨平行度和垂直度公差对机床加工误差的影响

5　结论

针对导轨形位误差不确定性的问题，本文提出了导轨形位误差不确定性分析方法，结合零部件运动误差的等效方法最终建立了基于导轨形位误差不确定性的机床加工误差分析模型。根据建立的模型，以某加工中心实例分析不同导轨形位公差对机床加工误差的影响规律，结果表明：导轨形位误差的不确定性会导致加工误差是不确定性的，使其分布在一定的区间内，且区间宽度几乎和形位公差呈线性变化的关系；平面度公差相比于垂直度和平行度公差对加工误差不确定性有较大程度的影响，根据分析可以为零部件的公差设计提供理论参考。

[参考文献]

[1] 程强, 刘广博, 刘志峰,等. 基于敏感度分析的机床关键性几何误差源识别方法[J]. 机械工程学报, 2012, 48(7):171-179.

[2] 粟时平. 多轴数控机床精度建模与误差补偿方法研究[D].长沙:国防科学技术大学, 2002.

[3] 王秀山, 杨建国, 闫嘉钰. 基于多体系统理论的五轴机床综合误差建模技术[J]. 上海交通大学学报, 2008, 42(5):761-764.

[4] Majda P. Modeling of geometric errors of linear guideway and their influence on joint kinematic error in machine tools[J]. Precision Engineering, 2012, 36(3):369-378.

[5] Rahman M, Heikkala J, Lappalainen K. Modeling, measurement and error compensation of multi-axis machine tools. Part I: theory[J]. International Journal of Machine Tools & Manufacture, 2000, 40(10):1535-1546.

[6] 马雅丽, 徐涛, 钱峰. 基于粒子群算法的机床支承件不确定性多目标优化[J]. 组合机床与自动化加工技术, 2017(1):1-5.

[7] 崔鑫磊, 李威. 基于蒙特卡洛模拟的6-UPS并联机构的误差分析[J]. 机械设计与制造, 2016(6):89-92.

[8] 余治民,刘子建,董思科,等.基于蒙特卡洛模拟与响应面方法的公差建模[J].中国机械工程, 2015, 26(4):427-434.

[9] ZHONG X, YANG R Q, ZHOU B. Accuracy Analysis of assembly success rate with Monte Carlo simulations[J]. Journal of Dong Hua University, 2003, 20(4):128-131.

[10] MAJDA P. Modeling of geometric errors of linear guideway and their influence on joint kinematic error in machine tools[J]. Precision Engineering, 2012, 36: 369-378.

(编辑李秀敏)