矩形b-度量空间中压缩映象的公共耦合不动点定理
刘丽亚,谷 峰
(杭州师范大学应用数学研究所;数学系,浙江杭州 310036)
1 引言和预备知识
Branciari[1]首次引入了矩形度量空间的概念,并给出了此空间中的Banach压缩映象定理.此后,很多学者在此空间中研究了其他不同压缩条件下的不动点问题[2−11],同时也给出了Banach压缩定理和Kannan型不动点定理在矩形b-度量空间中的一些应用.本文受到上述结论的启发,将在矩形b-度量空间中讨论耦合重合点和公共耦合不动点的存在性和唯一性问题,得到了一类新的公共耦合不动点定理,在很大程度上推广了相关文献[12]的一些结果.
在介绍主要结果之前,先介绍一些基本概念和已知结果.
定义1.1[1]设X 是非空集,d:X×X→[0,+∞),且∀x,y∈X,满足
(Rb1)d(x,y)=0当且仅当x=y;
(Rb2)d(x,y)=d(y,x);
(Rb3)d(x,y)≤s[d(x,u)+d(u,v)+d(v,y)],其中u,v∈X{x,y},同时u/=v.则称(X,d)为矩形b-度量空间,且s≥1为矩形b-度量空间(X,d)的系数.
注1.1[13]每个度量空间都是矩形b-度量空间,每个矩形度量空间也为矩形b-度量空间(这时s=1).反之不一定成立.
定义1.2[13]设{xn}是矩形b-度量空间(X,d)中的序列.{xn}称为X 中的Cauchy列,如果
定义1.3[13]设{xn}是矩形b-度量空间(X,d)中的序列.{xn}称为X 中的收敛列,如果
定义1.4[13]矩形b-度量空间(X,d)称为完备的,如果X 中的每一Cauchy列都收敛于X中的某个点.
注1.2[13]矩形b-度量空间(X,d)中的数列的极限点不一定唯一,且收敛列不一定是Cauchy列.
定义1.5[14]称(x,y)∈X×X是映象F:X×X→X的耦合不动点,如果F(x,y)=x,F(y,x)=y.
定义1.6[15]称(gx,gy)∈X×X是映象对F:X×X→X和g:X→X的重合耦合点,如果F(x,y)=gx,F(y,x)=gy.这时,称(x,y)∈X×X 是映象对F:X×X→X 和g:X→X的耦合重合点.
定义1.7[15]称(x,y)∈X×X是映象对F:X×X→X和g:X→X的公共耦合不动点,如果F(x,y)=gx=x,F(y,x)=gy=y.
定义1.8[16]设X为一非空集.映象对F:X×X→X和g:X→X称为ω-相容的,如果当F(x,y)=gx且F(y,x)=gy,总有gF(x,y)=F(gx,gy).
定义1.9[17]设X是一非空集,是定义在X中的一偏序关系,函数T:X×X→X,g:X→X.T称为具有混合g-单调性质,如果T(x,y)关于x是g-单调不减的,关于y是g-单调不增的,即对任意的x,y∈X,有
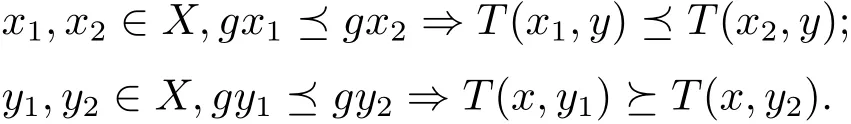
2 主要结果
为方便起见,下文中出现的函数ψ和φ均指满足以下条件的函数[19]:
(1)ψ:[0,∞)→[0,∞)满足:1)ψ是非减的且关于每个变元是连续的;2)ψ(t)=0当且仅当t=0.
(2)φ:[0,∞)→[0,∞)满足:1)φ是下半连续的;2)φ(t)=0⇔t=0.
定理2.1设(X,d)是一个矩形b-度量空间,其系数s>1,是定义在X上的一偏序.g:X→X为X上的自映象.映象T:X×X→X具有混合g-单调性.且满足以下条件
(1)T(X×X)⊆g(X);
(2)∃(x0,y0)∈X×X 使得gx0T(x0,y0),gy0T(y0,x0);
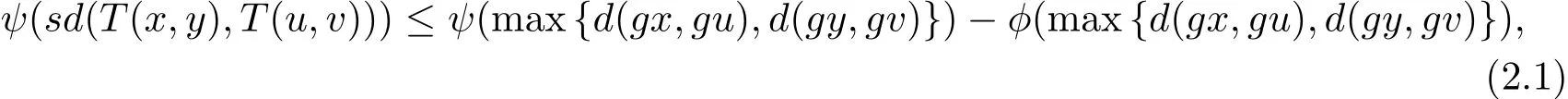
如果g(X)是(X,d)的完备子集,则g和T在X 中有重合耦合点.
证根据条件(2)可得,存在(x0,y0)∈X×X,使得gx0T(x0,y0),gy0T(y0,x0),由于T(X×X)⊆g(X),所以存在x1,y1∈X,使得gx1=T(x0,y0),gy1=T(y0,x0).类似的,存在x2,y2∈X,使得gx2=T(x1,y1),gy2=T(y1,x1).由于gx0T(x0,y0),gy0T(y0,x0),可得到gx0gx1,gy0gy1.由于映象T具有混合g-单调性,所以有依此类推,就可得到X 中的两个序列{xn}和{yn},使得gxn=T(xn,yn),gyn=T(yn,xn),并且{gxn}和{gyn}还满足
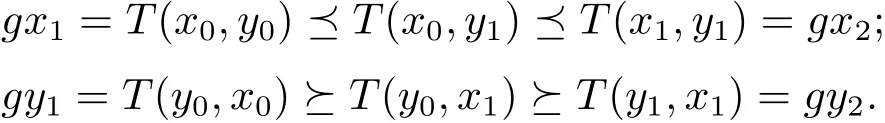
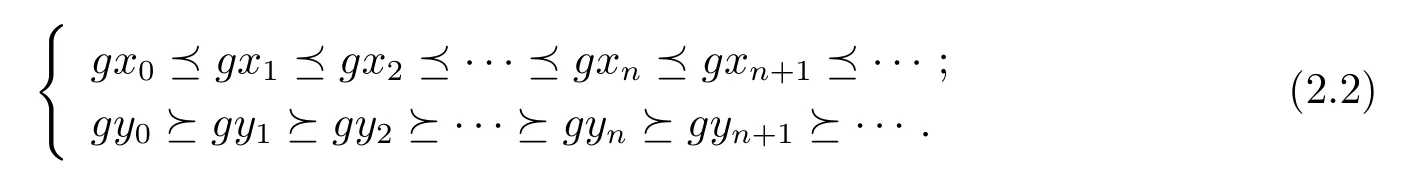
在式(2.1)中,取(x,y)=(xn,yn)和(u,v)=(xn+1,yn+1),并使用式(2.2)可得
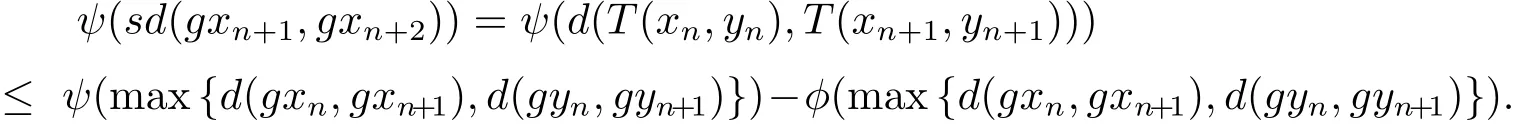
即
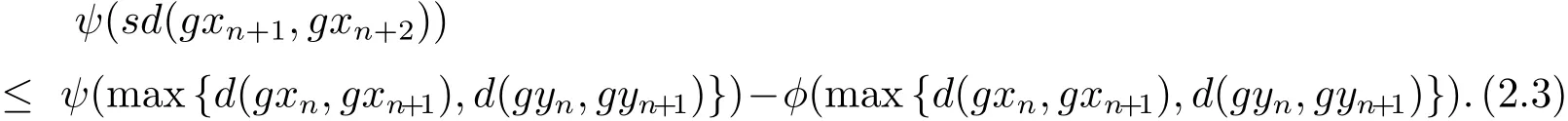
同理可得
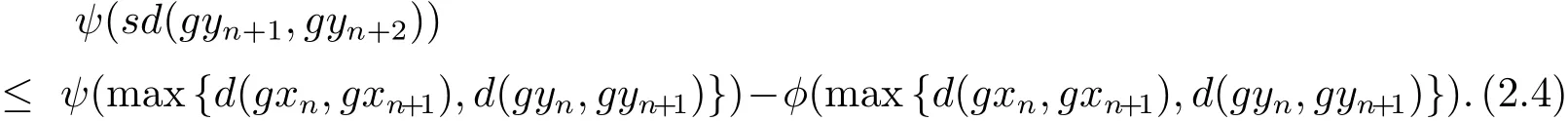
令
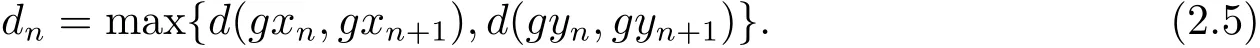
由于max{ψ(a),ψ(b)}= ψ(max{a,b}),∀a,b∈ [0,+∞),进而有
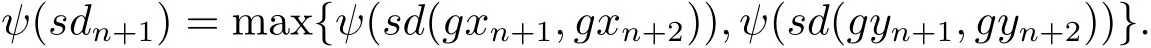
再根据(2.3),(2.4),(2.5)式和上式可得
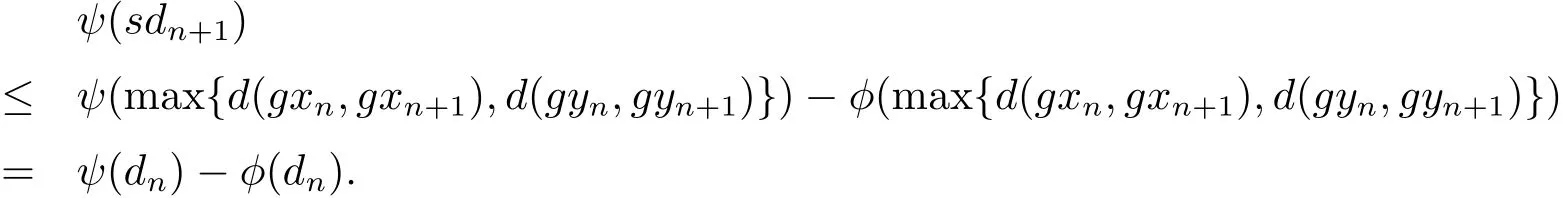
又由函数φ:[0,∞)→[0,∞),因此由上式可得
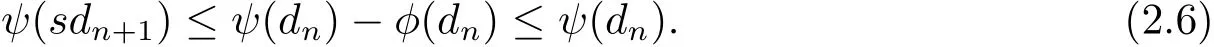
由ψ是非减的,可得

从而可知{dn}单调递减的非负实数列,因此存在r∈[0,∞),使得式(2.6)两边令n→∞ 时,取极限得ψ(sr)≤ψ(r)−φ(r)≤ψ(r).由ψ是非减的,可得sr≤r.又由s>1,所有当r>0时,出现矛盾,进而可得r=0.于是有由式(2.5)可知
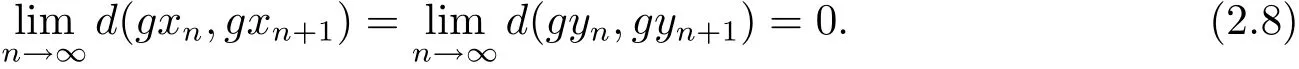
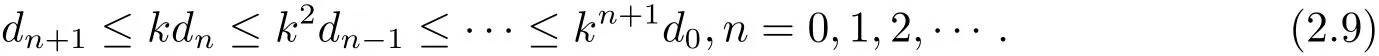
根据式(2.2),在式(2.1)中取(x,y)=(xn,yn)和(u,v)=(xn+2,yn+2),可得
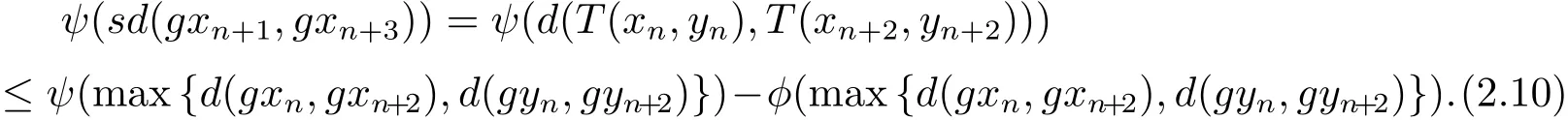
即
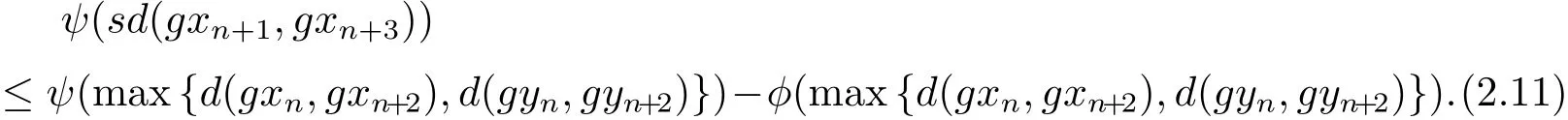
同理可得
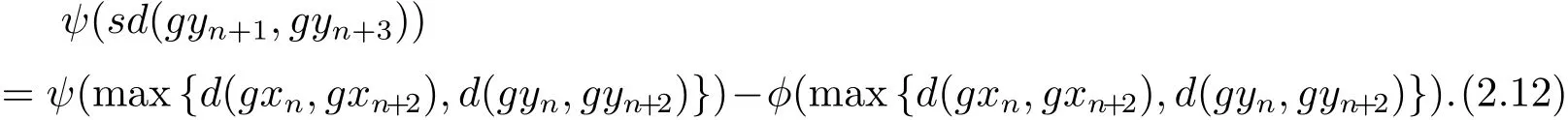
令
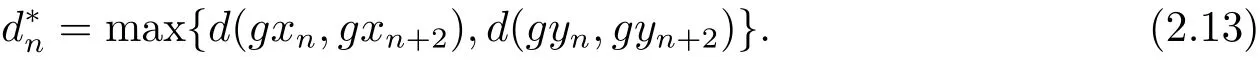
由于max{ψ(a),ψ(b)}= ψ(max{a,b}),∀a,b∈ [0,+∞),进而有
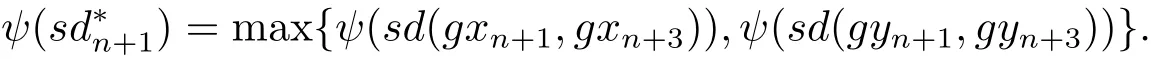
再根据 (2.11),(2.12) 和 (2.13) 式可得又由 ψ 是非减的可知又由可知依次类推可得到
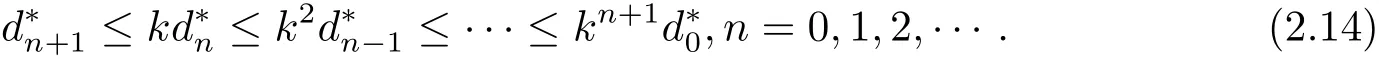
接下来,将证明{gxn}和{gyn}都是gX 中的Cauchy列.
a)当p是奇数时,设p=2m+1.
事实上,由性质(Rb3)可得
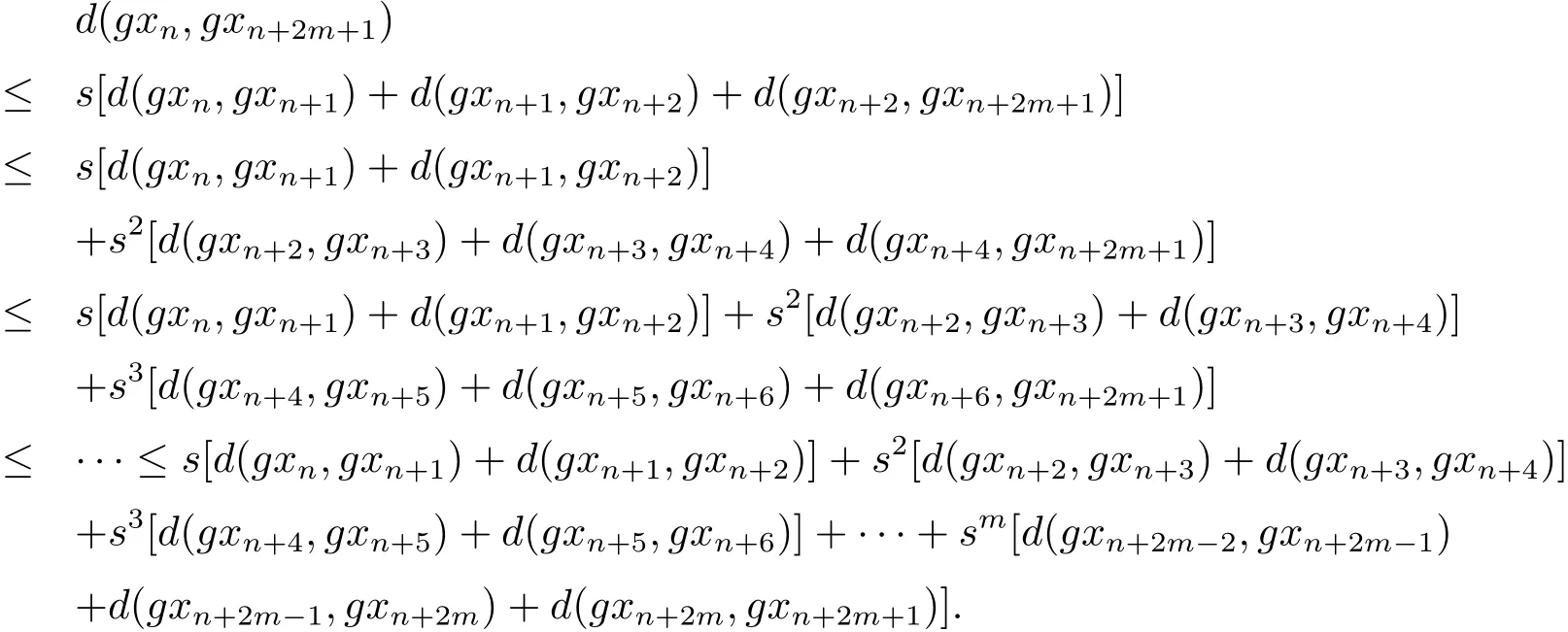
上式即
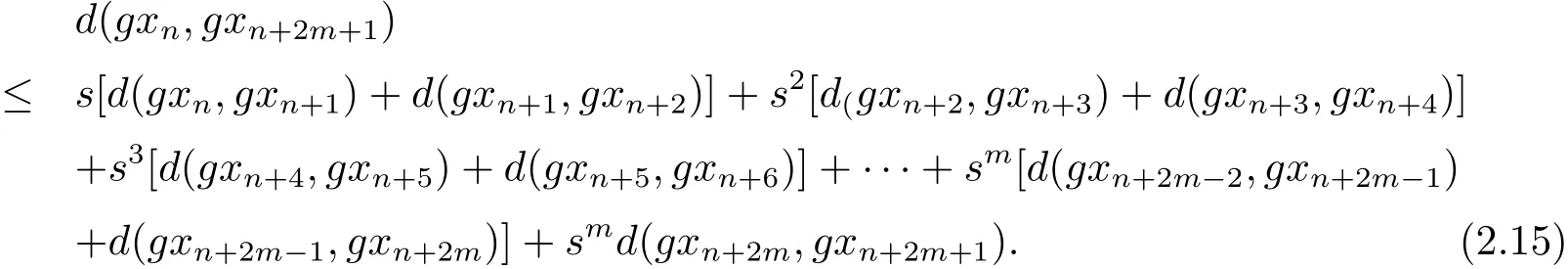
同样道理可知
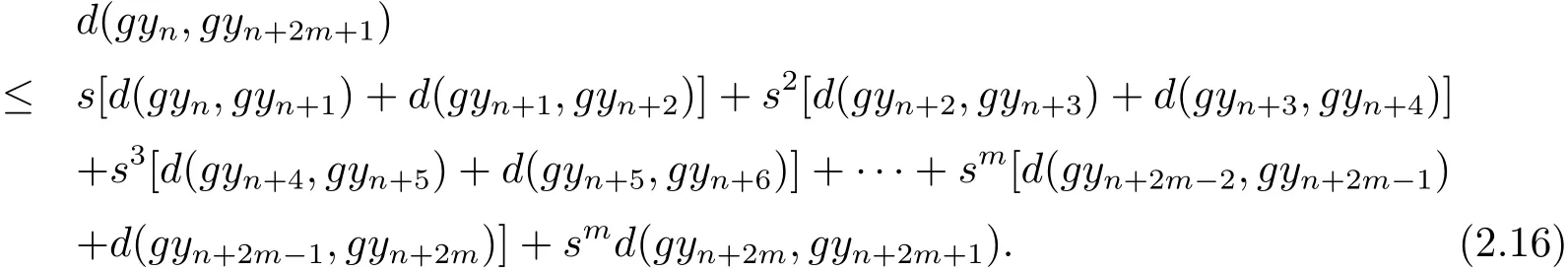

即
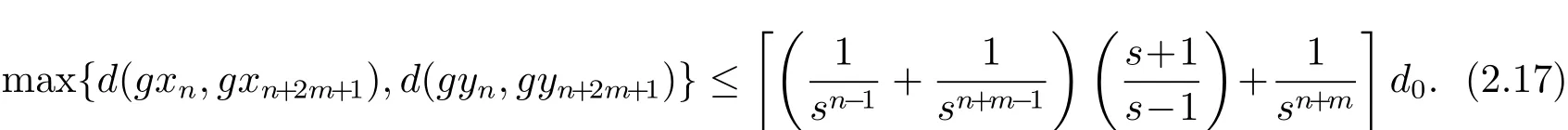
b)当p是偶数时,设p=2m.使用性质(Rb3)可得
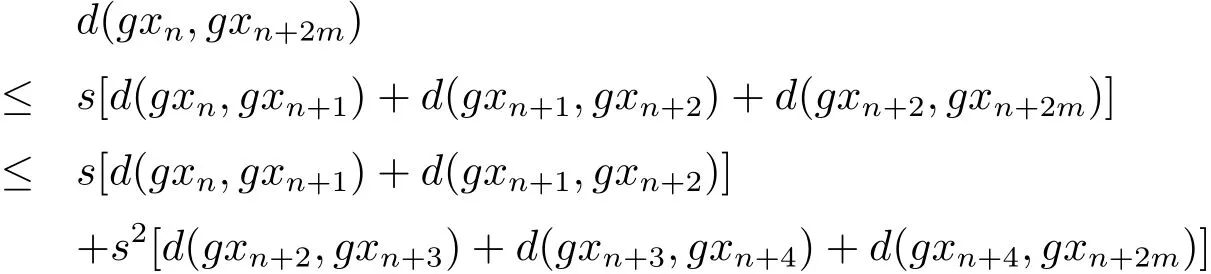
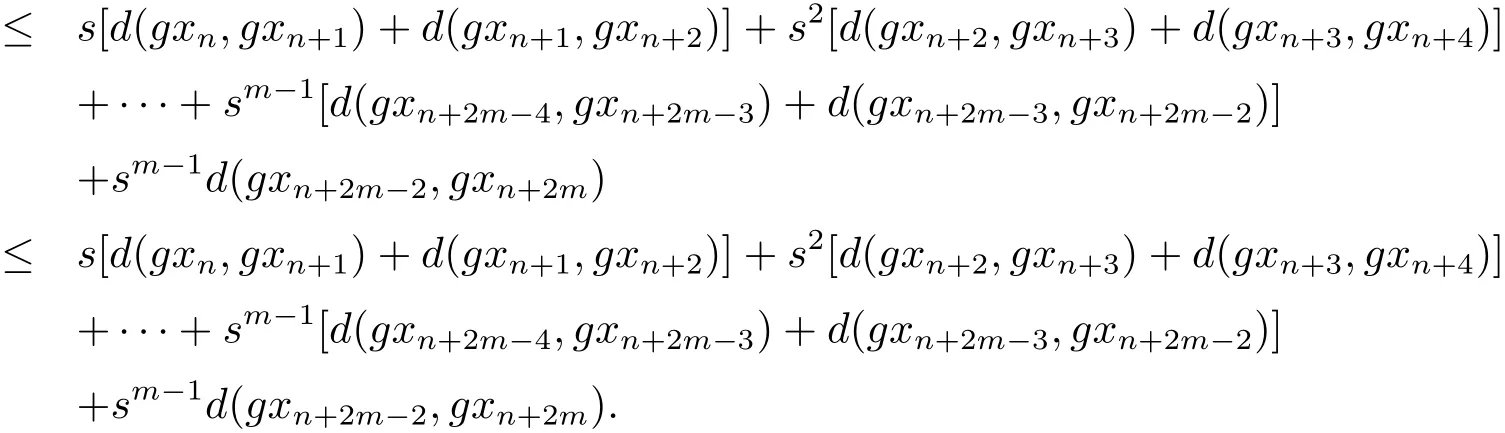
即
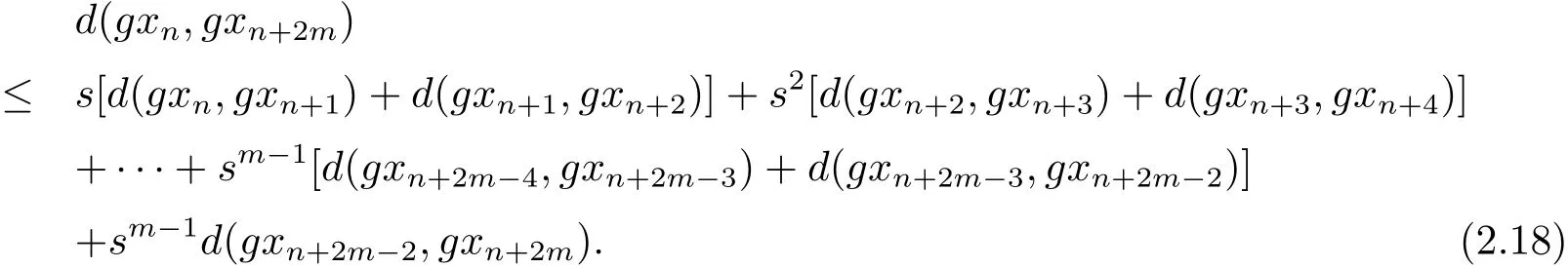
同样道理可知
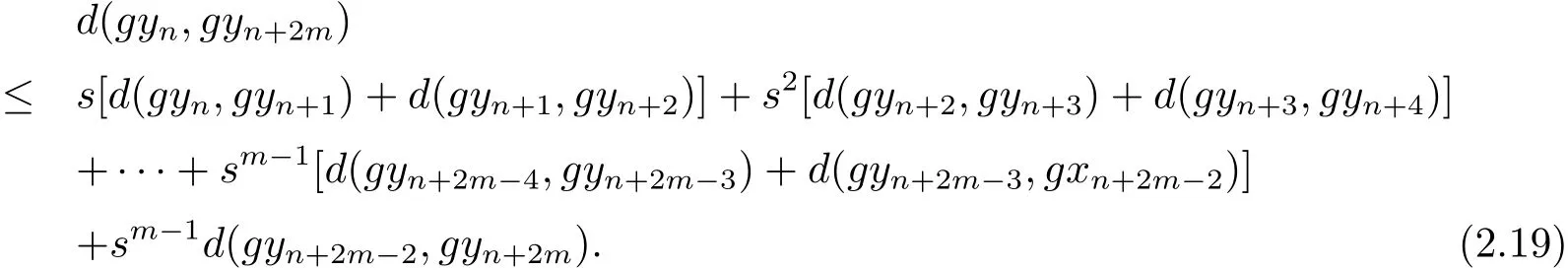
结合式(2.9),(2.14),(2.18)和(2.19)式,又由可得

进而可知
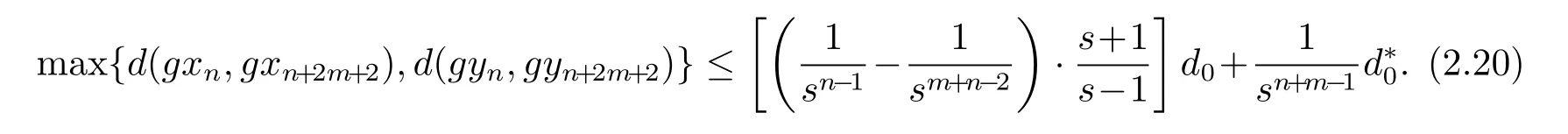
由(2.17)和(2.20)式可得
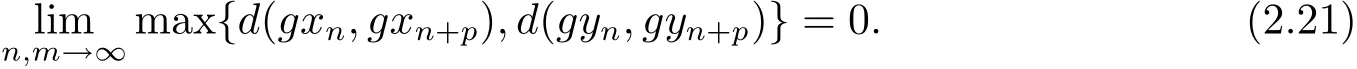
从(2.21)式可知{gxn}和{gyn}是g(X)中的Cauchy列.
又因为g(X)在是矩形b-度量空间(X,d)的完备子集,所以存在x,y∈X,使得
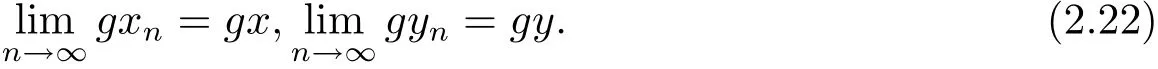
又由(2.1)式可得
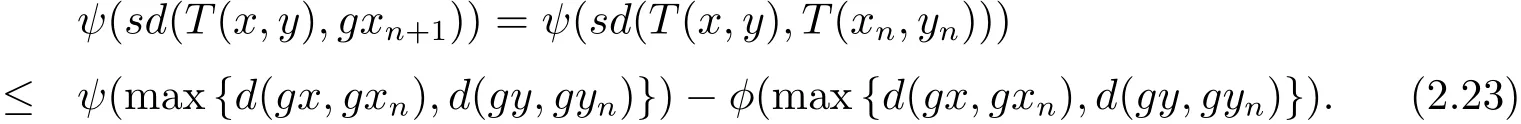
使用三角不等式
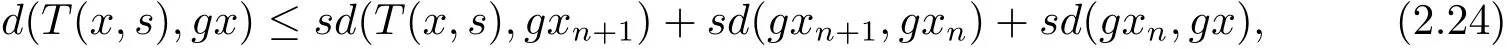
在(2.24)式中,令n→∞取极限,
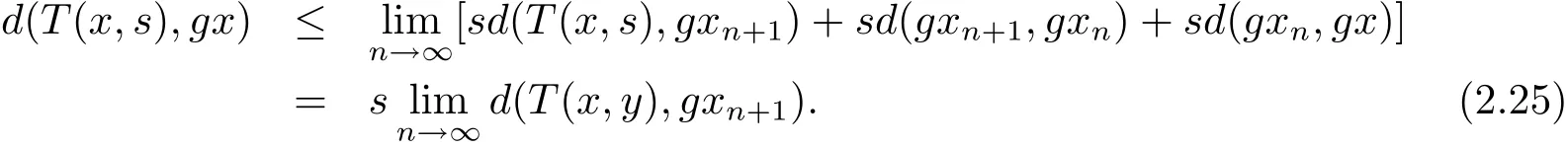
使用(2.22)和(2.25)式,在(2.23)式两边令n→∞取极限,可得
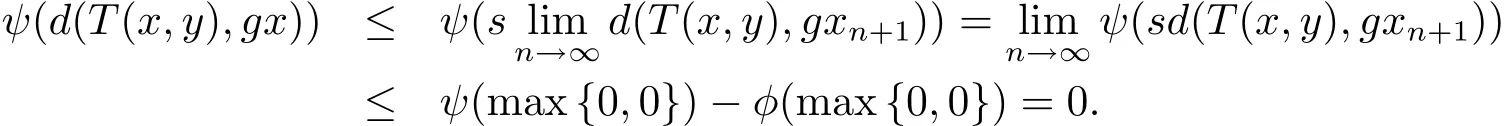
即d(T(x,y),gx)=0,进而可知T(x,y)=gx.同理可得T(y,x)=gy.从而有(gx,gy)是g和T的重合耦合点,证毕.
定理2.2设(X,d)是矩形b-度量空间,其系数s>1,是定义在X 上的一个偏序.g:X→X为X上的自映象.映象T:X×X→X具有混合g-单调性.且满足以下条件
(1)T(X×X)⊆g(X);
(2)∃(x0,y0)∈X×X 使得gx0T(x0,y0),gy0T(y0,x0);
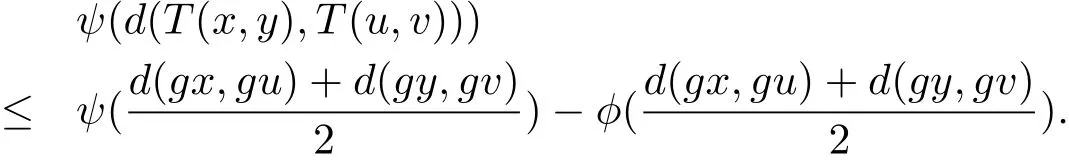
如果g(X)是(X,d)中的完备集,则g和T在X 中有重合耦合点.
证与定理2.1证明方法相同,略去.
注2.1令定理2.1中的自映象g为恒等映象I,即有下面推论.
推论2.1设(X,d)是矩形b-度量空间,其系数s>1,是定义在X 上的一个偏序.映象T:X×X→X.如果满足以下条件
(1)∃(x0,y0)∈X×X 使得x0T(x0,y0),y0T(y0,x0);
则T在X中有耦合不动点.
注2.2∀a,b,c∈[0,+∞),有
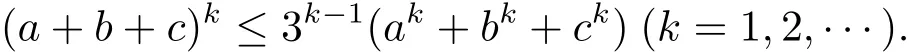
证显然当k=1,2时结论成立,假设当k=m时结论成立,即
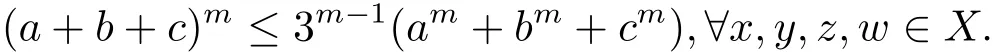
现证当k=m+1时结论也成立.事实上,有
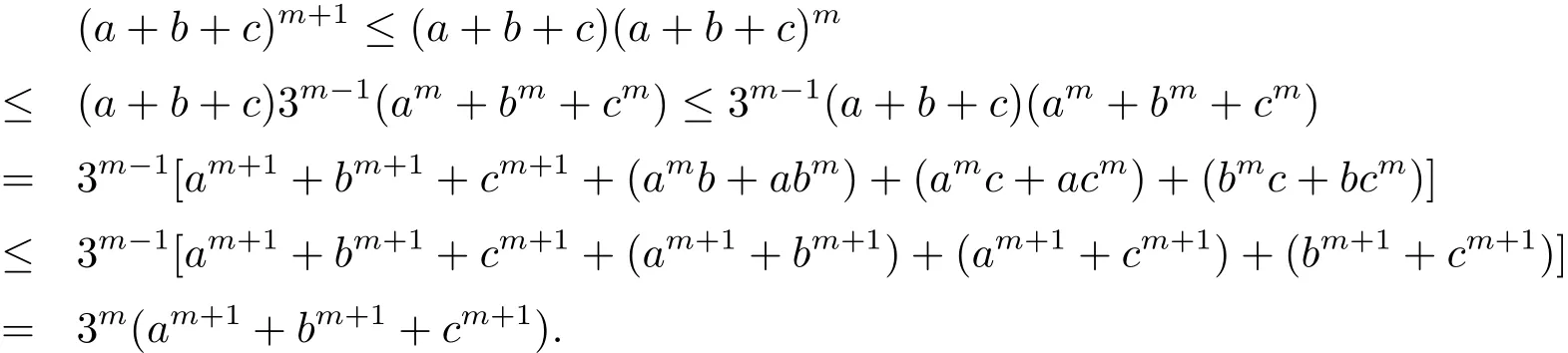
从而结论对一切自然数k成立.
例2.1设X=R,∀x,y∈X,定义d(x,y)=(x−y)2,则(X,d)是一个系数s=3的矩形b-度量空间.设X上的偏序关系定义如下:xy⇔x≤y.定义函数T:X×X→R+和g:X→R+分别如下
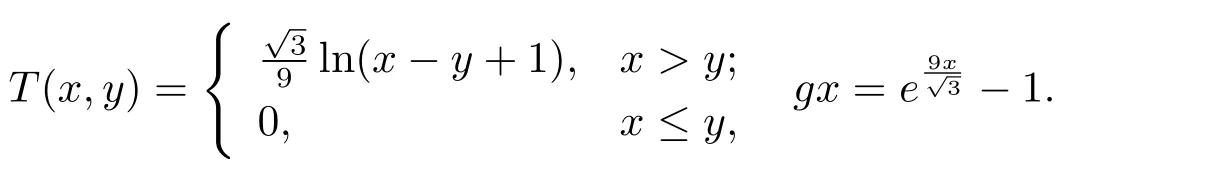
易得T(X×X)⊆g(X),且T具有g-混合单调性.当
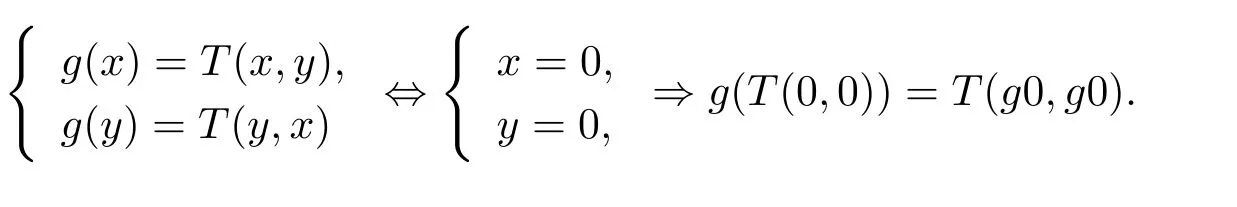
即F和g是ω-相容的.令(x,y)=(0,0)时,这时有g0T(0,0),g0T(0,0).
定义函数ψ,φ:R+→R+分别为
下面分四种情况讨论.
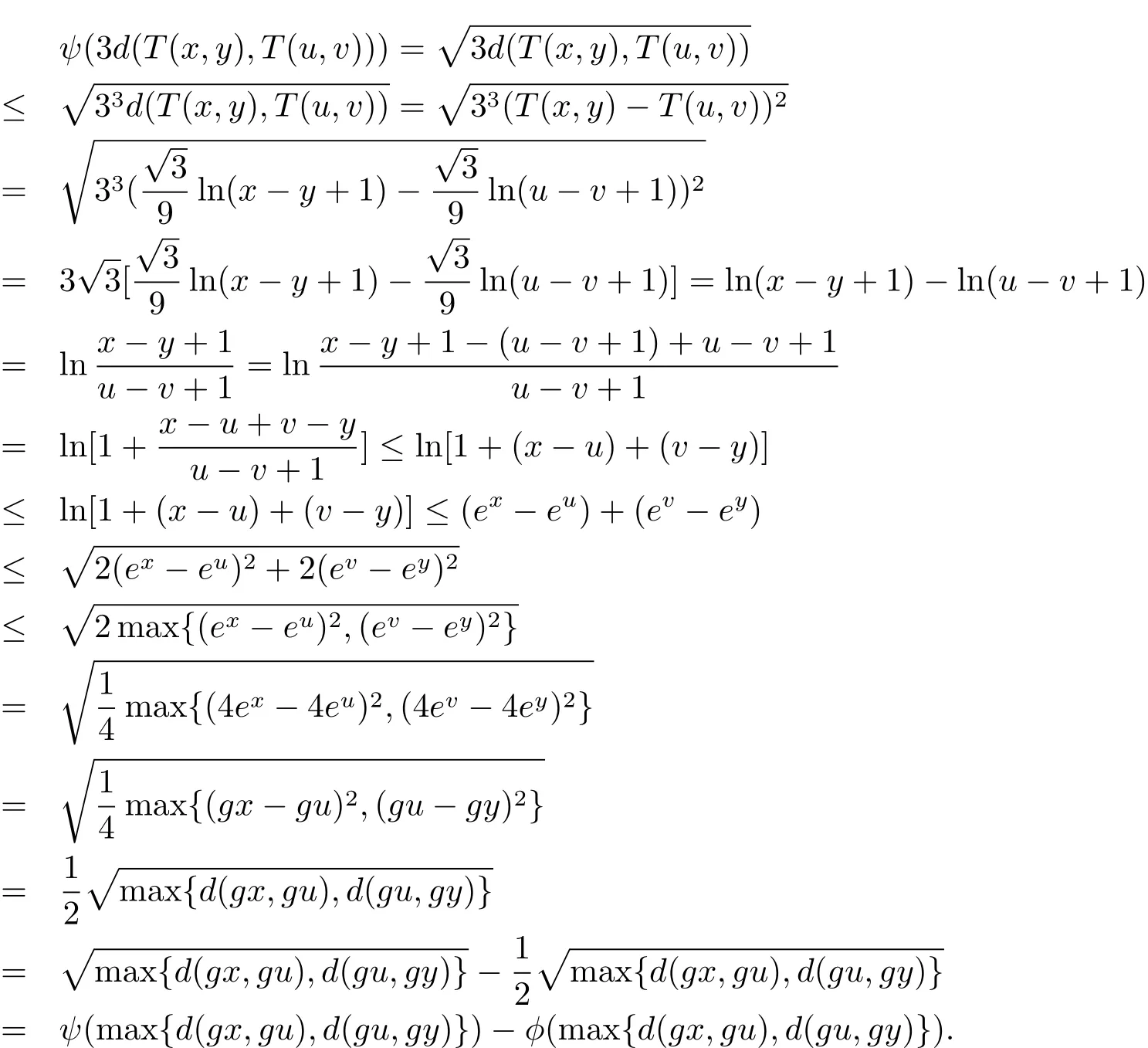
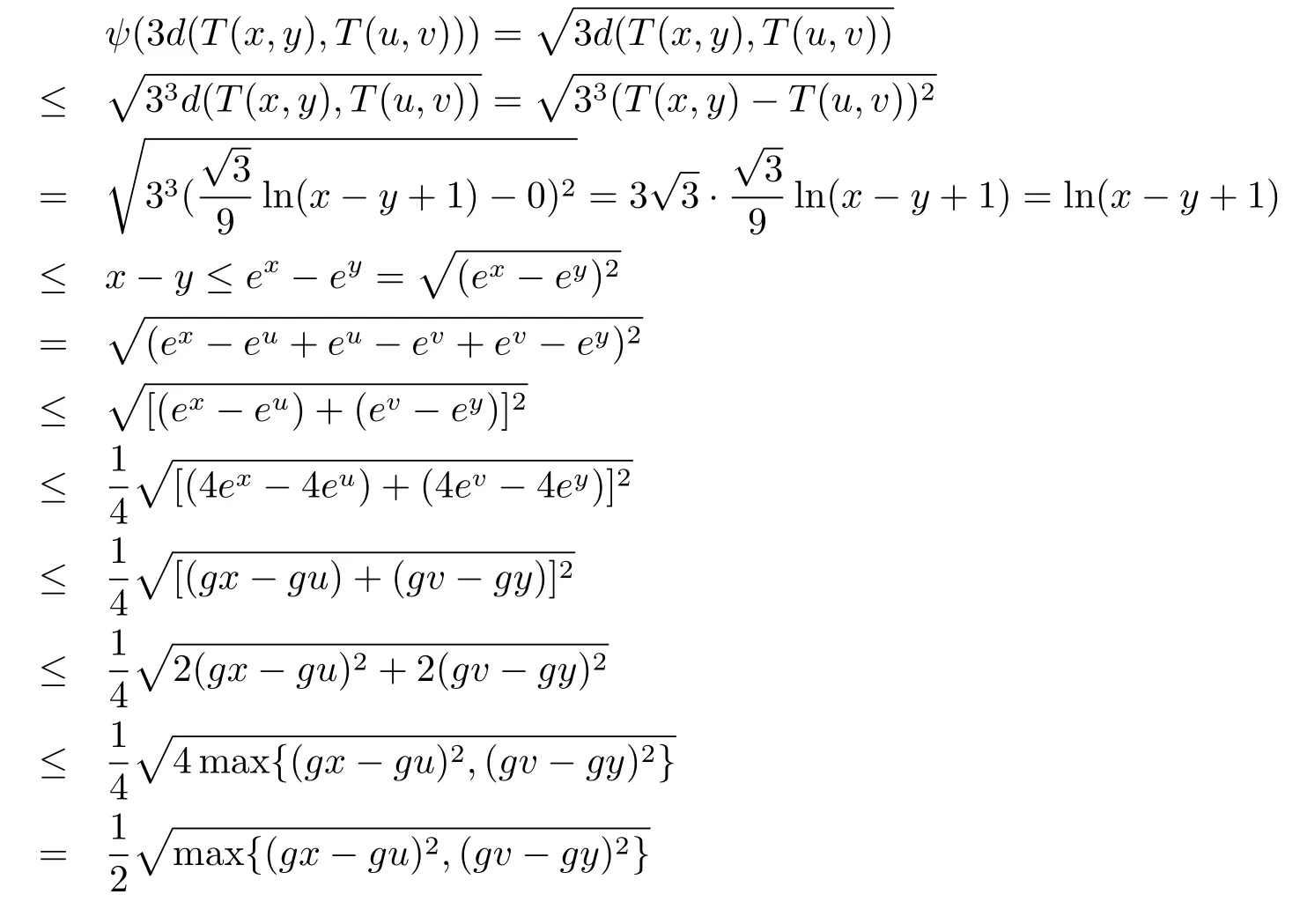
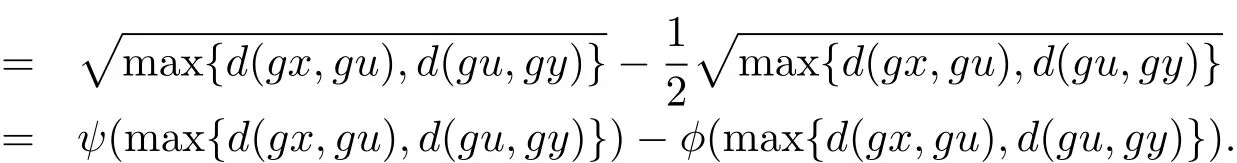
4)当T(x,y)=0,T(u,v)=0时,即x≤y,u≤v时,显然成立.
从而根据定理2.1,可证得T和g具有耦合重合点,且T(0,0)=g0=0.
3 不动点的唯一性
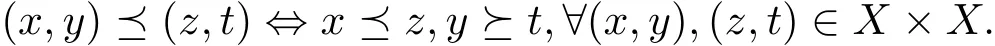
定理3.1在定理2.1的条件下,假设g和T是ω-相容的,且g和T的任意两个重合耦合点(gx∗,gy∗)和(gz∗,gt∗)都有相应的公共可比较点(gu∗,gv∗)∈ X ×X,这时g和T 有唯一的耦合公共不动点.
证由定理2.1可知g和T至少存在一个重合耦合点.不妨假设(x,y),(z,t)∈X×X是g和T的任意两个耦合重合点,即T(x,y)=gx,T(y,x)=gy和T(z,t)=gz,T(t,z)=gt.现证(gx,gy)=(gz,gt).
由已知条件可知,存在(u,v)∈X×X,使得(gu,gv)分别和(gx,gy),(gz,gt)都可比较.
a)当可比较关系为
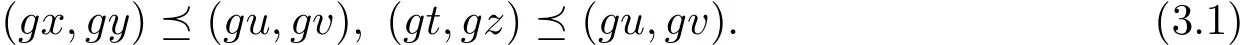
令
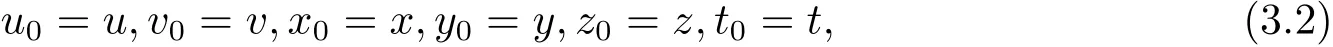
则∃(u1,v1)∈X×X,使得
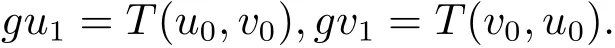
依次类推,会得到两个数列{gun}和{gvn}分别为
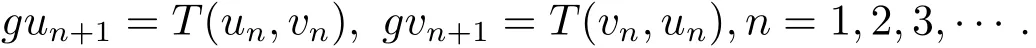
同样道理,可以得到数列{gxn},{gyn}和{gzn},{gtn}分别为
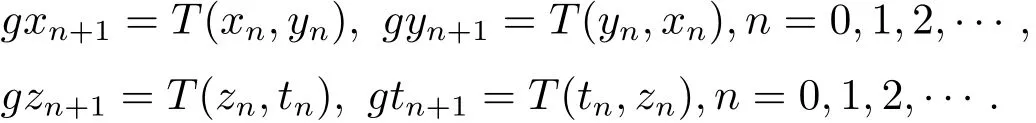
由于(x,y)是g,T的耦合重合点,则有
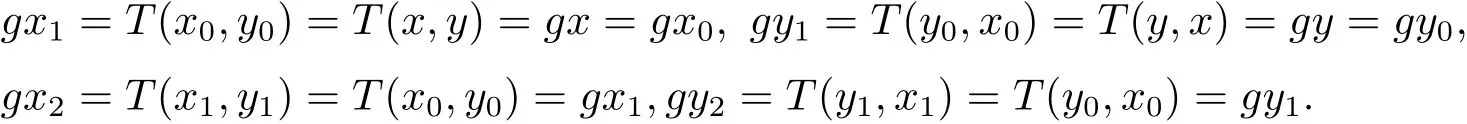
依次类推可知 gx0=gx1= ···=gxn= ···,gy0=gy1= ···=gyn= ···.即
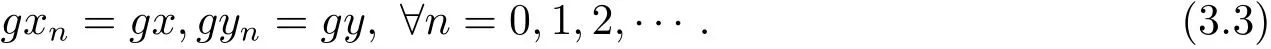
相同道理可知
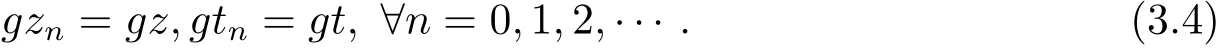
由于(3.1)和(3.2)式可得

由于T具有混合g-单调性,所以可得
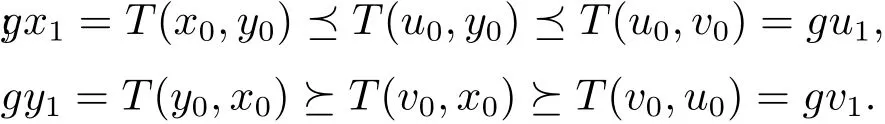
即(gx1,gy1)(gu1,gv1).同理可得(gx2,gy2)(gu2,gv2).这样继续做下去,可得
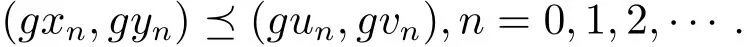
类似方法,可得
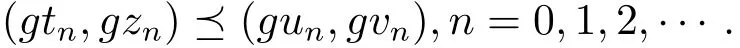
结合(3.3)和(3.4)式可得
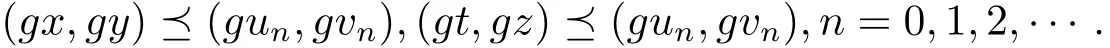
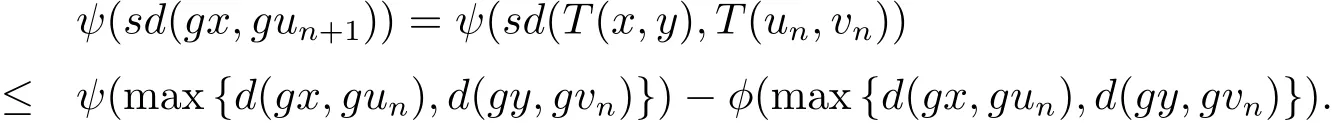
即
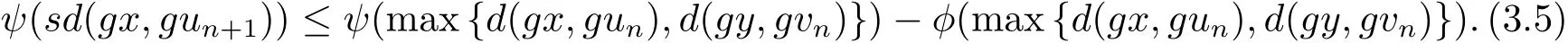
同理可得
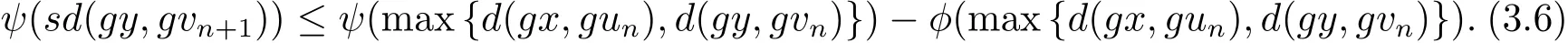
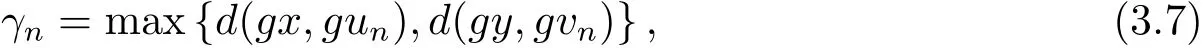
现令联立(3.5),(3.6)和(3.7)式,又由max{ψ(a),ψ(b)}= ψ(max{a,b}),∀a,b∈ [0,+∞),可得到
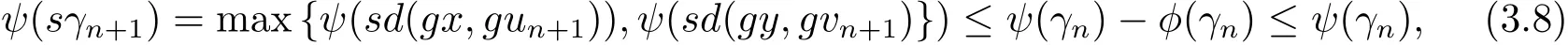
从而可得γn+1≤γn.所以可知{γn}单调递减的非负实数列,存在r∈X,使得r≥0且因为将上式两边令 n → ∞ 时,取极限得ψ(sr)≤ψ(r)−φ(r).当r>0时,出现矛盾.即r=0.于是有
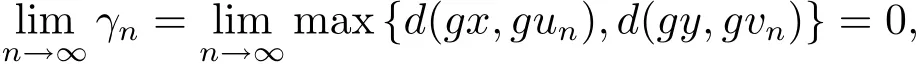
进而可知
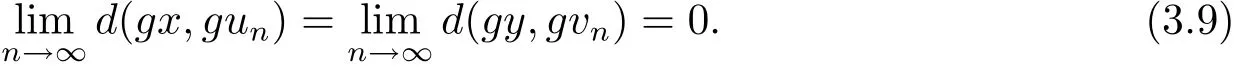
同样道理可证得
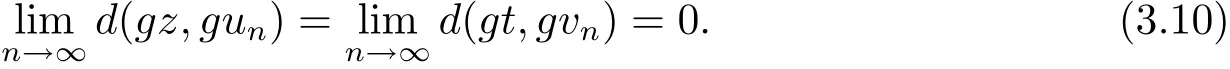
由(3.9)和(3.10)式可得到
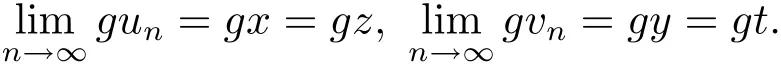
即(gx,gy)=(gz,gt).所以g和T具有唯一的重合耦合点.又因为g和T是ω-相容的,得到
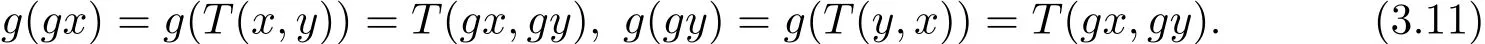
由于∃m,n∈X,使得gx=m,gy=n,那么(3.12)式可整理为

因此(m,n)也是g和T的一个耦合重合点,由重合耦合点的唯一性知gm=gx=m,gn=gy=n.又由(3.12)式可得m=gm=T(m,n),n=gn=T(n,m).即证得g和T有耦合公共不动点.由于g和T的重合耦合点具有唯一性,因此g和T的耦合公共不动点也具有唯一性.
同a)的证明方法类似,上述三种情况同样也能证得g和T的耦合公共不动点也具有唯一性.
4 在积分方程中的应用
假设X=C[a,b]是定义在[a,b]上的连续函数全体.≤是定义在X 上的偏序关系,定义

定义d:X×X→R+为
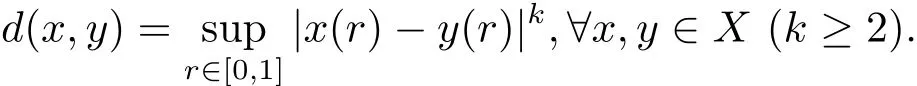
这时易知(X,d)是一个完备的矩形b-度量空间,由注2.2可知,其系数s=3k−1.
考虑以下积分方程组问题
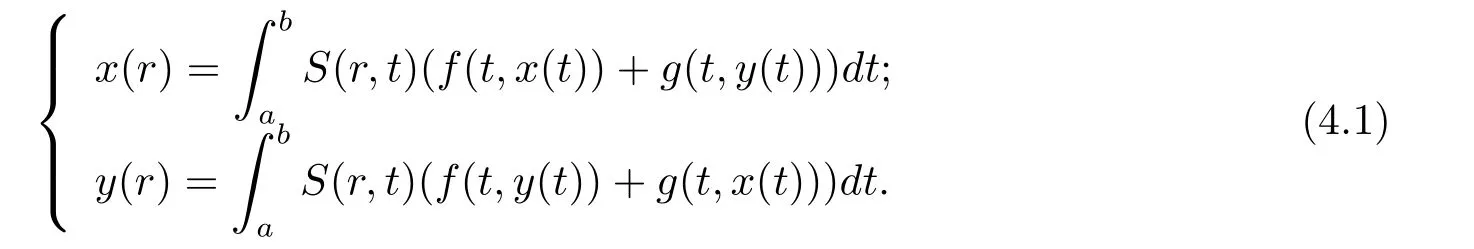
接下来,假设下面几个条件成立.
(i)S(r,t):[a,b]×[a,b]→R+是连续函数.
(ii)f,g:[a,b]×R→R是连续函数.
(iii) ∃(x0,y0)∈X×X,使得
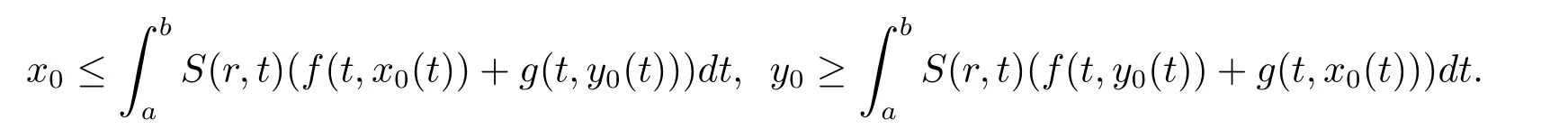
(iv)∃µ,ν使得对于任意的r∈[a,b],x,y∈R,有
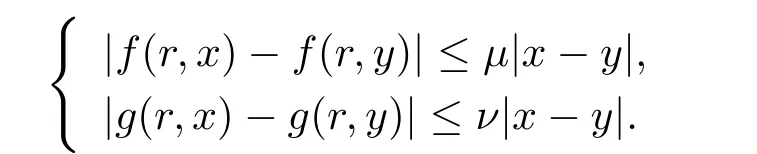
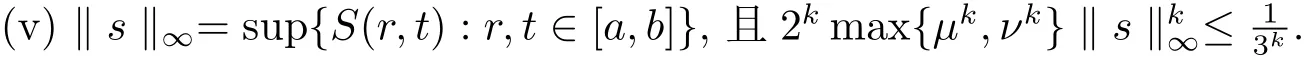
定理4.1由上述条件(i)–(v)成立,则积分方程组(4.1)有唯一的解.
证构造函数T:X×X→X和g:X→X如下
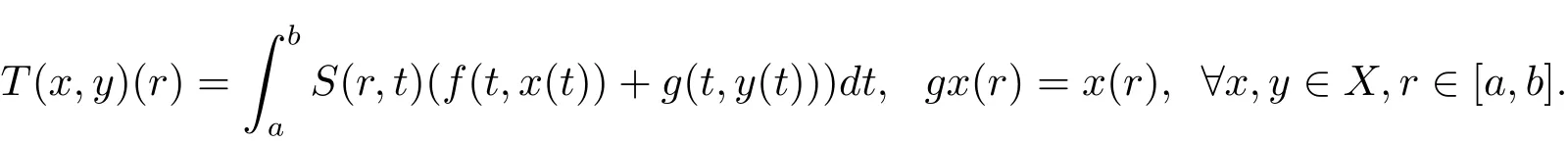
则由条件(iii)可知gx0T(x0,y0),gy0T(y0,x0),且g和T具有ω-相容性.又由条件(iv)和(v)可得
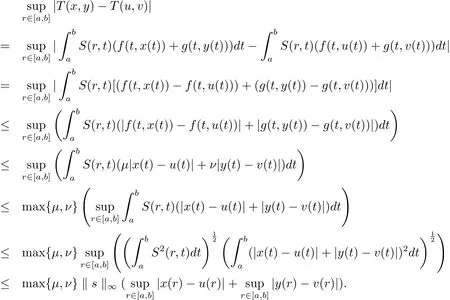
于是由条件(v),上式可整理为
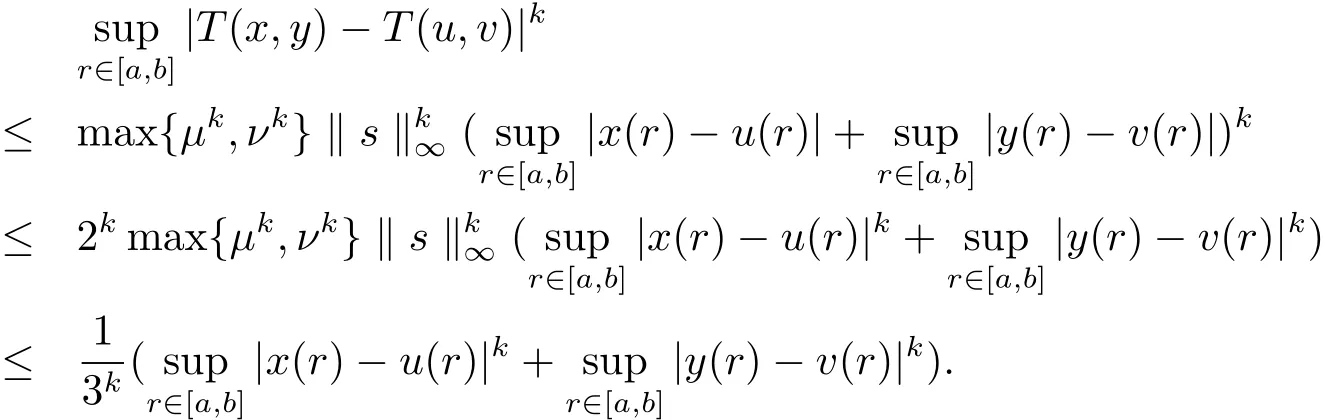
上式即为
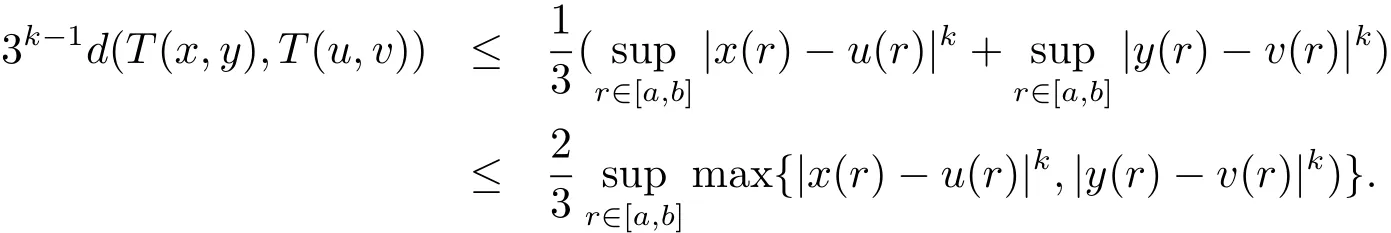
于是
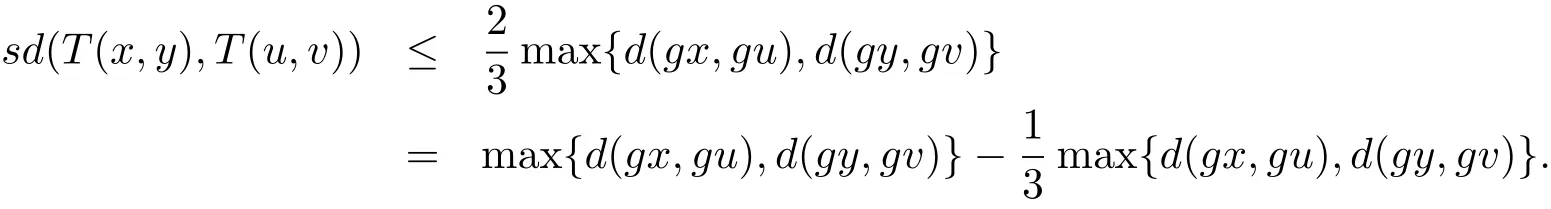
令函数ψ,φ:R+→R+分别为那么上式即为
ψ(sd(T(x,y),T(u,v)))≤ ψ(max{d(gx,gu),d(gy,gv)})−φ(max{d(gx,gu),d(gy,gv)}).由此易知定理3.1的所有条件被满足,于是,存在(x∗,y∗)∈X×x,使得
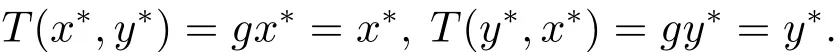
即(x∗,y∗)也为方程组(4.1)在C[a,b]上的唯一解.
[1]Bakhtin I A.The contraction mapping principle in quasimetric spaces[J].Funct.Anal.,Unianowsk Gos.Ped.Inst.,1989,30:26–37.
[2]Azam A,Arshad M.Kannan fixed point theorems on generalized metric spaces[J].J.Nonl.Sci.Appl.,2008,1:45–48.
[3]Azam A,Arshad M,Beg I.Banach contraction principle on cone rectangular metric spaces[J].Appl.Anal.Disc.Math.,2009,3:236–241.
[4]Chen C M.Common fixed point theorem in complete generalized metric spaces[J].J.Appl.Math.,Article ID 945915,2012.
[5]Das P.A fixed point theorem on a class of generalized metric spaces[J].Korean J.Math.Sci.,2002,9:29–33.
[6]Das P,Dey L K.A fixed point theorem in generalised metric spaces[J].Soochow J.Math.,2007,33(1):33–39.
[7]Lahiri B K.Das,P.Fixed point of a Ljubomir Ciric’s quasi-contraction mapping in a generalized metric space[J].Publ.Math.Debrecen,2002,61(3-4):589–594.
[8]Das P,Lahri B K.Fixed point of contractive mappings in a generalised metric space[J].Math.Slovaca,2009,59(4):499–504.
[9]Erhan I M,Karapinar E,Sekuli´c T.Fixed points of(ψ,φ)contractions on rectangular metric spaces[J].Fixed Point Theory Appl.,2012,138,DOI:10.1186/1687-1812-2012-138.
[10]Lakzian H,Samet B.Fixed points for(ψ,φ)-weakly contractions mapping in generalized metric spaces[J].Appl.Math.Lett.,2012,25(5):902–906.
[12]魏利,周海云.Banach空间中有限个增生算子公共零点的带误差项的迭代格式[J].数学杂志,2009,29(3):329–334.
[12]Gu F.Some new common coupled fixed point results in two generalized metric spaces[J].Fixed Point The.Appl.,2013,2013:181,DOI:10.1186/1687-1812-2013-181.
[13]Branciari A.A fixed point theorem of Banach-Caccippoli type on a class of generalized metric spaces[J].Publ.Math.Debrecen,2000,57:31–37.
[14]Bhaskar T G,Lakshmikantham V.Fixed point theorems in partially ordered metric spaces and applications[J].Nonl.Anal.,2006,65:1379–1393.
[15]Lakshmikantham V,´Ciri´c L B.Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces[J].Nonl.Anal.,2009,70:341–4349.
[16]Abbas M,Khan M A,Radenov´ıc S.Common coupled fixed point theorem in cone metric space for ω-compatible mappings[J].Appl.Math.Comput.,2010,217:195–202.
[17]Berinde V,Borcut M.Tripled fixed point theorems for contractive type mappings in partially ordered metric spaces[J].Nonl.Anal.,2011,74(15):4889–4897.
[18]谷峰.不动点定理与非线性算子迭代序列的收敛性[M].哈尔滨:黑龙江科技出版社,2002.

