基于群体平衡理论的管内水合物沉积特性数值模拟

宋光春，李玉星，王武昌，姚淑鹏，魏 丁，闫 斌

（1.山东省油气储运安全省级重点实验室 中国石油大学（华东），山东 青岛 266580；

2.泰能天然气有限公司，山东 青岛 266580；3.烟台新奥燃气发展有限公司，山东 烟台 264002）

水合物颗粒在油气输送管线内的着床沉积是导致管线堵塞的重要原因［1］，因此，研究管道内水合物的沉积特性对深水流动安全保障具有十分重要的意义［2-3］。目前，环道实验是研究管道内水合物沉积特性的主要方法［4］。近年来，随着计算流体力学（CFD）的发展，数值模拟已成为替代环道实验进行水合物沉积特性研究的有效手段。

Jassim等［5］使用CFD的方法研究了水合物在输气管线内的沉积特性并建立了相应的沉积位置计算模型，但该模型并未实现水合物颗粒与流场的直接耦合。魏丁等［6］使用Fluent软件耦合固液两相流并以此模拟水合物颗粒在管线内的沉积，模拟结果表明，流速对水合物沉积过程影响显著，当流速达到一定值时，水合物体积分数对水合物沉积过程的影响不再重要。采用同样的方法，陈鹏等［7-10］研究了流速、水合物体积分数、水合物颗粒粒径、水合物颗粒黏度、壁面条件及管径等因素对水合物沉积层高度的影响。但上述所有模拟均未考虑水合物颗粒粒径的变化。Fatnes等［11］通过引入水合物颗粒聚集粒径模型［12］计算水合物颗粒粒径的变化并使用ANSYS CFX模拟了弯管处水合物的沉积情况，但该模型取水合物颗粒间的聚集力为常数且并未考虑颗粒间的聚并效率。Balakin等［13］使用群体平衡模型与CFD相结合的方法模拟了水合物在管道内的聚集和沉积特性，该方法较全面地考虑了水合物颗粒在流动过程中的聚集和破碎，模拟结果与工程实际最接近。因此，群体平衡模型-CFD方法是对管道内水合物颗粒沉积特性进行数值模拟的有效方法。

本工作引入了基于水合物颗粒聚集动力学的群体平衡模型，通过碰撞频率和聚并效率分析水合物颗粒间的聚集，通过破碎频率和破碎后子颗粒的粒径分布函数分析水合物颗粒的破碎。利用Fluent 14.5软件，对固液两相流模型和群体平衡模型进行耦合求解，进而模拟流速、水合物颗粒粒径及水合物体积分数对管内水合物颗粒沉积特性的影响。

1 数值模型

1.1 几何模型

为了精确模拟水合物在水平圆管内的沉积特性，参考文献［14］所用实验环道建立了三维水平圆管模型（见图1），管道长度为3 m，内径为45.2 mm。对几何模型进行六面体网格划分，进口壁面以1 mm为步长进行划分；在近壁面处，为了处理边界层效应，采用8层网格加密，其余网格均以1 mm为步长进行划分。本工作几何模型总计划分267 696个六面体网格，网格质量0.913。

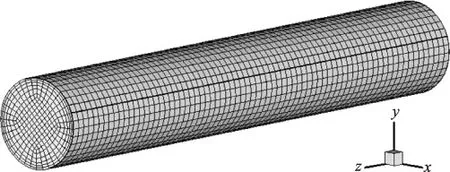
图1 水平圆管几何模型及网格划分示例Fig.1 Three-dimensional geometric model and mesh structure of the horizontal pipe.

对网格数量进行独立性检验，结果见图2。从图2可看出，当网格数分别为527 616和267 696个时，管流（流速2 m/s）充分发展段近壁面处速度梯度的相对偏差较小（6.3%），说明网格数量满足独立性要求。

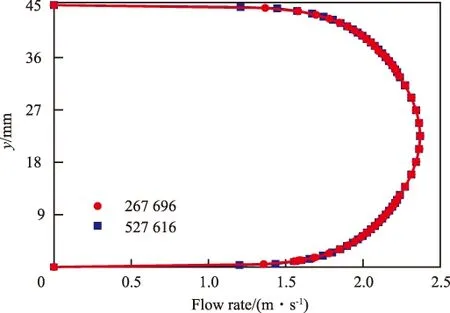
图2 网格独立性检验Fig.2 Grid dependency test.

1.2 多相流模型及湍流模型

本工作在建模过程中采用了以下假设：流动过程等温且忽略相间质量传递，即不考虑水合物的生成及分解；水合物浆由水相和水合物颗粒相构成，不考虑气相和油相；水合物颗粒粒径连续分布；不考虑水合物颗粒在管壁上的黏附过程。在上述假设下，本工作采用的物理模型主要包括多相流模型、湍流模型和群体平衡模型。其中，多相流模型采用欧拉-欧拉双流体模型，由连续性方程（见式（1））、动量方程（见式（2））两个控制方程和若干用于封闭方程组的本构方程构成。

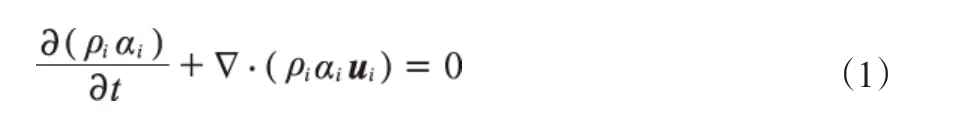
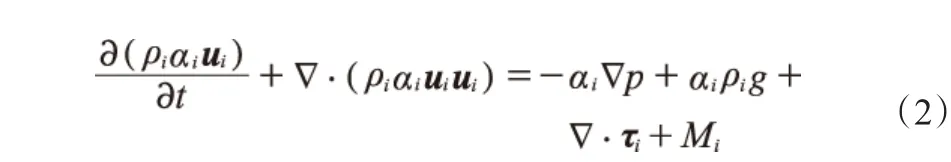
式中，i为水相或水合物颗粒相；t为时间，s；ρ为密度，kg/m3；α为体积分数，%；d为拉普拉斯算子；u为速度矢量，m/s；p为压力，Pa；τi为应力张量，Pa；Mi则为相间动量交换项，kg/（m·s）2。

水合物浆的液固耦合是多相流模型建立时考虑的重点，在模拟过程中，液固耦合通过相间动量交换实现。在计算Mi时，主要考虑相间拖曳力（Mdi）和湍流扩散力（Mti），并以此建立相间作用力模型以封闭多相流模型，见式（3）。

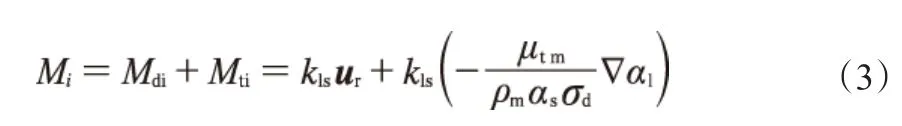
式中，ur为相间相对流速，m/s；μtm为湍流黏度，kg/（m·s）；σd为Planck扩散系数；αs为水合物体积分数，%；kls为动量传递系数，本工作采用Gidaspow模型［15］计算：当αs≤20%时，由Wen-Yu公式计算，见式（4）；当αs＞ 20%时，由Ergun公式计算，见式（5）。

式中，L为水合物颗粒粒径，m；μl为水相动力黏度，kg/（m·s）；CD为曳力系数。

除了相间作用力模型，多相流模型的封闭还需确定水合物颗粒相的黏度μs，计算式见式（6）［16］：

式中，αl为水相体积分数，%；μm为混合相黏度，可用Roscoe-Brinkman方程［17-18］计算得到（见式（7））。

根据式（6）～（7）即可编制用户定义函数（UDF），并以此计算水合物颗粒相的黏度μs。

湍流模型则采用标准k-ε模型，近壁面采用标准壁面函数进行处理。

1.3 群体平衡模型

根据本工作假设，不考虑水合物颗粒的生成分解及水合物颗粒的管壁黏附且认为水合物颗粒粒径连续分布，因此可采用式（8）所示的群体平衡方程［19］：

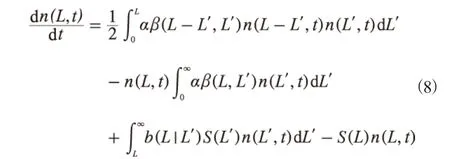
式中，n（L，t）表示粒径为L的水合物颗粒在t时刻的数量密度，m-3；β（L-L′，L′）表示粒径分别为L-L′和L′的水合物颗粒的碰撞频率，m3/s；a为两水合物颗粒发生碰撞后的聚并效率；S（L′）表示粒径为L′的水合物颗粒的破碎频率，s-1；b（L|L′）则表示粒径为L′的水合物颗粒破碎后产生粒径为L水合物颗粒的概率。

基于水合物颗粒聚集动力学，对式（8）中关键参数的计算公式进行选取。

碰撞频率方面，主要考虑由差速沉降和流动剪切造成的碰撞并取两碰撞频率之和作为水合物颗粒的实际碰撞频率。其中，差速沉降碰撞频率（βDS）采用式（9）［20］计算：

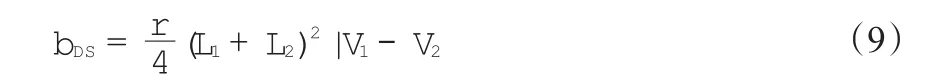
式中，V为沉降速率，m/s，可由式（10）计算得到。

流动剪切碰撞频率方面，当水合物颗粒小于Kolmogorov尺度时，处于湍流耗散区，在这一区域内水合物的聚集行为主要受涡内局部剪切力的影响。此时，水合物颗粒的碰撞频率可用式（11）［21］进行计算；当水合物颗粒大于Kolmogorov尺度时，处于湍流惯性区，在这一区域内水合物被主流场牵引运动。此时，水合物颗粒的碰撞频率可用式（12）［22］进行计算：

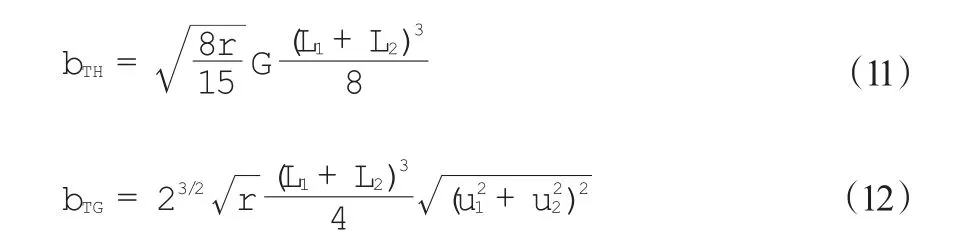
式中，G为流场局部的绝对速度梯度，s-1；u为水合物颗粒的平均速度，m/s。

采用曲线模型计算水合物颗粒间的聚并效率，由于连续相为水，水合物颗粒间不存在液桥力，故计算聚并效率时主要考虑范德华力与流动剪切力之比。聚并效率的计算式见式（13）［23］：

式中，H为表征范德华力大小的哈梅克常数，J；R为发生碰撞两水合物颗粒的调和半径，m。

计算破碎频率时则主要考虑由流动剪切导致的破碎，计算式见式（14）：

式中，E和m为经验常数。

破碎后子颗粒粒径的分布函数方面，本工作采用二元分布作为水合物颗粒破碎后的粒径分布函数［24-25］，表达式见式（15）。

根据式（9）～（15）编制UDF并以此计算群体平衡模型中的关键参数。

1.4 模型求解

利用Fluent 14.5软件，对固液两相流模型和群体平衡模型进行联合求解。管道入口边界条件设定为速度入口，管道出口边界条件设定为压力出口，以二阶迎风差分格式离散动量方程，压力-速度耦合使用SIMPLE算法，群体平衡方程则使用离散法进行求解，瞬态模拟时间步长设置为0.1 s，残差设置为10-5。

模型求解时所涉及的部分参数见表1。

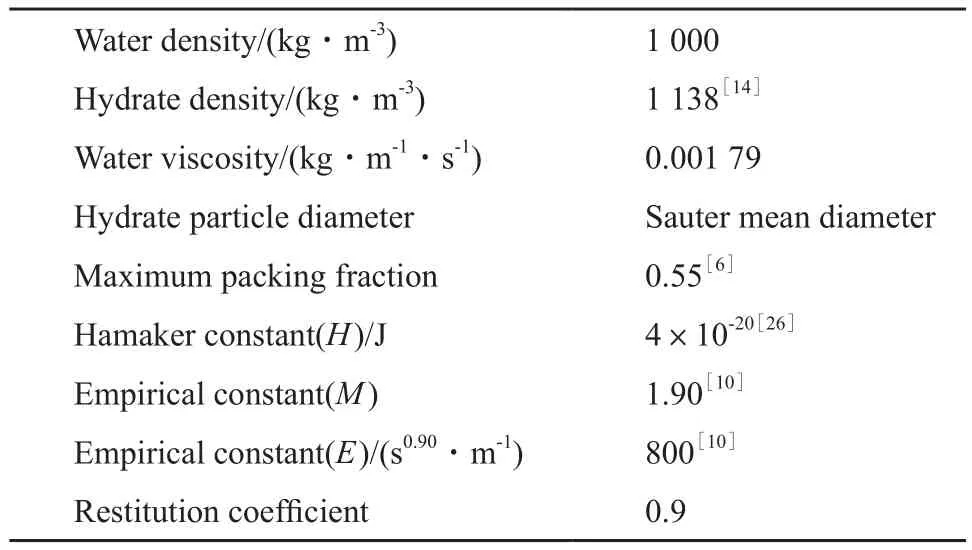
表1 模型参数Table 1 Model parameter

2 结果与讨论

2.1 模拟工况

本工作主要研究流速、水合物颗粒粒径及水合物体积分数对管内水合物颗粒沉积特性的影响，具体模拟工况见表2。

表2 模拟工况Table 2 Simulation condition

2.2 实验验证

流动压降是表征管道内固液两相流流动行为和流动特性的重要参数。根据相关实验［14］，本工作选取流动压降数据对数值模拟结果的可行性和有效性进行实验验证。表3为单位管长压降实验值和模型模拟值的对比。由表3可知，两者的变化趋势相同且两者间的相对误差均小于18%。因此，本工作采用的数值模型和模拟方法能较好地模拟水合物颗粒在管道内的流动行为和流动特性。

表3 实验和模拟条件下单位管长压降对比Table 3 Comparison of pressure gradient between experimental and simulation results

2.3 流速对沉积特性的影响

水合物颗粒的着床沉积主要取决于颗粒所受的惯性力、浮力和重力，对于模拟工况下的水合物，它的密度大于水，故当重力大于浮力和曳力时，水合物颗粒就会沉积，形成床层。由表1可知，本工作中水合物颗粒的最大填充率为0.55，即当管道内水合物体积分数达到55%时，水合物就会沉积形成床层。工况1～5的模拟结果见表4。从表4可看出，当管内水合物初始粒径为5 mm、水合物体积分数为10%时，只有流速为0.05 m/s的工况1发生了水合物沉积，管内局部水合物最高体积分数达到了55%。图3为工况1管道纵截面水合物体积分数云图。由图3可知，水合物沉积主要发生在模拟管段的中后部，在距离模拟管段入口约2.7 m的地方沉积现象最为明显。

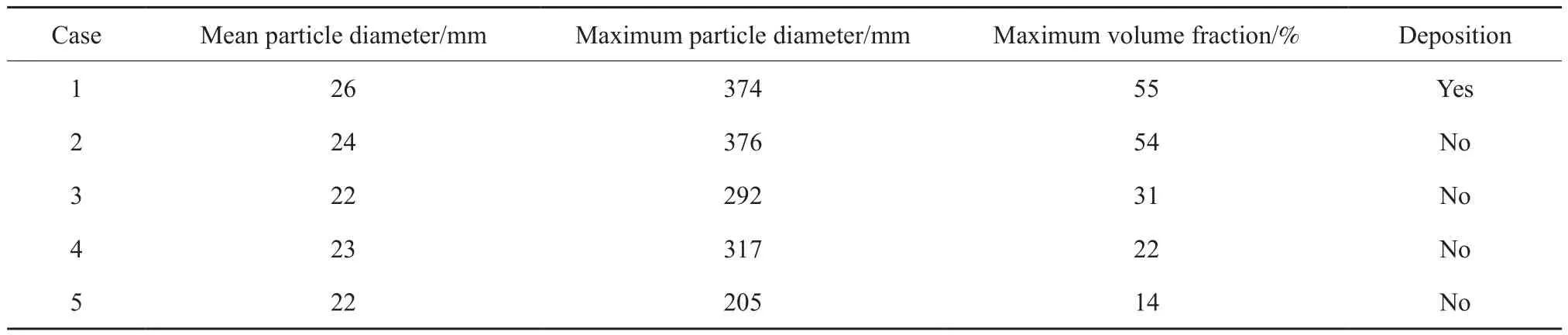
表4 工况1～5的模拟结果Table 4 Simulation results of case 1-5

图3 工况1管道纵截面水合物体积分数云图Fig.3 Contour of hydrate volume fraction distribution in pipeline longitudinal section of case 1.

从表4还可发现，流速的增加对管内水合物颗粒粒径大小的影响不具有明显的规律性，这可能是因为：一方面，由水合物颗粒聚集动力学可知，流动剪切是导致水合物颗粒发生碰撞并产生聚集的主要原因，因此流速越高，水合物颗粒就越容易发生碰撞聚集从而导致粒径增大；另一方面，流动剪切同样是导致水合物颗粒发生剪切破碎的主要原因，因此流速越高，水合物颗粒也越容易发生剪切破碎从而导致粒径减小。流速对管道横截面水合物沉积情况的影响见图4。从图4可看出，流速还会对管内水合物分布产生影响，流速越高，水合物分布就越均匀，水合物颗粒间发生碰撞聚集从而导致粒径增大的概率也就越低。综上所述，模拟工况的低流速范围内，流速的增加对管内水合物颗粒粒径大小的影响并无明显的规律性。

由图4还可看出，在工况1～5距管道入口2.7 m处的管道横截面上，水合物均呈不均匀分布的特征，其中管道下部水合物浓度较高，管道中部水合物浓度分布相对均匀，管道上部水合物浓度则相对较低。固液流型方面，工况1出现了水合物沉积，为固定床层流，工况2～5则为不均匀悬浮流。随着流速的增大，管道下部水合物浓度逐渐降低，管内固液流型从固定床层流（有沉积）逐渐转变为不均匀悬浮流（无沉积），整个管道横截面上水合物的浓度梯度也逐渐减小，水合物分布渐趋均匀。这是因为在管内水合物体积分数和颗粒粒径大小相近的情况下，流速越高，流体对水合物颗粒的携带和分散能力就越强，因此水合物颗粒发生着床沉积的可能性也就越小。

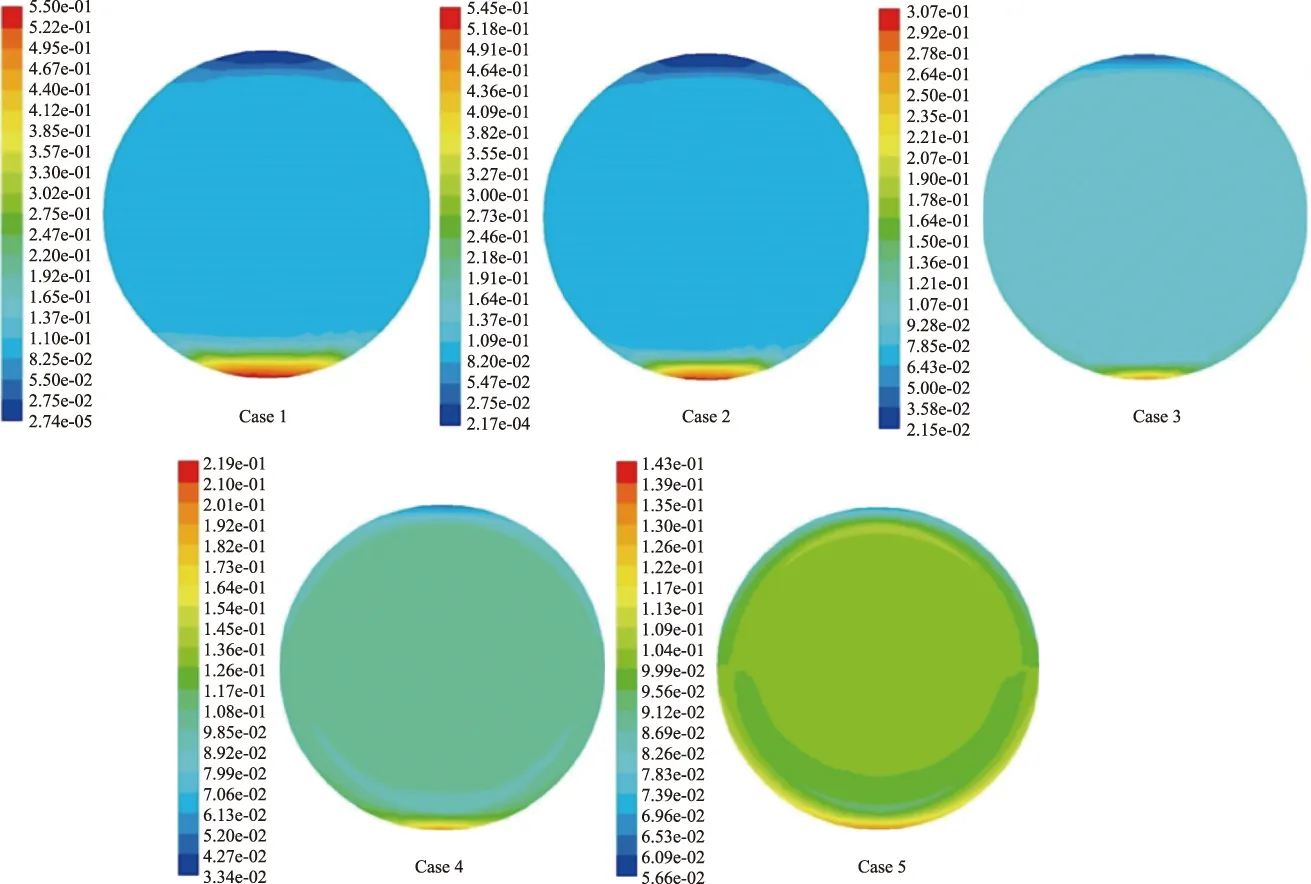
图4 流速对管道横截面水合物沉积情况的影响Fig.4 Influence of flow rate on hydrate deposition in pipeline cross section.

工况1距管道入口2.7 m处管道横截面水合物颗粒粒径分布云图见图5。

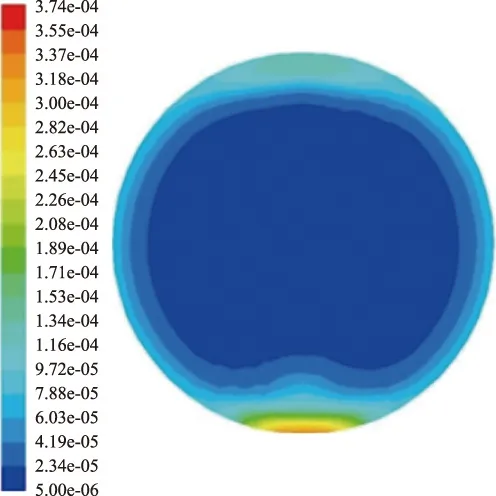
图5 工况1管道横截面水合物颗粒粒径分布云图Fig.5 Counter of hydrate particle diameter distribution in pipeline cross section of case 1.

由图5可知，发生沉积时，管道横截面处的水合物颗粒粒径分布与水合物分布保持了较好的一致性。管道下部水合物颗粒粒径较大，管道上部水合物颗粒粒径较小，管道中部水合物颗粒粒径分布则较均匀。这除了因为大粒径水合物颗粒更易发生着床沉积外，还与管道下部水合物浓度高，水合物颗粒更易发生碰撞聚集从而导致粒径增大有关。

图6为工况1模拟管道各部分的水合物颗粒粒径分布直方图。由图6a可知，模拟开始时，管道内的水合物颗粒大小均在35 μm以下。之后，随着水合物颗粒在流动过程中不断聚集和破碎，管道内水合物颗粒的粒径逐渐变化到5～350 μm之间，近似呈对数正态分布（见图6b）。最后，由于流速较低，颗粒粒径大于70 μm的水合物颗粒几乎全部发生着床沉积，只有粒径小于70 μm的水合物颗粒在管道出口流出（见图6c）。

图6 工况1水合物颗粒粒径分布直方图Fig.6 Hydrate particle size distribution histogram of case 1.

2.4 水合物颗粒粒径对沉积特性的影响

工况1及工况6～9的模拟结果见表5，水合物颗粒初始粒径对水合物起始沉积位置的影响见图7。从表5可看出，当管内水合物体积分数为10%、管道入口流速为0.05 m/s时，水合物初始粒径在5～200 μm之间的5组工况全部发生了水合物着床沉积。从图7可看出，不同于工况1的是，工况6～9中水合物颗粒的起始沉积位置均距离管道入口较近，且水合物颗粒的初始粒径越大，水合物颗粒的起始沉积位置距管道入口越近。此外，从表5还可看出，随着模拟时水合物颗粒初始粒径的增大，模拟得到的水合物颗粒平均粒径和最大粒径也逐渐增大。

表5 工况1及工况6～9的模拟结果表Table 5 Simulation results of case 1 and case 6-9

图7 水合物颗粒初始粒径对水合物起始沉积位置的影响Fig.7 Influence of initial hydrate particle diameter on initial hydrate deposition position.

图8为工况1及工况6～9距管道入口2.7 m处管道横截面水合物体积分数云图。由图8可知，由于出现水合物颗粒的着床沉积，上述5组工况对应的固液流型均为固定床层流。其中，管道下部水合物浓度较高形成固定床，中部水合物浓度分布相对均匀，上部水合物浓度则相对较低，几乎无水合物颗粒存在（体积分数均低于0.004%）。由表5可知，随着水合物颗粒初始粒径的增大，模拟过程中管内水合物颗粒的平均粒径及最大粒径也逐渐增大，因此管内水合物的沉积情况渐趋严重，具体表现为管道下部高浓度水合物区和管道上部低浓度水合物区的范围逐渐增大，管道横截面上水合物的浓度梯度也越来越大。因此，在其他条件相同时，管内水合物颗粒粒径越大，管道横截面处水合物分布越不均匀，管内水合物沉积现象也越明显。

值得注意的是，由图8可看出，从工况1到工况6～9，管道横截面处水合物沉积层的高度并未出现明显变化。这是因为，工况1和工况6～9的床层高度为距管道入口2.7 m的管道横截面处的床层高度。而由图7及前文分析可知，不同工况下水合物在管道内的起始沉积位置不同，同一工况下不同管道长度处水合物沉积层高度也不相同。因此，距管道入口2.7 m的管道横截面并不是所有工况下水合物在管道内沉积层高度最大的位置，故图8中各个工况的床层高度并不能反映各个工况下管道内水合物沉积的严重程度。不同工况下管道内水合物沉积的严重程度应当从管道内水合物沉积层的长度和沿程高度（即水合物沉积总量）来判断，而不能单独从某一截面上水合物沉积层的高度进行准确判断。综上所述，即使从工况1到工况6～9，管内水合物的沉积情况越来越严重，但在管道某一长度的横截面处（比如距入口2.7 m处），各工况的水合物沉积层高度仍可能相差不大。

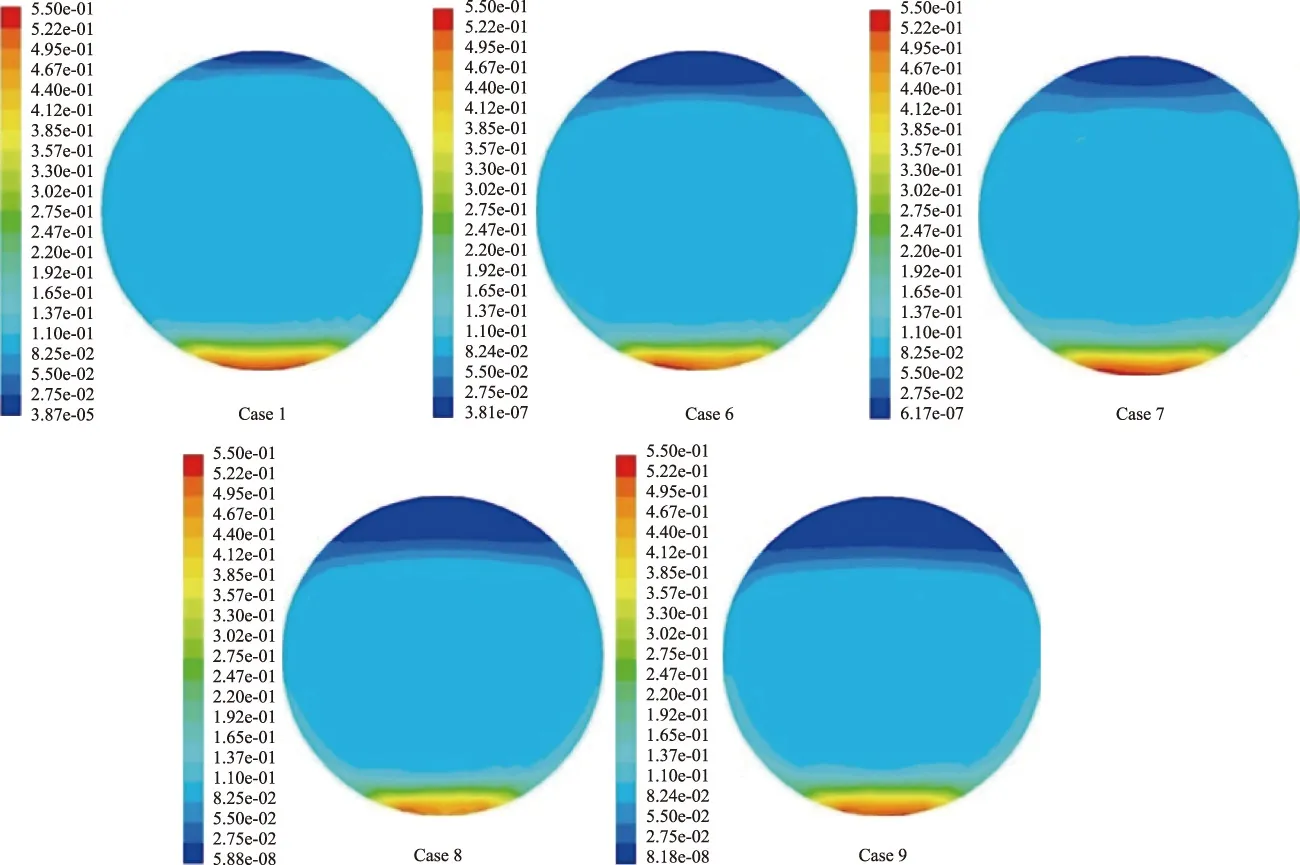
图8 颗粒粒径对管道横截面水合物沉积情况的影响Fig.8 Influence of hydrate particle diameter on hydrate deposition in pipeline cross section.

2.5 水合物体积分数对沉积特性的影响

工况1及工况10～13的模拟结果见表6。从表6可看出，当管内水合物颗粒初始粒径为5 μm、管道入口流速为0.05 m/s时，水合物体积分数在10%～50%之间的5组工况全部发生了水合物着床沉积。同工况6～9类似，工况10～13中水合物颗粒的起始沉积位置均距离管道入口较近，且水合物体积分数越大，水合物颗粒的起始沉积位置距管道入口越近。从表6还可看出，随着模拟时水合物体积分数的增大，模拟得到的水合物颗粒的平均粒径和最大粒径也逐渐增大。

表6 工况1及工况10～13的模拟结果Table 6 Simulation results of case 1 and case 10-13

图9为工况1及工况10～13距管道入口2.7 m处管道横截面水合物体积分数云图。由图9可知，由于出现水合物颗粒的着床沉积，上述5组工况对应的固液流型均为固定床层流。其中，管道下部水合物浓度较高并形成固定床，管道中部水合物浓度分布相对均匀，管道上部水合物浓度则相对较低。

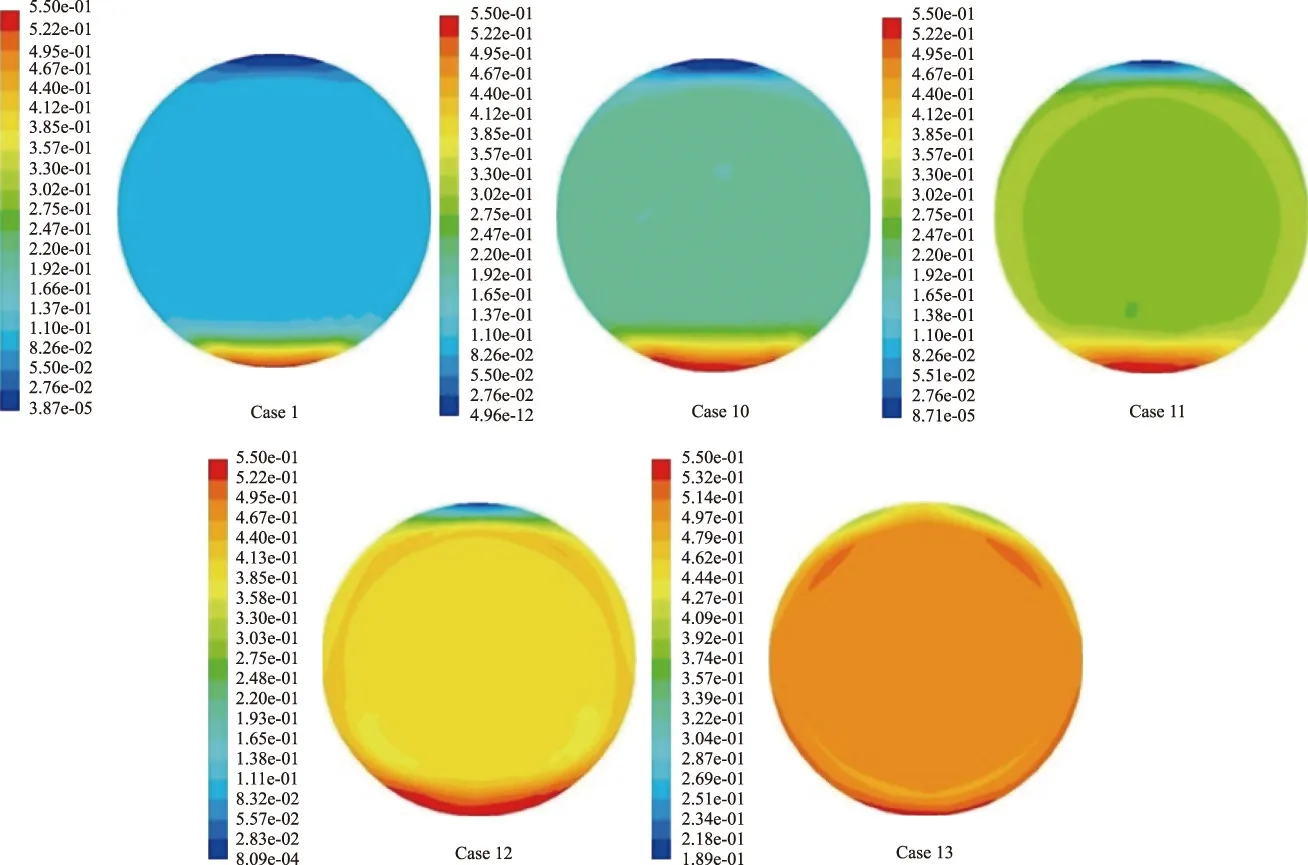
图9 水合物体积分数对管道横截面水合物沉积情况的影响Fig.9 Influence of hydrate volume fraction on hydrate deposition in pipeline cross section.

表7为工况1及工况10～13的管内水合物分布。如表7和图9所示，随着管内水合物体积分数的增大，管内高水合物浓度（50%～55%）区所占的比例逐渐增大。因此，在其他条件相同时，管内水合物体积分数越大，水合物沉积现象越明显。

表7 工况1及工况10～13的管内水合物分布Table 7 Hydrate volume fraction distribution of case 1 and case 10-13

3 结论

1）引入基于水合物颗粒聚集动力学的群体平衡模型，并将该模型与固液两相流模型相结合，通过Fluent软件进行联合求解可实现对管道内水合物颗粒沉积特性的精确模拟。

2）着床沉积发生时，管道横截面处的水合物分布和粒径分布有较好的一致性。其中，管道下部水合物浓度高、粒径大，管道上部水合物浓度低、粒径小，管道中部水合物的浓度和粒径分布则较为均匀。

3）流速的增大会减小管道横截面上水合物的浓度梯度，使水合物分布渐趋均匀，从而减弱水合物的着床沉积。

4）管内水合物颗粒的初始粒径越大、体积分数越高，水合物颗粒平均粒径和最大粒径的模拟值越大，水合物颗粒的起始沉积位置距管道入口越近，管内水合物的沉积情况越严重。

符 号 说 明

a 聚并效率

b 子颗粒粒径分布函数

CD曳力系数

E 经验常数

G 绝对速度梯度，s-1

g 重力加速度，m/s2

H 哈梅克常数，J

kls动量传递系数，

L，L′ 水合物颗粒粒径，m

M 相间动量交换，kg/（m·s）2

m 经验常数

n 数量密度，m-3

p 压力，Pa

R 调和半径，m

S 破碎频率，s-1

t 时间，s

u 速度矢量，m/s

u 平均速度，m/s

ur相间相对流速，m/s

V 沉降速率，m/s

α 体积分数

β 碰撞频率，m3/s

ρ 密度，kg/m3

σdPlanck 扩散系数

τ 应力张量

μ 动力黏度，Pa·s

下标

1，2 分别表示不同的水合物颗粒

DS 差速沉降

di 相间拖曳力

i 水相或水合物相

l 水相

m 混合相

ST 层流剪切

s 水合物相

TH 湍流耗散区

TG 湍流惯性区

t 湍流

ti 湍流扩散力

［1］ Sloan E D. Natural gas hydrates in fl ow assurance［M］.New York：Elsevier Science Ltd，2010：1-36.

［2］ Song Guangchun，Li Yuxing，Wang Wuchang，et al. Experimental study of hydrate dissociation in oil-dominated systems using a high-pressure visual cell［J］.J Nat Gas Sci Eng，2017，45：26-37.

［3］ 宋光春，李玉星，王武昌，等. 油气输送管线水合物沉积研究进展［J］.化工进展，2017，36（9）：3164-3176.

［4］ Song Guangchun，Li Yuxing，Wang Wuchang，et al. Investigation of hydrate plugging in natural gas+diesel oil+water systems using a high-pressure fl ow loop［J］.Chem Eng Sci，2017，158：480-489.

［5］ Jassim E，Abdi M A，Muzychka Y. A new approach to investigate hydrate deposition in gas-dominated fl owlines［J］.J Nat Gas Sci Eng，2010，2（4）：163-177.

［6］ 魏丁，王武昌，李玉星，等. 管道 CCl3F 水合物浆流动特性的数值模拟［J］.油气储运，2016，35（8）：828-832.

［7］ 陈鹏，刘福旺，李玉星，等. 水合物浆液流动特性数值模拟［J］.油气储运，2014，33（2）：160-164.

［8］ 刘海红. 水合物颗粒受力及聚结特性研究［D］.青岛：中国石油大学（华东），2014.

［9］ 李莹玉. 天然气水合物颗粒在流场中的聚集行为研究［D］.天津：中国民航大学，2013.

［10］ 王晓娅. 管输水合物浆液流动特性研究［D］.天津：中国民航大学，2015.

［11］ Fatnes E D. Numerical simulations of the flow and plugging behavior of hydrate particles［D］.Bergen：University of Bergen，2010.

［12］ Camargo R，Palermo T. Rheological properties of hydrate suspensions in an asphaltenic crude oil［C］//International Conference on Gas Hydrates，Yokohama：ICGH4，2002.

［13］ Balakin B V，Lo S，Kosinski P，et al. Modelling agglomeration and deposition of gas hydrates in industrial pipelines with combined CFD-PBM technique［J］.Chem Eng Sci，2016，153：45-57.

［14］ Balakin B V，Pedersen H，Kilinc Z，et al. Turbulent fl ow of freon R11 hydrate slurry［J］.J Pet Sci Eng，2010，70（3/4）：177-182.

［15］ Ding Jianmin，Gidaspow D. A bubbling fluidization model using kinetic theory of granular fl ow［J］.AIChE J，1990，36（4）：523-538.

［16］ 王继红. 冰浆的管道输送热流动特性［D］.大连：大连理工大学，2013.

［17］ Pabst W. Fundamental considerations on suspension rheology［J］.P R Soc A，2004，48（1）：6-13.

［18］ 赵鹏飞，王武昌，李玉星，等. 管道内水合物浆流动的数值模型［J］.油气储运，2016，35（3）：272-277.

［19］ Hulburt H M，Katz S. Some problems in particle technology：A statistical mechanical formulation［J］.Chem Eng Sci，1964，19（8）：555-574.

［20］ Camp T R，Stein P C. Velocity gradients and internal work in fl uid motion［J］.J Bsn Soc Civ Eng，1943，30（4）：219-237.

［21］ Saffman P G，Turner J S. On the collision of drops in turbulent clouds［J］.J Fluid Mech，1956，1：16-30.

［22］ Abrahamson J. Collision rates of small particles in a vigorously turbulent fluid［J］.Chem Eng Sci，1975，30（11）：1371-1379.

［23］ van de Ven T G M，Mason S G. The microrheology of colloidal dispersions Ⅶ. Orthokinetic doublet formation of spheres［J］.Colloid Polym Sci，1977，255（5）：468-479.

［24］ Zhang Jianjun，Li Xiaoyan. Modeling particle-size distribution dynamics in a fl occulation system［J］.AIChE J，2003，49（7）：1870-1882.

［25］ 李振亮. 基于群体平衡的活性污泥絮凝动力学［D］.重庆：重庆大学，2014.

［26］ Li Xiaoyan，Logan B E. Collision frequencies between fractal aggregates and small particles in a turbulently sheared fluid［J］.Environ Sci Technol，1997，31（4）：1237-1242.