FDM-3D打印机的精度治理与误差补偿研究

王 凯，李必文，胡良斌，王林超

（南华大学机械工程学院，湖南 衡阳421001）

0　引言

基于熔融沉积快速成形技术（FDM）的3D打印机是目前普及率最高的3D打印机之一，具有软件开源、成本低廉、易于推广应用的优势[1-2]。如何提高其成形几何精度特别是桌面级3D打印机以彰显其性价比优势并拓展其应用范围，是生产厂家及用户普遍关心的问题。与其它类型的3D打印机一样，FDM-3D打印机也不可避免地存在原理性误差、数据处理误差以及加工误差[3-4]。原理性误差是指模型切片时的误差，一般根据成形件的形状和尺寸设置层厚来控制；数据处理误差是指三维数据转化成STL文件时的误差，一般根据处理设备的运算能力和模型精度要求对参数进行优选；加工误差主要影响因素是机床的几何误差[5]，逐项分析各几何误差源，很多是可检测、可调整的，即是可治理的。在误差治理的基础上，采用优化的工艺参数进行打印试验及误差检测，可建立误差预测模型并进行误差补偿。本文提供了误差预测模型和补偿技术的研究方法，为后续试验验证提供了理论支撑，是提高此类3D打印成形几何精度的有效途径。

1　影响加工精度的误差来源

FDM-3D打印机机床加工精度的主要影响因素是机床的几何误差，分为：（1）静态几何误差，即加工原理误差、机床结构件的制造误差、装配误差以及数控误差；（2）动态几何误差，即工艺系统的受力变形、热变形、振动等引起的误差。上述误差各自独立影响加工精度可按概率法合成：

式中：△z为3D打印机加工误差极限值；△i为各误差因素极限值。

根据FDM-3D打印是通过动平台带喷嘴移动，在静平台上逐层对任意轮廓的单层面体进行成形加工的原理，而且应用时一般采用优化的工艺参数进行打印试验，检测调整机床Z方向上的几何误差。并且由于层厚设置值很小，调整后的机床Z方向上的几何误差不影响单层面体的加工精度。基于此，本文只需研究加工任一单层面体时FDM-3D打印机机床几何误差对加工精度的影响。

2　精度治理与单层面体轮廓几何误差预测

2.1　原始几何误差分类

轮廓上各加工点的几何误差影响单层面体的3D打印精度，是所有各误差因素共同作用的结果。根据FDM-3D打印的特点，对表1所列各原始几何误差项目对单层面体轮廓加工精度的影响进行分析，以提炼出检测治理项目。

表1　原始几何误差项

对表1中各原始几何误差分析如下：

（1）G1、G2、G4、G7四项原始几何误差对单层面体轮廓加工精度无影响或可从略，但 G1、G2、G4、G7仍然会影响零件成形精度。其中：G1可通过检测调整使初始成形面达到要求；G2、G4需要厂家保证对应部件的制造精度以及机床的安装精度来控制；G7由FDM-3D打印机机床数控系统的输出稳定性确定，可根据加工精度要求选配。

（2）G3、G5、G6、G8四项原始几何误差直接影响 3D打印机机床对单层面体轮廓加工精度，可在精度治理的基础上采用方差合成原理合成各误差项，需要实验检测FDM-3D打印机机床运动中误差的实际值。其中：G3、G5对单层面体轮廓几何误差的影响与加工尺寸成正比关系，但影响方向不确定属于未定系统误差；G6、G8对单层面体轮廓几何误差的影响与加工尺寸无明显关系，属于随机误差。

2.2　几何误差的治理

结合FDM-3D打印机机床加工特点，治理初始成形面的平面度能有效地提高3D打印机的加工精度。方法如下：

（1）检测调整G1，将该型打印机置于铸铁检测平台上，用磁力表座固定杠杆百分表使其测头接触3D打印机静平台并调零；沿一定的路径移动表座，记录杠杆百分表读数，计算读数的最大差值即为平面度误差；分析平面度误差值出现静平台上的区域，用塞尺垫起静平台使其平面度满足成形要求。如图1所示为某型3D打印机平面度检测调整。

图1　平面度检测调整

（2）以调整后的静平台为基准平面，利用Pronterface软件（如图2所示）控制3D打印机，使其动平台上装有百分表的测量头移动到打印范围最远端且缓慢贴进静平台面位置点，分别调节各位置的调平螺丝使读数一致。

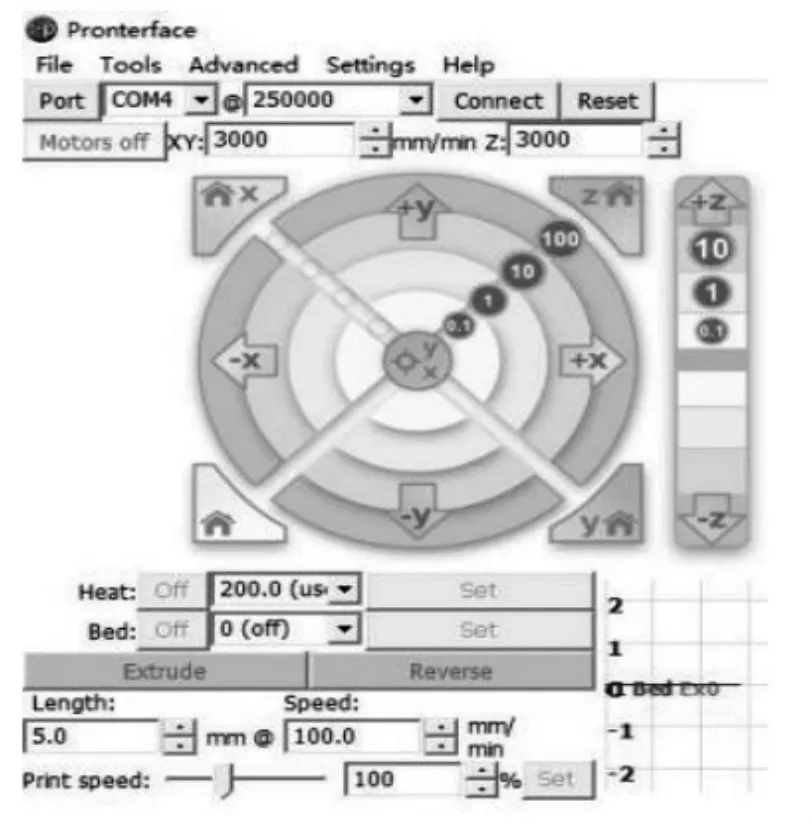
图2　Pronterface软件界面

2.3　单层面体轮廓几何误差的预测

根据误差理论[6]不同性质的误差按极限误差合成，由式（1）可以得到3D打印机机床几何误差在X、Y方向上的误差预测极限值△x、△y：

式中，△Gx6、△Gy6为动平台移动分别在X、Y方向上的测量结果，相当于失动量引起的坐标误差极限值；△Gx8、△Gy8为在X、Y方向上单指令进给误差极限值；△Gx3、△Gy3分别为在X、Y方向L长度上测得的直线度误差值；△G5为测得的在X方向L长度上X轴对Y轴的垂直度误差值。

3　基于预测方式的误差修正技术

图3　任意曲线段的直线拟合

3.1　建立修正值的优化模型

如图4所示，当加工多段线轮廓到第i个点的位置时，为了保证第i个点到第i+1个点之间的线段的加工精度，需要实际加工直线段（虚线表示）尽可能接近理论上加工直线段（实线表示）。对加工多段直线人为设误的补偿技术可以认为是旋转和平移实际加工轮廓直线段，使之与理论多段线的匹配效果按最小二乘原则达到最佳[7]，即寻找出实际加工直线段向理论上加工直线段匹配过程中在X、Y方向的平移量 a、b 和旋转角度 λ 的最优值。设是匹配过程中实际多段线上顶点（Xi，Yi）经平移旋转后的坐标：

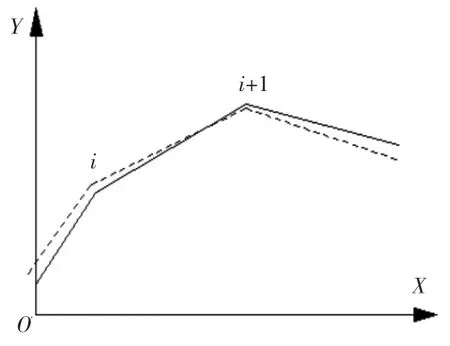
图4　部分折线段误差

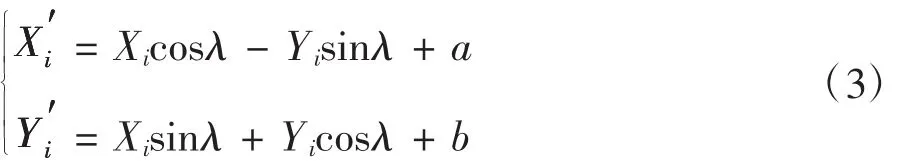
设（xi，yi）为理论多段线上顶点坐标。根据最小二乘原则，用多段线轮廓上所有点偏差平方和最小构造匹配过程中的目标函数，得：

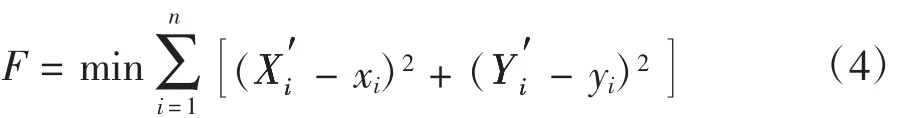
由 θ＝ arctan（y/x）可以推得△θ与△x、△y的误差传递关系，则任一直线段的角度误差预测极限值为：

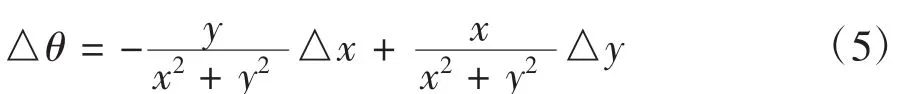
式中△x、△y按式（2）计算。则约束条件为：

利用MATLAB最优化工具箱进行求解，即可得到在X、Y方向的平移量a、b和旋转角度λ预先修正的设置最优值。

3.2　曲线轮廓的重生成

将平移量a、b和旋转角度λ的最优解代入式（3），即能得到在XOY平面内的n组坐标值，这些坐标值就是单面体轮廓型值点的坐标值。以折线拟合的方法形成轮廓线，其连续性、保形性及拟合误差可有效控制。但要保证轮廓曲线的光滑性，则型值点必须足够多、足够密，这就必然给数学处理带来很大的工作量。如果以样条线拟合型值点，其连续性、光滑性能得到保证，但保形性和插值点的拟合误差难以有效控制。实际工作中经常用到TableCurve-2D软件对轮廓曲线进行分段拟合[8]，通过综合控制剩余标准误差σ与相关指数R2，在保证拟合精度的前提下，同时保证拟合曲线的连续性、光滑性和保形性。

4　结束语

本文分析了FDM-3D打印单层面体轮廓加工误差的来源，在进行有效精度治理以及相关几何误差检测的基础上，提供了一种误差预测模型和修正技术，对后续提升FDM-3D打印单层面体加工的几何精度具有理论意义。

参考文献：

[1]Yan Yongnian，LI Shengjie，Zhang Renji et al.Rapid Prototyping and Manufacturing Technology： Principle， Representative Technics，Applications，and Development Trends[J].Ts-inghua Science&Technology，2009，14（S1）：1-12.

[2]Rhys Jones，Patrick Haufe，Edward Sells，Pejman Iravani，Vik Olliver，Chris Palmer，Adrian Bowyer.RepRap-the replicating rapid prototyper[J].Robotica，2011，29（1）：20-25.

[3]杨恩源．基于FDM快速成型工艺的优化[J]．北京服装学院学报，2012，32（1）：70－72．

[4]朱 静，伍冯洁，韩晓英，等.浅谈FDM打印机的误差分析与3D模型质量优化[J].东莞理工学院学报，2015，22（5）：99-103.

[5]朱 家，蔡 立.电加工机床加工误差实用分析法及其应用[J].电工，1992（04）：40-46.

[6]费业泰．误差理论与数据处理[M]．北京：机械工业出版社，2010：57-70.

[7]黄东兆，周会成，李 斌，等.面向轮廓精度控制的误差补偿方法[J].华中科技大学学报（自然科学版），2008（02）：13-16.

[8]李必文.机械设计分析中的曲线拟合[J].现代制造工程，2008（05）：24，72-74.