数字波束成形中峰均比抑制方法的研究

刘璐，赵国庆



数字波束成形中峰均比抑制方法的研究

刘璐1,2，赵国庆1

（1. 西安电子科技大学电子工程学院，陕西 西安 710071；2. 西安邮电大学通信与信息工程学院，陕西 西安 710121）

数字波束成形技术是5G通信中的关键技术之一。然而，数字波束成形中过高的峰均比会造成信号发射端功率放大器进入非线性工作区域。针对现阶段概率类方法中的选择性映射类算法带宽利用率低和运算复杂度高的问题，提出一种基于MUSIC算法的盲选择性映射方法。该方法不用传输边带信息，就可提高频带的利用率；同时，在运算复杂度和峰均比的抑制效果上，所提方法较选择性映射算法有一定的改善。

数字波束成形；峰均比抑制；选择性映射算法；MUSIC算法

1 引言

数字波束成形（DBF, digital beam-forming）技术可以增强特定方向的信号，在干扰方向形成零陷，因而被广泛地应用在5G通信中。但随着阵列天线阵元数的增加，波束成形过程中会伴随着过高的峰均比（PAPR, peak-to-average power ratio）。而过高的峰均比会导致发射端的高功率放大器工作在饱和区域，将会造成发射信号的畸变，同时会产生严重的带内干扰以及带外噪声。现阶段，针对峰均比抑制这一问题，有很多的解决方案被提出[1~6]。在这些方案中，由于选择性映射（SLM, selected mapping）算法不会造成信号的畸变与失真，因而在研究峰均比抑制的过程中，引起人们的广泛关注。然而，SLM方法在信道传输中，需要传输关键的边带信息（SI, side information），这会造成信道带宽利用率降低和接收端解码复杂度增加。

进而，一些关于盲SLM的方法逐渐被提出[7~9]。文献[7,8]中提出了最大似然解码法和简化的最大似然解码法。但是，由于大数据的高复杂度导致最大似然解码法几乎无法在实际中应用。而简化的最大似然解码法的运算复杂度依然很高。文献[9]提出了将SI嵌入传输信号里的方法，应用扩展相位符号的位置来寻找边带信息，但在解码过程中需要逐一对所有的相位序列进行与扩展相位符号的匹配，复杂度也较高。本文提出一种基于MUSIC的盲SLM（MB-SLM, MUSIC based blind-SLM）算法。在该算法中，通过对经过旋转相位因子运算后的最小的那路合成的信号的相关函数进行奇异值分解（SVD, singular value decomposition），标记此时的噪声子空间，记为密钥。而这一路最小的信号与此噪声子空间，也就是密钥正交，最后在信号通过发射端的功率放大器时，经密钥解密出最小的合成波束。由于在该算法中不需要在相位序列中嵌入边带信息，进而不需要在频带内传输SI，因此，带宽利用率较高。同时，本文算法不需要对最大似然函数的搜索解码，也不需要进行相位符号的扩展，因此，运算的复杂度也较低。

2 数字波束成形模型

2.1 现代通信技术中的波束成形

在现代通信中，将无线信号（电磁波）只按特定方向传播的技术叫作数字波束成形。和光束一样，当所有波的传播方向都一致时，即形成了波束图，如图1所示。

图1 通信中的波束成形

无线通信电磁波的信号能量在发射端由天线辐射进入空气，并在接收端由天线接收。因此，电磁波的辐射方向由天线的特性决定。天线的方向特性可以由辐射方向图（即天线发射的信号在空间不同方向的幅度）来描述。普通天线的辐射方向图方向性很弱，由于传统的电磁波具有强的发散性（空间360°），每个方向的辐射强度都基本一样，电磁波在某一特定方向的磁场强度就会变弱。这就需要用波束成形技术来进行能量的合成。而最基本的形成波束的方法则是使用辐射方向性很强的天线，在特定的某一方向上形成强烈场强的电磁波束，如图2所示。

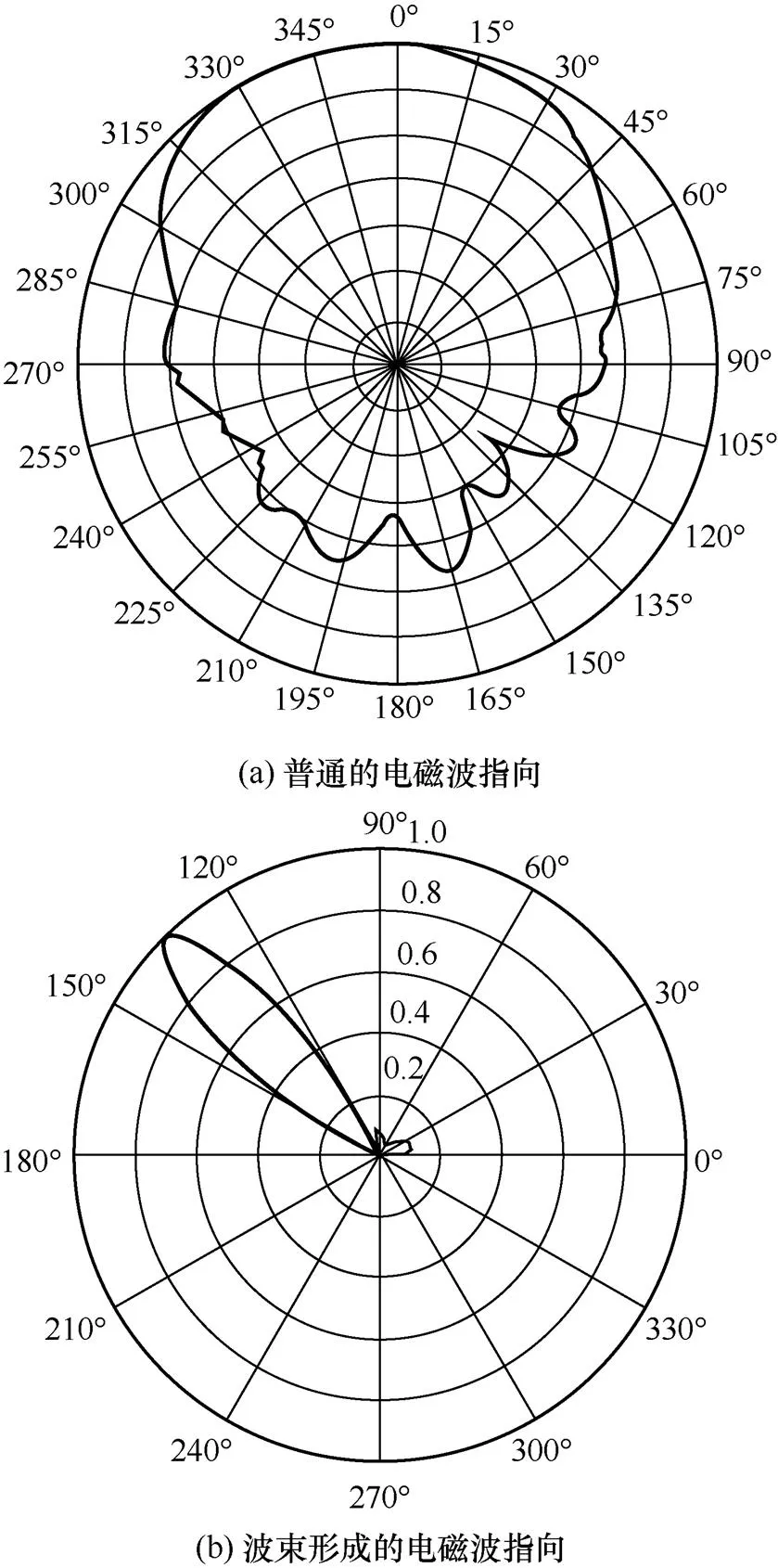
图2 电磁波指向

在波束成形中，各个天线阵列阵元通过仔细控制波源发射与接收的波之间的相对相位和幅度，将电磁波辐射与接收增益都集中在一个目标方向上。同时，其他地方电磁波辐射与接收增益都很小，在干扰方向形成零陷，在目标方向传播的电磁波确定后，对于不同阵元上的电磁波，都加入一个特定的相位时延用来补偿波前到达天线的相位差，从而不同天线阵元合成的波束在经过加权求和后幅度会变大，进而完成波束的合成。

2.2 波束成形的模型

在均匀线阵的阵列天线中，入射平面电磁波到达各相邻天线的波程差相同。各个被补偿的信号经过叠加，接收阵列增益达到最大，此时的电磁波入射方向就是阵列波束成形的方向[10,11]，具体如图3所示。

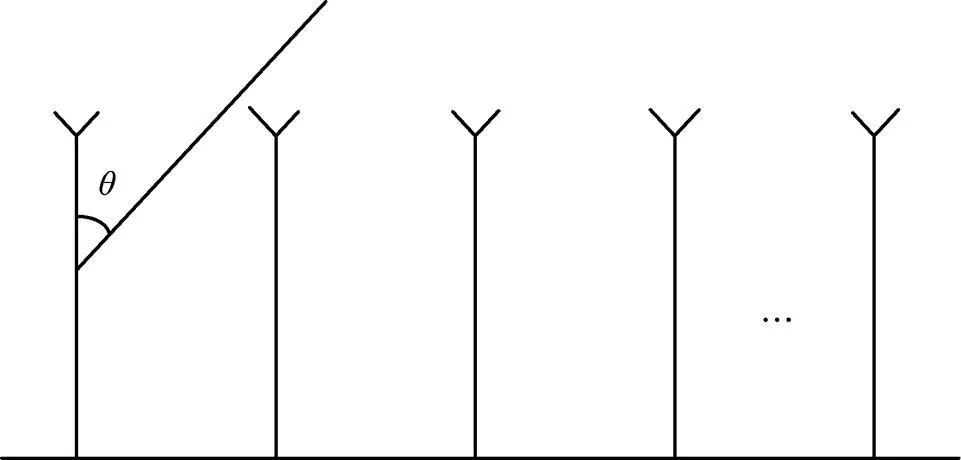
图3 阵列天线的波束成形

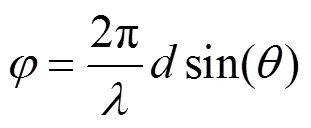
均匀线阵波束成形后阵列的输出为

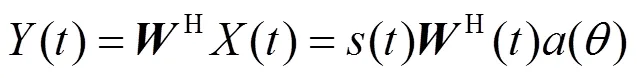
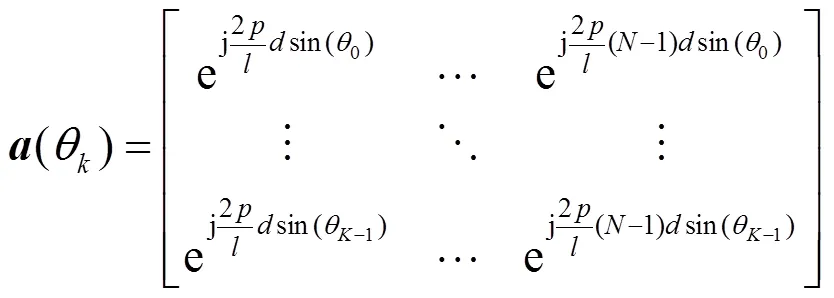
2.3 传统选择性映射算法及峰均比抑制标准

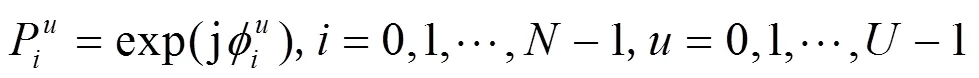
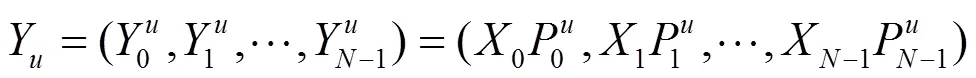
波束成形是由各路阵元的信号通过一定的优化准则加权而成，它的可以被定义为

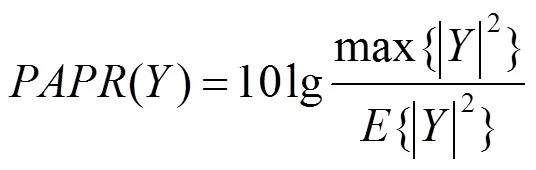
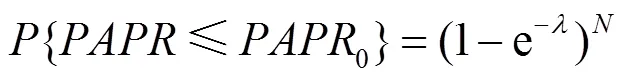
它的互补累积概率分布函数（CCDF, complementary cumulative distribution function）表示的分布，即统计的峰均比超过所限定的峰均比门限的概率，为

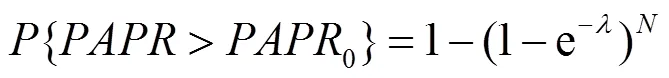
由式(8)可以看出，当天线阵列阵元越多时，越大，大的峰均比出现的概率越大，因而限制大的峰均比越必要。而的最高值一般被称为波峰因子，记为CREST（峰值）。

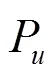
3 MB-SLM算法模型

3.1 MB-SLM的盲边带传输模型

本文提出了一种基于MUSIC算法的盲选择性映射方法。该算法不用传输表示序列号码的边带信息，因而也不需使用附加的信道宽度，提高了信道的利用率，同时在复杂度方面也有优化。

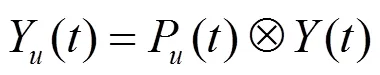
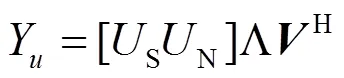
图4 MB-SLM算法的原理框架

3.2 MB-SLM算法的运算复杂度优化模型

3.2.1 MB-SLM和C-SLM算法复杂度的比较

正交矩阵的性质如性质1所示。

性质1 正交矩阵行列式的值为1或−1，即det||=1或det||=−1。

证毕。

由性质1可知，正交矩阵行列式的平方为1。

线性约束最小方差（LCMV，linearly constrained minimum variance）准则要求在某一特定方向上的功率在一定的条件下，调节权矢量，使输出的功率最小，从而达到自适应的目的。最小功率准则实质上就是LCMV优化准则，在波束成形过程中采用的优化约束准则为

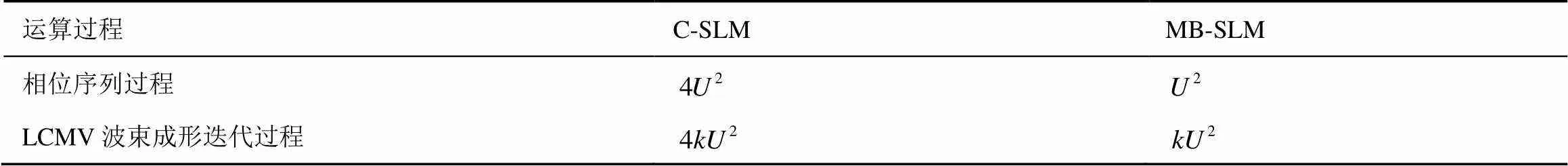
表1 不同算法的复杂度对比

3.2.2 MB-SLM和嵌入SI的SLM算法复杂度的比较

文献[4]提出了嵌入SI的SLM（ESI-SLM, embedded side information SLM）算法。在ESI-SLM算法中，将SI嵌入导频信息中，其中，SI检测的检测优化准则为

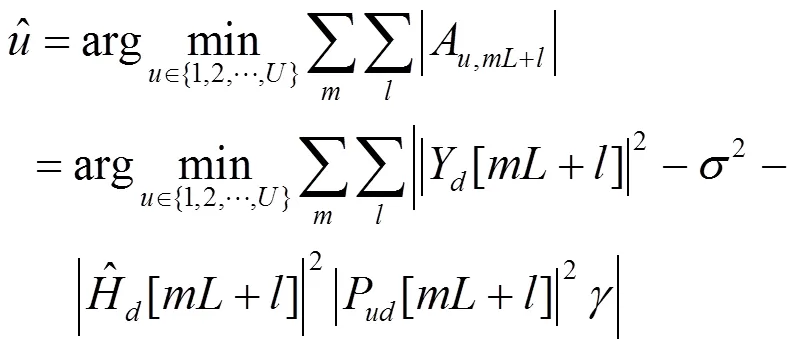
合成波束的检测恢复准则为

(15)

综上所述，MB-SLM算法总结如下。

5) 通过产生的密钥在发送端解密出最小的合成波束。

4 仿真实验及结果分析

4.1 MB-SLM算法的PAPR抑制性能的仿真验证

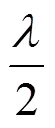
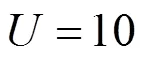
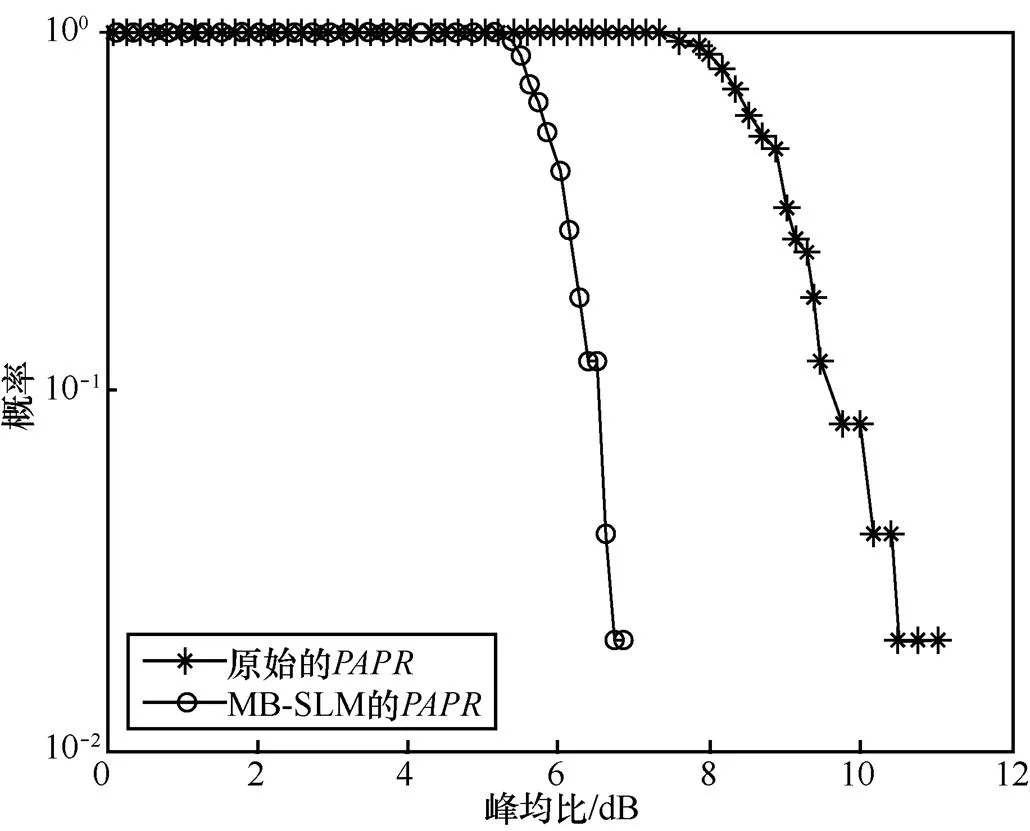
图5 MB-SLM算法与未经过处理的信号峰均比的比较

4.2 蒙特卡洛分析

在波束合成的过程中，经过旋转相位因子产生相位序列与合成波束在相乘的过程中，会出现检测最小相位序列错误的现象，采用蒙特卡洛方法对算法的误码率（BER, bit error rate）进行仿真及验证研究，对比在同一组波束合成数据下的MB-SLM算法、C-SLM算法[14]和ESI-SLM算法[15]的BER。仿真实验的条件设置如下：蒙特卡洛次数200次，波束成形的方向分别为0°、20°、45°。

仿真条件1 波束成形方向为0°，信噪比为−20~10 dB。波束方向为0°时3种算法的BER比较如图6所示。

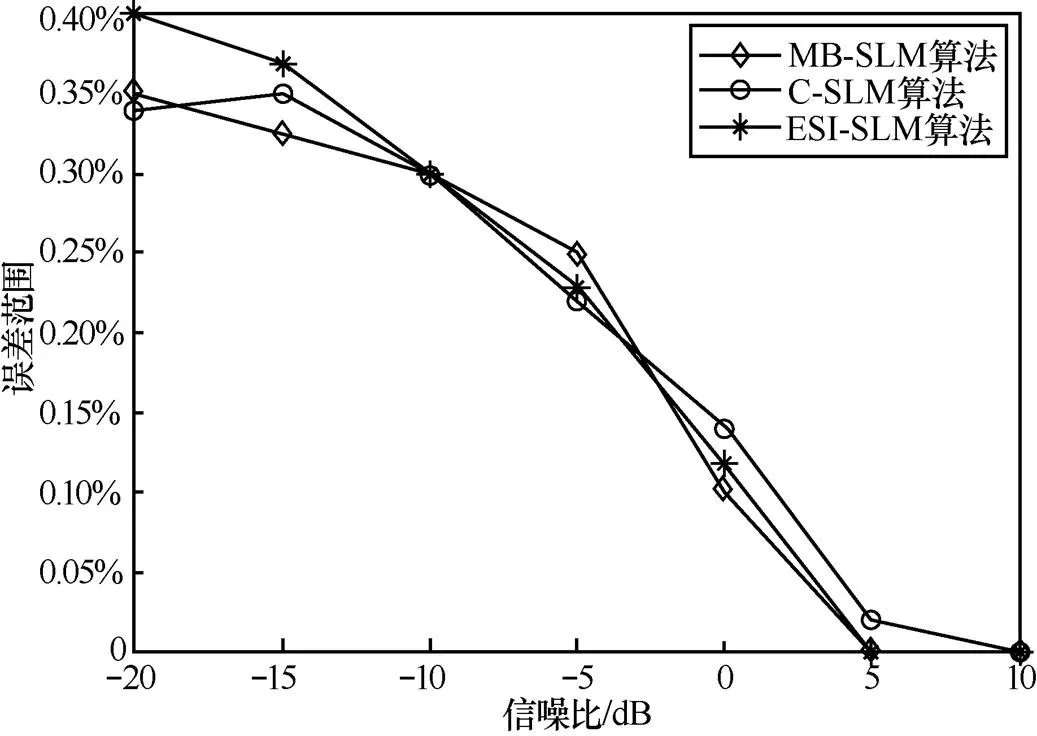
图6 波束方向为0°时3种算法的BER比较

由图6可知，在信噪比环境逐渐变好的情况下，MB-SLM算法的误差范围从0.35%逐渐减小，且与C-SLM算法[14]和ESI-SLM算法[15]的BER基本相同，误差范围基本控制在0.35%以内，误差不是很大。因此，本文算法在一定信噪比范围内对检测出最小相位序列有一定的可行性。

仿真条件2 波束成形方向为20°，信噪比为−20~10 dB。波束方向为20°时3种算法的BER比较如图7所示。

仿真条件3 波束成形方向为45°时，信噪比为−20~10 dB。波束方向为45°时3种算法的BER比较如图8所示。

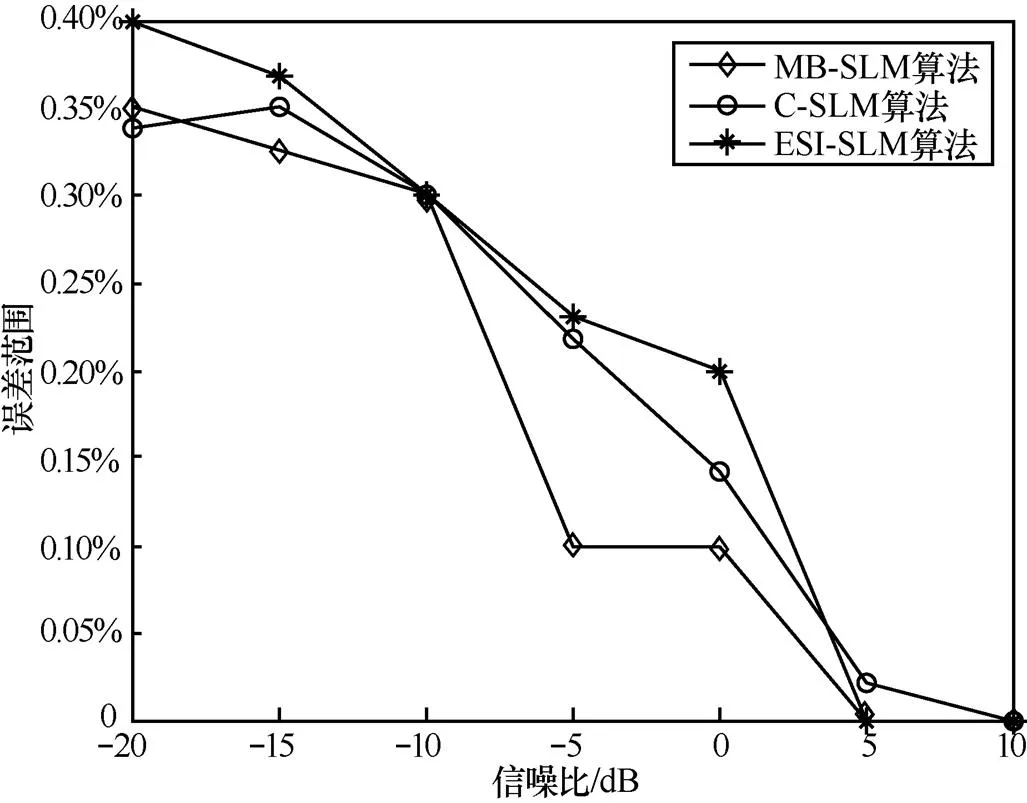
图7 波束方向为20°时3种算法的BER比较

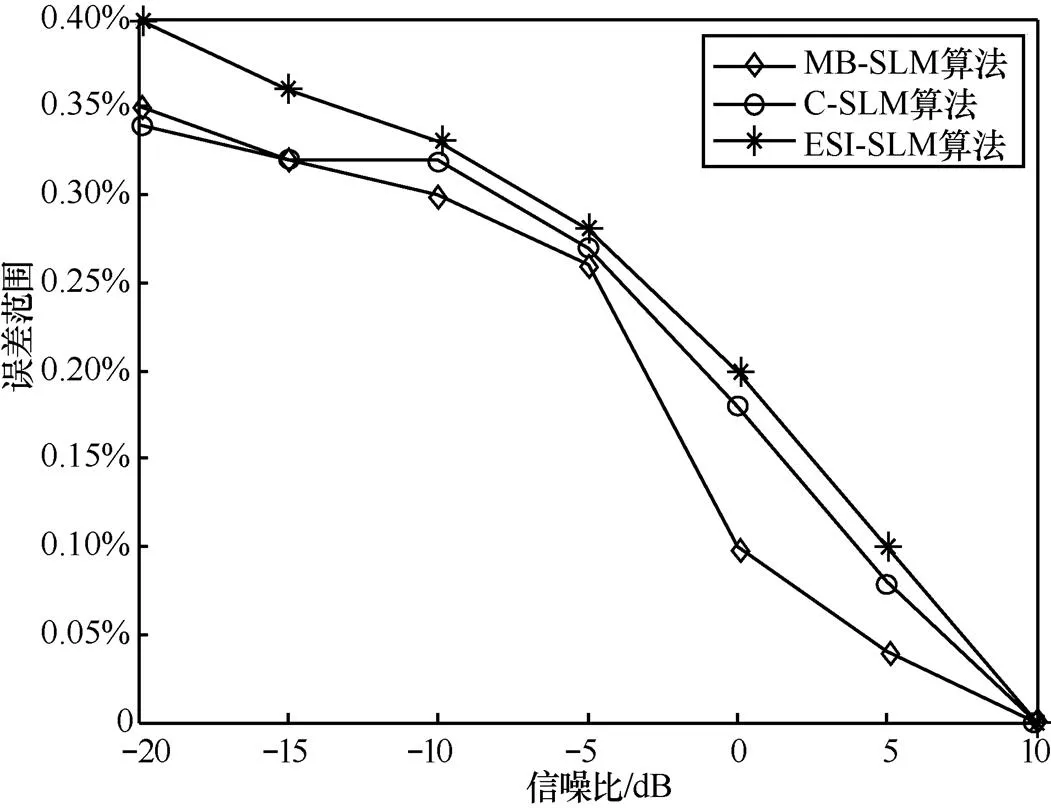
图8 波束方向为45°时3种算法的BER比较

由上述不同合成波束方向的BER仿真过程可知，本文所提的MB-SLM算法在不同的合成波束方向上均具有一定的可行性，检测的最小序列的误差范围基本在0.40%以内。

4.3 MB-MUSIC算法与C-SLM算法的PAPR抑制效果比较

实验仿真参数设置如下：相位序列均为10，信噪比为10 dB。相同相位序列的效果比较如图9所示。

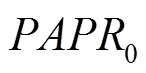
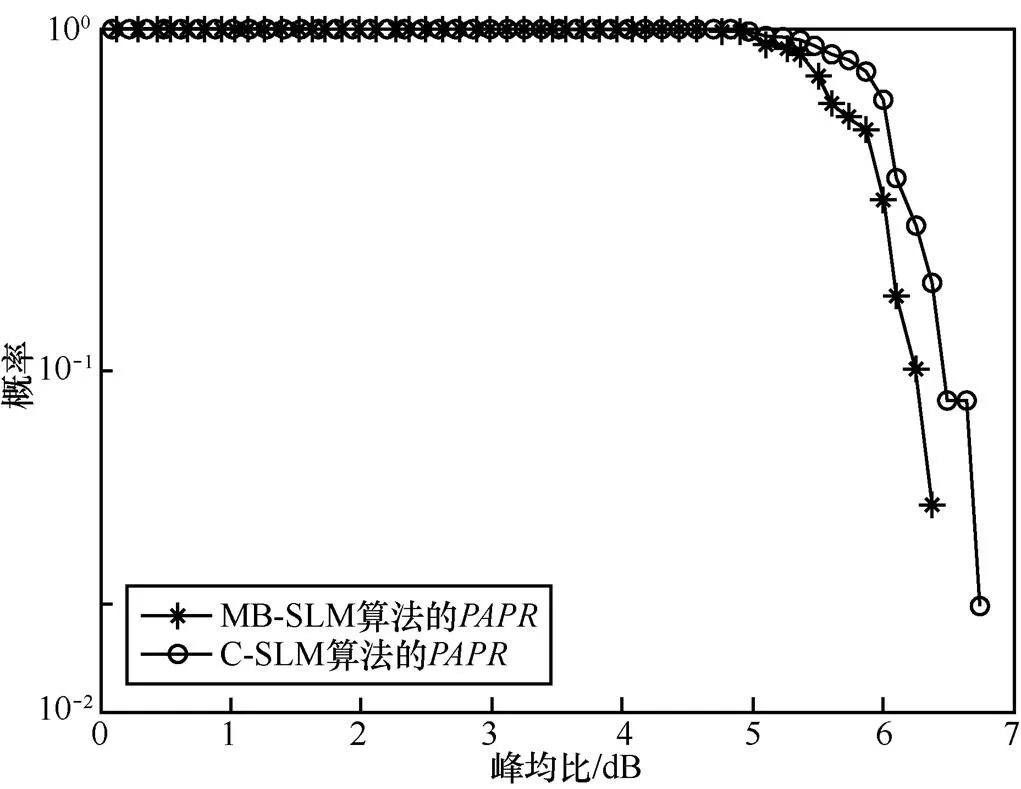
图9 相同相位序列的PAPR效果比较

4.4 MB-SLM算法的运算复杂度

设置MB-SLM算法的仿真条件和ESI-SLM算法的仿真条件一致，信噪比取10 dB，相位序列为20路；经过Matlab仿真，完成MB-SLM算法的时间大约为10×10−6，而完成ESI-SLM算法的时间为10×10−2。这充分说明MB-SLM算法的运算复杂度远低于ESI-SLM算法的运算复杂度。不同仿真参数下各种算法的运算时间如表2所示。

表2 不同仿真参数下各种算法的运算时间（单位为s）

由表1可知，MB-SLM算法在运算复杂度上较C-SLM和ESI-SLM算法的复杂度要低，MB-SLM算法的收敛速度比C-SLM算法的收敛速度快大约1%，较ESI-SLM算法的收敛速度快大约4%。

5 结束语

针对ESI-SLM算法过程中运算量大、复杂度高以及C-SLM算法中需要传输SI、降低频带利用率等问题，本文提出了一种MB-SLM算法，在一定程度上简化了运算的复杂度，避免了频带内SI的传输，提高了频带带宽的利用率。该算法只需要在信号传输端对最小的合成波束项进行SVD产生解密合成波束的密钥，然后利用矩阵分解的正交矩阵的性质，产生多路的相位序列，进而在信号经过高功率放大器后，对所需的合成波束进行解密，得到所需的合成波束。

通过实验仿真以及性能分析后可以得出，在相同的实验条件下，MB-SLM算法的运算复杂度比C-SLM算法和ESI-SLM算法要低，运行时间要快，且峰均比抑制效果较C-SLM算法大约改善0.3 dB。

[1] 王红星, 陆发平, 刘传辉, 等. 一种椭圆球面波调制信号自适应峰均比抑制方法[J]. 电子与信息学报, 2017, 39(1): 75-81.

WANG H X, LU F P, LIU C H, et al. Adaptive peak-to-average power ratio reduction method for prolate spheroidal wave function orthogonal modulation signal[J]. Journal of Electronics and Information Technology, 2017, 39(1): 75-81.

[2] ALI M, RAO R K, PARSA V. PAPR reduction in OFDM systems using clipping based on symbol statistics[C]//Electrical and Computer Engineering. 2017: 357-361.

[3] 刘剑飞, 王少影, 曾祥烨, 等. 基于改进蝙蝠算法的CO-OFDM系统峰均比抑制技术[J]. 光子学报, 2016, 45(10): 1-6.

LIU J F, WANG S Y, ZENG X Y, et al. PAPR reduction method for CO-OFDM system based on improved BAT algorithm[J]. Acta Photonica Sinica, 2016, 45(10): 1-6.

[4] ZHOU J, QIAO Y J. Low-PAPR asymmetrically clipped optical OFDM for intensity-modulation/direct-detection systems[J]. IEEE Photonics Journal, 2015, 7(3):1-8.

[5] ZHI X H, HAO H, XIAO Y. Peak-to-average power ratio analysis and reduction in transform domain communication system[C]//IEEE International Conference on Signal Processing. 2017: 1191-1195.

[6] 刘芳, 王勇. 联合星座扩展的预留子载波OFDM信号峰均比抑制算法[J]. 通信学报, 2016, 37(3): 1-7.

LIU F, WANG Y. Tone reservation technique combined with active constellation extension for PAPR reduction of OFDM signal[J]. Journal on Communications, 2016, 37(3): 1-7.

[7] SINGAL A, KEDIA D. Complexity analysis of SLM PAPR reduction schemes in wireless OFDM system[C]//International Conference on Electrical, Electronics, and Optimization Techniques. 2016: 2082-2087.

[8] JI J, REN G, ZHANG H. A semi-blind SLM scheme for PAPR reduction in OFDM systems with low-complexity transceiver[J]. IEEE Transactions on Vehicular Technology, 2015, 64(6): 2698-2703.

[9] FALLAHZADEH M, FERDOSIZADEH M. Blind SLM for PAPR reduction of Alamouti DSFBC systems[J]. IET Communications, 2017, 11(3): 451-457.

[10] LIU B C, HE Y J. Improved DBF algorithm for multichannel high-resolution wide-swath SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 1209-1225.

[11] LIU N, WANG R, ZHAO S, et al. Improved DBF algorithm for multichannel SAR with highly nonuniform sampling[C]//IEEE International Geoscience and Remote Sensing Symposium. 2016: 1424-1427.

[12] WANG Y, ZHU L. Research and implementation of SVD in machine learning[C]//International Conference on Computer and Information Science. 2017: 471-475.

[13] HWANG M J, LEE J S, LEE M S, et al. SVD based adaptive QIM watermarking on stereo audio signals[J]. IEEE Transactions on Multimedia, 2017, PP(99): 1.

[14] 柯熙政, 亢烨, 刘娟. FSO-OFDM系统中峰均比控制方法的实验研究[J]. 红外与激光工程, 2017, 46(6): 1-7.

KE X Z, KANG Y, LIU J. Experimental research on PAPR reduction algorithms in FSO-OFDM system[J]. Infrared and Laser Engineering, 2017, 46(6): 1-7.

[15] 纪金伟, 任光亮, 张会宁. 一种降低MIMO-OFDM系统PAPR的半盲SLM方法[J]. 西安电子科技大学学报, 2015, 42(5): 13-19.

JI J W, REN G L, ZHANG H N. Semi-blind SLM scheme for reducing the PAPR of MIMO-OFDM systems[J]. Journal of Xidian University, 2015, 42(5): 13-19.

Method on PAPR reduction in digital beam-forming

LIU Lu1,2, ZHAO Guoqing1

1. School of Electronic Engineering, Xidian University, Xi’an 710071, China 2. School of Telecommunication and Information, Xi’an University of Posts and Telecommunications, Xi’an 710121, China

Digital beam-forming technology is one of the key technologies in 5G communication. However, the high peak-to-average power ratio in digital beam-forming would make the power amplifier work in the nonlinear region. Nowadays, the solutions to the high peak-to-average power ratio, such as selected mapping, embedded side information selected mapping have some faults: the complexity is high, and the utilization of the bandwidth is low. A blind selected mapping method to reduce the high peak-to-average power ratio based on MUSIC algorithm was proposed. In this method, the side information was omitted, so the utilization of the bandwidth was improved. Simultaneously, the result of the peak-to-average power ratio reduction and the complexity is much more enhanced.

digital beam-forming, PAPR reduction, selected mapping, MUSIC algorithm

TN911

A

10.11959/j.issn.1000-436x.2018030

2017-07-07；

2018-01-18

陕西省科技研究发展（攻关）计划基金资助项目（No.2016YFJH2-08）

Shaanxi Province Science Research Program Foundation of China (No.2016YFJH2-08)

刘璐（1988-），女，陕西兴平人，西安电子科技大学博士生，西安邮电大学工程师，主要研究方向为信号处理、信息对抗等。

赵国庆（1953-），男，上海人，西安电子科技大学教授、博士生导师，主要研究方向为电子对抗、电子干扰等。