基于遗传算法的执行器受限PID控制∗
尹小韩 徐景硕 程春华 袁 涛
1 引言
在实际控制中,PID(比例积分微分)控制器实际上是最常用的控制器。在过去,很多典型的技术都用于PID控制参数的调整[1~4]。但是PID控制器容易受到高频噪声干扰和windup的影响[5~8]。
执行器的饱和限制是产生windup的主要原因。当闭环系统的设定值变化较大时,执行器饱和度是一个常见现象。执行器饱和的影响范围从轻微的性能下降到闭环系统的不稳定性,虽然轻微的性能下降是可以忍受的,但是不稳定是不能接受的。为此很多学者对该问题展开了研究。文献[9]基于频域技术提出了PID(比例,积分和微分)控制器的五种饱和补偿器设计方案。文献[6]提出了变结构技巧抑制了windup现象,文献[10~11]将变结构windup技巧应用到永磁同步电机的控制。文献[12]对比了几种windup技巧的效果。上述文献中所用的防饱和补偿器,由标称控制器和防饱和补偿部分组成,仅考虑了执行器受限的影响、标称控制器的效果以及最后控制的效果,然而并没有考虑控制对象的动态特性,例如超调性、上升时间等参数,并且PID参数的选择需要不断的尝试来获得。
本文利用遗传算法来获取最佳的VPID参数,同时也考虑了被控对象的动态特性。
2 问题描述
PID控制器经常用于控制需要零稳态误差的系统,同时保持对稳定时间和鲁棒性的要求。但是当系统的执行机构存在限幅时,PID控制器的性能就会受到影响,因为PID控制器中的积分项会导致windup现象。执行机构存在限幅时PID的控制如图1。
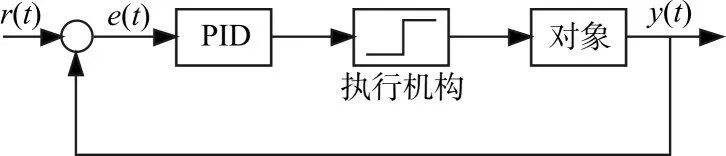
图1 执行机构限幅时的PID控制
PID控制器如下
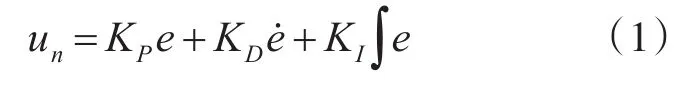
式 中 KP,KD,KI>0 为 待 设 计 的 参 数 。 当分别是执行器输出的下限和上限值),控制器就会失去它的作用,误差就会变大,虽然PID控制的本质就是根据误差消除误差,但是执行机构输出的控制量并不是所设计的un,所以闭环系统的性能就会下降,甚至不稳定。
文献[6]中采用了变结构PID设计技巧(VS⁃PID),其控制器结构如下。
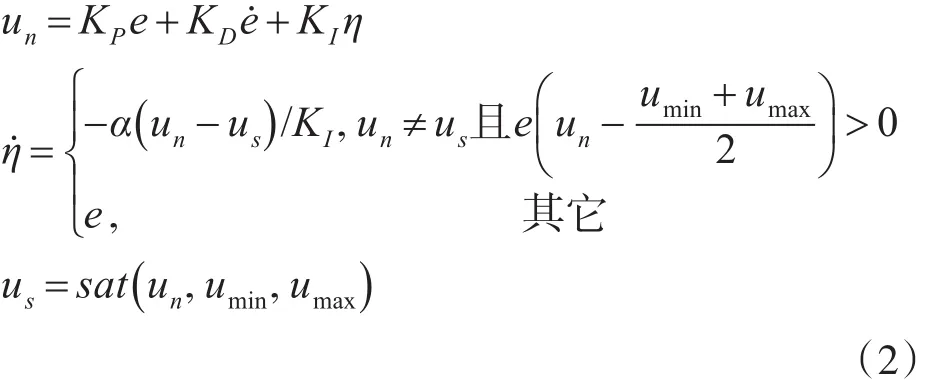
式中α>0,sat()·是饱和函数,如下。
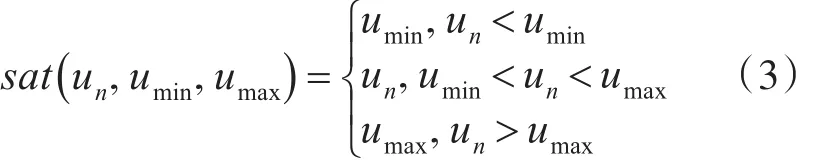
但是 VSPID 控制的性能很受 KP,KI,KD,α 值的影响。为了使系统达到良好闭环动态特性,本文接下来利用遗传算法来优化 KP,KI,KD,α 值,使VSPID的性能达到最优。
3 基于遗传算法的输入受限PID设计
遗传算法是1962年由Holland提出的,它是一种模拟自然界遗传机制和生物进化过程中优胜劣汰的一种并行随机搜索优化算法,经常用于解决优化问题。该算法从一个初始种群开始,不断重复选择、交叉和变异的过程,在种群中将具有高适应度的个体“选择”地存活下来,使进化后的种群越来越接近某一目标。
针对输入受限,本文利用遗传算法优化VSPID中的PID控制参数;另一种是直接采用遗传算法在线整定PID的参数,以便在控制量出现限幅时改变PID的参数来保持控制效果。
采用遗传算法设计时,需要构建恰当的目标函数。为了进一步改善VSPID的动态特性,采用误差绝对值时间积分、上升时间和超调量作为目标函数,其形式如下。
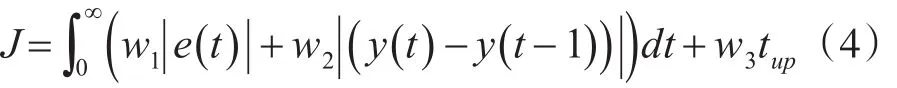
式中tup为上升时间,e(t)为系统t时刻的误差,y(t) 为系统 t时刻的输出值,w1,w2,w3为权值,大于0。
注:当(y (t)-y(t -1) )<0时,表示出现超调,此时要将w2| (y (t)-y(t -1) )|纳入目标函数;若(y (t)-y(t -1) )>0时,表示在上升阶段,此时不将w2| (y (t)-y(t -1) )|纳入目标函数。
交叉概率和变异概率设计如下。
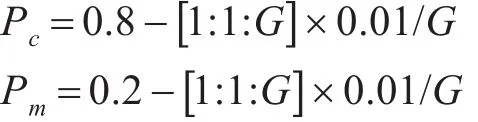
式中G为进化的代数。
4 仿真实例
仿真对象采用文献[6]中的电炉模型,如下。
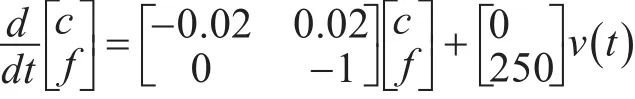
式中v(t)是输入电压,它的范围为[0 V,10V] ,f(t)是灯丝温度,c()t是室内温度。
控制目标是使电炉室内温度达到1500℃。仿真结果如图2~6,图2是系统控制后电炉室内温度,从图中可以看出,本文的设计方案几乎没有超调,并且上升时间很快;图3是控制器的输出量;图4是本文的目标函数进化曲线;图5是PID控制参数进化曲线;图6是α参数进化曲线。
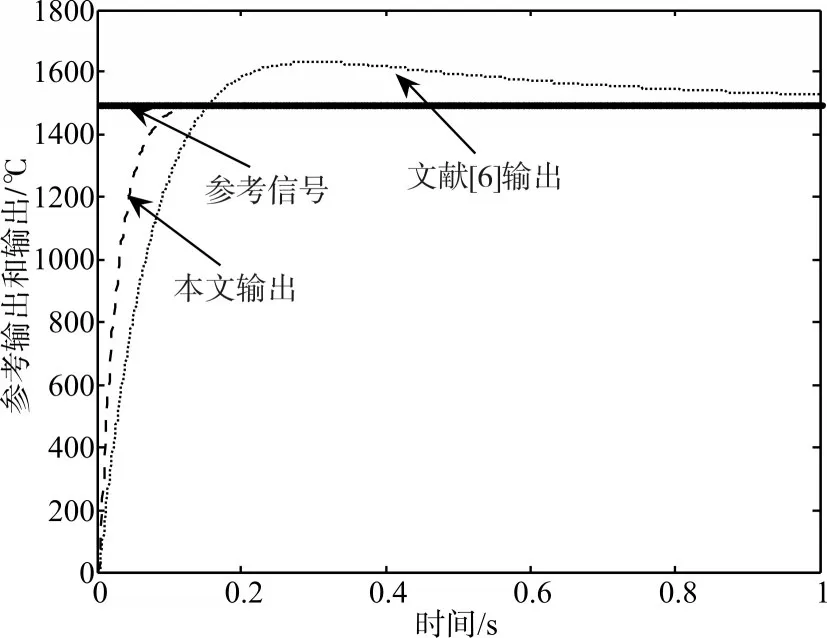
图2 电炉室内温度
5 结语
针对文献[6]中VPID设计时参数选择较困难,并且设计时没有考虑闭环系统的动态特性,本文利用遗传算法,将误差绝对值时间积分、上升时间和超调量作为目标函数,确定了使闭环系统性能达到最优的KP,KD,KI,α参数。最后利用该设计方案,在控制执行机构受限情况下,可以很快地、无超调地将电炉的室内温度调节到目标温度。
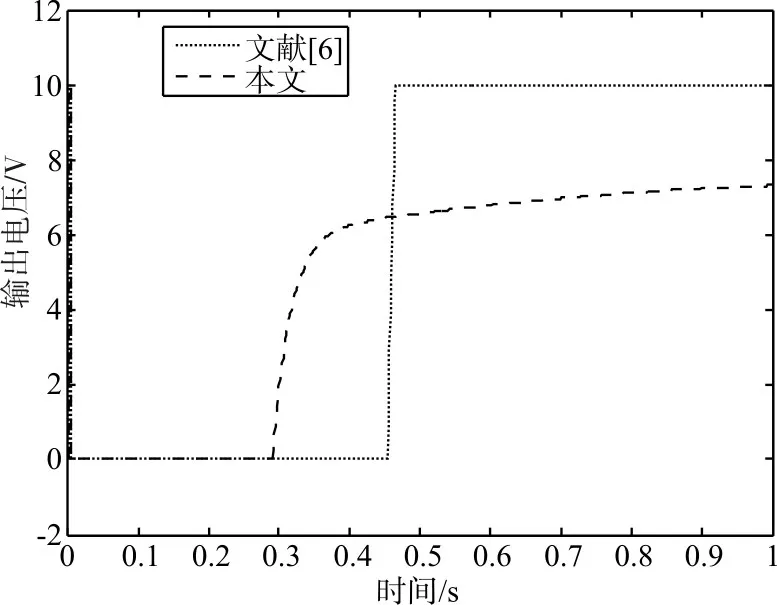
图3 控制器输出电压
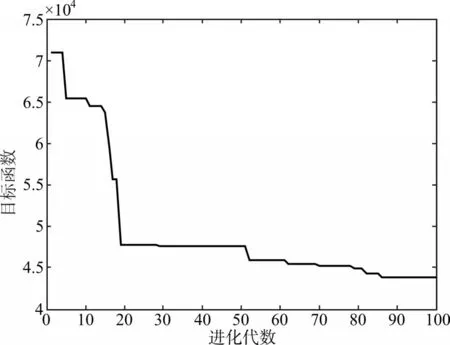
图4 目标函数进化曲线
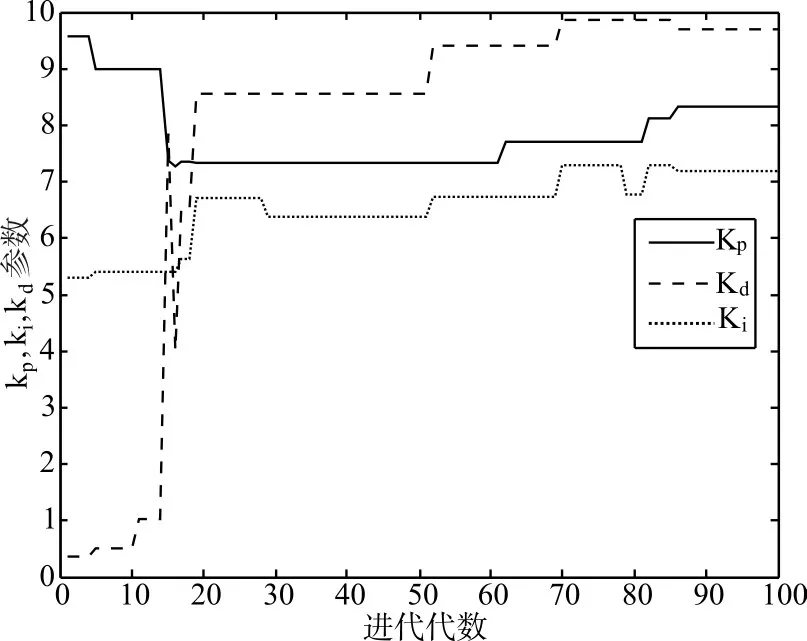
图5 KP,KD,KI参数进化曲线
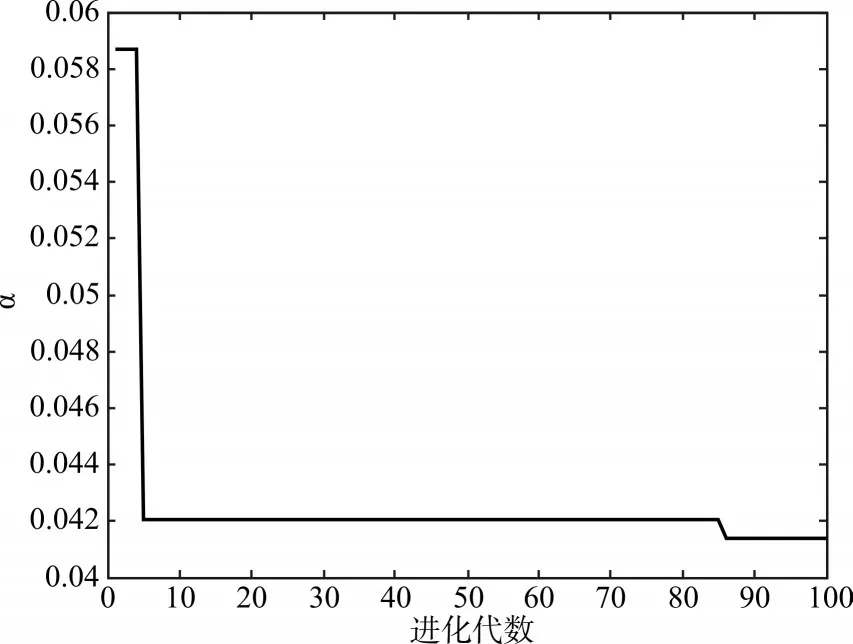
图6 α参数进化曲线
[1]N.Tan,D.P.Atherton.Design of Stabilizing PI and PID Controllers[J].International Journal of System Science,2006,37(8):543-554.
[2]Y.Okada1,Y.Yamakawa,T.Yamazaki,S.Kurosu.Tun⁃ing Method of PID Controller for Desired Damping Coeffi⁃cient[C]//SICEAnal Conference,Kagawa University,Ja⁃pan,2007(9):795-799.
[3]游有鹏,龚华军.PID参数专家校正器[J].自动化仪表,1994(2):5-8
[4]王伟,张晶涛,柴天佑.PID参数先进整定方法综述[J].自动化学报,2000,26(3):347-355
[5]C.Bohn a,D.P.Atherton.An Analysis Package Compar⁃ing PID Anti-Windup Strategies[J].IEEE Control Sys⁃tems,1995,15(2):34-35.
[6]A.S.Hodel,C.E.Hall.Variable-Structure PID Control to Prevent Integrator Windup,IEEE Transactions on In⁃dustrial Electronics,2001,48(2):442-451.
[7] A.Visioli,Modified Anti-Windup Scheme for PID Controllers[C]//IEEE Proc.Control Theory and Ap⁃pl.,2003,150(1):49-54.
[8] R.J.Mantz and H.D.Battista,Comments on Vari⁃able-Structure PID Control to Prevent[J].IEEE Transac⁃tions on Industrial Electronics,2004,51(3):736-738.
[9]K Hui,CWChan.New design methods of actuator satura⁃tion compensators for proportional[J].integral and deriva⁃tive controllers,1997,211(4):269-272.
[10]于艳君,柴凤,高宏伟等.基于Anti-Windup控制器的永磁同步电机控制系统设计[J].电工技术学报,2009,24(4):66-71.
[11]Ming YANG,_Li NIU,Dianguo XU.Antiwindup design for the speed loop PI controller of a PMSM servo system[J].Turkish Journal of Electrical Engineering&Com⁃puter Sciences,2013(21):1318-1327.
[12] SRIKANTH B.COMPARISON OF ANTI-WINDUP SCHEMES[J].International Journal of Research in Sci⁃ence and Technology,2015,1(5):157-166.

