基于多特征优化的海面目标识别技术∗
但 波 邹小海
1 引言
雷达高分辨距离像(High Resolution Range Pro⁃file,HRRP)是用宽带雷达信号获取的目标散射点子回波在雷达射线上投影的向量和,它提供了目标散射点沿距离方向的分布情况,是目标重要的结构特征[1~2]。不同舰船目标的强散射点分布与其结构紧密相关,因此,利用目标HRRP可为海面目标特征提取与识别提供丰富的信息。
针对舰船目标的识别早期多基于窄带雷达,而窄带信息有限,除简单的大小分类外,很难提供更多的目标信息。而随着装备的发展,高分辨雷达可以提供舰船目标的结构信息,这为类型识别提供了可能。
但是HRRP具有幅度、方位和平移三方面的敏感性。针对方位敏感性,文献[3]在识别前,选取了以不发生越距离单元走动(Migration Through Reso⁃lution Cell,MTRC)效应作为间隔对舰船目标的HRRP进行了非相干平均。文献[4]在训练过程中,将每个舰船目标样本中隔2个抽取一个作为训练样本。文献[5]将统计概率模型用于刻画目标一维距离像随姿态角的变化趋势,进行自适应分帧。
但是上述方法还存在以下不足:
1)MTRC效应应用于HRPP存在适用性问题
对目标角域进行等间隔划分,虽然在一定程度通过累加平均可以增强自身项,减小交叉项的影响,但散射点MTRC效应是ISAR成像的条件,因此等间隔分帧的限制条件直接用于目标HRRP分帧存在分帧角度不确定性问题,同时也不能准确反映出目标的统计特性变化。
2)采用统计特性对目标角域进行划分的方法存在局限性
分帧准则不清晰,在一定条件下(样本数目较小或样本太长)存在无法自适应确定各个目标的帧总数目和分类效果较差的问题。同时针对舰船目标,提出的统计特性假设可能会与实际情况存在一定差异,有可能降低统计模型的分帧效果。
皮尔逊相关系数代表了两个向量的相似性,方位间隔越小的HRRP之间的相关系数越大。其物理意义明确,因此通过可设定一个概率差门限对目标回波HRRP进行自适应分帧,可认为在该方法下划分的每帧样本统计特性是近似一致的。
作为雷达目标识别中的核心环节,特征提取阶段所提取的特征好坏直接影响到整个识别系统性能的优劣。特征提取主要分为非参数化方法和参数化方法。
非参数特征提取方面,文献[3]利用舰船的HRRP提取了船长、离散性、对称性、中心矩等作为特征进行了目标识别研究。文献[4]利用傅里叶-梅林变换,得到了稳定的平移不变性和尺度不变性特征向量。文献[6]基于舰船目标HRRP,提取了其高阶谱特征。文献[7]针对舰船目标全极化HRRP,提取了熵特征、能量特征和散射矩阵相似性参数概率特征。
参数特征提取方面,西安电子科技大学的杜兰等研究人员,提出了对不同类型的距离单元采用不同的概率模型描述,从而建立了基于Gamma和Gaussian Mixture两种分布形式的独立算分布复合模型[8-9]。文献[10]提出了一种基于Relax散射点特征的舰船目标识别方法,文献[11]在对GTD散射模型近似处理的基础上提出了一种估计散射中心类型参数的新方法。
但是现有参数化模型均是根据训练样本构造一个能反映数据分布特点的概率模型,然后估计模型参数,再用模型进行分类。由于参数化模型方法是数据驱动的,因此泛化能力欠佳,特别是在用于各型舰船分类时,面对如此种类繁多的目标,模型适应性会大打折扣,因此本文重点考虑非参数特征提取方法。
本文在前期自适应分帧的基础上,利用非参数方法提取目标HRRP的结构特征、变换域特征等多种特征。然后,选用合适特征评估方法,优选出可分性较高的特征。最后,根据优选后的特征,实现对3类舰船目标的识别。基于舰船目标转台数据的仿真结果表明,与传统的利用实距离像等间隔角域划分方法相比较,该方法可以有效改善识别性能。
2 均匀分帧法存在的若干问题研究
2.1 均匀分帧法
均匀分帧是指以目标回波不发生MTRC为限制条件,将一个目标均匀分为若干份子目标,子目标包含目标的所有方位角,对各子目标提取目标特征信息,建立数据库。将一帧内的距离像序列认为是同一个角域,每个角域的散射点特征可描述目标各部分的特征。
2.2 均匀分帧存在的问题
根据光学区散射中心模型理论,在散射中心不发生MTRC的方位角范围内,目标的散射点模型基本不变。为了消除方位敏感性,传统方法一般对整个训练数据采用等间隔角域划分方位帧,实际上不发生MTRC效应条件为[12]

式中Δφm为雷达相对目标转动角度,λ为波长,l为目标横向尺寸。
以舰船类目标为例,当 f=1GHz,l=100m,代入式(1)计算可得不发生MTRC的角度约等于0.043°,对大部分散射点来说,角度可以适当增加。若分帧按照0.5°角度进行,则每个舰船全角域下样本一共会有720帧,单次像按照每个0.1°计算,每帧共有5个距离像序列,样本数据较少,且继续细化分帧会影响系统识别效率。
实际上,应该从目标距离像散射单元间的实际统计特性出发进行分帧。因此提出基于舰船目标HRRP皮尔逊相关系数的自适应分帧处理方法。
3 舰船目标HRRP皮尔逊相关系数自适应处理方法
3.1 平均距离像的皮尔逊相关系数
皮尔逊相关系数计算特征与特征间的相关性的公式如下。
设 fx与 fy为两个特征,分别为 fx={fx1,fx2,…,fxn} ,fy={fy1,fy2,…,fyn} ,n 是 样 本 个数,皮尔逊相关系数为

3.2 利用皮尔逊相关系数分帧步骤
利用皮尔逊相关系数分帧步骤如图1所示。

图1 皮尔逊相关系数分帧方式
以下为分帧详细步骤:
步骤1:设定概率差门限 δi(i =1,2,…,M ) ,i为目标类别数目,设定每帧最小样本数目输入HRRP序列,并对数据作预处理,得到目标距离像序列 Ti=,k 是样本回波总数。
步骤2:按式(2)计算目标Ti第1次回波与第2次回波关系值 ρ=ρ21,如果 ρ>δi,计算第1次回波与第3次回波的关系值 ρ31,更新两次回波的加权系数后与δi比较,直到前l( )l≥α次皮尔逊相关系数平均值≤δi,则认为前l-1次回波构成的散射点模型未发生改变,相对应的距离像可以分为一帧。
步骤3:剔除已合并的方位帧,将后续的距离像序列提取前置,将HRRP序列更新为更新样本总回波数目为k-l+1,重复步骤2;
步骤4:迭代中止条件,当迭代计算到样本最后一个回波xk-l+1时,若此时距离像皮尔逊相关系数平均值≤δi,则将这部分回波合并为一帧;否则,将xk-l次回波及之前的回波记为一帧,最后一帧的样本xk-l+1记为一帧。
一般来说对于不同目标设置的门限δ并不相同,度量标准是根据散射点模型不变的最大回波次数间相差的度数来衡量的,依此设定门限来对整个距离像序列的自适应帧域划分。同时由于对训练数据进行角域自适应分帧是一个离线过程,因此训练数据的分帧不影响识别时的运算效率,并且由于自适应分帧可以减少目标的模板数目,因此识别时匹配运算量会有所降低,可以减少目标识别的时间。
4 基于舰船目标HRRP的多特征提取与优化设计
4.1 结构特征提取
第m次HRRP实样本可表示为

其中上标“T”表示转置运算,xn(m)表示第n个距离单元的第m次复回波。上式表示的时域特征,其直观地反映了散射点分布和目标的尺寸等物理结构特性。
基于HRRP样本的时域信号,可进一步提取与目标物理特性有关的直观特征,其表达了对特定参量情况下目标距离像的直观或视觉理解,本文重点考虑以下直观结构特征:尺度特征、强散射中心数目、两个最强散射中心间距离、最强散射中心距目标前端的距离。
1)尺度特征
主要的尺度特征为目标的最大长度,是目标识别时最直观的几何形状特征,可通过计算超过一定门限的距离单元所占据的单元数除以舰船对应方位角的余弦,可以得到目标的最大长度,其准确度与角度估计相关,它是目标识别中最直观的几何形状特征。
设目标的雷达波入射余角为α,则目标的尺度特征表示为其中,γ是加权因子,r是目标的径向长度。

2)目标强散射中心数目
提取距离像轮廓中峰值的数目,用来刻画目标的结构特征。设分割后的目标一维距离像采样幅值序列为经概率统计后确定一个峰值门限,可通过峰值搜索算法自动获得目标的强散射中心数目,其主要反映了目标的强散射点个数。
3)散射中心间距离
散射中心间距离主要包括两个最强散射中心间距离(Peak distances,DPK)和最强散射中心距目标最前端的距离(Distance of largest peak to near range edge,DEP),二者主要反映了目标强散射中心距离位置之间的对应关系。
4.2 变换域特征提取
通过对HRRP进行合适变换,有助于挖掘区分性更强且维度更小的变换域特征,本文重点考虑高阶中心矩(Cetral moment)特征。
设{x(n),n=1,2,...,N}为距离像,N 为距离单元数,则归一化距离像可表示为

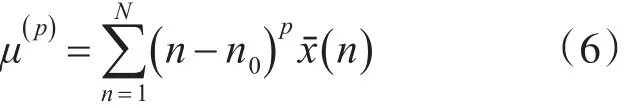
其中n0表示一阶原点距,即归一化距离像的散射重心。
中心矩提供了目标的几何结构信息,例如对称性等,具有平移、旋转及尺度不变性,适用于识别对象较简单的情况。各阶中心矩在分类识别中的作用不同,例如二阶中心矩实质上反映了各散射中心与散射重心离散的程度。值得注意的是,二阶及高阶中心矩的距离像平移分量是以原点矩为参考点来进行补偿的,因此具有平移不变特征,可作为特征向量:

其中,pmax代表中心矩的最高阶数。由于不同阶中心矩之间不是正交的,存在信息冗余,当阶数大于10时,高阶中心矩提供的有用信息急剧减少,且有可能形成干扰,使识别率下降,因此实际应用中中心矩阶数不宜取得过高。由于偶数阶中心矩比奇数阶中心矩具有更强的稳定性,因此重点考察2阶中心矩(Second-order Central Moment,SCM)作为特征向量。
上述结构特征和变换域特征从不同的角度反映目标特性,具有一定的信息互补性。例如可以利用尺度特征识别尺寸相差较大的目标,可用于目标的初分类。同时,因为不同目标的中心矩特征和散射中心数目也不同,因此提取相关特征能对目标尺度特征进行有效的补充。
4.3 多特征优化设计
经特征提取后每个目标在任意方位角可以提取多个特征,但并不是所有特征对分类识别都能发挥积极作用,多特征间可能存在不同程度的相关性和信息冗余,因此必须进行特征评估与选择,筛选出可分性强且冗余性小的特征子集,然后进行多特征联合识别处理。
特征评估的基本任务是通过一个定量的准则来衡量目标特征对目标分类的敏感程度,选取最有利于识别的特征,从而实现数据的压缩与计算量的减少。特征选取是否得当将直接影响到识别算法的效率、处理时间、所需数据量以及扩展性。如果能选取适当特征并组合,则能显著改善识别性能。
本文选用类内、类间距离的准则函数,研究所优选特征的类别间可分性,通过分析特征子集内部的特点来衡量其好坏,最后将可分性较高的特征用于目标的分类识别。
5 特征有效性分析
通过对不同方位角下不同的目标特征进行可分性分析,可有效判断特征的有效性。选用常用的类内、类间离差矩阵作为可分性度量的准则,可分性判据值如下:

其中SB和Sw分别为类内和类间离差矩阵,J越小,则说明选用的特征使得不同类别的可分性越差,反之,越好。
由于目标尺度特征主要是用于目标初分类,因此 这 里 分 别 以 0°~6°、25°~31°、50°~56°与75°~81°为例对剩余四类特征可分性进行判断。
图2中B、Q、H分别代表滨海战斗舰、驱逐舰、护卫舰,舰船具体参数见6.1说明。由图可知特征值DEP、DPK和SCM在方位角域中可分性值较大,而峰值点特征的可分性值较小。因此,DEP特征、DPK特征和SCM特征可用于目标识别。
6 实验与分析
6.1 仿真实验数据说明
研究用的数据来自于国外某雷达目标散射仿真软件,计算了某型濒海战斗舰(B,长127.5m,宽31.2m,高 32.5m)、某型护卫舰(H,长 98.8m,宽9.8m,高27.3m)和某型驱逐舰(Q,长135.8m,宽14.6m,高26.4m)共3类舰船目标的转台数据。选用雷达中心频率10GHz,带宽150MHz。数据产生选用方位角 0°~360°(0°正对船头,顺时针为角度增加方向),单次样本间隔0.5°,掠射角为0°。

图2 三类舰船特征在不同方位角域下的可分性值
6.2 仿真分析利用SVM算法目标分类步骤
目标分类步骤如下。
步骤一:按3.2中分帧方式对目标进行角域划分,将目标的实距离像作为训练距离像进行预处理,从第一个目标回波开始每间隔7回波取一次回波作为样本作为测试距离像,以此方式选取可以包含目标各个方位的距离像情况。
步骤二:将预处理后的数据进行特征提取,除尺度特征外其余特征输入到SVM分类器中,核参数ζ经过多次训练选择为0.5。
步骤三:将测试距离像也进行预处理与特征提取后根据尺度特征先对目标进行预分类,然后将提取的特征向量输入到SVM分类器中进行测试。
随着训练HRRP分帧总数的变化,3类舰船目标的平均识别率曲线如图3所示。

图3 训练HRRP帧总数变化下的平均识别率曲线
表1所示为三种方法的运算时间以及平均识别率。
其中对实距离像采用等间隔分帧的方法,当分帧总数为432时,三类舰船目标的平均识别率可达到73%,此时每帧包含5个回波样本。对实距离像进行特征提取后采用等间隔分帧的方法分帧总数为270时,三类舰船目标的平均识别率可达到78%。而对实距离像进行特征提取后采用皮尔逊相关系数的分帧总数为180时,三类舰船目标的平均识别率达到90.2%。由于特征提取等间隔分帧的方法较实距离像等间隔分帧的方法可以更加准确反映出目标间特征存在的差异,因此前者比后者的最高平均识别率要高5%,同时由于提取的特征向量要远小于原始实距离像的特征维数,因此识别处理的时间从原来的1.81s减少到0.72s;而通过采用皮尔逊相关系数自适应分帧后,突出了各目标的自身统计特性的变化规律,因此识别率进一步提升了12.2%;因为帧数的减少,识别时间进一步减少到0.54s。
对三类舰船目标采用相同门限的识别率曲线如图4所示。
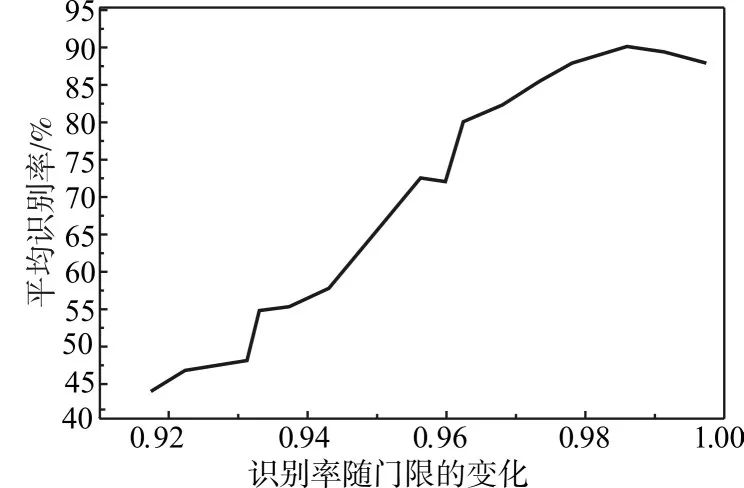
图4 门限变化下的平均识别率曲线
由图4可知当门限升高时由于帧数划分的更加细致,对目标不同方位角下的识别更加细致,目标的识别率持续上升,当门限达到0.985时,目标的识别率达到峰值为88.6%,此后由于帧数划分过于细致导致每帧内样本数减少,导致识别时无法消除自身项的影响,识别率降低。由此可见,在选择门限时并非越高越好,应根据目标自身特性选择适当的门限,这样识别效果才能达到最佳。
7 结语
本文首先分析了等间隔分帧方法对目标识别影响的具体原因。基于舰船目标回波,利用皮尔逊相关系数自适应地对舰船目标HRRP进行角域划分,降低了识别时模板匹配数量和识别时间。然后在分帧的基础上进一步对特征的提取与优选进行了探讨,主要提取包括L、P、DEP、SCM及DPK在内的五类目标特征,通过对特征的可分性进行研究,优选出可分性高的特征。最后利用SVM分类器中对优选特征进行识别实验,与传统的方法相比较,该方法可以有效改善识别性能。
[1]BAI Xue-ru,Feng Z,BAO Zheng.High-resolution radar imaging of space targets based on HRRPseries[J].IEEE Trans.on Geoscience and Remote Sensing.2013,7(3):1-13.
[2]DU Lan,LIU Hongwei.WANG Penghui.Noise robust ra⁃dar HRRP target recognition based on multitask factor analysis with small training data size[J].IEEE Trans.on Signal Processing,2012,60(7):3546-3559.
[3]刘先康,梁菁,任杰等.基于HRRP中心矩特征的舰船目标识别[J].计算机工程与应用,2009,45:195-198.
[4]刘江波,席泽敏,卢建斌等.一种舰船目标一维距离像识别的新方法[J].海军工程大学学报,2010,22(1):62-66.
[5]Jacobs SP,O'Sullivan A.Automatic target recognition us⁃ing sequences of high resolution radar range-profiles[J].Aerospace and Electronic Systems,IEEE Transactions ,2000,36(2):364-381.
[6]孙菲,梁菁,任杰等.一种基于高阶谱特征的舰船目标识别方法[J].舰船科学技术,2011,33(7):105-108.
[7]郭雷,肖怀铁,赵宏钟等.宽带全极化雷达目标HRRP极化特征提取与优选[J].自然科学进展,2009,19(7):784-792.
[8]DU Lan,LIU Hongwei,BAOZheng,ZHANGJunying.A two-distribution compounded statistical model for radar HRRPtarget recognition[J].IEEE Transactions on signal Processing,2006,54(6):2226-2238.
[9]DU Lan,LIU Hongwei,BAOZheng.Radar HRRPstatis⁃tical recognition:parametric model and model selection[J].IEEE Transactions on Signal Processing,2008,56(5):1931-1944.
[10]王锦章,魏存伟,刘先康等.基于Relax散射点特征提取的舰船目标识别方法[J].电子科技,2011,24(4):8-11.
[11]任双桥,姜斌,王宏强等.GTD散射模型参数解调耦估计技术[J].现代雷达,2006,28(5):47-52.
[12]杜兰.雷达高分辨距离像目标识别方法研究[D].西安:西安电子科技大学,2007.

