黄灯期间首停车及末行车行驶参数分析
付川云,刘海玥
(1. 西南交通大学,交通运输与物流学院,成都610031;2. 综合交通运输智能化国家地方联合工程实验室,成都610031)
0 引 言
黄灯启亮时,直行车道上的首停车(第一辆选择停止的车辆)和末行车(最后一辆选择继续通行的车辆)最有可能陷入两难区。根据两难区的定义,黄灯期间首停车及末行车行驶参数与两难区边界确定密切相关[1]。因此,探究黄灯期间首停车及末行车行驶参数,对揭示两难区分布及缩小或消除两难区范围具有重要的意义。
关于黄灯期间首停车及末行车行驶参数,国外学者主要关注了感知反应时间,减速度,以及加速度。感知反应时间包括停车和行驶感知反应时间,且二者常被假设为相等[2]。众多学者分析了停车感知反应时间(以下简称感知反应时间)的范围、均值、百分位值等,并认为对数正态分布或贝塔分布能较好地拟合感知反应时间[3,4]。关于减速度,美国交通工程师协会推荐其取值为3.05 m/s2[5],而美国国家公路与运输协会标准的推荐值是3.41 m/s2[6]。一些文献也给出了减速度的百分位值[7],且其中85%位值均比美国交通工程师协会和美国国家公路与运输协会标准的推荐值大。与前面两个行驶参数不同的是,加速度常被假设为0,然而,这与实际情况不符。
尽管国内学者对驾驶人反应时间开展了一定的研究[8],但关于黄灯启亮时驾驶人感知反应时间的研究鲜见报道。对于减速度,国内文献大多直接采用美国交通工程师协会或美国国家公路与运输协会标准的推荐值。同样地,加速度也常取定值0。
综上,国内外关于黄灯期间首停车及末行车行驶参数的研究较少,且不系统。因此,本文以有无倒计时信号交叉口为调查地点,通过视频观测法采集黄灯期间首停车及末行车行驶参数,并比较分析这些参数的描述统计值和拟合分布。
1 数据采集
1.1 首停车及末行车行驶参数定义
(1)首停车行驶参数
① 黄灯启亮时至停车线距离,黄灯启亮时首停车沿车道线平行方向上至停车线的距离。
② 黄灯启亮时速度,以区间速度代替。
③ 感知反应时间,指黄灯启亮与刹车灯启亮之间的时间差。
④ 减速度,等于黄灯启亮时速度与制动时间的比值。
(2)末行车行驶参数
除黄灯启亮时至停车线距离和速度外,还包括:
① 进入时间,指黄灯启亮与末行车越过停车线的时间差。
② 加速度,由其余三个参数确定,计算公式为:

式中:a为加速度(m/s2);XC指黄灯启亮时至停车线距离(m);v是黄灯启亮时速度(m/s);t为进入时间(s)。
1.2 视频观测
黄灯期间首停车及末行车行驶参数通过视频观测方法获取。在哈尔滨市内选择了具备良好视距、过街行人流量小、相交道路限速为60 km/h及以上、进口道上游存在人行天桥等条件的4个有倒计时和2个无倒计时信号交叉口作为观测点。对每个观测点仅拍摄一次且均选在晴天的下午2~6点进行拍摄。最终,共获得24 h的视频数据。各观测点的详细信息及视频观测的具体情况详见文献[9]。
1.3 数据提取
凭借Pure Codec Player播放器和图林白板软件,提取黄灯期间首停车及末行车行驶参数。删除黄灯启亮前便制动及无法确认刹车灯是否启亮的首停车的相关信息。此外,删除闯红灯末行车和少量常规公交车的相关信息。更多关于数据提取的细节,详见文献[9]。最终,所提取的样本数,如表1所示。
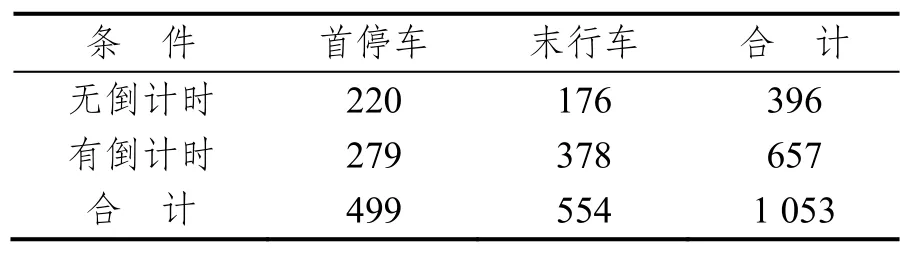
表1 所提取的样本数Tab.1 The sample size
2 首停车行驶参数分析
2.1 黄灯启亮时至停车线距离
黄灯启亮时首停车至停车线距离的描述统计值如表2所示。Levene’s检验结果表明,有无倒计时条件下黄灯启亮时首停车至停车线距离的方差无显著性差异,F(1,497)=0.105,P=0.746(显著性水平为0.05,下同)。于是,由等方差t检验可知,这两种条件下其均值无显著性差异,t=1.960,p=0.051。
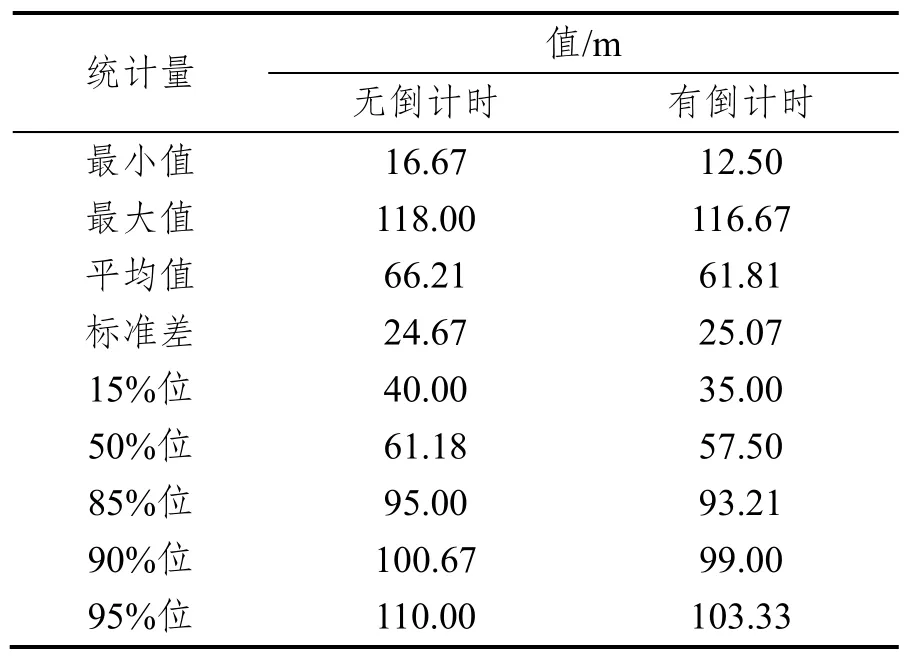
表2 黄灯启亮时首停车至停车线距离的描述统计值Tab.2 Descriptive statistics of the distance to the stop line at the start of yellow time of the first-to-stop vehicles
根据样本数据的特点,选择约翰逊SB分布、广义极值分布、韦布尔3P分布和对数皮尔森3分布进行拟合,得到参数估计结果见表3。Kolmogorov-Smirnov(K-S)检验结果表明,这四种分布均可用于拟合有无倒计时条件下黄灯启亮时首停车至停车线距离,且最佳拟合分布均是约翰逊SB分布。
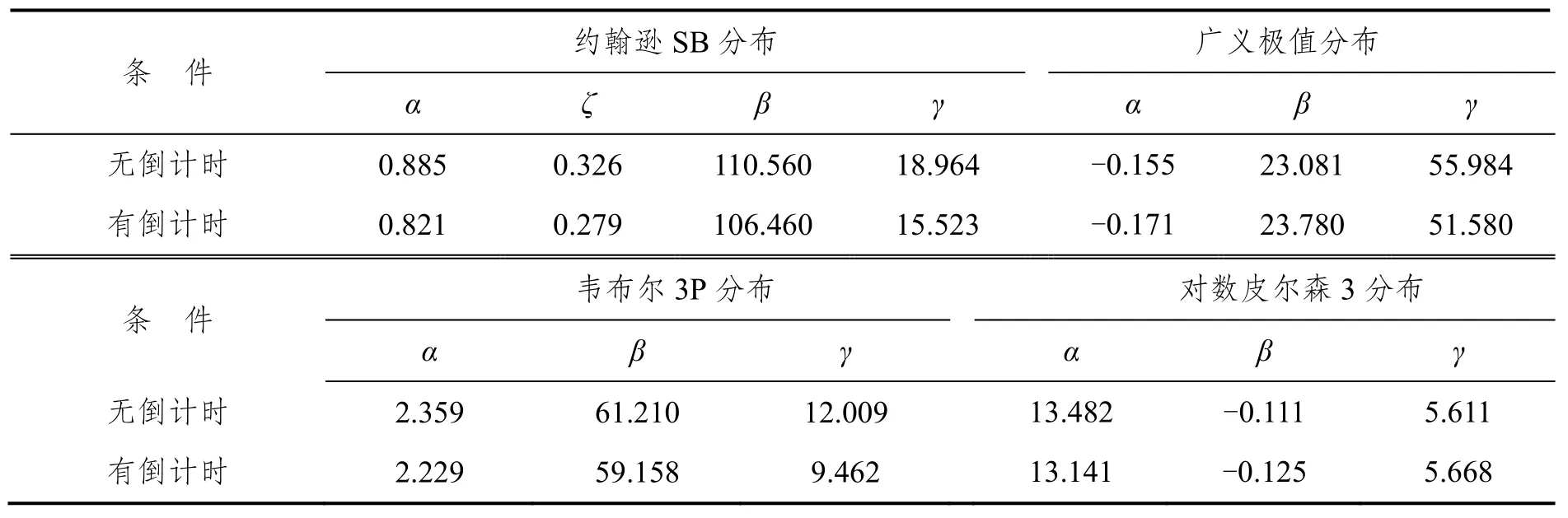
表3 拟合分布中参数估计结果Tab.3 Parameters of the fitted distributions (distance to the stop line)
2.2 黄灯启亮时速度
黄灯启亮时首停车速度的描述统计值,如表4所示。Levene’s检验结果表明,有无倒计时条件下黄灯启亮时首停车速度的方差具有显著差异性,F(1,497)=6.397,p=0.012。因此,由异方差t检验可知,无倒计时条件下黄灯启亮时首停车的平均速度显著大于倒计时条件下的平均速度,t=2.134,p=0.033。
类似地,选择贝塔分布、伽马分布、韦布尔3P分布以及正态分布拟合样本数据,得到参数估计结果见表5。K-S检验结果表明,这四种分布均可用于拟合有无倒计时条件下黄灯启亮时首停车速度,且伽马分布是无倒计时条件下的最佳分布,而贝塔分布是倒计时条件下的最佳分布。
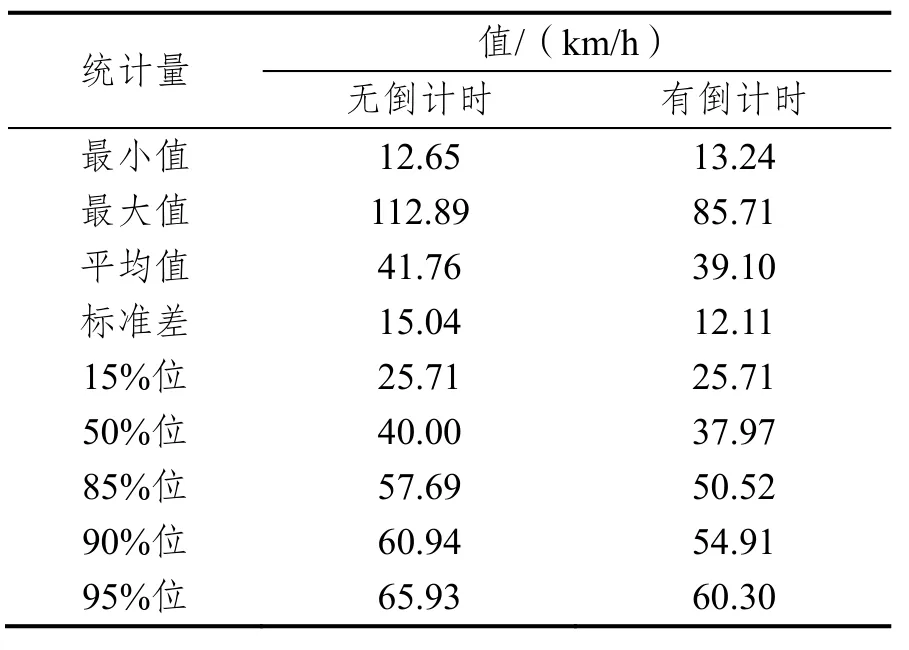
表4 黄灯启亮时首停车速度的描述统计值 Tab.4 Descriptive statistics of the speed at the start of yellow time of the first-to-stop vehicles
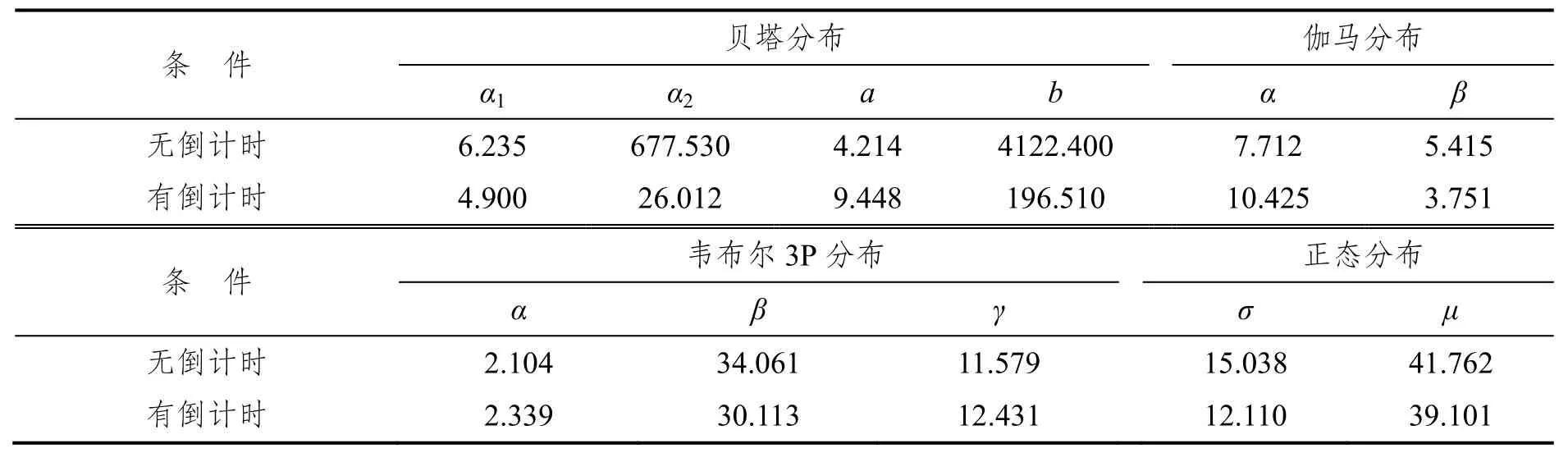
表5 拟合分布中参数估计结果Tab.5 Parameters of the fitted distributions (speed)
2.3 感知反应时间
感知反应时间的描述统计值,如表6所示。Levene’s检验结果显示,有无倒计时条件下感知反应时间的方差有显著性差异,F(1,497)=10.810,p=0.001。于是,由异方差t检验可知,这两种条件下感知反应时间均值有显著性差异,t=-2.988,p=0.003。
根据样本数据的特点,选择对数逻辑斯谛分布、对数正态分布、韦布尔分布和伽马分布进行拟合,得到参数估计结果见表7。K-S检验结果表明,无倒计时条件下感知反应时间服从对数逻辑斯谛分布、对数正态分布或伽马分布,且对数逻辑斯谛分布是最佳分布;倒计时条件下感知反应时间服从韦布尔分布和伽马分布,且韦布尔分布是最佳分布。
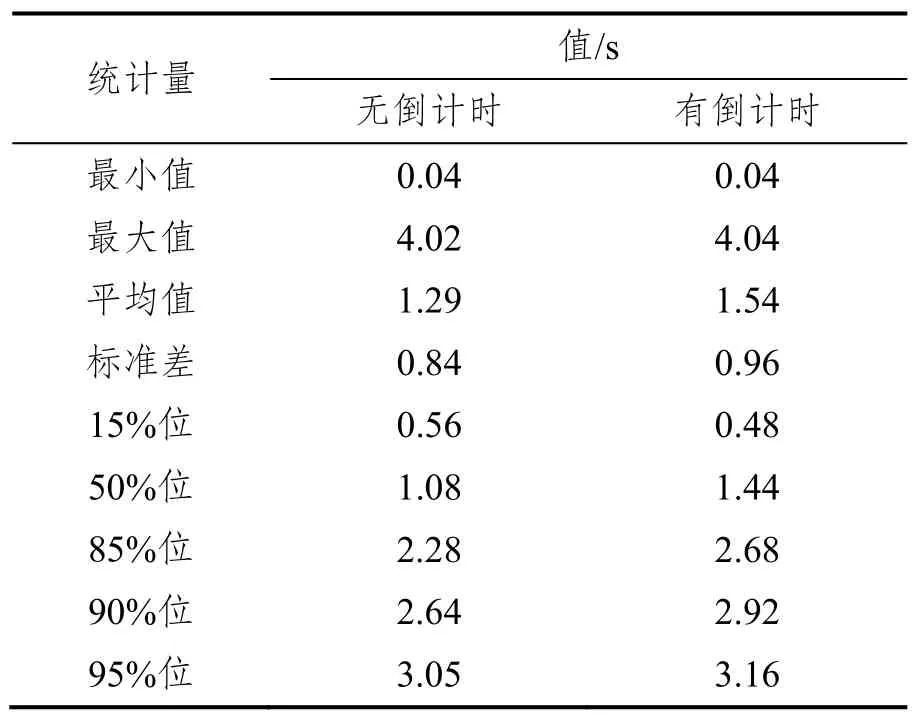
表6 感知反应时间的描述统计值Tab.6 Descriptive statistics of the perception-reaction time

表7 拟合分布中参数估计结果Tab.7 Parameters of the fitted distributions (perception-rection-time)
2.4 减速度
减速度的描述统计值,如表8所示。Levene’s检验结果显示,有无倒计时条件下减速度的方差无显著性差异,F(1,497)=2.036,p=0.154。因此,由等方差t检验可知,这两种条件下减速度的均值无显著性差异,t=1.732,p=0.084。
根据样本数据的特点,选择贝塔分布、对数逻辑斯谛3P分布、对数正态3P分布和伽马分布进行拟合,得到参数估计结果见表9。K-S检验结果表明,这四种分布均可拟合有无倒计时条件下减速度,且对数逻辑斯谛3P分布是无倒计时条件下的最佳分布,而对数正态3P分布是倒计时条件下的最佳拟合分布。
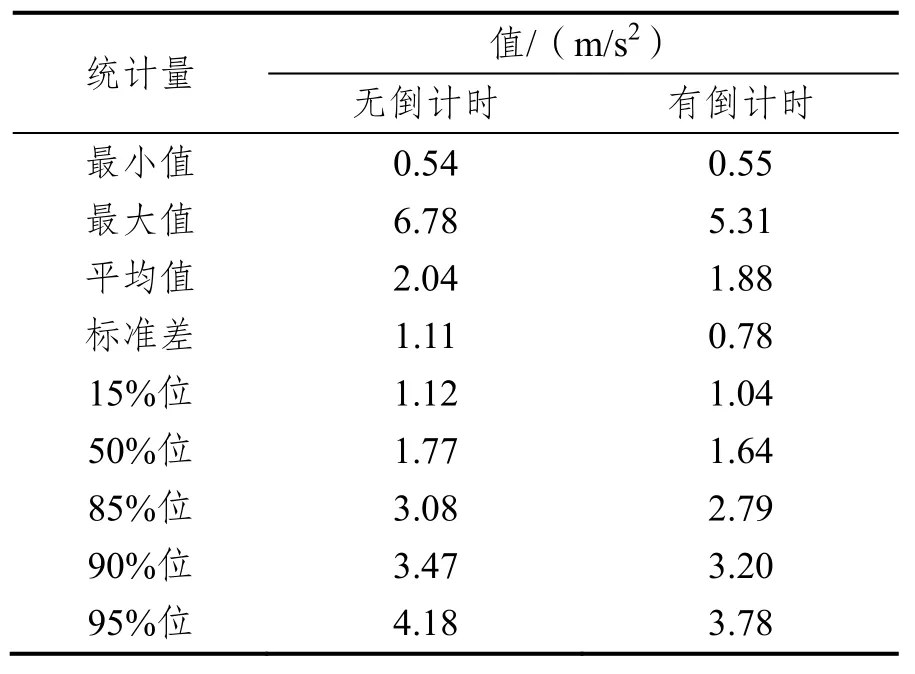
表8 减速度的描述统计值Tab.8 Descriptive statistics of the deceleration rate
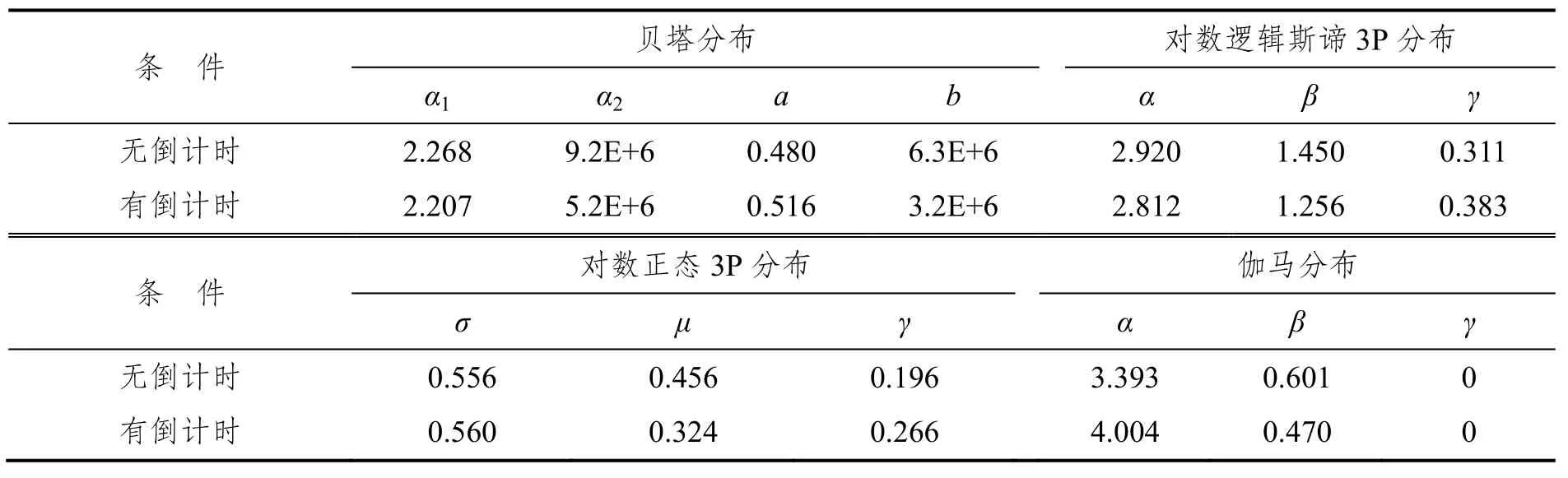
表9 拟合分布中参数估计结果Tab.9 Parameters of the fitted distributions (deceleration rate)
3 末行车行驶参数分析
3.1 黄灯启亮时至停车线距离
黄灯启亮时末行车至停车线距离的描述统计值,如表10所示。Levene’s检验结果显示,有无倒计时条件下黄灯启亮时末行车至停车线距离的方差无显著性差异,F(1,552)=0.117,p=0.732。于是,由等方差t检验可知,这两种条件下黄灯启亮时末行车至停车线距离的均值具有显著性差异,t=6.934,p<0.0001。
根据样本数据的特点,选择广义极值分布、伽马分布、对数皮尔森3分布和对数正态分布进行拟合,得到参数估计结果见表11。K-S检验结果表明,这四种分布均可拟合无倒计时条件下黄灯启亮时末行车至停车线距离,且广义极值分布是最佳分布,但无分布可用于拟合倒计时条件下黄灯启亮时末行车至停车线距离。
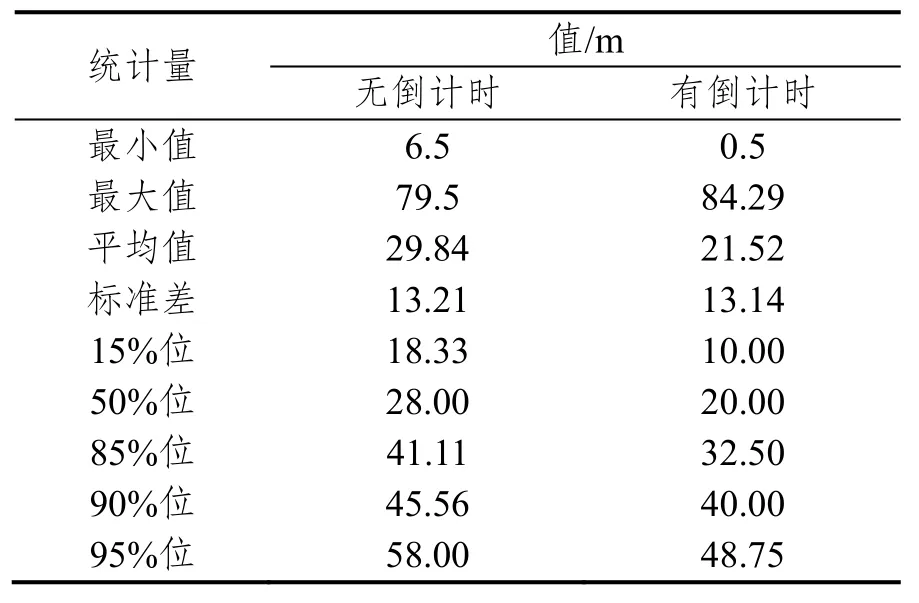
表10 黄灯启亮时末行车至停车线距离的描述统计值Tab.10 Descriptive statistics of the distance to the stop line at the start of yellow time of the last-to-go vehicles
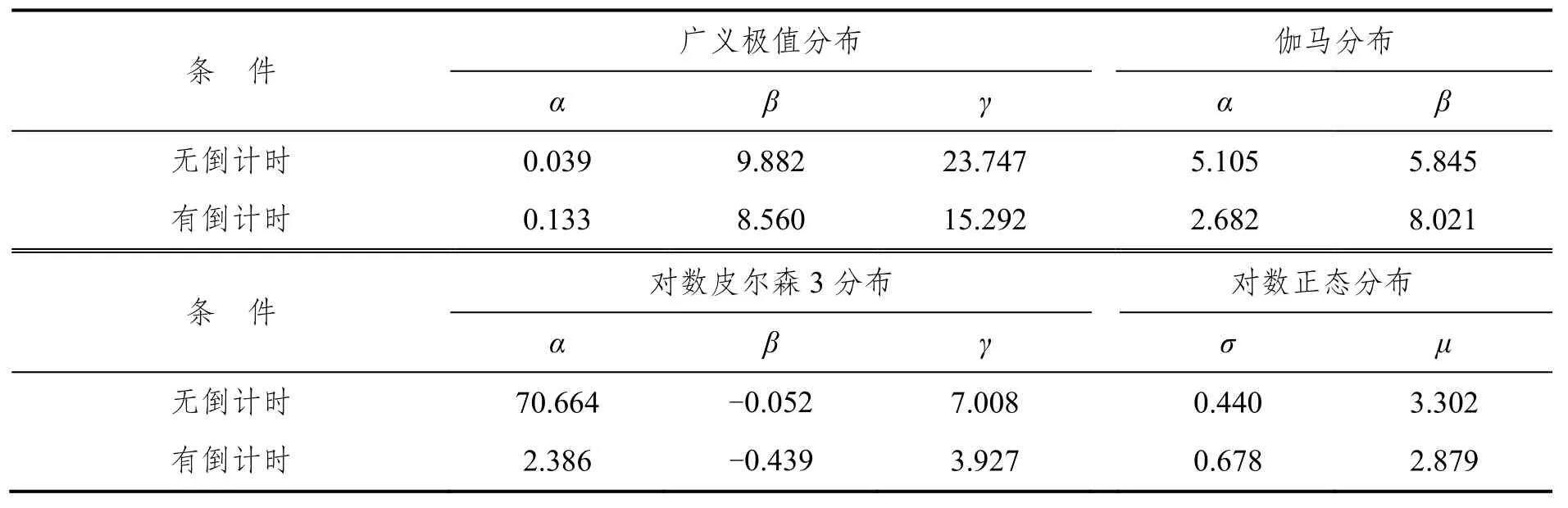
表11 拟合分布中参数估计结果Tab.11 Parameters of the fitted distributions (distance to the stop line)
3.2 黄灯启亮时速度
黄灯启亮时末行车速度的描述统计值,如表12所示。Levene’s检验结果显示,有无倒计时条件下黄灯启亮时末行车速度的方差无显著性差异,F(1,552)=2.957,p=0.086。因此,由等方差t检验可知,这两种条件下黄灯启亮时末行车速度的均值无显著性差异,t=-0.262,p=0.794。
根据样本数据的特点,选择约翰逊SB分布、韦布尔3P分布、贝塔分布和正态分布进行拟合,得到参数估计结果见表13。K-S检验结果表明,有无倒计时条件下黄灯启亮时末行车速度服从约翰逊SB分布、贝塔分布或韦布尔3P分布,且最佳分布均为约翰逊SB分布。
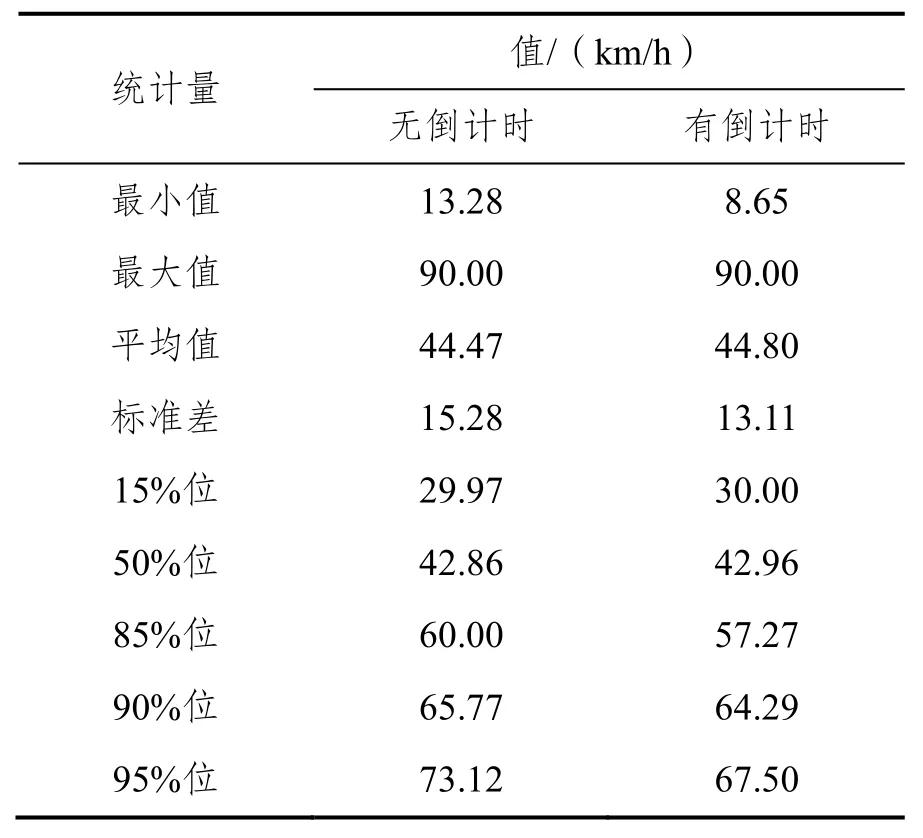
表12 黄灯启亮时末行车速度的描述统计值Tab.12 Descriptive statistics of the speed at the start of yellow time of the last-to-go vehicles
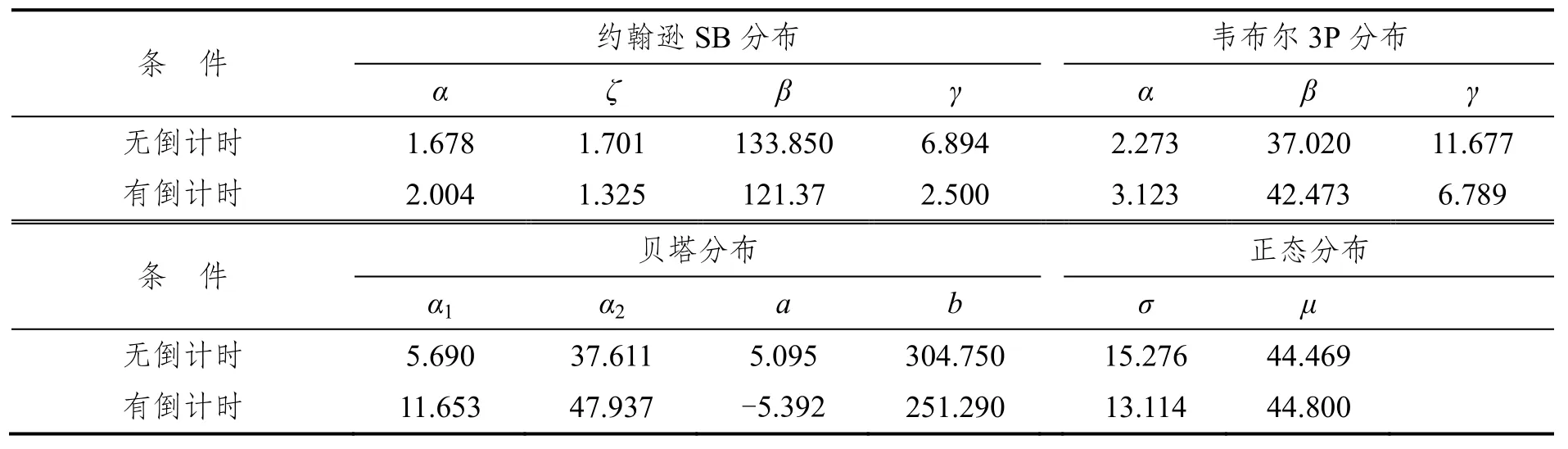
表13 拟合分布中参数估计结果Tab.13 Parameters of the fitted distributions (speed)
3.3 进入时间
进入时间的描述统计值见表14。Levene’s检验结果表明,有无倒计时条件下进入时间的方差无显著性差异,F(1,552)=0.287,p=0.592。于是,由等方差t检验可知,这两种条件下进入时间的均值具有显著性差异,t=8.952,p<0.0001。
根据样本数据的特点,选择约翰逊SB分布、对数皮尔森3分布、贝塔分布和韦布尔分布进行拟合,得到参数估计结果见表15。K-S检验结果表明,这四种分布均可拟合有无倒计时条件下进入时间,且韦布尔分布是无倒计时条件下的最佳分布,而约翰逊SB分布是倒计时条件下的最佳分布。
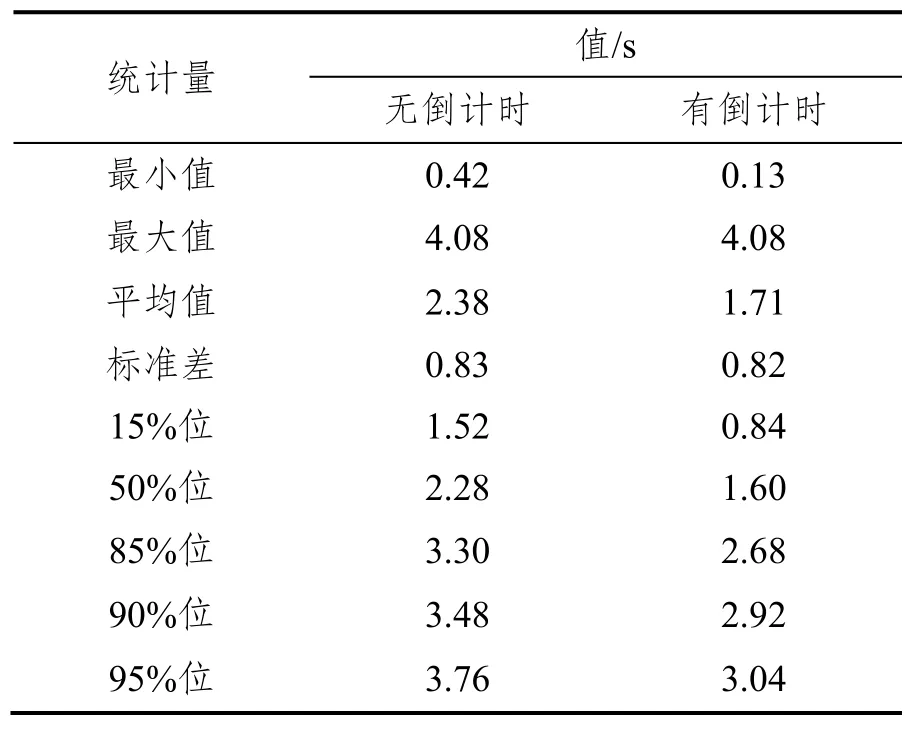
表14 进入时间的描述统计值Tab.14 Descriptive statistics of the entry time
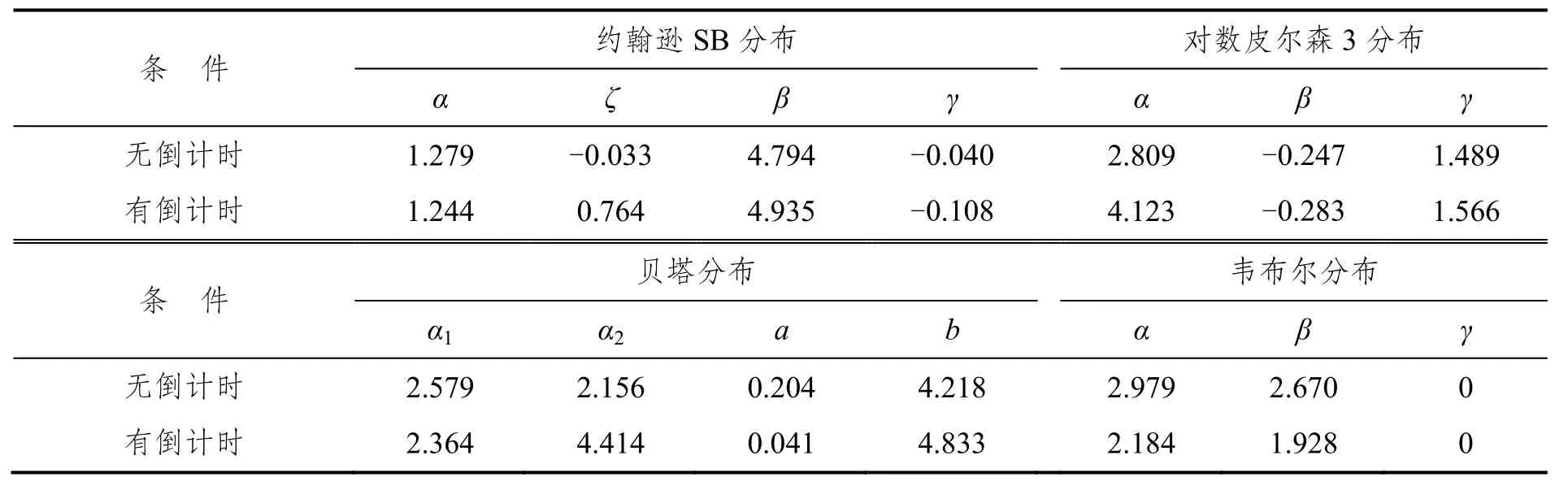
表15 拟合分布中参数估计结果Tab.15 Parameters of the fitted distributions (entry time)
3.4 加速度
减速度的描述统计值,如表16所示。Levene’s检验结果显示,有无倒计时条件下加速度的方差具有显著性差异,F(1,552)=16.383,p<0.0001。因此,由异方差t检验可知,这两种条件下加速度的均值无显著性差异,t=-1.186,p=0.236。
根据样本数据的特点,选择对数逻辑斯谛3P分布、对数正态3P分布、广义极值分布和正态分布进行拟合,得到参数估计结果见表17。K-S检验结果表明,这四种分布均可拟合有无倒计时条件下加速度,且对数逻辑斯谛3P分布均是最佳分布。
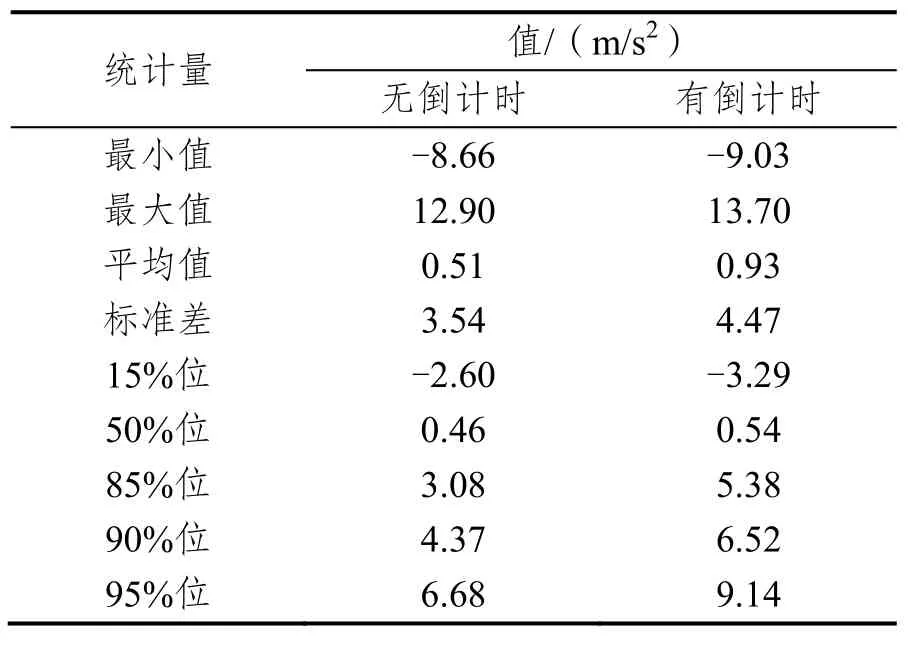
表16 加速度的描述统计值Tab.16 Descriptive statistics of the acceleration rate
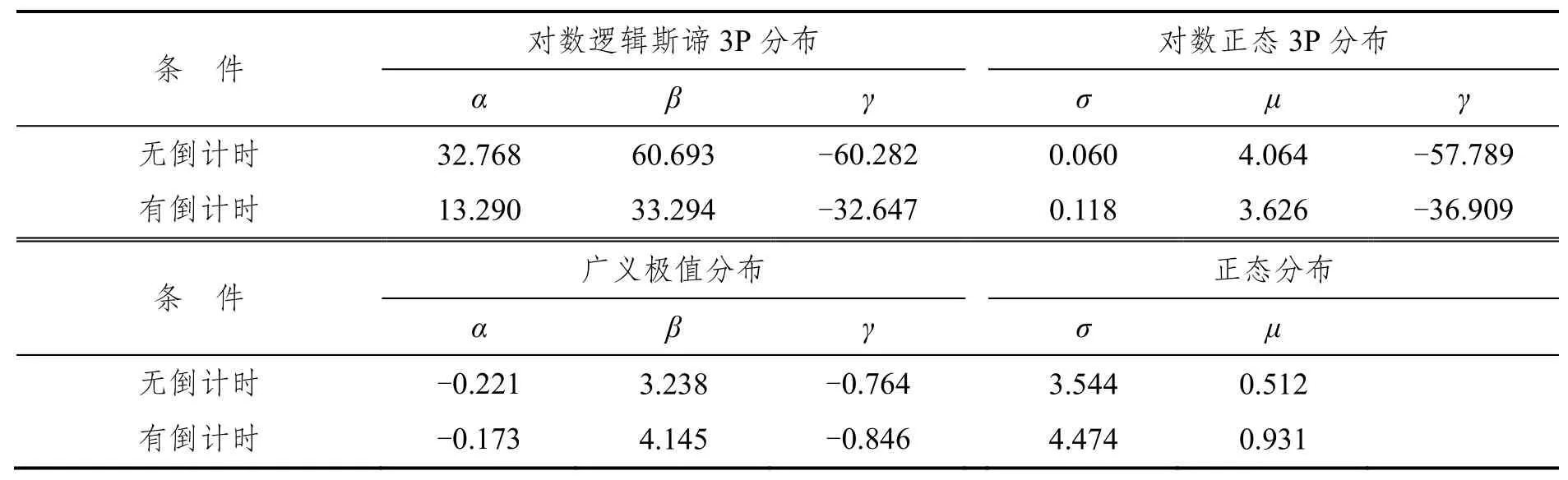
表17 拟合分布中参数估计结果Tab.17 Parameters of the fitted distributions (acceleration rate)
4 结 论
本文利用视频观测方法采集了有无倒计时条件下黄灯期间首停车及末行车行驶参数(包括黄灯启亮时至停车线距离、速度、感知反应时间、减速度、进入时间、加速度),对这些参数进行了描述统计分析,探讨了倒计时对首停车及末行车行驶参数的影响,并分析了有无倒计时条件下上述参数的拟合分布。假设检验结果表明,倒计时对首停车黄灯启亮时速度、感知反应时间及末行车黄灯启亮时至停车线距离、进入时间有显著影响。Kolmogorov-Smirnov检验结果显示,有无倒计时条件下黄灯期间首停车及末行车行驶参数的最佳拟合分布各异。
本文研究成果可为有无倒计时条件下两难区边界确定及黄灯期间车辆行驶行为模拟奠定数据及理论基础。然而,由于采集数据的精度有限且无倒计时条件下样本数据偏少,故关于有无倒计时条件下黄灯期间首停车及末行车行驶参数的统计分析结果有待后续研究进一步完善。
[1] ZHANG Y, FU C, HU L. Yellow light dilemma zone researches:a review[J]. Journal of Traffic and Transportation Engineering(English Edition),2014,1(5):338-352.
[2] LI Z. Dynamic dilemma zone modeling and its protection[D].Cincinnati:University of Cincinnati,2011.
[3] SETTI J R,RAKHA H,EL-SHAWARBY I. Analysis of brake perception-reaction times on high-speed signalized intersection approaches[C]. Proceedings of 2006 IEEE Intelligent Transportation Systems Conference. Toronto:2006:689-694.
[4] GOH P K, WONG Y D. Driver perception response time during the signal change interval[J]. Applied Health Economics and Health Policy,2004,3(1):9-15.
[5] ITE. Traffic engineering handbook(the seventh edition)[M]. New Jersey:John Wiley & Sons,Inc.,2016.
[6] CLICK S M. Application of the ITE change and clearance interval formulas in North Carolina[J]. ITE Journal,2008,78(1):20-24.
[7] GATES T J, NOYCE D A, LARACUENTE L, et al.Analysis of driver behavior in dilemma zone at signalized intersections[J]. Transportation Research Record:Journal of the Transportation Research Board,2007,(2030):29-39.
[8] 柴琳果,蔡伯根,王化深,等. 车联网中驾驶员反应时间实时估计方法[J]. 交通运输系统工程与信息,2016,16(5):71-78.
[9] FU C, ZHANG Y, BIE Y, et al. Comparative analysis of driver’s brake perception-reaction time at signalized intersections with and without countdown timer using parametric duration models[J]. Accident Analysis and Prevention,2016,95:448-460.

