滑枕挠曲变形分析及补偿力拟合研究*
李 阳 陈再良 朱志豪
(苏州大学机电工程学院,江苏 苏州 215021)
TH6920落地镗铣床主要由床身、工作台、立柱、滑枕和主轴箱等部件组成。其中,滑枕在主轴箱中的最大伸出量为1 200 mm。滑枕在工作中形成力学范畴里的悬臂梁模型,在主轴滑枕组件自重及工作时所受切削力作用下,滑枕头部会发生一个向下的挠曲变形,称为“滑枕低头”现象[1]。而且随着滑枕伸出长度的变化,其重心也发生相应移动,导致机床产生非线性变形误差,直接影响被加工工件的加工精度和表面质量。本文运用有限元软件ANSYS Workbench分析滑枕组件自重条件下滑枕行程和所受铣削力对滑枕头部挠度的影响,探讨了在用平衡重锤补偿主轴箱倾斜误差的基础上,有利于对滑枕挠曲变形实现同步、实时补偿的拉杆补偿方式,并结合数值拟合的理论,建立了不同主轴转速下滑枕伸出量与补偿力的对应关系。
1 主轴滑枕组件的有限元建模
在创建几何模型的过程中,要考虑有限元分析的特点,对分析对象的外形和大小进行必要的忽略和简化[2]。具体做法是将主轴滑枕结构中存在的一些尺寸较小的细节,如倒角、圆角、螺纹孔、退刀槽等忽略,再将处理后的模型导入ANSYS Workbench中,而将滑枕端盖、轴承、流水套、隔套等以质量单元的形式导入有限元模型中[3]。这样既有利于网格划分,确保模型分析精度,又可以节省计算机存储容量,提高运算速度。
用三维设计软件创建的滑枕组件模型如图1,滑枕尺寸为460 mm×510 mm×3 790 mm,铣轴长1 966 mm,外径为260 mm(承载轴承处),镗杆长3 485 mm,直径为200 mm。滑枕材料为球墨铸铁QT600-3,铣轴材料为20Cr,镗杆材料为38CrMoAl。通过网格无关化操作,确定Element Size为0.04 m,共得到154 360个节点,85 279个单元。
2 滑枕组件变形分析
2.1 滑枕自重产生的挠曲变形
滑枕在工作时,伸出主轴箱之外,符合悬臂梁模型,受滑枕组件自身重力的作用,滑枕端部会产生向下的挠曲变形。滑枕伸出长度不同,其重心位置也会发生对应改变,致使滑枕头部挠度呈非线性变化。采用全约束施加在滑枕外部静压导轨处,将主轴等附件的重量施加在滑枕内部安装轴承处,并将标准重力加速度施加于滑枕模型的-Z方向,经过软件多次计算分析,得到如图2所示的滑枕组件变形云图。

在滑枕长度方向上每隔100 mm取一个点进行分析,得到镗杆在未伸出状态下,滑枕头部挠度与滑枕行程的关系曲线如图3所示。从图3可以看出,当滑枕行程在100~700 mm之间时,滑枕头部挠曲变形较小,而当滑枕行程大于700 mm后,滑枕重心逐渐脱离主轴箱,当重心越过临界点时产生巨大倾覆力矩,使滑枕头部挠度急剧增大。


2.2 铣削力产生的挠曲变形
滑枕挠曲变形大小与加工过程中所受载荷大小有关。在TH6920镗铣加工中心的各种加工方式中,铣削加工使滑枕负载较大,且逆铣时主要载荷方向与滑枕重力方向一致,使滑枕挠曲变形更为显著,由铣削经验公式[4]:
(1)
式中:d为刀盘直径;P为主轴电动机功率;n为主轴转速;Fz为主铣削力;Fx为径向铣削力;Fy为轴向铣削力。由于x和y方向受到的铣削力相对z向较小,且方向不与重力方向一致,因此只对滑枕z向所受铣削力及其产生的挠曲变形进行分析计算。已知:P为71 kW,n为0~2 000 r/min,d取标准刀盘直径系列中的常用值315 mm,分别计算主电动机转速为500、1 000和2 000 r/min时,滑枕端部承受的z向铣削力,如表1所示。
表1 3种主轴转速对应的z向铣削力

主轴转速n/(r/min)铣削力Fz/N50086091000430520002152
在有限元模型的铣轴末端分别施加上述3个铣削力,经过ANSYS Workbench多次分析计算,得到如图4所示的不同铣削力作用下滑枕z向头部挠度。

3 挠曲变形的补偿方法
滑枕在垂直方向上的挠曲变形主要是由自重及铣削力引起的,因此补偿的基本思路是给主轴滑枕组件施加一种载荷,使其产生的变形与重力和铣削力产生的变形相抵消。目前,国内外普遍采用平衡重锤法[5]补偿主轴箱的倾斜误差,尽量减小主轴箱倾斜导致的滑枕头部挠度变化。本文探讨的是在此方法基础上,有利于实现同步实时补偿的拉杆补偿方式[6]。
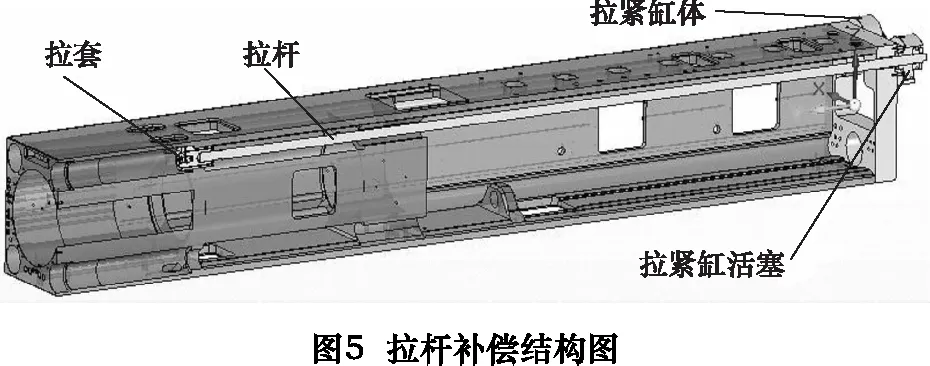
3.1 拉杆补偿基本原理
如图5所示,两细长拉杆对称安装于滑枕内部,拉杆补偿力大小由液压油缸调节,油缸伸缩由伺服电液比例阀控制[7],以实现滑枕挠曲变形的实时补偿。根据图3,当滑枕行程大于700 mm时,滑枕头部挠度急剧增大,所以结合考虑附件头拉爪的安装,将拉套安装于距离滑枕头部端面627 mm处,以补偿头部挠度急剧增大的部分。
3.2 补偿拉力计算及拟合
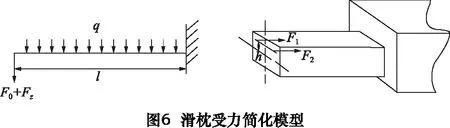
根据图3和图4可知,滑枕自重和铣削力对其头部挠度变化具有重要影响,所以为补偿滑枕的挠曲变形,需要考虑主轴转速与滑枕行程的不同,给拉杆施加相应的补偿力。将滑枕受力简化成如图6所示的悬臂梁模型,臂长l即滑枕行程,均布载荷q表示滑枕自重。主轴组件的重力通过轴承传递在滑枕上,由于第二组轴承到滑枕头部的距离大于滑枕的最大行程,所以受力作用点不在悬臂梁模型上。F0表示第一组轴承对滑枕的作用力,铣削力Fz与F0方向一致,共同作用在滑枕头部。F1、F2分别表示两根拉杆的补偿力,其大小相等,二力作用点到中性层的距离都为h,相对中性层产生的弯矩为M。
为补偿滑枕头部的挠曲变形,必须使弯矩M与滑枕所受作用力q、F0和Fz产生的合挠度为零。即[8]:
(2)
式中,弯矩:
M=2F1h
(3)
由式(1)、(2)和(3)可得,拉杆拉力:
(4)
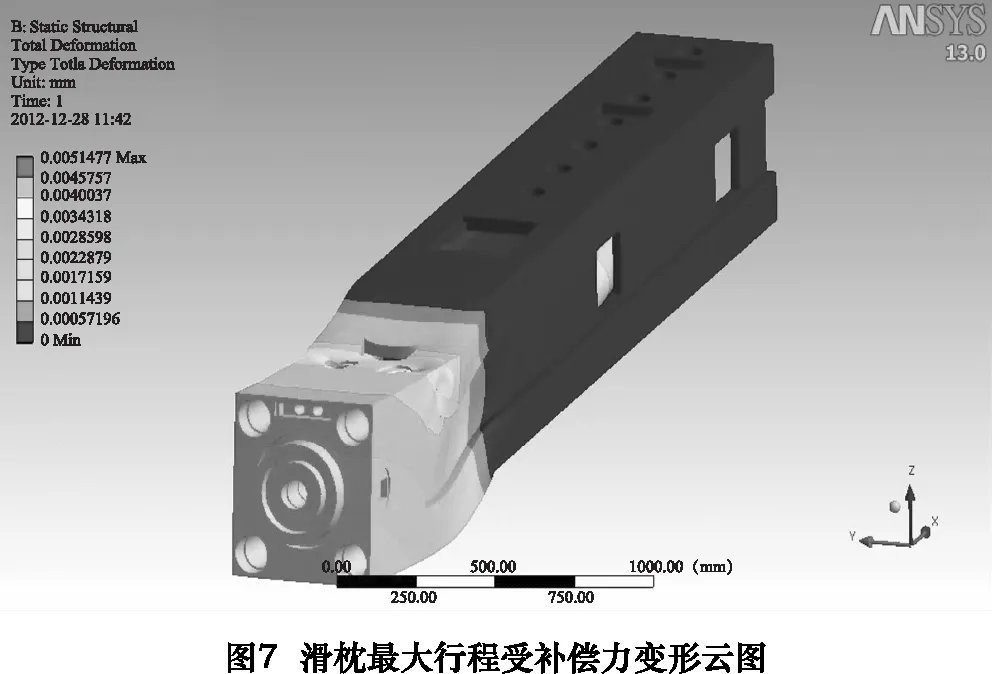
根据式(4)可以求出不同主轴转速下,不同滑枕行程所对应的补偿拉力初算值(F0=11 kN,q=7 kN/m,h=190 mm),并将此初算值施加于有限元模型中,计算出变形量,使滑枕头部挠度满足小于2μm的标准,若不符合,则以此初算值为基础,修改补偿力后再进行有限元分析,直到满足标准为止。分别取主电动机转速为500、1 000和2 000 r/min,计算滑枕行程从800 mm开始,每伸长100 mm所对应的补偿拉力值,并将从ANSYS Workbench中得到的修正值记录于表2中。当机床主轴在n=1 000 r/min的转速下工作时,对滑枕最大行程施加补偿力的变形云图如图7所示。

表2 滑枕行程与拉杆补偿力的关系 kN
多项式最小二乘法能够使曲线拟合误差的平方和最小[9],采用三次多项式最小二乘法分别对表2中3种转速下的数据进行拟合,求出施加在拉杆上的补偿力F与滑枕伸出量l的函数关系式分别为:
当n=500 r/min时,F=-5.8333×10-8l3+1.85×10-4l2-0.1474l+58.71
(5)
当n=1 000 r/min时,F=-4.1667×10-8l3+1.4×10-4l2-0.1161l+48.15
(6)
当n=2 000 r/min时,F=-5×10-8l3+1.6571×10-4l2-0.1459l+56.94
(7)
3种主轴转速下的拉杆拉力F与滑枕伸出量l的拟合曲线如图8所示。
4 结语
(1)在3种不同主轴转速下,利用式(5)~(7)分别计算出滑枕行程l=850、950、1 050及1 150 mm时的拉杆补偿力,输入有限元软件进行计算分析,可得到滑枕头部挠度较小,证明在其他数值点,拟合的光滑曲线与有限元软件计算结果也能较好的吻合。将上述计算值施加在TH6920的滑枕拉杆上,用实验方法测量滑枕头部的挠曲变形,结果显示变形量较小且趋于稳定,能够满足高端数控机床的加工精度要求。

(2)针对TH6920主轴滑枕的挠曲变形及相应的补偿力问题,本文采用的有限元数值拟合方法得到的经验公式具有较高的可信度,利用这种方法可以节省现场调试阶段的实验时间,提高产品生产效率。
[1]舒启林,崔世超,鑫龙.复合式镗铣加工中心滑枕变形分析与补偿研究[J].制造技术与机床, 2014 (12):123-127.
[2]杜平安,于亚婷,刘建涛.有限元法—原理、建模及应用[M].2版.北京:国防工业出版社,2011:143-146.
[3]周震东,王金娥.TH6918滑枕变形分析及补偿方法[J].机械设计与制造,2013 (5):201-203.
[4]孙文才.方滑枕变形处理及补偿的研究[D].哈尔滨:哈尔滨工业大学,2010:9-10.
[5]蔡有杰,王洪才.镗铣床主轴箱重心补偿系统的设计与分析[J].机械设计与制造,2010 (9): 38-39.
[6]Jorgensen B R, Shin Y C. Dynamics of spindle-bearing systems at high speeds including cutting load effects [J]. Journal of Manufacturing Science and Engineering, 1998, 120: 387-394.
[7]Tang Chia-Hui, Chen Tsair-Rong, Chang Ching-Feng. Ram spindle tolerance compensation for horizontal borer [J].The International Journal of Advanced Manufacturing Technology, 2013:1-10.
[8]单辉祖.材料力学[M].北京:高等教育出版社,2009: 202-205.
[9]张光澄.实用数值分析[M].成都:四川大学出版社,2004:128-138.

