基于小波包分析和SVM的透平机振动故障诊断研究
陈庆文,韩景立
(1.中海油(中国)有限公司 天津分公司,天津 300459;2.国网天津市电力公司检修公司,天津 300400)
海上石油平台透平发电机组运行是否良好关系到整个石油平台能否安全生产,因此要求其具有较高的稳定性且运行平稳、噪声达到既定要求[1]。据统计在实际应用中,透平发电机组机械故障中有20%左右的故障均由滚动轴承引起[2],其中包括轴向碰摩、径向碰摩、转子不对中、转子不平衡、轴承内外圈故障、轴承滚动体故障、轴承磨损、轴承保持架故障等[3]。以上故障能够引发透平发电机异常振动,且噪声增大[4]。因此针对透平机的故障诊断意义重大。透平机滚动轴承与很多机械零部件处于同一工作环境,因此当其出现故障时采集的检测信号包含较多噪声[5]。针对透平发电机振动信号为非稳态、噪声较大等特点,本文的处理过程为先用小波包分析对采样信号进行连续小波变换来减小噪声,再运用EMD法分解处理透平发电机产生的振动信号,并将分解后的前7阶IMF分量处理为输入向量运用在SVM中诊断分析透平发电机的故障。本方法在小样本情况亦具有较高的诊断精度。
1 小波包算法
1.1 小波包理论
小波包信号分解即把信号分解并划归到相应的频带[6]。由于每个频带的信号具有相对应的能量,所以可用不同频带中信号的能量组成特征向量来反映设备运行的状态。
1.2 小波包故障特征提取算法
传统小波分析方法仅能对上一次分解所得到的低频部分进行分解,造成高频部分的分辨率较差。小波包分解则利用正交分解,各频带的信号独立,遵守能量守恒定律[7]。其理论依据为Parseval能量积分等式。小波包分析方法中较为常用的算法为Mallat塔式算法,其主要包含分解和重构两方面[8]。
1.2.1 采用低通滤波器和高通滤波器实现信号分解
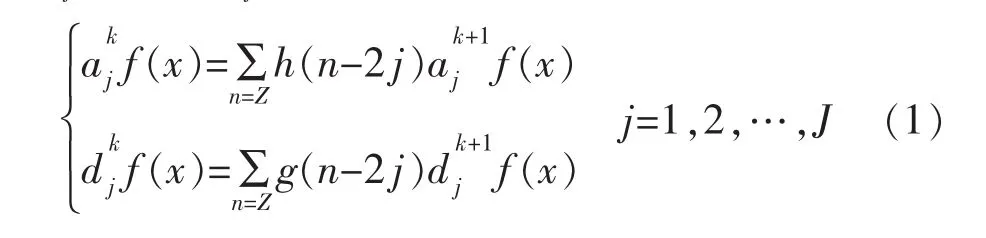
式中:n 为波长;h(n)为低频滤波器系数;g(n)为高通滤波器系数。分解尺度j以及低通滤波系数之间满足:
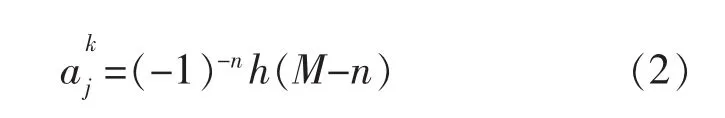
式中:M为滤波器长度;n为波长。
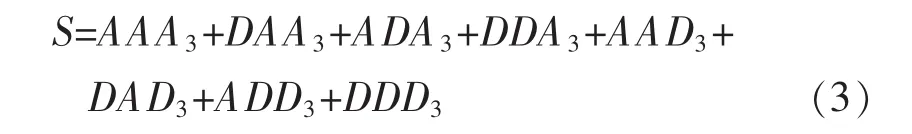
序号数为小波分解的尺度数。随着小波分解的尺度数增大,小波包系数所映射空间分辨率降低。

图1 小波包分解示意Fig.1 Wavelet packet decomposition diagram
1.2.2 信号重构
信号由Mallat塔式分解后得到多层小波系数,再经阈值量化法处理各层小波系数,软限幅函数表示为
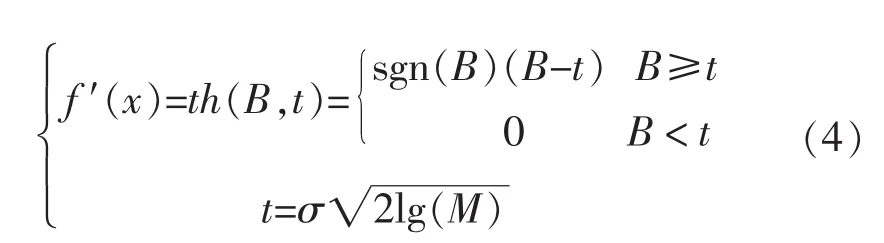
其中t表示软限幅阈值,该式能够实现信号的高频系数重构,得到的重构信号公式为

2 EMD理论
2.1 EMD分解
EMD常用于非线性及非平稳信号处理的时频信号的处理,通过高斯白噪声使信号在不同尺度上连续[9]。EMD分解是把原始信号分解成为许多个能表征模糊频带与瞬时频带的IMF分量,且各IMF分量需满足以下2个条件:
(1)采样信号序列中极大点和极小点数之和与过零点的个数之差小于1;
(2)采样信号局部极大点与极小点确定的频带上下包络线均值为0。
2.2 特征向量提取
设小波包处理降噪后的信号为x(t),选取高频谐波信号 x0(t),将 x0(t)加入到原始信号 x(t)中,分析信号 x′(t)为

找出x′(t)的所有极大值和极小值点,用3次样曲线来连接 x′(t)的上下包络线 u(t)和 l(t)。 上下包络线的平均曲线为
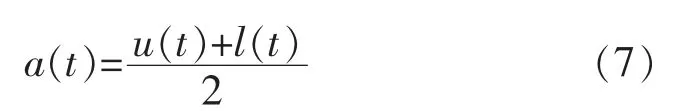
将 x′(t)减去 a(t)可以得到 h(t),若 h(t)与 IMF条件相符合,即可确定 IMF1。 用 x′(t)与 IMF 作差得到余量v,即:

继续判断余量v是否需要继续分解,如不需要,x′(t)表示为

如需要继续分解,则重复式(6)~式(8)继续分解。出现异常信号时故障诊断特征向量可通过IMF1与 x0(t)的差获得[9]。
3 支持向量机
支持向量机是一种基于结构风险最小化原理和统计学习理论上的学习机器,它能够根据有限的样本信息在模型的复杂性与学习能力间寻求最佳效果来获得最优推广能力[10]。支持向量机理论的基本思想是寻找最优分类超平面,在保证分类精度的同时使超平面两侧的空白区域最大化。二维线性可分最优分类线如图2所示。
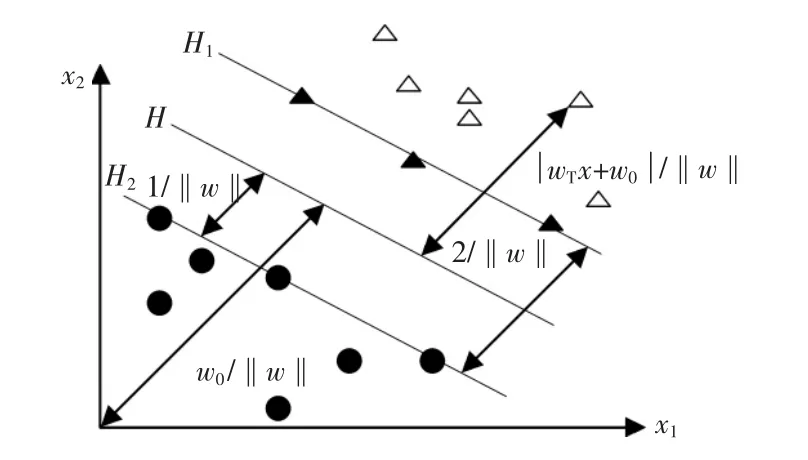
图2 二维线性可分最优分类线Fig.2 Two-dimensional linear separable optimal classification line
设有样本数据集:
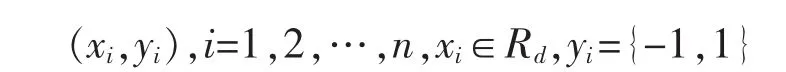
式中:n为训练样本个数;d为每个训练样本向量的维数;yi为分类类别,其值在+1和-1分别为两类,两类样本在图2中分别由圆点和三角形表示。
H为分类超平面,最优超平面可表示为w′x+w0=0,且满足:

式中:w为权重矩阵;w0为阀值。对于超平面H,H1、H2上的样本点即为支持向量。SVM方法中最大化分类间隔2/‖w‖,实际上等价于最小化权重向量的范数‖w‖/2,可用如下带约束条件的优化问题表示:

Φ(ω)是二次型函数,有极小点且唯一,通过拉格朗日乘子法将其转化为对偶形式,此优化问题则转化为对偶问题,
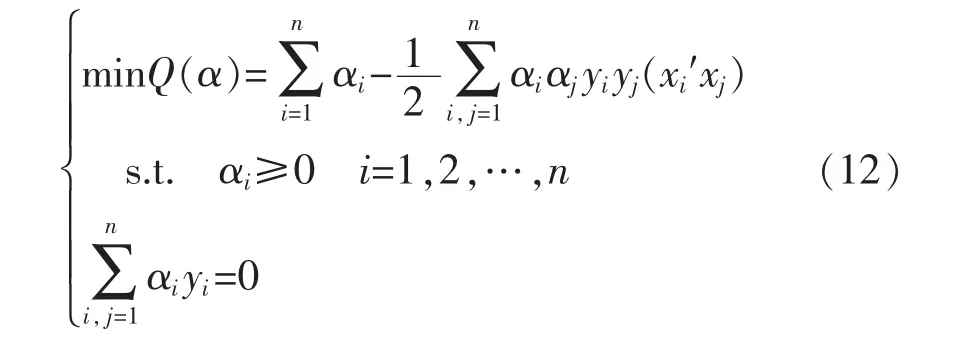
从式(12)可看出,该问题为不等式约束下的二次规划问题,且有唯一解。经过求解,得出最优分类决策函数为
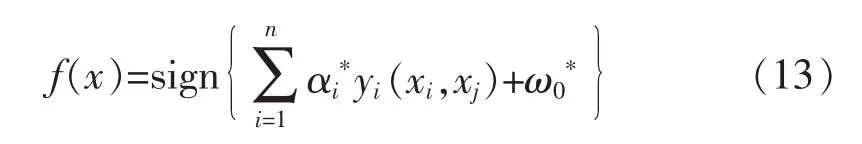
式中:αi*为最优拉格朗日系数;(xi,xj)为满足 Mercer条件的核函数;w0*表示阀值,可由任一支持向量经式(11)取等号求出。
函数式(13)的值域为1或-1,只能作二元区分,当有n种故障类型时,需构造n(n-1)/2个SVM,对各类故障的二分类 SVM分类结果投票,以少数服从多数为原则,将获得票数最多的分类结果作为故障诊断的最终结果。
4 小波包分析与SVM的应用
振动信号数据源自于中海油SZ36-1A平台一台双R透平发电机组,该机组由美国ENTEK振动监测仪采集、处理并将振动数据上传至AB SLC-500 PLC控制系统,经以太网上传给上位机。数据采集系统如图3所示。
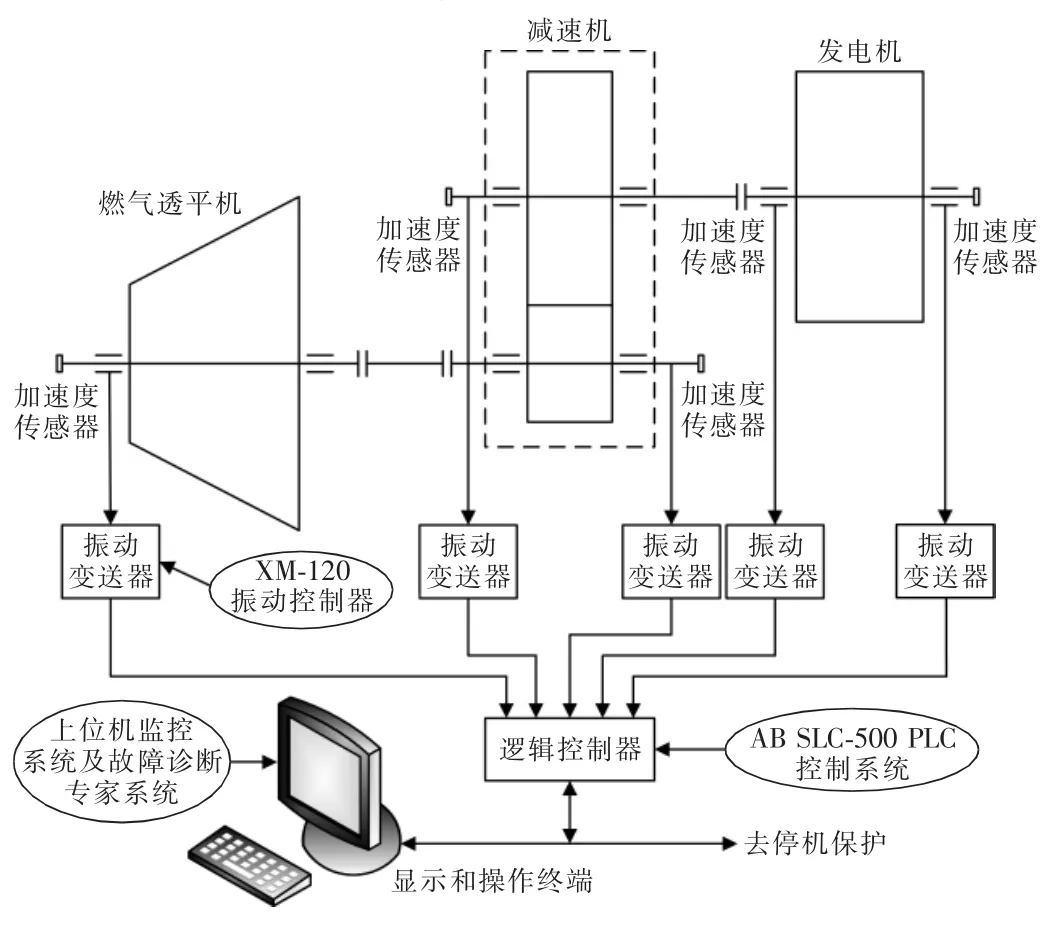
图3 透平发电机数据采集系统Fig.3 Turbine generator data acquisition system
利用上述方法采集燃气透平机5组振动数据,用小波包分解法对数据降噪,并将含有故障信号信息的子频带分量提取出来,将经过小波包降噪的子频带分量进行EMD分解,由此获得IMF分量。原始信号如图4,对小波分解第1层的2个节点进行重构见图5和图6,分别对重构信号进行EMD分解,频率从高到低分解为7个IMF,图7和图8分别为2个重构节点的EMD分解得到的IMF。
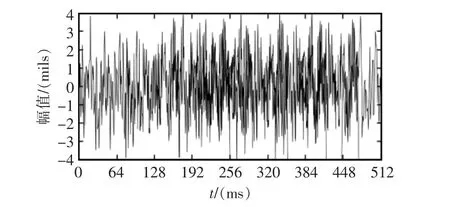
图4 原始信号时域波形Fig.4 Time domain waveform of original signal

图5 重构节点(1,0)Fig.5 Reconstruction node(1,0)
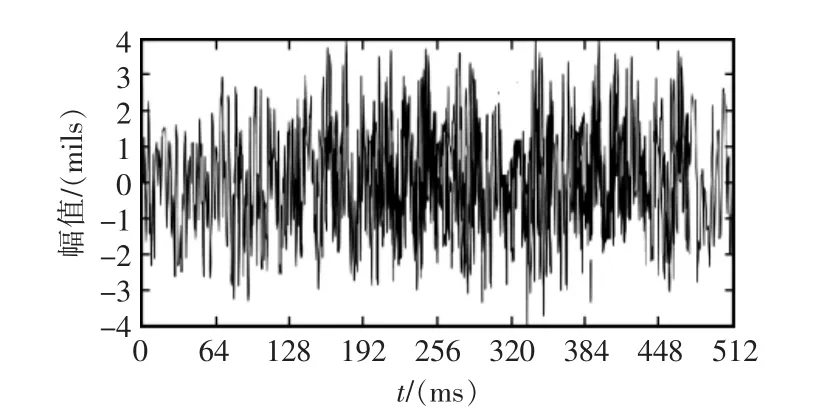
图6 重构节点(1,1)Fig.6 Reconstruction node(1,1)

图7 重构节点(1,0)EMD 分解Fig.7 EMD decomposition of reconstruction node(1,0)

图8 重构节点(1,1)EMD 分解Fig.8 EMD decomposition of reconstruction node(1,1)
根据以往经验,故障信息大多存在于前几个IMF分量,因此本试验选取前7个IMF分量组成故障诊断向量,并将故障诊断向量作归一化处理。部分训练样本数据见表1。

表1 透平发电机提取的故障诊断特征向量Tab.1 Fault diagnosis feature vector extracted by turbine generator
将表中的特征向量作为支持向量机的输入向量,并以此训练6种二分类支持向量机的振动故障诊断模型,使用高斯径向基核函数,确定均值u=0.5,方差 σ=0.95。
表2显示的数据为故障诊断结果。由表2可以得出4种故障的诊断精度皆大于90.00%,最高诊断精度为96.00%,总数据类别诊断精度为94.00%,可见此方法的诊断精度较高。
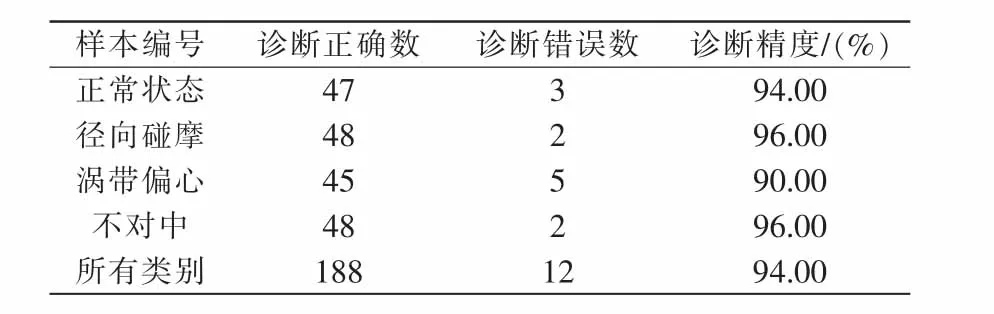
表2 振动故障诊断结果Tab.2 Vibration fault diagnosis result
5 结语
本文提出基于小波包分析和SVM的透平机振动故障分类器,将振动信号进行小波包分解并重构进行降噪,在降噪后的故障子频带信号基础上采用EMD方法获得故障诊断特征向量,输入到支持向量机构成的多故障分类器中进行故障识别和分类。该分类器需要的训练样本少,故障诊断精度较高。结果表明该方法具有较强的有效性和实用性,应用前景良好。
[1]胡子谷,宓为建,石来德.故障振动信号的小波包分解与诊断[J].振动与冲击,1998(2):57-62.
[2]赵志宏,杨绍普.基于小波包变换与样本熵的滚动轴承故障诊断[J].振动、测试与诊断,2012,32(4):640-644.
[3]叶瑞召,李万红.基于小波包分解和BP神经网络的轴承故障诊断[J].轴承,2012(10):53-56.
[4]黄中华,尹泽勇,刘少军,等.基于小波包分解的滚动轴承故障诊断[J].湖南科技大学学报:自然科学版,2008,23(2):32-35.
[5]宋友,柳重堪,李其汉.基于小波包分解的早期碰摩故障诊断研究[J].北京航空航天大学学报,2003,29(1):87-90.
[6]杨保海,陈栋,郑冬喜,等.基于小波包分解和EMD-SVM的轴承故障诊断方法[J].计算机测量与控制,2015,23(4):1118-1120.
[7]吕永卫,熊诗波,林选,等.基于小波包和EMD处理的滚动轴承故障诊断[J].太原理工大学学报,2010,41(2):178-182.
[8]何学文,卜英勇.基于小波包分解和支持向量机的机械故障诊断方法[J].机械强度,2004,26(1):20-24.
[9]李自国.基于支持向量数据描述的故障诊断方法研究[D].郑州:郑州大学,2007.
[10]付华,尹丽娜.小波包分解在电机故障诊断中的应用[J].微电机,2007,40(5):86-89.

